基于蒙特卡洛方法的液压泵变量伺服机构稳健性优化

汪浒江，毛明，唐守生，冀海

(中国北方车辆研究所 车辆传动重点实验室，北京100072)

0 引言

液压泵变量伺服机构是一个典型的机械液压位置伺服系统，此类机构广泛应用于飞机、导弹、仿形机床等领域［1］。当其应用于履带车辆静液转向操纵时，控制系统的跟踪精度及稳健性非常重要。履带车辆使用条件恶劣，实际系统工作时存在许多显著的不确定性因素，如不稳定的伺服控制油压、不确定的液压油泄漏量、驾驶员操纵机构中机械零件的变形、磨损、装配间隙以及转向负载的动态变化等，因此需要特别关注液压泵变量伺服机构在面对显著不确定性因素时，系统的工作性能能否保证稳定，即保证系统性能的稳健性。

针对液压泵变量伺服机构在动态特性建模分析与仿真、系统参数优化等方面，研究人员均已做过大量的工作［2-6］，而关于如何考虑伺服机构中的不确定性因素，研究系统性能的稳健性及其优化问题，尚未见到相关文献资料。

稳健性优化设计思想源自日本田口在20 世纪二战之后提出的产品质量管理思想，其基本思想是，在不消除和不减小不确定性源的前提下，通过对可控因素的合理匹配并控制其容差，降低产品在设计点上的敏感性，控制并减小目标函数的波动，以实现产品质量特性“均值趋于最优”、“均方差趋于最小”的目的［7-8］。

本文利用蒙特卡洛方法建立了适用于液压泵变量伺服机构的稳健性优化设计新方法。根据履带车辆对静液转向控制机构的特殊需求，以系统性能的稳健性为优化目标，以系统关键结构参数名义值为设计变量，利用模拟退火算法实现优化问题的求解，并给出具体的应用实例。

1 工作原理

图1为液压泵变量伺服机构的结构示意图，其由三位四通转阀、双作用液压缸、活塞、反馈拨叉、对中装置、操纵连杆机构等组成，其中，转阀用于控制油液的流量和方向，活塞用于驱动斜盘克服负载摆动一定角度，实现柱塞泵排量变化，反馈拨叉用于实现外部反馈。图2为液压泵变量伺服机构的工作原理图。转阀中，P 为进油口，T 为回油口，A、B 为工作油口，M、G 为柱塞泵进、出油口。初始状态时，液压缸中活塞处于中位，转阀处于中位。当驾驶员操纵车辆转向时，操纵连杆机构动作，带动阀芯动作，转阀随之开启。此时若转向信号使转阀左位接通，则P 口与A 口接通，B 口与T 口接通，压力油液进入液压缸左腔推动活塞向右移动。反馈拨叉实时感知活塞位移并反馈给转阀阀套，并促使转阀关闭，活塞随之停止运动。由此可见，当驾驶员转向操纵信号(方向盘转角)为一定值时，转阀阀芯输入角度就为一确定量，进入稳定状态后活塞的位移也将是一确定量。活塞推动斜盘转动，进而调节柱塞泵的排量，由此实现对履带车辆转向半径的稳定控制。液压泵变量伺服机构作为履带车辆转向的控制机构，其必须具有足够的稳定性以保证转向的可控性和平稳性，必须具有足够的跟踪精度以保证转向过程的准确性。在该系统中，阀芯的转角控制信号θi为系统的输入，活塞的位移y 为系统的输出。

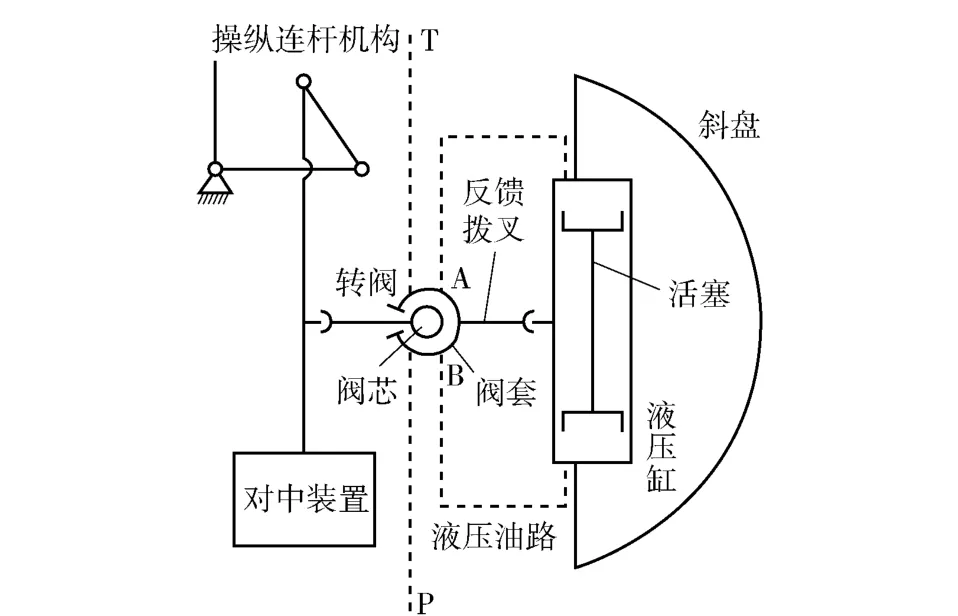
图1 变量伺服机构结构示意图Fig.1 Structure diagram of stroking mechanism

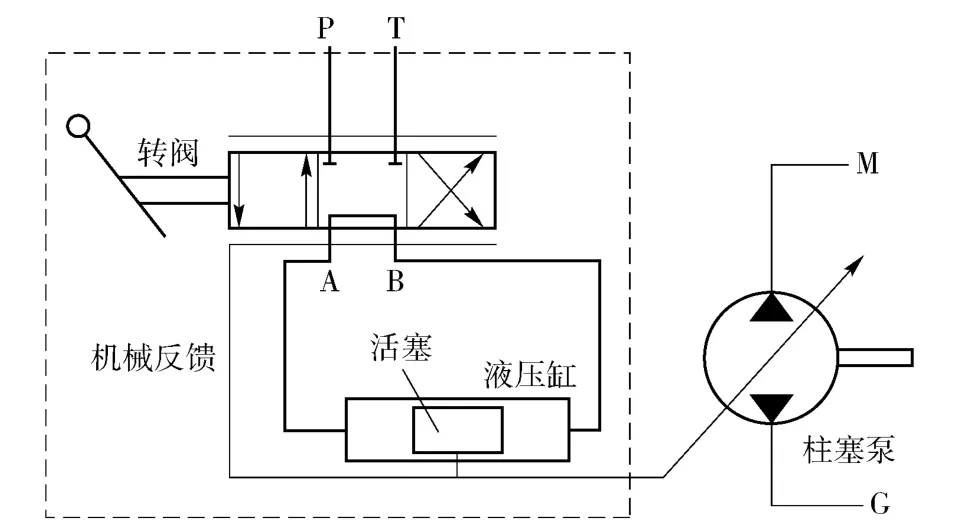
图2 变量伺服机构工作原理图Fig.2 Schematic diagram of stroking mechanism

2 动力学模型

根据工程流体力学相关理论［9］，具有匹配、对称节流阀口的理想零开口阀的压力-流量特性方程为

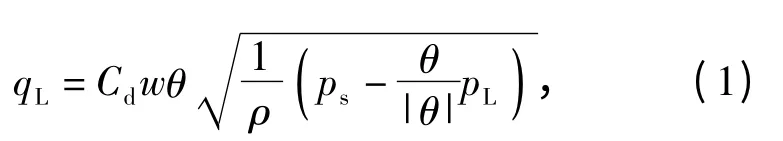
式中:qL为负载流量(m3/s);w 为阀口梯度(转阀节流口的过流面积对其开口角度的变化率(m2/rad));θ 为转阀开口角度(rad);ρ 为油液密度(kg/m3);ps为伺服控制油压(Pa);pL为负载压降(液压缸两腔油液压力之差，Pa);Cd为流量系数，其是一个常值，转阀节流口可视为薄壁孔口，根据文献［10］，其值可取0.62.

液压缸的流量连续性方程［9］为

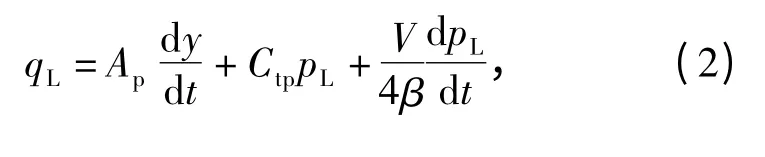
式中:Ap为活塞面积(m2);y 为活塞位移(m);Ctp为液压缸总泄漏系数(m3/(s·Pa));V 为总压缩体积(转阀与液压缸间油道及液压缸两腔的油液总体积，m3);β 为油液有效体积弹性模量，通常，如果没有β 的实测值，计算时其值可取在700 ～1 200 MPa之间［9］。

(2)式中:等号右边第1 项为推动活塞运动所需流量;第2 项为总泄漏流量;第3 项为总压缩流量(由于转阀与液压缸间油道及液压缸两腔的油液压缩变形而引起的流量)。

液压缸和负载的力平衡方程为

式中:m 为等效负载质量(kg);B 为等效负载阻尼系数(N·s/m);F 为活塞上受到的任意外负载力(N).

反馈拨叉将活塞的位移y 变换成转阀阀套的转角θf，如果不考虑结构的变形和间隙误差，有

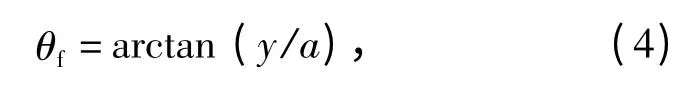
式中:θf的单位是rad;a 为反馈拨叉长度(m).

驾驶员操纵方向盘的动作通过操纵连杆机构作用于阀芯，而反馈拨叉作用于阀套，阀芯与阀套的相互关系确定了转阀阀口的实际开口角度θ.

式中:θi为方向盘转角信号通过操纵连杆机构作用于阀芯的输入角度(rad)。

(1)式～(5)式描述了液压泵变量伺服机构的动态工作特性，其中(1)式考虑了流量与压力间的非线性关系，(2)式考虑了油液的压缩和泄漏，(4)式考虑了反馈结构的非线性特性。(1)式～(5)式比较精确地描述了系统输入θi、输出y、负载F 间的动态关系。根据(1)式～(5)式利用MATLAB 建立变量伺服机构仿真模型。

3 评价指标

3.1 系统的跟踪精度

系统的跟踪精度IAE 定义为误差绝对值的积分［11］。

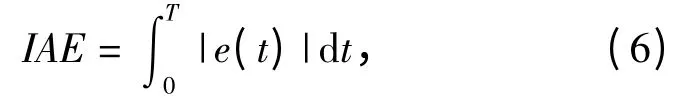
式中:e(t)为系统的误差，它定义为系统输出量的期望值与实际值之差，它是一个时间的函数;T 为累计误差时长。

对于一个控制系统，系统的误差e(t)主要由系统参数、输入信号和负载决定［12］。从设计的角度讲，最关心通过合理匹配系统参数以减小系统误差，因此在分析之前，需要定义清楚系统的输入信号及负载形式。在文献［3，5］中，相关学者曾将液压泵变量伺服机构所受外负载力简化考虑为一个恒值力。此处，用伺服机构克服恒值外负载力，对目标信号θ*=ymaxsin(2πt)的累积跟踪误差IAE 来评价系统的跟踪精度。此时，控制指令信号应为

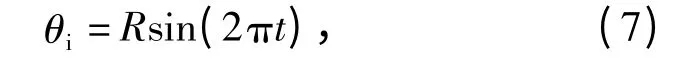
式中:R=arctan(ymax/a)，ymax为活塞行程的一半。

图3给出了仿真获取的某一液压泵变量伺服机构实际响应与目标信号之间的关系。由图3可以看出，活塞的位置响应完全跟随目标信号而变化，其跟踪误差可能为正，也可能为负。此跟踪误差直接体现在履带车辆转向轨迹的可控性上，过大的跟踪误差导致的转向超前与滞后均不利于驾驶员对车辆的操纵。

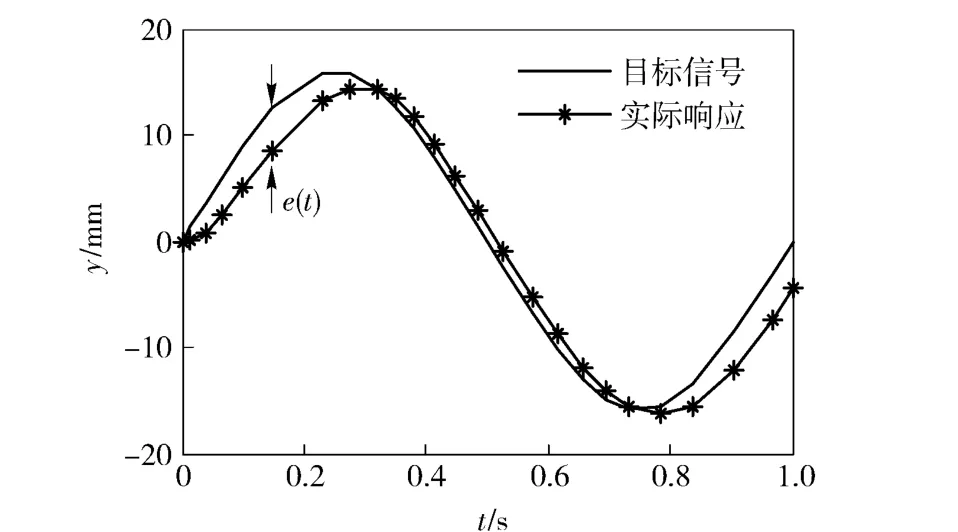
图3 变量伺服机构的跟踪误差e(t)Fig.3 Target signal and actual response of stroking mechanism

3.2 幅值裕量

稳定性是一个系统可控的先决条件。零位幅值裕量可用于评价液压泵变量伺服机构相对稳定性的大小，其值为正，则系统稳定，其值越大，则系统相对稳定性越好。幅值裕量Kg计算公式［9］为

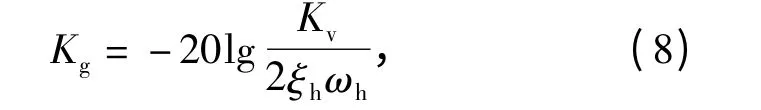
式中:ωh为系统的液压固有频率;ξh为系统零位下的阻尼比，通常取值0.1 ～0.2;Kv为系统的开环增益。

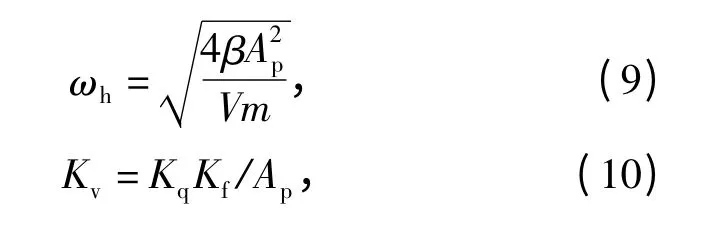
式中:Kq为转阀的流量增益;Kf为反馈增益。理想零开口阀零位下的流量增益为

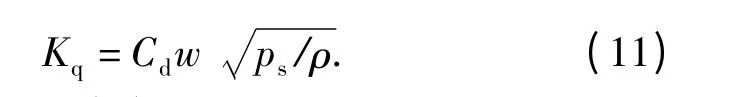
反馈增益Kf由(4)式在y =0 处利用泰勒级数展开，忽略高阶无穷小项得到:

根据(8)式～(12)式，推导得液压泵变量伺服机构零位下的幅值裕量为

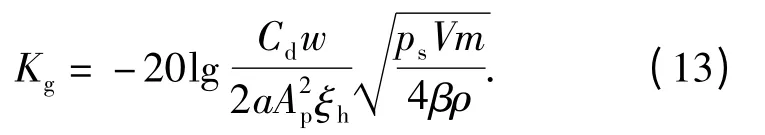
4 蒙特卡洛模型

蒙特卡洛方法是一种以概率统计理论为基础的计算机随机模拟方法，二战末为解决核武器研制过程中遇到的中子扩散问题而首次提出。作为当前比较成熟的一种不确定性分析方法，非常适用于非线性系统的分析［13-14］。

从设计的角度，影响产品质量特性的因素可分为两类:一类是设计过程中易于控制的参数，如产品的几何尺寸，称可控因素;另一类是设计过程中不易控制的参数，如泄漏量、工作环境参数等，称噪声因子。变量伺服机构中反馈拨叉长度a、阀口梯度w、活塞直径D、伺服控制油压ps、总泄漏系数Ctp直接决定系统的稳定性及跟踪精度，是系统质量特性的关键影响因素。其中，a、w、D 为结构参数，在设计过程中易于通过调整其设计名义尺寸加以控制，为可控因素。伺服控制油压ps、总泄漏系数Ctp在设计过程中不易保证，为噪声因子。结构参数由于加工误差，使用过程中的磨损、变形，具有不确定性。伺服控制油压、总泄漏系数存在波动，也具有不确定性。这些不确定性可以利用概率密度分布函数来描述。参数的不确定性进一步导致系统性能的波动，现代稳健性设计思想即追求在设计阶段通过对可控因素的合理匹配，抑制噪声因子在使用过程中对产品质量特性的影响，并减小产品质量特性在设计点处的敏感度。

综合考虑存在不稳定的伺服控制油压、不确定的泄漏量以及由于加工误差、磨损、变形等导致结构参数实际值相对名义值的波动，利用图4所示蒙特卡洛模拟流程图可获取某一设计参数组合［a*w*D*］下系统性能指标的均值和标准差。

根据图4所示流程图在MATLAB 中建立蒙特卡洛模型。其中，a*、w*、D*分别为反馈拨叉长度、阀口梯度、活塞直径的设计名义值，是蒙特卡洛模型的输入;a(i)、w(i)、D(i)、ps(i)、Ctp(i)(i =1，2，…，N)分别为反馈拨叉长度、阀口梯度、活塞直径、伺服控制油压、总流量泄漏系数实际值的模拟值，其服从所定义的概率分布，是蒙特卡洛模型的中间状态量;IAE、Kg的均值、标准差通过对某一设计参数组合下IAE、Kg的响应面统计分析获取，为蒙特卡洛模型的输出。

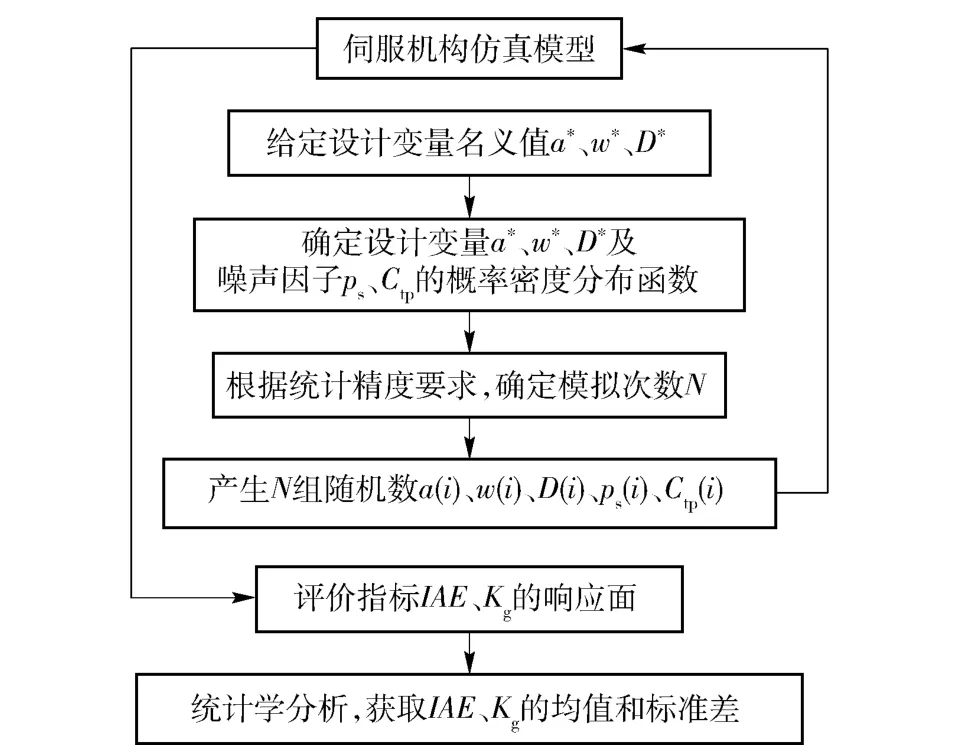
图4 蒙特卡洛模拟流程图Fig.4 Flow chat of Monte Carlo simulation

5 稳健性优化

传统设计中，为了控制产品质量特性的波动，通常采取减小影响因素容差来实现，此以增加制造和使用成本为代价。实际上，对于一个复杂的系统，产品的质量特性与影响因素之间通常存在复杂的非线性特性。稳健性设计正是要合理利用这种非线性关系，力图将设计点确定在产品质量特性的低敏感区。此种设计方法，在提升产品性能并减小其性能波动的同时，并不增加成本。

此处建立液压泵变量伺服机构的稳健性优化设计模型，试图在不苛刻工艺及使用条件的情况下，即结构参数及噪声因子变动范围均不变的情况下，通过优化匹配关键结构参数的设计名义值，达到以下两点设计效果:1)提升产品性能，使跟踪精度、稳定性指标“均值趋于最优”;2)提升变量伺服机构抵抗结构参数、伺服控制油压以及总油液泄漏量变动的能力，即使跟踪精度、稳定性指标“均方差趋于最小”。

通过前面的研究可以看出，系统的优化目标是系统的跟踪精度最优、稳定性最优，并保持系统性能的稳健性最优。因此有IAE 均值最小、Kg均值最大，且IAE、Kg标准差最小。则其目标函数表达式为

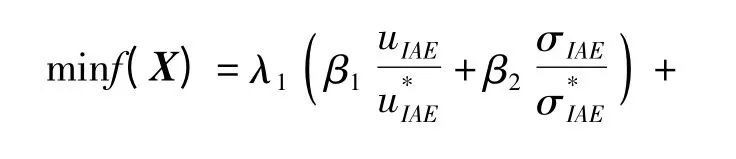
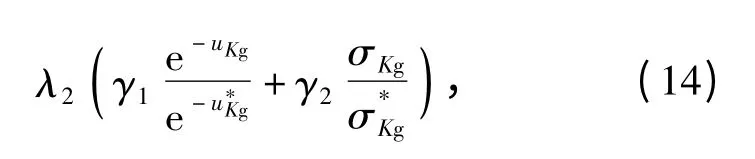
式中:uIAE、σIAE、uKg、σKg分别为某一设计参数组合(a*w*D*)下性能指标IAE、Kg的均值和标准差;λ1、λ2、β1、β2、γ1、γ2为加权系数，分别为优化前系统性能指标IAE、Kg的均值和标准差，其对待优化项进行归一化处理，以消除优化过程中uIAE、σIAE、uKg、σKg数量级差异对目标函数的影响。

以液压泵变量伺服机构的关键结构参数反馈拨叉长度、阀口梯度、活塞直径的设计名义值为优化变量，即:

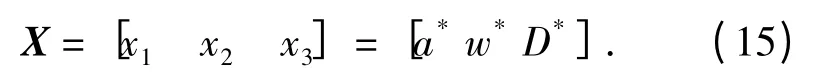
以上关键结构参数受总体结构尺寸的限制，即设计变量名义值必须在一定范围内选择，即

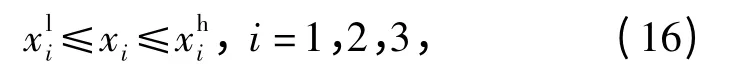
式中:xli、xhi分别为反馈拨叉长度、阀口梯度、活塞直径名义值的上、下限。

上述优化模型可选择模拟退火算法进行求解。

6 实例

6.1 实例参数

某液压泵变量伺服机构，系统参数如表1所示。

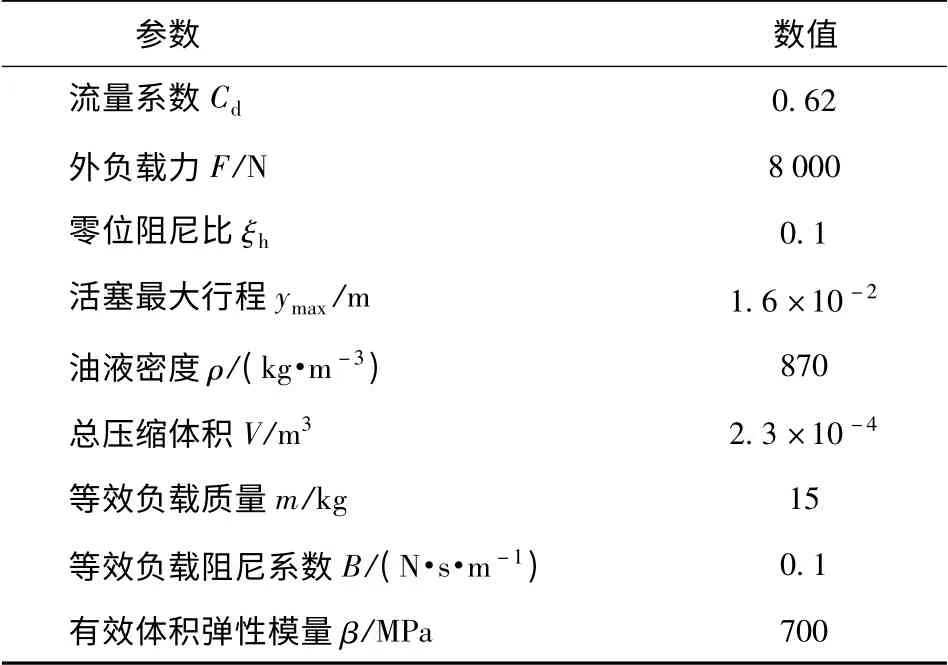
表1 变量伺服机构系统参数Tab.1 System parameters of stroking mechanism

6.2 稳健优化模型参数

反馈拨叉长度、阀口梯度、活塞直径名义尺寸的上、下限分别为:x1∈［22 mm 51 mm］;x2∈［35 mm2/rad 90 mm2/rad］;x3∈［28 mm 70 mm］.IAE 累计误差时长取一个正弦周期。视各优化子项同等重要，故各加权系数均取值0.5.

6.3 设计变量及噪声因子概率分布

该实例中，反馈拨叉长度近似服从a ～N(a*，0.332)，单位mm;阀口梯度近似服从w ～N(w*，3.32)，单位mm2/rad;活塞直径近似服从D ～N(D*，0.332)，单位mm;总泄漏系数近似服从Ctp～N(8.5 ×10-12，(1.7 ×10-12)2)，单位m3/(s·Pa);伺服控制油压近似服从ps～N(5，0.52)，单位MPa.以上所用各参数概率分布，是作者基于经验而做出的基本假设，有其局限性，更准确的概率分布依赖于进一步的试验研究及数据统计，但并不影响本文述及的理论和方法。

6.4 优化结果

蒙特卡洛模拟次数取100，选择模拟退火算法完成优化，优化前后结果对比如表2所示。

表2 稳健性优化前后关键结构参数对比Tab.2 Key structure parameters before and after optimization

6.5 稳健性分析

分别对优化前、后结果应用蒙特卡洛模拟进行稳健性分析，蒙特卡洛随机采样次数N 取5 000，优化前、后各性能指标对比如表3所示。

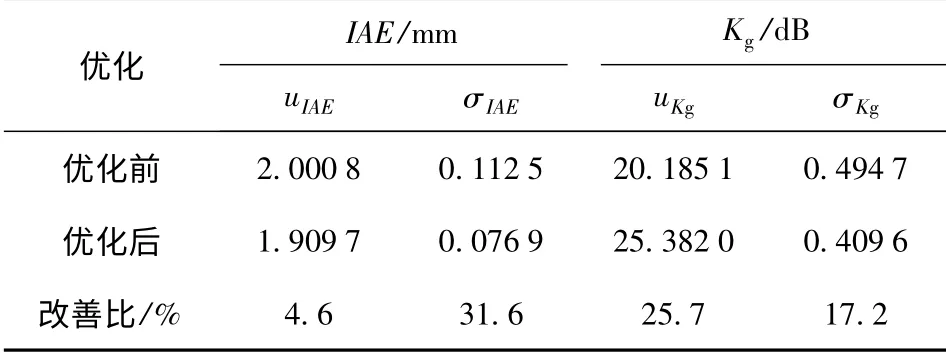
表3 稳健性优化前后各性能指标对比Tab.3 Performance indexes before and after optimization

直方图组数取100，优化前、后IAE、Kg响应面模型概率分布直方图如图5～图8所示。

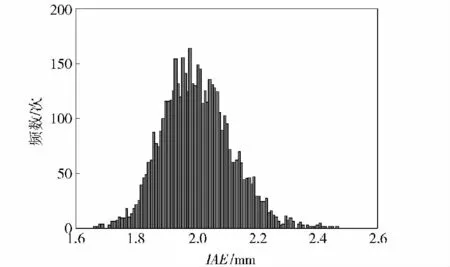
图5 优化前IAE 响应面概率分布Fig.5 Response surface of IAE before optimization

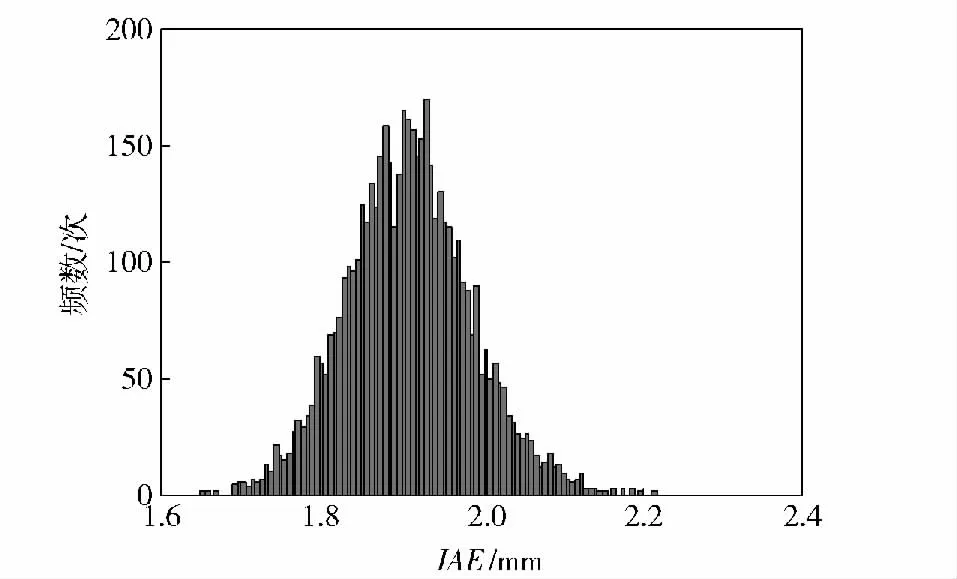
图6 优化后IAE 响应面概率分布Fig.6 Response surface of IAE after optimization

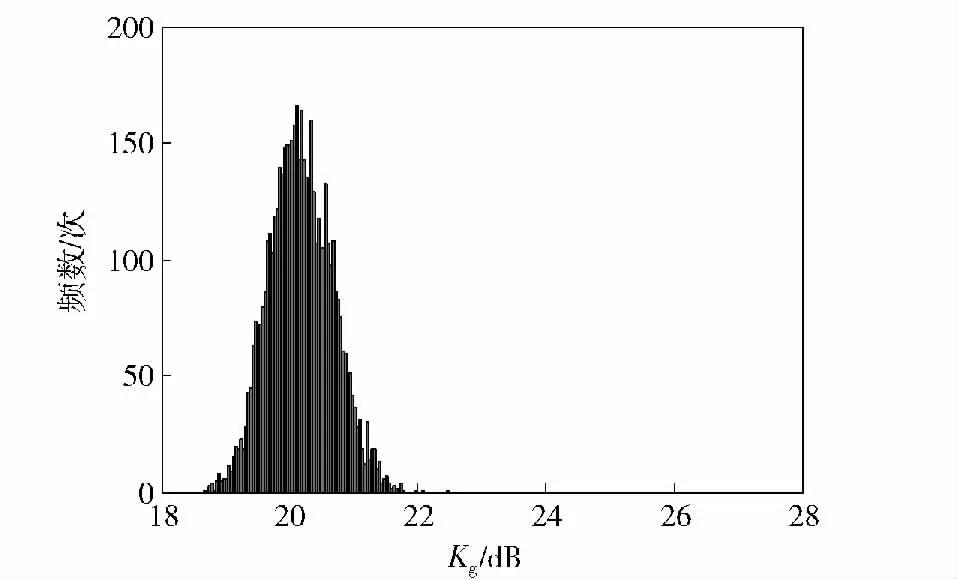
图7 优化前Kg响应面概率分布Fig.7 Response surface of Kg before optimization

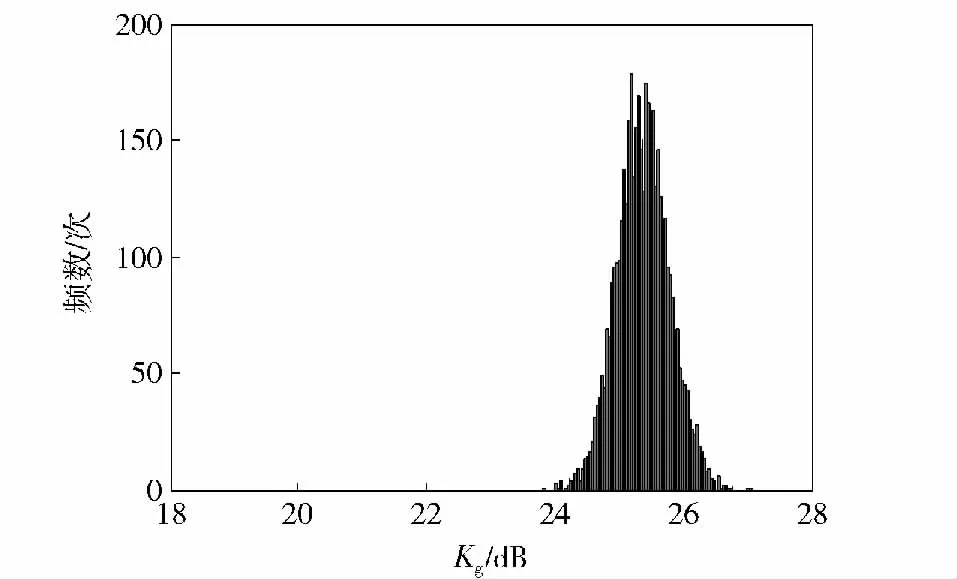
图8 优化后Kg响应面概率分布Fig.8 Response surface of Kg after optimization

对仿真结果进行正态分布拟合，图9、图10 分别为IAE、Kg优化前后的概率密度分布函数对比图。

从图5～图10 可以看出，经过稳健性优化，变量伺服机构跟踪精度IAE“均值趋于最小，均方差趋于最小”，零位幅值裕量Kg“均值趋于最大，均方差趋于最大”，表明经过稳健性优化，不仅保证系统具备良好的跟踪精度及相对稳定性，而且显著提升了系统抵抗结构参数、油液参数变动的能力，系统在恶劣环境下稳定工作的能力显著增强，稳健性优化效果显著。

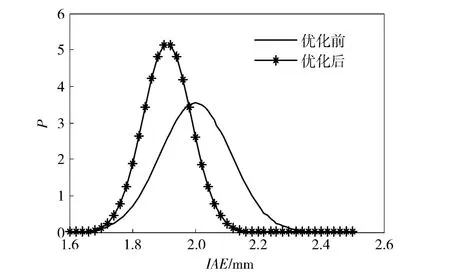
图9 优化前后IAE 概率密度分布函数Fig.9 Probability density functions of IAE before and after optimization

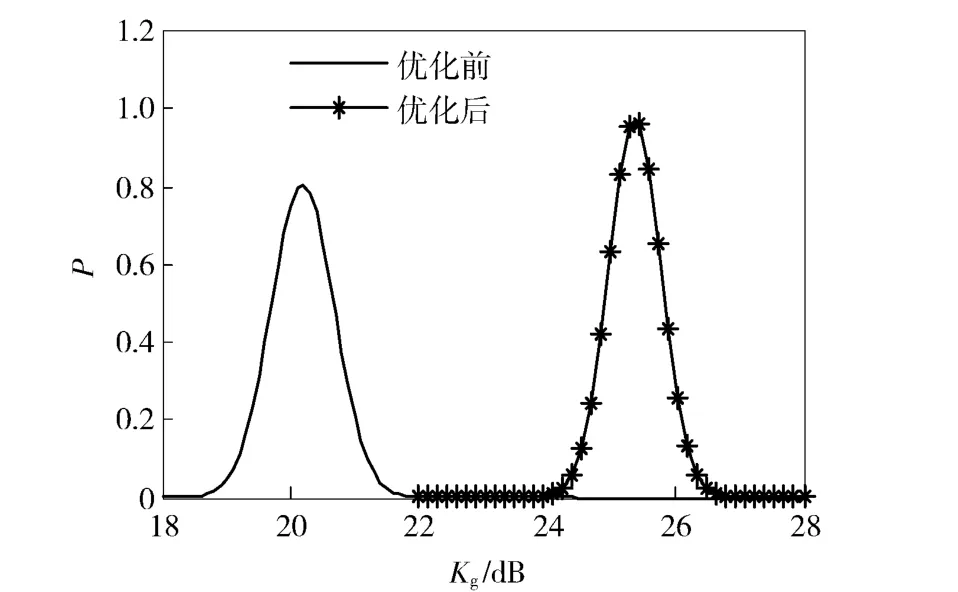
图10 优化前后Kg概率密度分布函数Fig.10 Probability density functions of Kg before and after optimization

7 结论

本文针对履带车辆对静液转向操纵机构性能及稳健性的特殊需求，提出了变量伺服机构稳健性设计新方法。以系统动态跟踪精度、相对稳定性性能指标分布的均值及标准差为优化目标，以反馈拨叉长度、阀口梯度、活塞直径的设计名义值为优化变量，利用蒙特卡洛方法构建液压泵变量伺服机构的稳健性优化设计模型，利用模拟退火算法实现优化问题的求解。

通过应用案例可以看出，稳健性优化效果显著。在相同结构参数及噪声因子波动水平下，通过优化匹配反馈拨叉长度、阀口梯度、活塞直径的设计名义值，系统的跟踪精度及相对稳定性大幅提升，稳健性大幅提升。表明所提出的稳健性优化设计新方法在不增加制造工艺，不减小环境干扰的情况下，通过选取关键参数并进行优化匹配设计，不仅能提升变量伺服机构各项性能，而且显著增强了系统抵抗结构参数、油液参数变动的能力，此设计方法对获得“低成本、高性能、高恶劣环境耐受度”的装备具有参考意义。

References)

［1］张利平. 液压控制系统及设计［M］. 北京:化学工业出版社，2007.ZHANG Li-ping. Control and design of hydraulic control system［M］.Beijing:Chemical Industry Press，2007. (in Chinese)

［2］郭杰，刘广瑞.轴向柱塞泵变量机构的数学建模及控制系统仿真分析［J］.机床与液压，2013，41(3):106 -109.GUO Jie，LIU Guang-rui. Mathematical modeling of the stroking mechanism of axial piston pump and its control system simulation analysis［J］. Machine Tool &Hydraulics，2013，41(3):106 -109. (in Chinese)

［3］焦宗夏，王占林. 变量机构主要参数的优化设计［J］. 机床与液压，1993，21(6):339 -342.JIAO Zong-xia，WANG Zhan-lin. The optimization of the stroking mechanism main parameters ［J］. Machine Tool &Hydraulics，1993，21(6):339 -342. (in Chinese)

［4］宋俊. 轴向柱塞泵变量机构功率匹配优化设计［J］. 机械设计与制造，2000(3):50 -51.SONG Jun. The optimization of axial piston pump stroking mechanism by matching power［J］. Machinery Design ＆ Manufacture，2000(3):50 -51. (in Chinese)

［5］李泽松，寇子明. A4VG 系列变量泵伺服机构动态特性分析［J］.煤矿机电，2005(2):8 -9，12.LI Ze-song，KOU Zi-ming. Servo dynamics analysis of A4VG series variable displacement pumps［J］. Colliery Mechanical ＆ Electrical Technology，2005(2):8 -9，12. (in Chinese)

［6］李磊，许明恒，于兰英，等. 位移-力反馈型变量机构理论建模与试验研究［J］.机械科学与技术，2012，31(4):578 -582.LI Lei，XU Ming-heng，YU Lan-ying，et al. Theoretical modeling and experimental research on variable-displacement mechanism with displacement-force-feedback［J］. Mechanical Science and Technology for Aerospace Engineering，2012，31(4):578 -582.(in Chinese)

［7］郑健，成艾国，董立强，等.田口鲁棒设计方法在汽车耐撞性优化中的应用［J］.汽车工程，2011，33(9):772 -776.ZHENG Jian，CHENG Ai-guo，DONG Li-qiang，et al. The application of Taguchi robust design to vehicle crashworthiness optimization［J］. Automotive Engineering，2011，33(9):772 -776. (in Chinese)

［8］李玉强，崔振山，阮雪榆，等. 6σ 概率优化设计方法及其应用［J］.中国机械工程，2004，15(21):1916 -1919.LI Yu-qiang，CUI Zhen-shan，RUAN Xue-yu，et al. 6σ based probabilistic design optimization method and applications［J］. China Mechanical Engineering，2004，15(21):1916 -1919. (in Chinese)

［9］王春行. 液压控制系统［M］. 北京:机械工业出版社，1995.WANG Chun-xing. Hydraulic control system［M］. Beijing:China Mechine Press，1995. (in Chinese)

［10］张也影. 流体力学［M］. 北京:高等教育出版社，1999.ZHANG Ye-ying. Fluid mechanics［M］. Beijing:Higher Education Press，1999. (in Chinese)

［11］Richard C D，Robert H B. 现代控制系统［M］. 谢红卫，邹蓬兴，张明，等，译. 北京:高等教育出版社，2001.Richard C D，Robert H B. Modern control system［M］. XIE Hong-wei，ZOU Peng-xing，ZHANG-Ming，et al，translated.Beijing:Higher Education Press，2001. (in Chinese)

［12］陈康宁. 机械工程控制基础［M］. 西安:西安交通大学出版社，1997.CHEN Kang-ning. The control basis of mechanical engineering［M］.Xi’an:Xi’an Jiaotong University Press，1997. (in Chinese)

［13］朱辉，刘义保，游运，等. 蒙特卡罗方法与拟蒙特卡罗方法的历史、现状及展望［J］. 东华理工大学学报:自然科学版，2010，33(4):357 -362.ZHU Hui，LIU Yi-bao，YOU Yun，et al. Monte Carlo method and quasi-Monte Carlo method［J］. Journal of East China Institute of Technology:Natural Science，2010，33(4):357 -362.(in Chinese)

［14］张超，陈磊，陈宗基，等. 基于视觉的UCAV 自主着陆蒙特卡洛仿真研究［J］.系统仿真学报，2010，22(9):2235 -2240.ZHANG Chao，CHEN Lei，CHEN Zong-ji，et al. Monte Corlo simulation for vision-based autonomous landing of unmanned combat aerial vehicles ［J］. Journal of System Simulation，2010，22(9):2235 -2240. (in Chinese)