高压弹射装置内弹道二维模型及发射腔内流场特性分析

蒋淑园，王浩，阮文俊

(南京理工大学 能源与动力工程学院，江苏 南京210094)

0 引言

高压弹射装置［1］在武器发射领域［2-3］具有广泛的应用。其组成如图1所示［4］，由点火头、药室、燃气室、弹丸、发射腔等元件组成。当接到发射指令后，点火击发机构点燃火药，火药迅速点火燃烧，积聚产生高压气体，在一定压力时，解锁弹丸，弹丸被赋予一定的弹射速度，由弹射装置内抛出。火药在药室内点燃至弹丸启动这段时间内，火药气体积聚成高压，积聚的高压气体在弹丸被解锁后瞬时释放，这一内弹道过程中，高压弹射装置长径比小，药室容积变化快等结构上的特点，意味着流场的复杂变化，而流场分布情况将直接影响弹丸弹射姿态的稳定与弹射速度的大小等。为了掌握这一阶段发射腔内的流场情况，本文将对所研究的高压弹射装置建立内弹道二维模型［5］，编制程序进行数值模拟，将计算结果与试验结果进行对比，同时通过对发射腔内压力、气体速度等特征参量沿轴向和径向分布情况的分析，掌握发射腔内气体流动变化规律，得到高压弹射装置的流场特性，为下一步研究工作奠定基础。

1 数学物理模型

1.1 数学模型

高压弹射装置结构如图1所示。点火头击发点火，火药在药室内燃烧，达到药室破孔压力后，火药气体从喷孔喷出，进入燃气室。当燃气压力达到弹丸启动压力时，推板打开，推动弹丸一起运动至出炮口。

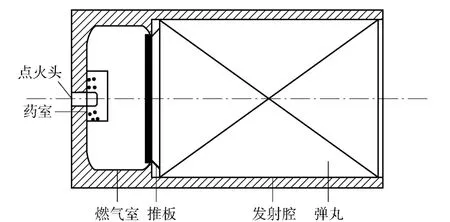
图1 发射系统结构示意图Fig.1 Structure diagram of launching system

1.2 基本假设

1)火药燃烧模型。火药的燃烧满足几何燃烧定律的条件，火药的燃烧速度定律为燃烧室内平均压力的指数函数;点火药瞬间燃完，并形成主装药的点火压力。

2)火药燃气模型。火药燃气服从诺贝尔方程，且火药力、余容、比热比等为常数;喷孔瞬时打开，喷孔的膜片同时破裂，燃气流动为等熵流动。

3)弹丸运动模型。燃气室内压力达到弹带挤进压力后，弹丸瞬间解除约束并开始运动;且弹丸运动为轴向一维运动，所受运动阻力用虚拟质量系数进行考虑。

4)次要功和热散失的处理方法。热散失、火药气体运动功等形式的次要功用次要功计算系数来修正。

5)由于点火药量较少，假设喷孔打开后，流出气体均为主火药燃烧产生的气体。

6)气体在燃气室和发射腔内的流动为轴向和径向的二维无粘流动;燃气室和发射腔内气体参量均为轴向z、径向r 的函数。

1.3 数学模型

基于以上假设，建立数学模型如下:

1.3.1 火药燃烧模型

火药燃速定律

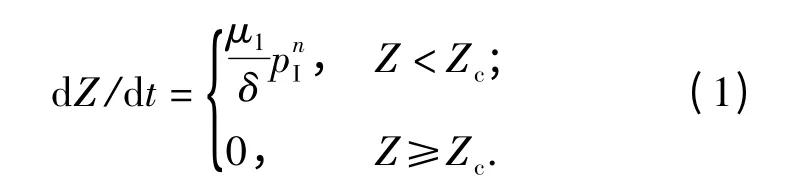
火药形状函数

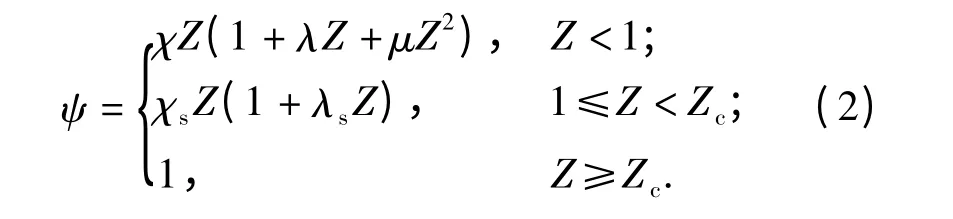
(1)式和(2)式中:Z 是火药已燃相对厚度;Zc为火药燃完时的燃去相对厚度;pI是药室内平均压力;μ1是火药燃速系数;n 是火药燃速指数;δ 是火药弧厚的一半;ψ 是火药已燃质量百分数;χ、χs、λ、λs、μ 为火药形状特征量。

1.3.2 药室内气体状态方程

根据诺贝尔-阿贝尔方程，建立药室内火药气体状态方程

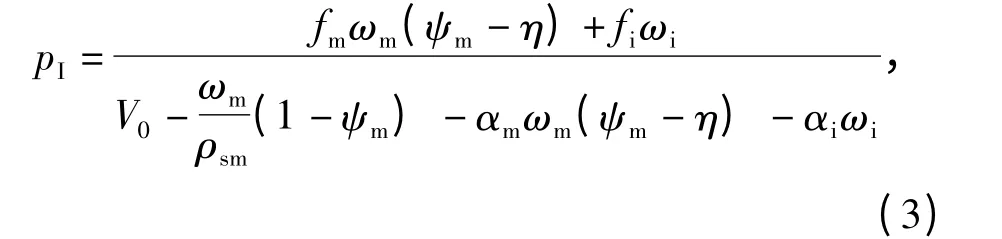
式中:V0为药室容积;ρsm为主火药固相时密度;f、ω、α 分别为火药力、火药质量和余容，下标m 和i 分别表示主火药和点火药;η 为药室流入燃气室内的火药气体流量百分比。

1.3.3 药室内气体通过小孔流入燃气室内的流量方程

单位时间的质量流量

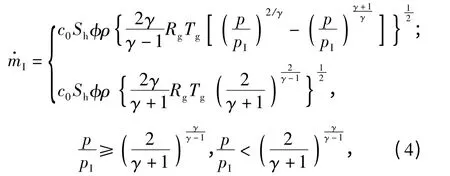
式中:Sh为小孔的总面积;c0为流量系数;γ 为绝热指数;p 为孔流出端压力;Rg为火药气体常数，Tg、ρ分别为火药气体温度和密度;φ 为气相空隙率。

一段时间内单位时间的质量流量百分数为

1.3.4 柱坐标下二维气相基本方程

燃气室和发射腔内用二维气相模型求解。将矢量形式的守恒方程在柱坐标系下展开，得到该坐标系下的二维气相内弹道守恒方程。

1)质量守恒方程

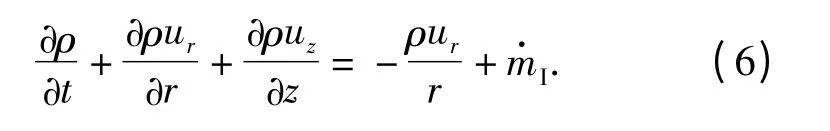
2)动量守恒方程

轴向

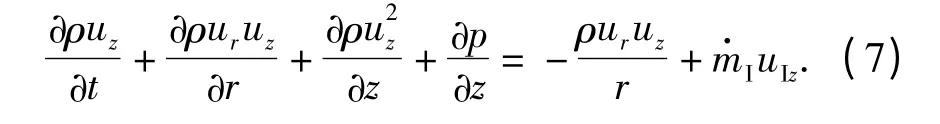
径向

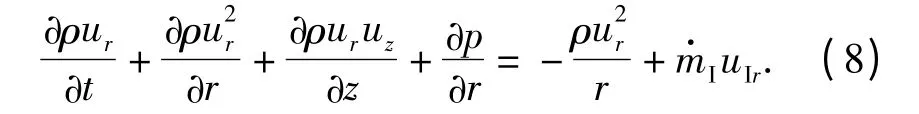
3)能量守恒方程

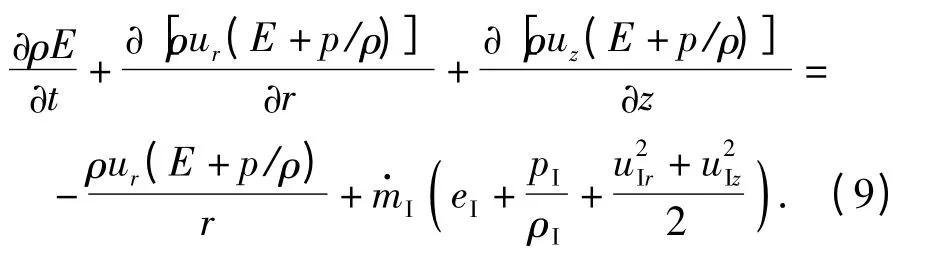
(6)式～(9)式中:ur、uz分别为火药气体径向和轴向速度;E 为气体能量;uIr、uIz、ρI、eI分别为从药室流入的火药气体的径向速度、轴向速度、密度和比内能。

辅助方程

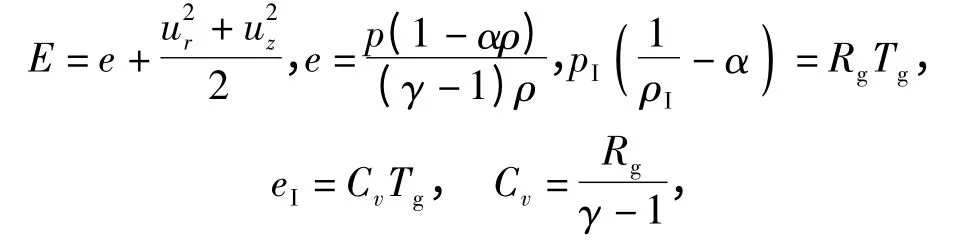
式中:e 为火药气体比内能。

1.3.5 弹丸运动方程

弹丸速度方程

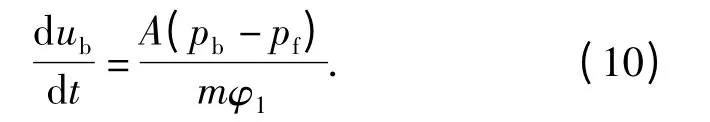
弹丸位移方程

(9)式～(10)式中:pb、pf为弹底压力和弹前阻力;m 为弹丸质量;φ1为次要功系数;ub为弹丸速度;zb为弹丸行程;A 为弹底截面积。

1.4 定解条件

开始时，空间参量都按照实际情况和环境条件给定。壁面边界条件采用第一网格系中的反射法。弹底边界采用运动控制体方法处理。中心轴处满足轴对称关系式［6-7］。

2 数值模拟与结果分析

采用4 阶Runger-Kutta 法［8］计算火药在药室内燃烧的微分方程组及弹丸运动方程。将药室内火药燃烧产生的火药气体量和弹丸运动造成的能量动量消耗，以源项形式加入燃气室和发射腔内建立的守恒方程组，采用Maccormack 差分格式［7］对燃烧室和发射腔内的守恒偏微分方程组进行计算，两种方法交替运行对建立的二维内弹道数值模型求解。点火药采用3#小粒黑，主火药为10 g 3#小粒黑和25 g 2/1 樟火药混合，编制程序得到计算结果。

计算条件与试验条件一致。药室破孔压力约为7 MPa，弹丸启动压力约为13 MPa. 图2给出了燃气室壁上压力传感器测得的压力曲线和计算所得曲线的对比情况，曲线基本吻合，最大压力在18.5 MPa左右。图3为计算所得弹丸速度-时间曲线，弹丸出炮口速度约为83.6 m/s，但实测弹丸出炮口速度分别为73.9 m/s 和76.7 m/s，略小于计算速度，原因在于试验中为避免烟雾干扰，速度的判读在出炮口一定距离处进行。总体上看，计算结果和试验结果较为吻合，所建立的模型和程序合理，可进一步用于流场特性分析。

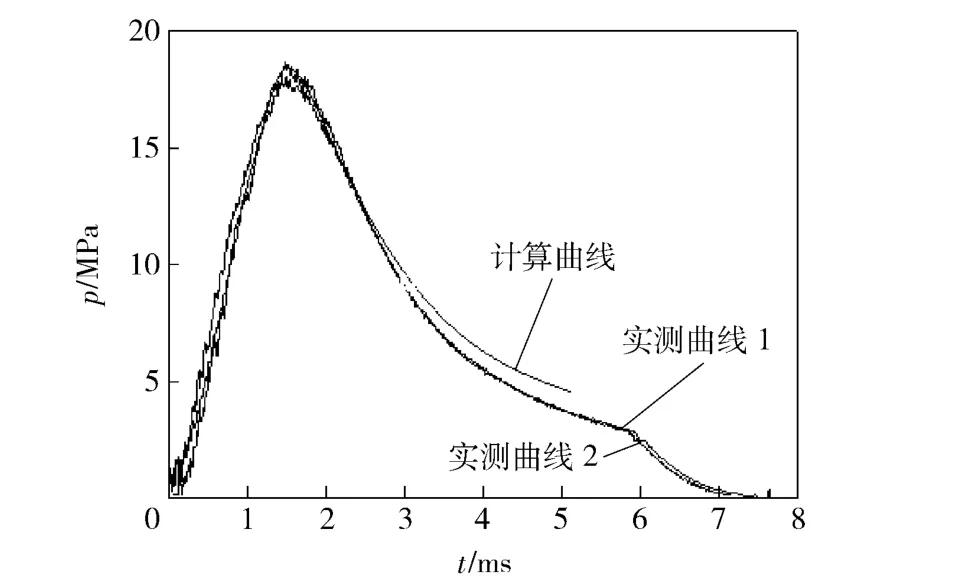
图2 计算结果和实测结果对比图Fig.2 Comparison of calculated and experimental results

图4～图7为弹丸启动前燃气室内气体速度场矢量图。从图中可以看出，弹丸启动前气体流动的规律为:喷孔打开之初，以喷孔流出气体作用范围为界限，气体向径向和轴向剧烈流动，由于燃气室轴向距离短，径向距离长，且气体沿轴向喷出，轴向冲击波首先达到燃气室顶部并开始径向流动，并于下面扩散来的气体汇合向壁面扩散，同时轴向往燃气室顶部流动的趋势减弱。燃气室底部的气体最先达到壁面形成反射波，与向壁面流动的带有轴向反射波的气体混合，形成漩涡流，漩涡流在源源流入气体的作用下继续向边缘运动，强度随着反射波的不断混合得到削弱，流动速度逐渐减弱，在0.286 ms 就已经基本达到稳定混合的状态，此后开始逐渐积聚高压。

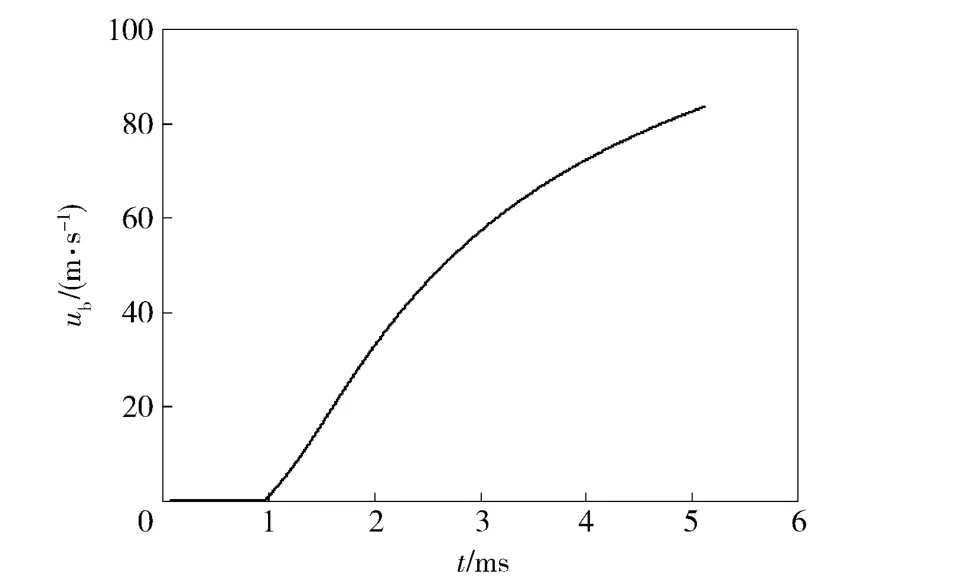
图3 弹丸速度-时间曲线Fig.3 Velocity-time curve of projectile

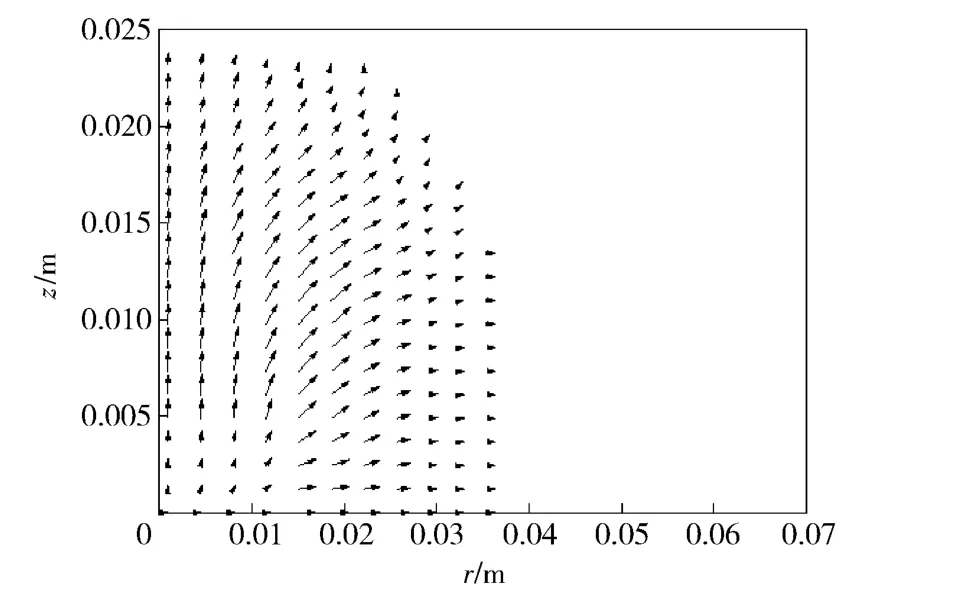
图4 0.087 ms 时气体速度场矢量图Fig.4 Distribution of gas velocity vector at 0.087 ms

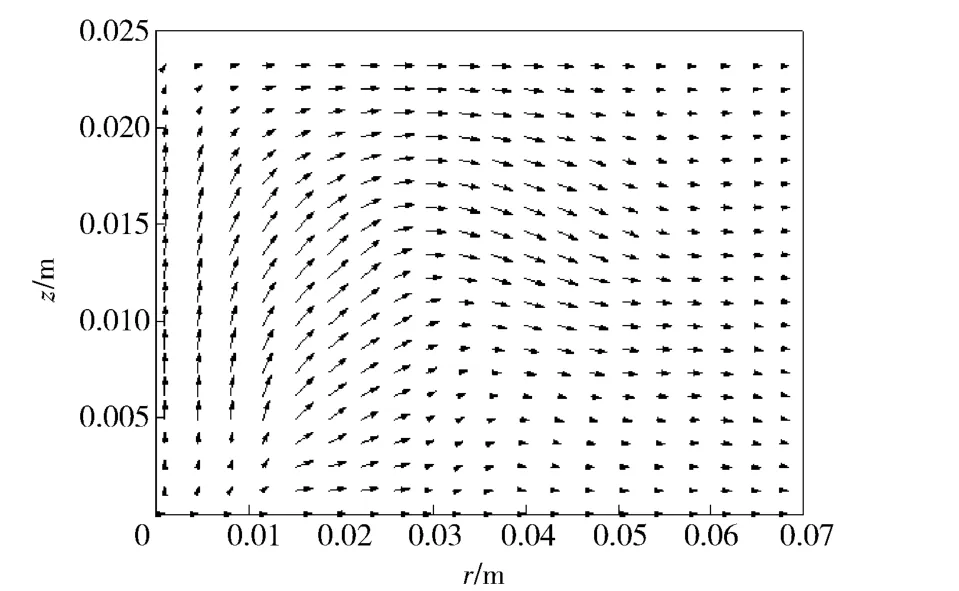
图5 0.144 ms 时气体速度场矢量图Fig.5 Distribution of gas velocity vector at 0.144 ms

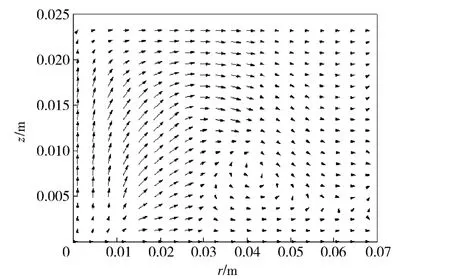
图6 0.213 ms 时气体速度场矢量图Fig.6 Distribution of gas velocity vector at 0.213 ms

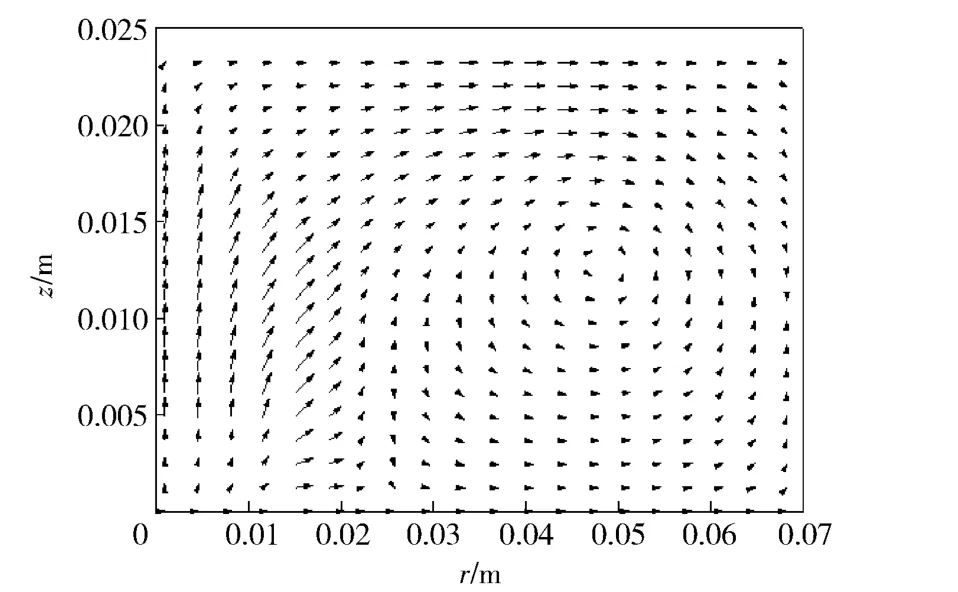
图7 0.286 ms 时气体速度场矢量图Fig.7 Distribution of gas velocity vector at 0.286 ms

气体压力达到一定数值，在0.954 ms 左右弹丸启动。图8和图9为弹丸启动之后的压力变化曲线。弹丸启动时，混合基本稳定的高压气体所占空间开始增大，燃气室内气体往弹底聚集，弹底附近压力增加，扰动形成轴向压力梯度。从图8中可以看出，径向表现为中心轴附近的压力升高。图10 为发射腔底部气体轴向速度分布图，也可以看出，中心轴处气体轴向速度最大，因此形成径向表现为从中间到四周的压力梯度。这一现象与药室在装置中心轴处息息相关。径向压力波动传播到身管侧壁反射，轴向传播到燃气室底部反射，到2.2 ms 时，径向压力梯度几乎消失。图11 为发射腔底部气体径向速度分布图，从中可以看出，径向在此时形成中心处气体向壁面扩散，壁面气体向中心回流的相对稳定流动，而轴向由于弹丸的运动还有部分压力波存在。由图9可得，到这一时刻弹丸行走距离不到0.05 m.图12 为弹丸速度-行程曲线图，从中可以看出，弹丸的加速也主要集中在这段时间内。这说明这段时间内弹后气体压强维持在一个较高的水平，对弹丸速度起主要作用，随着弹后空间的增大，弹体加速逐渐缓慢，从图3可以看出，前一部分速度-时间近似呈线性关系，可见弹后贮存的高压气体保证了弹丸一定的弹射力，将直接影响弹射性能。

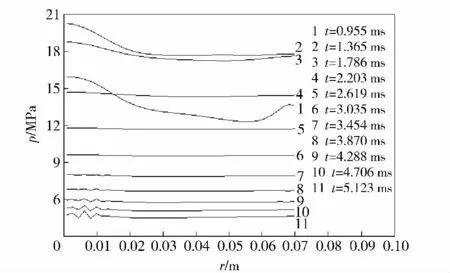
图8 发射腔底部压力分布图Fig.8 Distribution of pressure at the bottom of launching chamber

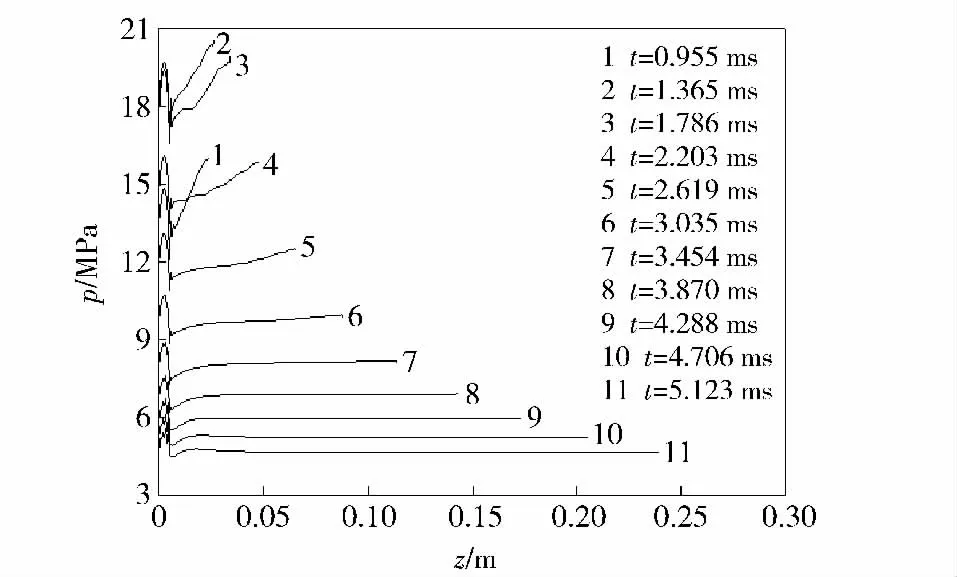
图9 r=8.86 ×10 -4 m 处压力分布图Fig.9 Distribution of pressure for r=8.86 ×10 -4 m

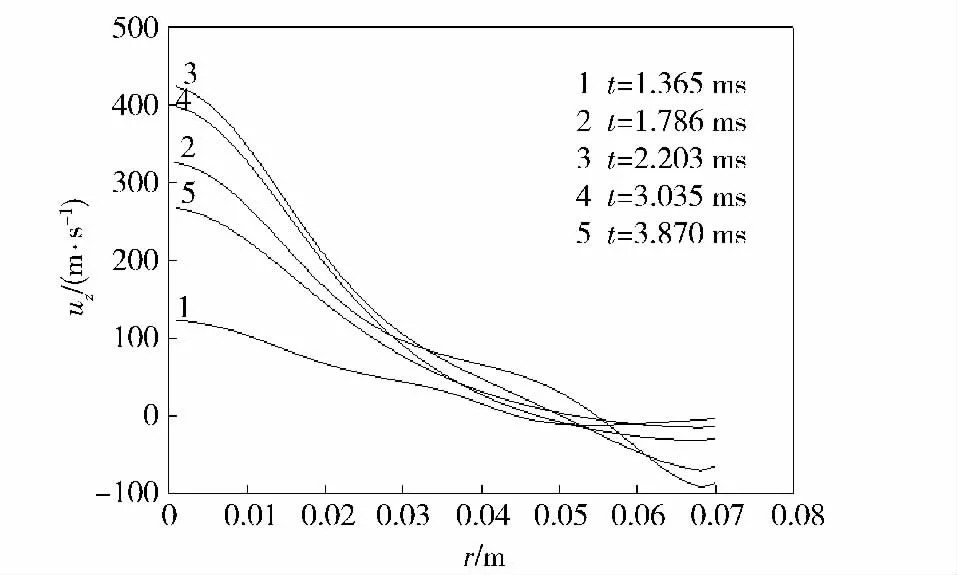
图10 发射腔底部气体轴向速度分布图Fig.10 Distribution of gas axial velocity at the bottom of launching chamber

图13 和图14 为弹丸启动之后气体速度矢量图。从中可见，弹丸运动之后，气体整体流动趋势仍为中心轴和底部气体向四周和上方流动，在斜上方与发射流形成漩涡流的相对稳定流动，由于弹丸的抽吸作用，这个漩涡中心随着弹丸的运动也不断向上方运动。

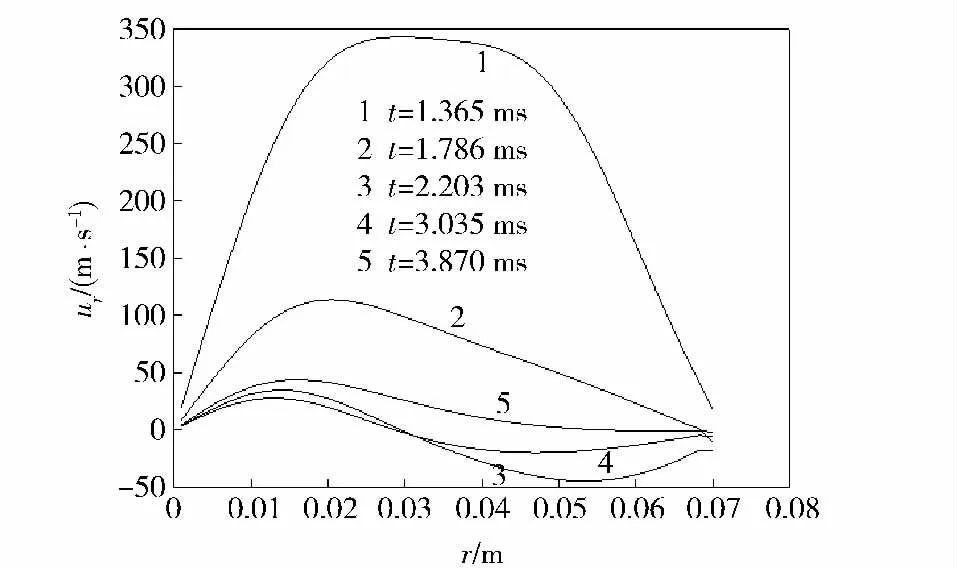
图11 发射腔底部气体径向速度分布图Fig.11 Distribution of gas radial velocity at the bottom of launching chamber

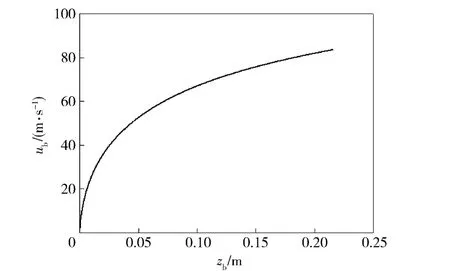
图12 弹丸速度-行程曲线Fig.12 Velocity-distance curve of projectile

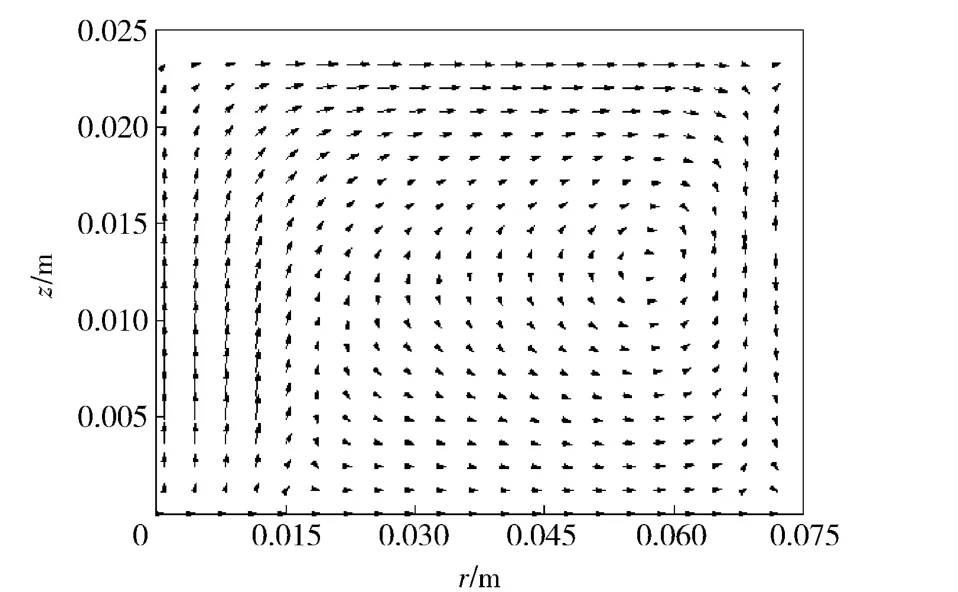
图13 0.955 ms 时气体速度场矢量图Fig.13 Distribution of gas velocity vector at 0.955 ms

3 结论

在研究某高压弹射装置结构和工作原理的基础上，建立了该装置的内弹道二维数值模型，并利用Runger-Kutta 算法和MacCormark 差分格式对其进行了数值仿真，数值计算结果与试验结果较为一致。计算可以得到燃气室和发射腔内各位置气体压力、速度等状态参量的分布，通过对发射腔内的特征参量的分析，掌握其流场特性，得到弹射关键阶段在弹丸启动的较短时间内，高压气体大小和分布是弹丸弹射效果的直接影响因素的结论。下一步将在此基础上对膛口流场的后效作用深入研究，从而为高压弹射装置性能优化设计提供全面参考。

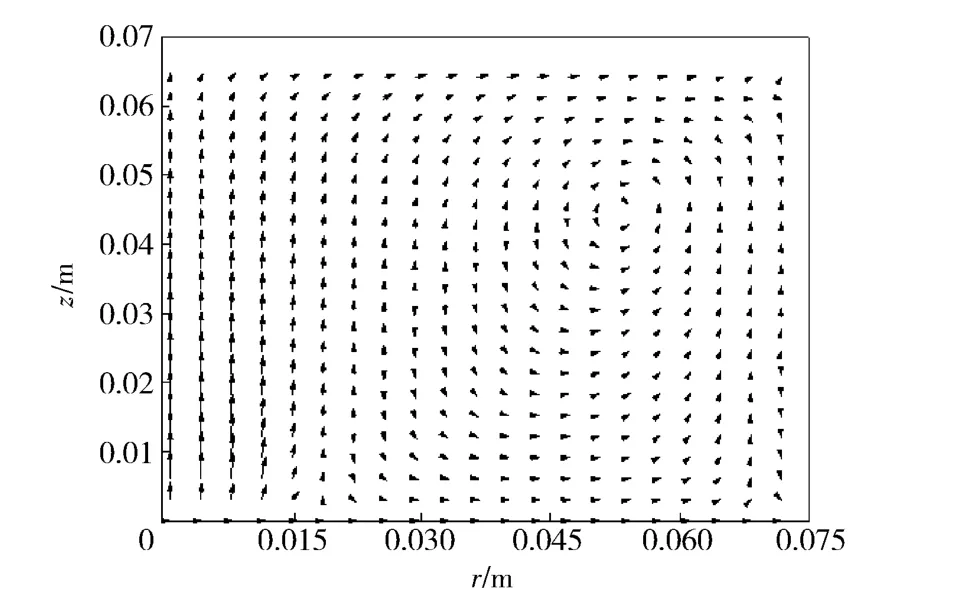
图14 2.619 ms 时气体速度场矢量图Fig.14 Distribution of gas velocity vector at 2.619 ms

References)

［1］杨风波，马大为，杨帆，等.高压弹射装置内弹道建模与计算［J］.兵工学报，2013，34(5):527 -533.YANG Feng-bo，MA Da-wei，YANG Fan，et al. Interior ballistics modeling and calculation of high-pressure ejection device［J］.Acta Armamentarii. 2013，34(5):527 -533.(in Chinese)

［2］郝鑫，王建中，施家栋，等.活塞式高低压发射系统的膛内流场仿真分析与实验［J］.北京理工大学学报，2013，33(10):1005-1009.HAO Xin，WANG Jian-zhong，SHI Jia-dong，et al. Simulation and experiment of interior flow field in piston high-low pressure launcher［J］. Transactions of Beijing Institute of Technology，2013，33(10):1005 -1009.(in Chinese)

［3］韩博，张晓志，邢浴仁，等.大口径火炮发射装药点传火模拟试验装置的研究［J］.兵工学报，2008，29(3):262 -265.HAN Bo，ZHANG Xiao-zhi，XING Yu-ren，et al. Research on simulation testing device of the ignition system for large caliber propellant charging［J］. Acta Armamentarii. 2008，29 (3):262 -265.(in Chinese)

［4］杨正才，廖昕，江坤，等.大口径超短身管高低压发射装置内弹道过程的数值模拟与试验研究［J］. 火炸药学报，2011，34(5):78 -81.YANG Zheng-cai，LIAO Xin，JIANG Kun，et al. Numerical simulation and experimental study on interior ballistics of a large caliber and short barrel launching apparatus with high-low pressure chamber［J］. Chinese Journal of Explosives ＆ Propellants，2011，34(5):78 -81.(in Chinese)

［5］金志明，翁春生.高等内弹道学［M］. 北京:高等教育出版社，2003.JIN Zhi-ming，WENG Chun-sheng. Higherinterior ballistics［M］.Beijing:Higher Education Press，2003.(in Chinese)

［6］宋明，杨新民. 内弹道两相流动计算中两类边界条件的处理［J］.兵工学报，1993，14(3):6 -11.SONG Ming，YANG Xin-min. Two kinds of boundary conditions in two-phase flow interior ballistics numerical simulation［J］.Acta Armamentarii，1993，14 (3):6 -11.(in Chinese)

［7］翁春生，王浩. 计算内弹道学［M］. 北京:国防工业出版社，2006 WONG Chun-sheng，WANG Hao. Computational interior ballistics［M］. Beijing:National Defense Press，2006.(in Chinese)

［8］金志明. 枪炮内弹道学［M］. 北京:北京理工大学出版社，2004.JIN Zhi-ming. Interior ballistics of guns［M］. Beijing:Beijing Institute of Technology Press，2004.(in Chinese)