一种坦克火力单发命中概率的数学计算方法
2015-02-22赵志刚张海军于红娟汤霞清
赵志刚,张海军,于红娟,汤霞清
(1.装甲兵工程学院,北京100072;2.总装装甲军代局,北京100072;3.北方自动控制技术研究所,太原030006)
一种坦克火力单发命中概率的数学计算方法
赵志刚1,2,张海军3,于红娟3,汤霞清1
(1.装甲兵工程学院,北京100072;2.总装装甲军代局,北京100072;3.北方自动控制技术研究所,太原030006)
坦克作为地面陆军装备的主要突击打击力量,精确命中是其发展的首要任务。对于精确命中而言,坦克火力系统衡量的是单发命中概率。从系统工作原理出发,分析影响坦克火力命中概率的误差因素,进而给出一种坦克火力系统命中概率的数学计算方法。
坦克火力系统,误差分析,命中概率
0 引言
坦克作为地面武器中突击作战的精确打击装备,“先敌开火,首发命中”是衡量其作战效能的最重要指标。历次战争实践证明,武器系统打击的命中程度与武器系统作战效能的发挥几乎成正比关系,并且比例系数大于10。由此可见,命中概率在坦克火力系统作战效能发挥过程中起着至关重要的作用。本文依据相关文献,对坦克火力系统误差进行分析,建立命中概率的计算公式,试图在坦克研制工程实践过程中提供参考。
1 射击误差概念
坦克火力系统属于单发射击武器系统,其命中概率是指单发命中概率,即单次射击命中目标可能性的大小。单发命中概率的大小是由射击误差的分布特性和目标的外形特征共同决定的。
坦克火力系统的射击过程可分解为两个过程,即弹丸出膛前和弹丸出膛后。弹丸出膛前的射击误差是由坦克火力系统控制性能决定的,称为射击准备误差;弹丸出膛后的射击误差是由弹丸本身的结构制造特性决定的,是其在外弹道环境作用下的散布情况,称为射弹散布误差。这两个误差共同构成了坦克火力系统的射击误差。
坦克火力系统的射击误差关系如下页图1所示。
坐标中心原点O(0,0)是坦克炮手对目标的理论瞄准点,坐标(x,y)表示其中一发弹射击的实际坐标位置,坐标(x,y)表示本批弹药的散布中心。在和在分别表示其中任何一发弹着点(x,y)和本批弹药的散布中心(x,y)相对与理论瞄准点的射击误差。
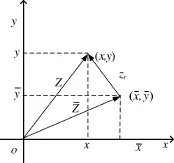
图1 坦克火力系统射击误差关系
在即为射击误差,在水平高低向上相互独立,可表示为:

x表示水平向上射击误差,y表示高低向上射击误差。
对在求其均值

在为射弹散布中心相对与理论瞄准点的误差,称之为火力系统射击准备误差分别表示射击准备误差在水平和高低方向上的分量。
利用三角形原理,得

在r为其中某发弹的射弹散布误差,xr和yr分别表示射弹散布误差在水平和高低方向上的分量。
2 坦克火力系统误差分析
以某稳像式坦克火力系统为例,该系统是由观瞄测系统、计算机及传感器分系统和火炮控制分系统组成的坦克火力系统,组成框图如图2所示。在对敌射击过程中,先由观瞄测分系统测定目标距离和相对运动角速度,将测定数据送给计算机;计算机及传感器分系统根据目标距离及各传感器采集数据计算修正量,给出射击提前量;射击提前量到达火炮控制系统时,使炮身管到一定的发射方向,然后发射炮弹,炮弹飞行到目标位置。
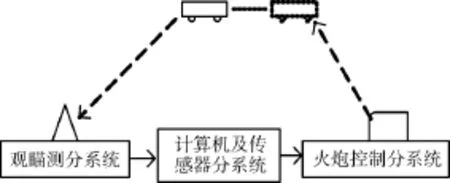
图2 坦克火力系统组成框图
由图2可以看出,坦克火力系统射击准备误差就是由上述3个分系统共同作用产生的,瞄准精确性、解算正确性和控制准确性称为射击命中三要素。根据命中三要素对误差进行分类如下:
(1)瞄准精确性误差:目标中心判定误差,目标跟踪误差和瞄准线双向稳定误差。
(2)解算正确性误差:初速修正误差,偏流误差,气温修正误差、药温修正误差、气压修正误差、横风修正误差、激光距离测量误差,目标角速度测量误差、计算机解算精度误差等。
(3)控制准确性误差:火炮双向稳定精度误差、射击门精度误差和镜炮同步误差。
对上述三类误差分别在水平和高低向上相互独立,从函数角度可分别表示为:
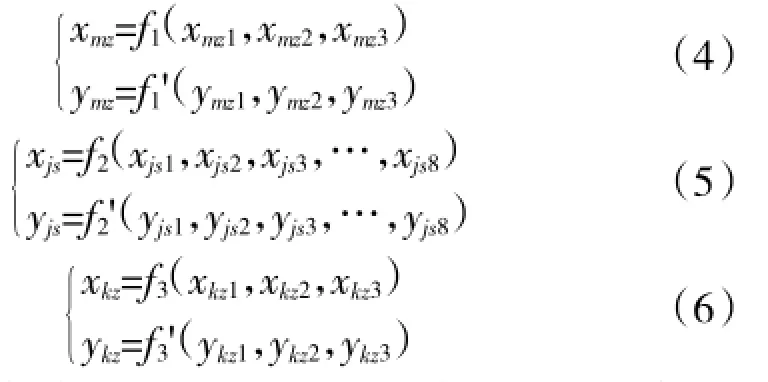
当坦克射击时,系统各误差源产生的误差都是相互独立且非重复的,故在对地面目标射击时,其射弹散布近似可认为是服从正态分布,且在高低和水平方向上相互独立。其射击准备误差为mx、my,射弹散布误差为Ex、Ey(或均方差δx、δy),并且弹着点散布误差分布密度为φ(x,y),在x轴、y轴上的分布密度分别为φ(x)、φ(y),那么
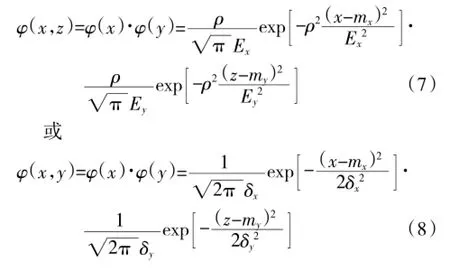
3 单发命中概率的精确计算
现在假设射击目标为矩形目标,目标的方位和高低向大小分别为2lx和2ly,并分别平行于坐标x轴和y轴;目标中心与理论瞄准点O重合;在x轴、y轴上的射弹散布误差分量Δx、Δy相互独立。
对此矩形目标射击的单发命中概率P(x,y)为:
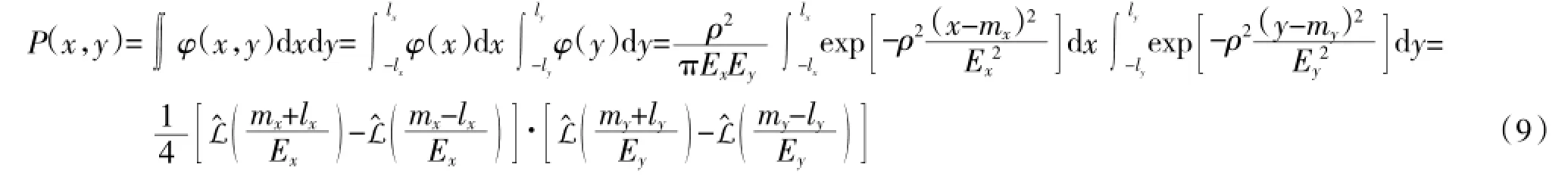
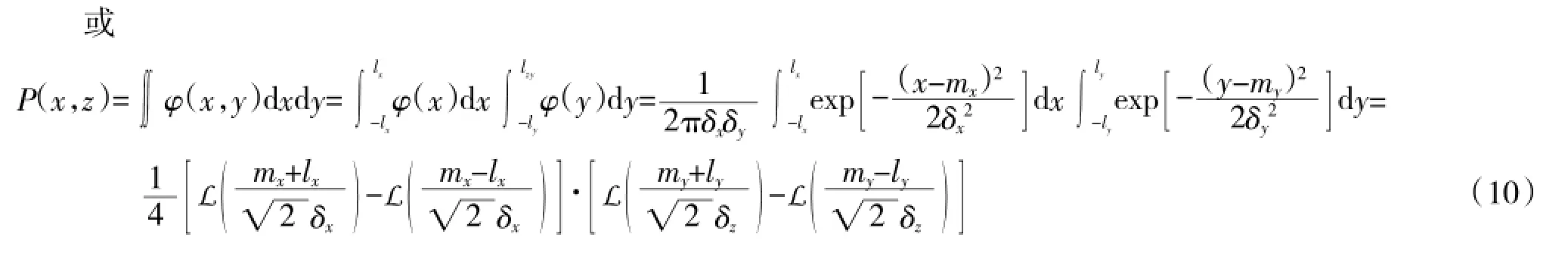
R为矩形目标面积

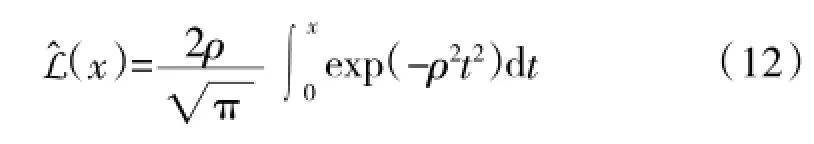
L(x)为拉普拉斯函数

当射弹散布中心与理论瞄准点重合,概率误差等于零,即mx=my=0时,式(12)或式(13)变为:
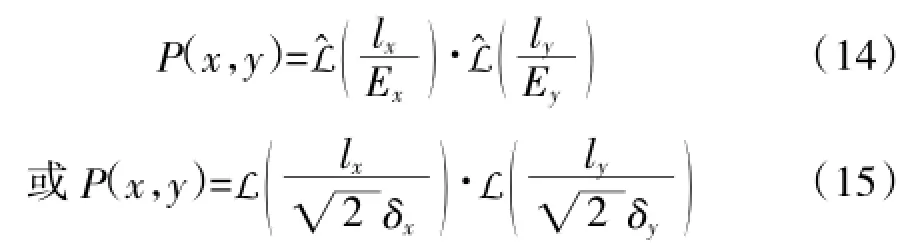
4 结论
本文给出的一种坦克火力系统单发命中概率的计算方法,结构简单,计算方便。理论上能够根据采集的射击误差对坦克火力命中概率进行计算,在仿真分析中具有一定的应用价值。
[1]朱竞夫,赵碧君,王钦钊,等.现代坦克火控系统[M].北京:国防工业出版社,2003.
[2]祁文哲,吴庆立,吴秋轩,等.战车火控外弹道实时解算的研究[J].火力与指挥控制,2001,26(4):15-19.
[3]王兆胜,郭锡福.诸元精度与密集度对命中概率的影响[J].弹道学报,2003,15(1):64-68.
[4]许刚.稳像火控系统误差研究[D].上海:华东工业大学硕士论文,2008.
A Mathematics Calculation for Tank Fire Single Hit Probability
ZHAO Zhi-gang1,2,ZHANG Hai-jun3,YU Hong-juan3,TANG Xia-qing1
(1.Armored Force Engineering Institute,Beijing 100072,China;
2.The Armored Military Representative Bureau of General Armament Department,Beijing 100072,China;
3.North Automatic Control Technology Institute,Taiyuan 030006,China)
As a major assault of ground army equipment against the strike force,its precise hitting is the primary task for the development of tank fire system.For a precise hit,a measure of tank fire system is the single hit probability.From the system working principle,the article analyses some error factors influencing tank fire hit probability,and gives a mathematic calculation method about tank fire single hit probability.
tank fire system,error analysis,hit probability
TJ811
A
1002-0640(2015)01-0115-03
2013-11-05
2014-02-15
赵志刚(1985-),男,山东广饶人,在读硕士研究生。研究方向:坦克火控系统。
