不同结构射弹高速入水稳定性分析

2019-12-03黄鸿鑫张会锁

兵器装备工程学报 2019年11期

黄鸿鑫,张会锁,魏锦，张帆

(1.中北大学机电工程学院，太原 030051；2.中国船舶重工集团公司第七一三研究所，郑州 450000)

射弹高速入水及其稳定性研究仍是国内外一大热点和难题，尚有许多理论、数值模拟以及实验等方面的难题需要解决[1]。射弹高速入水稳定性理论研究主要有以下三个方面：

一是射弹高速入水超空泡发展过程研究。G.V.Logvinovich等[2]描述了空泡截面独立扩张原理对空泡发展过程；Tadd T Truscott等[3]对高速倾斜入水空泡形态和空泡发展过程进行了研究；M.Lee等[4]利用能量守恒原理对射弹高速入水空泡生成、发展过程及闭合特性进行了研究；Michael Dean Neaves等[5]在Euler方程的基础之上，通过引入自然超空化计算模型和Tait状态方程，对射弹高速垂直入水时的空泡形态和发展过程进行了数值模拟；秦杨等[6]对超空泡射弹高速倾斜入水的空化流动进行了数值模拟；王瑞琦等[7]对不同头型弹丸低速垂直入水开展了实验研究。

二是射弹高速入水冲击与水动力研究。王永虎等[8]对不同头型弹体的入水冲击力进行了研究；王冰等[9]提出了耦合非线性自由液面的方法仿真计算入水问题。

三是射弹入水稳定性影响因素研究。王泽宇[10]应用FLUENT软件VOF模型开展了射弹带攻角和旋转过程的数值模拟；张伟等[11]开展了35～160 m/s速度下的入水实验，研究了3种不同头型射弹入水过程的稳定性。

目前，国内外对于入水空泡形态的发展过程和入水冲击及水动力的研究较为深入，而对入水稳定性影响因素的研究相对较少，尤其对于射弹速度大于200m/s入水稳定性影响因素的研究更少，射弹的高速入水给试验研究造成了很大的困难，因此采用理论分析和数值模拟成为解决该类问题最有效的手段。本文将通过有限元分析软件ABAQUS/Explicit，建立射弹高速入水有限元模型，针对射弹的头部形状和射弹的质心位置对射弹高速入水稳定性影响展开分析研究，从空泡形态、速度衰减以及俯仰角变化这个三个方面来考察射弹入水后弹道稳定性。

1 入水模型正确性验证

1.1 有限元模型建立及材料设置

图1 入水物体模型示意图

空气和水材料模型为ABAQUS中的Us-Up状态方程，空气和水材料模型参数如表1所示，线性Us-Up Hugoniot形式的Mie-Gruneisen状态方程[14]来描述水介质的体积响应，其常用形式为：

p-pH=Γρ(Em-EH)

(1)

(2)

表1 空气和水材料参数

常用的对材料雨贡纽曲线拟合关系为：

(3)

式(3)中，c0、s为定义线性冲击波波速Us、粒子速度Up关系的系数。其关系为：

Us=c0+sUp

(4)

进而得到线性Us-Up Hugoniot形式的Mie-Gruneisen状态方程，其表述为：

(5)

由于弹丸在入水过程中不会出现明显变形[13]，因而，在不影响计算结果准确性的前提下，为了提高计算效率，将弹丸设置为ABAQUS中的离散刚体，定义其密度、弹性模量值和泊松比如表2所示。

表2 射弹材料参数

1.2 计算结果对比分析

图2为试验与数值模拟的空泡形态结果，空泡的整个发展历程经历了从运动体撞击水面后空泡流动的形成、空泡充分发展、空泡壁面扩张到最大直径后开始闭合到最后空泡完全闭合的整个过程，且试验结果与数值模拟结果吻合较好，说明本文所采用的有限元模型时准确可靠的。

从图2中t=12 ms可以看出，在模型头部撞击水面以后，在水面以上形成一层水幕，即喷溅[15]。随着时间的推移，喷溅先是向上和向外迅速运动，当向外扩张速度减小到零时开始向中间收缩，最后在入水点上方汇聚到某一点，并形成一个拱形圆顶，如图2中t=55 ms时刻所示。

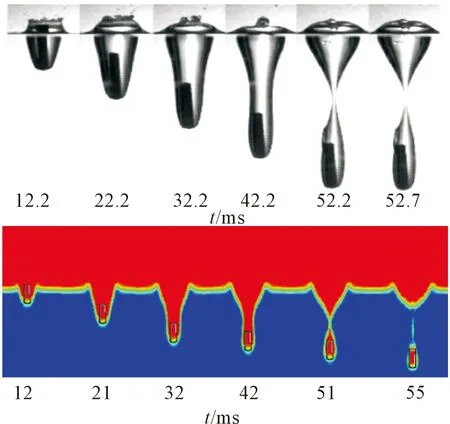
图2 试验结果与数值模拟结果

2 射弹结构对入水稳定性影响分析

2.1 有限元模型建立

为了研究射弹结构对入水稳定性的影响，将设计几种不同结构的射弹模型以400 m/s入水速度和30°入水角度进行数值模拟，空气、水和射弹的空间相对位置如图3所示。射弹结构包括射弹的质心位置和射弹的头部形状，其中质心位置是质心距离弹顶的距离。为了保证射弹在相同质量的条件下质心位置不同，本文将射弹内部进行挖空，通过调整空穴的位置以达到相同质量的射弹、质心位置不同的目的。不同射弹的结构示意图如图4。

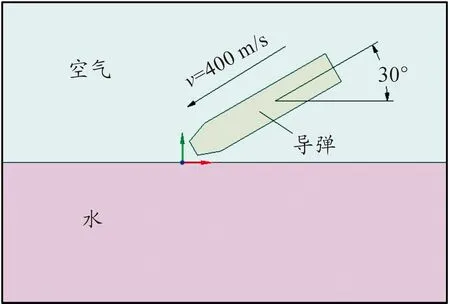
图3 空气、水和射弹的空间相对位置示意图

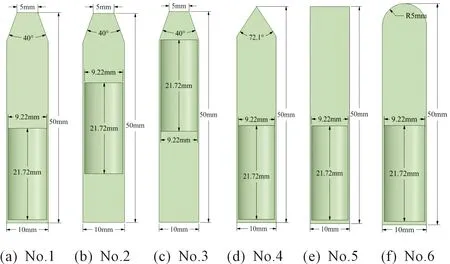
图4 不同结构射弹示意图

共设计了4种不同头部形状的射弹，分别为截锥形、锥形、圆柱形以及半球形，射弹参数如表3所示。在不影响观测空泡发展的前提下，将水域和空气域设计成斜置长方体形状如图5所示，斜置角度为射弹的入水角度，其尺寸与空泡发展过程中的最大尺寸相近，目的是为了省去计算域中不必要空间的网格数量，以提高网格利用率。同时为避免模型边界影响计算结果，在水域和空气边界上施加无反射边界。

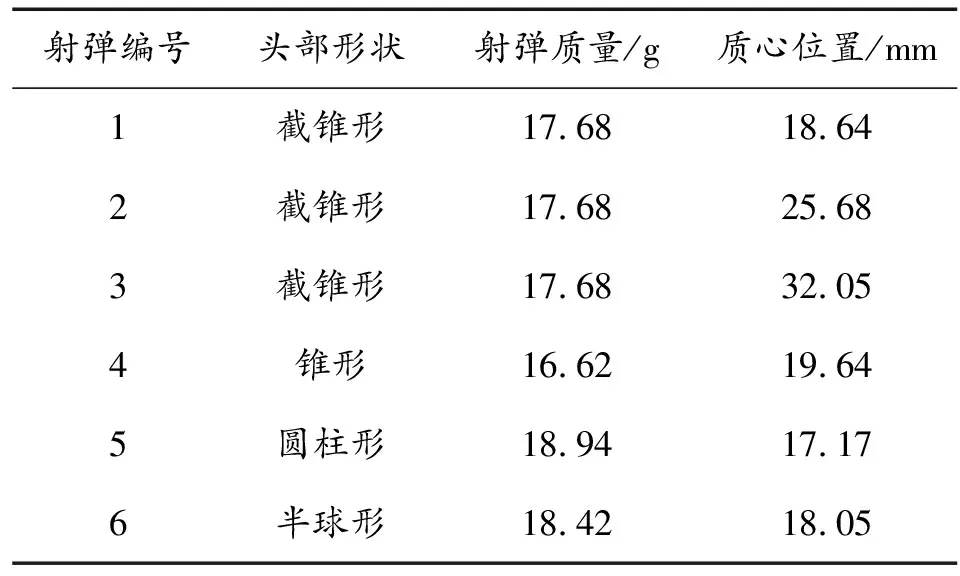
表3 不同结构射弹参数

2.2 数值模拟结果

图5给出了6种不同结构射弹入水过程，射弹入水过程经历入水冲击、空泡形成、开空泡3个阶段[16]。由于射弹是以30°入水，喷溅具有明显的不对称性如图5(a)所示，产生不对称现象的主要原是因为射弹具有较高的水平方向的速度分量，导致射弹与水面接触附近的流体时获得了较大的沿水平方向的动量。各射弹的入水初期姿态具有较好的一致性，但随着入水过程的继续进行，4号和6号射弹姿态发生了较大变化，弹轴几乎与水平轴平行，最终水下弹道彻底失去稳定，导致失去稳定性的主要原因锥形和球形在空泡形成阶段形成的空泡最不理想，使得射弹在入水初期就发生了强烈尾拍[17]，从而使得入水弹道出现了不稳定现象。

除去4号射弹和6号射弹入水不稳定之外，1号、2号、3号射弹和5号射弹稳定性较好，但1号、2号和3号射弹都发生轻微的尾拍，使得空泡壁面产生了上下不对称现象，射弹的质心位置是影响射弹尾拍的重要因素。质心位置靠前的1号射弹，首先与空泡的下壁面发生了尾拍，随着运动的继续又与上壁面发生了尾拍，如图5(a)所示；2号射弹也首先与空泡下壁面发生了尾拍作用，但未与空泡上壁面发生尾拍，如图5(b)所示；3号射弹与空泡上壁面发生尾拍，尾拍后弹轴方向持续向下未且未与下壁面发生尾拍，如图5(c)所示；而5号射弹入水稳定性最佳，整个入水过程未发生尾拍，空泡上下壁面具有良好的对称性，如图5(e)所示。

根据图6(a)可以看出，1号、2号和3号射弹合速度衰减基本一致，速度衰减最快是入水稳定性最差的4号和6号射弹，原因是由于弹道不稳定，使得整个弹体完全处于浸湿状态，阻力大大增加；而5号射弹虽有良好的入水稳定性，但其入水后的速度衰减也很大，说明5号射弹在水中运动时受到的阻力最大。图6(b)～图6(d)为射弹入水后的速度分量，图6(d)体现了射弹在水下运动时的偏航速度，其中偏航速度变化最大的是4号射弹和6号射弹，也说明4号射弹和6号射弹的入水后运动时是存在偏转运动的；偏航速度几乎零的1号射弹和5号射弹。

图5 不同结构射弹入水过程

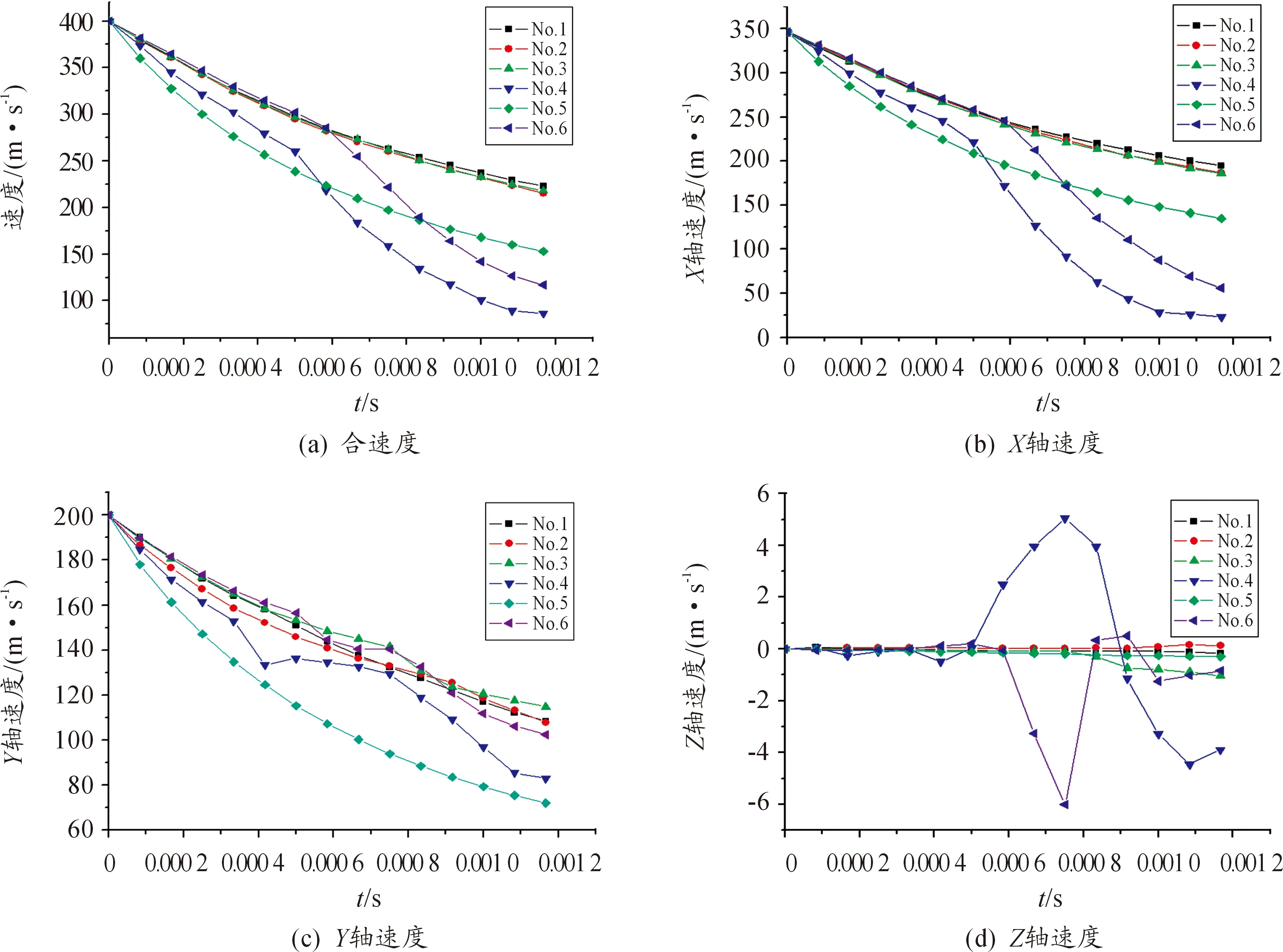
图6 射弹入水速度随时间变化曲线

忽扑是决定射弹水下运动轨迹的重要因素[18]，忽扑实际上就是射弹入水后的俯仰角变化，忽扑影响射弹在入水空泡中的位置，从而很大程度上决定了水下运动轨迹将是下向上弯曲、向下弯曲或是直的，本文俯仰角是正值时表明运动轨迹是向上弯的，负值反之，图7给出了各个射弹的俯仰角随时间变化曲线。由于4号射弹和6号射弹入水的不稳定性，其俯仰角变化最大且为正值如图7(b)所示，说明4号射弹和6号射弹的运动轨迹是严重向上弯曲的。俯仰角变化幅度最小的是1号射弹，从图7(a)中可以看出，1号射弹的两次尾拍造成了俯仰角先正后负。

图7 射弹俯仰角随时间变化曲线

综合对比了6种不同结构射弹的水下运动空泡(如图5)、速度随时间变化(如图6)和俯仰角变化(如图7)，可以得出：对于高速入水射弹，头部形状为锥形和半球形的射弹不利于入水稳定，平头射弹有利于入水稳定，但射弹头部直径过大时，会增大水中的运动阻力，使得速度衰减加快；质心靠前的射弹虽然会增加射弹尾拍次数，但不会出现俯仰角持续处于负值或正值的情况，俯仰角的值会处于0°附近上下波动。