基于排队系统的GERT模型的故障装备数量预测*
2015-02-22邵延君马春茂潘宏侠刘永姜
邵延君,马春茂,潘宏侠,刘永姜
(1.中北大学机械工程与自动化学院,太原030051;2.西北机电工程研究所,陕西咸阳712099)
基于排队系统的GERT模型的故障装备数量预测*
邵延君1,马春茂2,潘宏侠1,刘永姜1
(1.中北大学机械工程与自动化学院,太原030051;2.西北机电工程研究所,陕西咸阳712099)
针对排队维修系统的故障武器装备数量预测的难点,提出了利用GERT随机网络模型对故障武器装备数量进行预测,GERT随机网络模型是一种针对随机变化的系统的一种网络描述,恰好能解决故障武器装备数量的预测问题,准确的故障装备数量预测是武器装备科学管理的一个重要环节。通过实例验证表明,GERT随机网络模型是解决故障武器装备数量预测的一种有效手段和方法。
故障装备,GERT模型,排队系统,维修
0 引言
自Erlang开创排队论至今已经有一百多年的历史,在社会的各个领域得到了广泛的应用,经典的排队论已经是非常成熟的理论,经典的排队论假设顾客的到达过程是泊松过程,到达的时间服从负指数分布,假设服务系统对顾客的服务过程是一个生灭过程,在这些假设的基础上,得到了排队系统中的几个基本数量指标:平均队长、平均排队对长、平均逗留时间、平均等待时间等[1]。在武器装备维修系统中,如果把故障的装备看作是顾客,除了经典排队模型求出的基本数量指标以外,还关心装备维修系统在运行一段时间以后,整个武器装备系统发生故障的数量,以便及时安排备件采购和维修人员调配等工作,以免影响装备的战斗力水平。但经典的排队论理论是无法解决这个问题的,因此,考虑在排队维修系统中引入GERT(Graphical Evaluation Review Technique)随机网络模型来对故障装备数量进行预测。
GERT简称图示评审技术,是一种针对随机变化的环境条件和系统内部随机因素共同作用下对系统的一种网络描述[2-3]。它是将控制论中的信号流图和概率论中的矩母函数等多种理论和方法相融合的一种方法,当前,它已被广泛应用在产品回收、再制造、灾害演化等很多方面[4-6]。本文建立GERT随机网络排队维修系统的仿真模型,来解决故障的武器装备数量预测问题,该模型能将排队维修系统的参数转化为形象直观的网络图,并通过参数的计算来预测故障的装备数量,对武器装备的预防性维修等管理工作具有现实的指导意义。
1 GERT随机网络模型的解析算法原理
1.1 矩母函数
对于任意一个随机变量X,任意一个实数s,令MX(s)是X这个随机变量的矩母函数,并且定义:

1.2 梅森拓扑方程
此方程可以表述如下:
设:Ti,j为由一个节点i到另一个节点j的等价传递系数;xi,xj表示信号流图中节点i到节点j之间的变量值

式中:pk表示由i到j第k条路径上的传递系数;Δk表示消去与第k条路径有关的全部节点和箭头后剩余图的特征式;Δ表示信号流图的特征式;Δ=1-∑T(L1)+∑T(L2)-∑T(L3)+…=1-∑奇阶环的传递系数+∑偶阶环的传递系数。
1.3 GERT网络的传递函数
信号流图原理和矩母函数的特征是形成GERT网络解析算法的基础。令活动(ij)的条件概率密度函数为f(tij),则得到随机变量的条件矩母函数为:

令节点i实现时,活动(ij)被执行的概率为pij;并定义活动(ij)的传递函数为Wij(s),使得:

对具有传递函数Wij(s)的网络,利用信号流图的原理,求解它的等效WE(s)函数,然后根据矩母函数的特征进行换算,就得到了网络图的等价参数PE和TE,在GERT网络中,信号流图原理和矩母函数相互的结合为我们提供了求解随机网络的工具。
1.4 GERT网络求解原理
根据WE(s)=pE×WE(s)
根据矩母函数的特征,当s=0时:

因而,等价概率pE就等于等价传递函数WE(s)在s=0时的值。即:

对于任意的GERT网络,如果能利用梅森公式求解出它的等价传递函数WE(s),则就能相应的求得它的矩母函数ME(s):
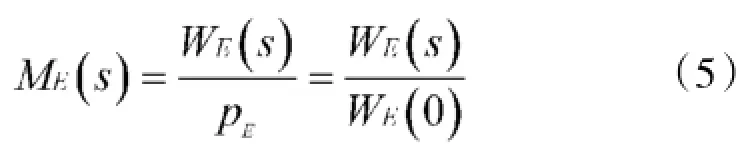
根据矩母函数的n阶导数在s=0处的数值为随机变量的n阶原点矩这一基本性质,有:

因此,对于一个任意的GERT网络,首先收集各项活动的参数,用W函数来描述传递关系,并利用梅森拓扑方程来求解等价概率和等价传递函数WE(s),再根据矩母函数的基本性质,即可反演求得网络的所有参数。这就是GERT解析算法的基本思路,它可以求任意的节点之间的WE(s),也就是能求出任意两个节点之间的PE和TE。
2 GERT网络模型的实例分析
XX防空雷达维修小组负责维修的XX型号雷达共有2台,另有1台备用,以便在出现故障时投入使用。假设每台雷达维修时间和出现故障的间隔时间均服从负指数分布,则该装备维修服务系统符合输入过程为泊松过程,服务时间为负指数分布的随机服务系统,系统容量和顾客总体均为有限,且按先到先服务规则的排队系统,装备维修的过程是可以表示为(M/M/1):(m+n/m/FCFS)排队系统。
假设每台雷达的平均故障间隔时间为1/λ,平均修理一台雷达的时间为1/μ,即λ和μ分别表示平均的故障发生速率和平均修理速率,故障发生速率和平均修理速率之比为λ/μ=1/2,用处于修理和等待修理中的雷达台数来表示该排队系统的状态,用i表示,i=0,1,2,3。
(1)求解状态转移概率
对于状态有限的排队系统,其系统到达速率与服务速率的关系如表1所示:

表1 到达速率与服务速率的关系
故系统由状态i转移到i+1的概率为λi/(λi+μi),而由状态i转移到i-1的概率为μi/(λi+μi),则p01=1;p10=1/2;p12=1/2;p21=2/3;p23=1/3;p32=1。
(2)建立GERT网络模型
由于雷达出现故障的间隔时间和维修时间都服从负指数分布,根据式(2)求各节点间的矩母函数为:

根据式(3)可以得到节点之间的传递函数,从而得到该系统的GERT网络模型如图1所示。

图1 GERT网络模型图
(3)求解在装备维修小组正常工作条件下,来求解从全部雷达均处于正常状态到首次出现雷达全部发生故障,并处于修理或等待修理状态的期望时间(即首次出现i=3的情况的期望时间),这时可将节点3的引出箭头删除,其余各个节点之间的传递函数没有变化,则求得的网络的源节点(0状态)传递到终结点(3状态)的期望时间就是雷达全部发生故障并处于修理或等待修理状态的期望时间。将图1的GERT网络模型图改为图2的网络模型图。

图2 首次出现雷达全部故障GERT网络模型图
首先来求梅森的拓扑方程里面的参数:
①信号流图的特征式Δ为:

②消去第k条路径有关的全部节点、箭头和传递系数后的剩余图的特征式的乘积的和为:

根据式(1)则可以得到0状态到3状态的传递函数为:


根据式(6),对矩母函数求导,令s=0,则可以得到雷达由正常运行到首次全部停止运行的期望时间TE为:

根据这个结果可以预测,整个雷达装备系统由正常运行开始,大约经过7个单位时间,整个雷达装备系统可能会出现全部停止运行的情况。依据上面的步骤和方法,可继续利用GERT随机网络的解析算法,把任何一个状态终结点引出的所有箭头去掉,就可以得到初始状态到任何一个状态的首达期望时间,也就能解决系统运行过程中的故障装备的数量预测问题。可证明GERT随机网络的解析算法是预测故障装备数量的一种有效工具。
4 结论
GERT网络丰富的节点和箭线参数能够对系统进行恰当的描述,能将复杂的系统过程转化为直观形象的网络图。GERT网络模型中的参数能对事件的概率分布进行合理的表达,最重要的是GERT网络能对整个维修系统运用相应的解析算法,进而求出解析表达式,对系统运行一段时间以后的装备故障数量进行预测,根据预测的结果可以为装备的预防性维修等工作提供数据支持,在整个装备系统发生瘫痪前进行科学的预防性维修。
[1]甘应爱,田丰,李维铮,等.运筹学[M].北京:清华大学出版社,2009.
[2]冯允成,吕春莲.随机网络及其应用[M].北京:北京航空航天大学出版社,1987.
[3]Pritsker A A B.Graphical Evaluation and Review Technique[M].Santa Monica:Rand Corp,1966.
[4]Abdi R,Ghasemzadeh H R,Abdollahpour S,et al.Modeling and Analysis of Mechanization Projects of Wheat Production by GERT Networks[J].Agricultural Sciences in China,2010,9(7):1078-1083.
[5]谢家平,赵忠.基于GERT随机网络的废弃回收预测模型研究[J].管理学报,2010,7(2):294-300.
[6]方志耕,杨保华,陆志鹏,等.基于Bayes推理的灾害演化GERT网络模型研究[J].中国管理科学,2009,28(3):39-42.
Prediction for Number of Faulted Equipment Based on Queuing System GERT Model
SHAO Yan-jun1,MA Chun-mao2,PAN Hong-xia1,LIU Yong-jiang1
(1.School of Mechanical Engineering and Automation,North University of China,Taiyuan 030051,China;
2.North West Institute of Mechanics and Electrics Engineering,Xianyang 712099,China)
Aiming at the difficulty to forecast the number of fault armament of queuing maintenance system,this paper proposes the use of GERT random network model to predict the number of fault armament.GERT random network model,a description of randomly changing system,could just solve the problem of predicting the number of faulted armament.Accurate prediction of the number of fault armament is an important part of the scientific management of armament.Experiments show that,GERT random network model is an effective method to forecast the number of fault armament.
fault equipment,GERT model,queuing system,maintenance
TJ307
A
1002-0640(2015)01-0016-03
2013-11-25
:2014-02-19
国家自然科学基金资助项目(51175480);山西省自然科学基金资助项目(2012011046-12)
邵延君(1972-),男,内蒙古赤峰人,博士。研究方向:武器装备的维护与管理、装备故障诊断等。
