电传动装甲车辆电源系统建模与仿真
2015-02-22项宇苏建强刘春光可荣硕赵明
项宇,苏建强,刘春光,可荣硕,赵明
(1装甲兵工程学院,北京100072;2总装备部汽车试验场,南京210028)
电传动装甲车辆电源系统建模与仿真
项宇1,苏建强1,刘春光1,可荣硕1,赵明2
(1装甲兵工程学院,北京100072;2总装备部汽车试验场,南京210028)
电源系统是电传动装甲车辆的核心,对其进行建模与仿真研究具有重要意义。电源系统的非线性特性导致了建模困难、模型精度低以及模型实用性差等难题,针对不同的部件特性采取不同的方法建立其仿真模型,完成了基于模糊控制的系统多目标优化功率分配策略研究。并在此基础上进行了部件和系统两个层次的仿真试验,证明所建模型能够较好地反映电传动车辆电源系统的工作特性。
电传动车辆,电源系统,建模与仿真,功率分配策略
0 引言
电传动具有优越的机动性能和灵活的空间布置适应性,是未来陆战平台发展方向之一[1]。电源系统是电传动车辆的动力源,其供电质量直接影响整车性能[2]。对车辆电源系统进行建模仿真研究,能够检验系统结构及参数设计的合理性,进行功率分配策略研究,提升系统供电品质。
电源系统中的发动机是大惯性非线性环节[3],且系统功率分配依据指标——动力电池SOC易受多种因素影响[4-5],因此,目前对电源系统建模并求解非常困难[6-7],是电传动技术研究的难点之一。本文针对发动机特性提出了实验数据与控制理论相结合的方法,建立发动机动态仿真模型。通过寻找电池端电压、电流与SOC值之间的关系,建立了基于遗传算法优化BP神经网络的动力电池SOC值预测模型。同时完成了发电机和超级电容建模,设计了基于SVPWM的整流控制系统。制定了基于模糊控制的电源系统多目标优化控制策略,并通过部件级和系统级仿真对部件和系统模型进行了验证。
1 系统结构
本文研究对象结构如下页图1所示。各部件主要参数如下页表1所示。
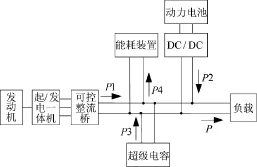
图1 电源系统结构

表1 系统各部件直流侧功率
系统以发动机-发电机组(IGPU)为主能量源,以锂离子动力电池和超级电容作为辅助动力源,动力电池通过单向DC/DC(放电不控,充电可控)与IGPU输出匹配,满足负载功率需求。直流母线并联超级电容和能耗装置,利用超级电容“削峰平谷”,抑制母线电压波动;通过能耗装置消耗过多能量,保证高压安全和系统可靠性。
2 关键部件建模
为满足研究需求,在MATLAB/Simulink环境下建立了电源系统关键部件模型。
2.1 动力电池SOC预测建模
对电池SOC值预测方法研究较多[8-10],而通过寻找电池端电压、电池电流与SOC值之间的关系进行SOC值实时预测是实用且较为精确的方法。但是在试验中获得的电池电流、电压与SOC数据组具有很强的非线性,多项式拟合等方法得到的结果误差较大,而BP神经网络具有无限逼近能力,因此,采用一个具有如图2所示结构的网络拟合实验数据。
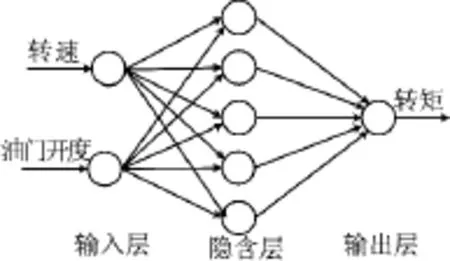
图2 神经网络拓扑结构
在有限训练样本情况下,为保证BP神经网络学习精度,采用遗传算法得到优化的网络最优的权值和阈值,代替网络随机产生的初始权值和阈值。遗传算法按照所选择的适应度函数并通过遗传中的选择、交叉、变异对网络的权值和阈值进行筛选,最终使适应度好的参数被留下来,反之被淘汰。新的权值和阈值不仅继承了上一代的信息,又有了新的变化。通过不断的“择优弃差”,最终满足要求,遗传算法优化BP神经网络程序流程如图3所示。本文以网络预测误差平方作为遗传算法适应度函数S,若SOC为网络预测输出,SOCd为网络期望输出,则
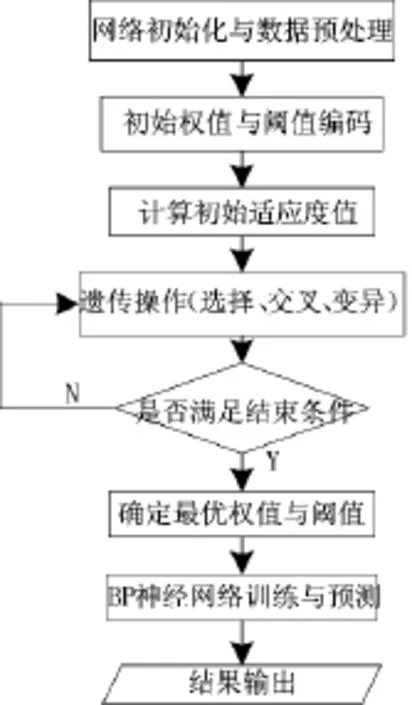
图3 遗传算法优化BP神经网络程序流程

在遗传算法中选取遗传操作次数d=20,种群规模q=10,交叉概率Pc=0.3,变异概率Pm=0.1。使用实验得到的数据对优化后的BP神经网络进行训练,得到最优个体适应度值变化曲线如图4所示,随机选取100组测试数据对训练后的网络预测进行评估。图5为实测数据和预测数据对比,网络预测误差如图6所示。
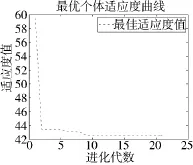
图4 最优个体适应度值变化曲线
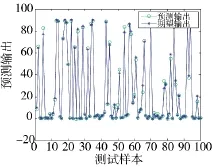
图5 网络预测结果
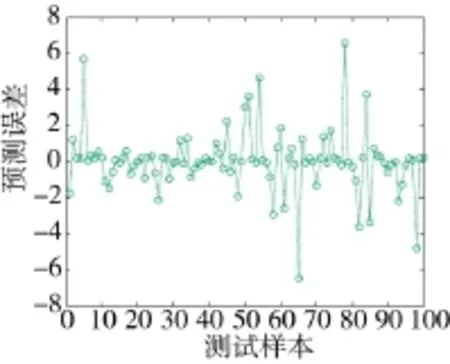
图6 网络预测误差
由图5、图6可知,预测误差大部分小于2豫,在可接受的误差范围内,训练后的网络模型可用于预测锂离子动力电池SOC值。
2.2 发动机模型
发动机内部燃烧过程复杂,影响其动态过程的因素较多,通过对比各类发动机建模方法[11-12],结合课题研究中仅关心发动机的输入输出并有利于控制策略研究这一实际,采用实验数据与控制理论相结合的方法,在发动机稳态模型的基础上,建立发动机的动态特性模型。
采用一个具有如图2所示结构的网络对在实验中获得的发动机转速、转矩和油门开度数据组进行学习。学习结果如图7所示,可作为发动机稳态模型。
发动机稳态模型不能反映发动机各稳态点之间转换过程,而发动机的动态过程对系统控制策略研究影响较大。所以,以发动机稳态模型为基础,建立发动机的动态模型。根据发动机转矩方程(式2),可用于描述发动机的动态过程。
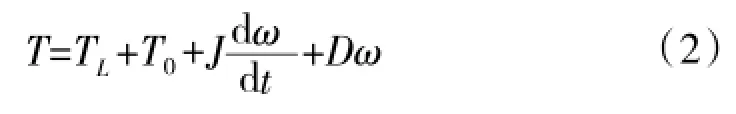
式中,T为发动机输出转矩,TL为负载转矩,T0为空载转矩,J为发动机转动惯量,D为发动机的粘性摩擦系数。
发动机动态仿真模型如图8所示。采用速度闭环控制,通过PID调节器调节油门大小,延迟时间τ指实车油门控制系统的时间延迟。

图8 发动机仿真模型
当恒定负载分别为200 N.m和400 N.m,转速给定阶跃变化时,对发动机模型进行仿真。仿真结果如图9所示。在相同给定条件下,台架实验测得发动机动态响应时间与仿真结果对比,如表2。
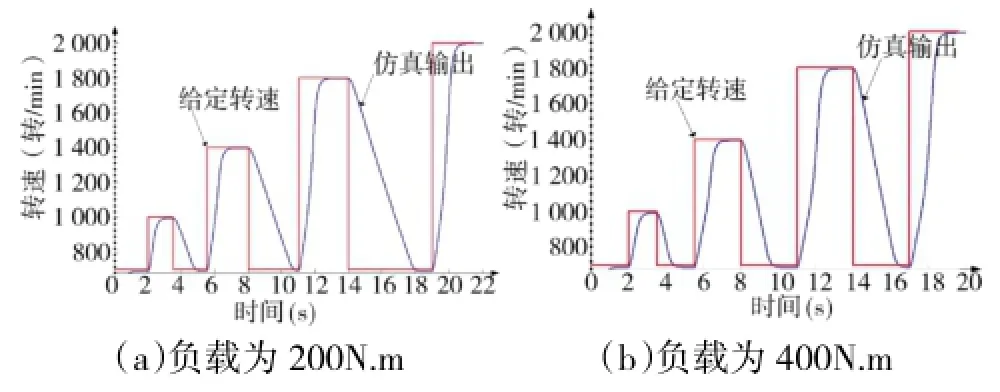
图9 发动机动态响应
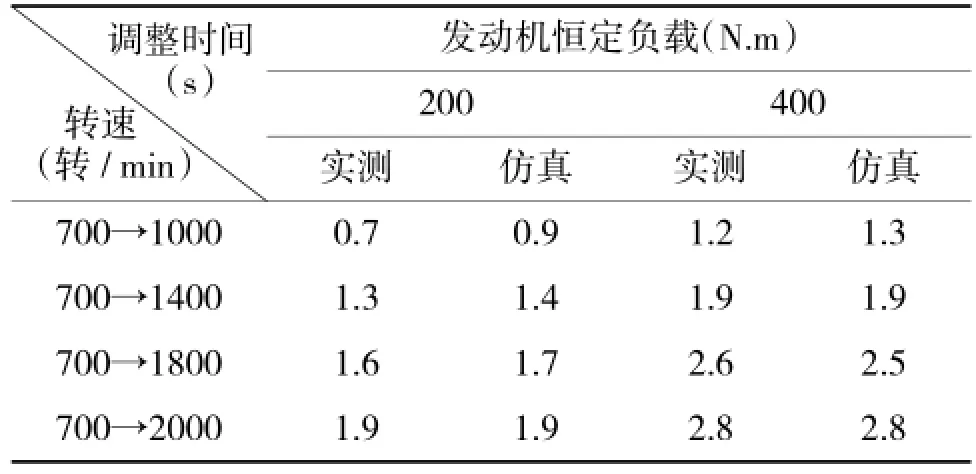
表2 发动机动态响应时间
由图9知,发动机动态模型速度跟踪效果较好。据表2知,发动机动态响应时间和实测值较为接近,误差基本上在0.1 s以内,能够满足研究需求。
2.3 发电机模型及可控整流
在此建立三相永磁同步发电机的数学模型[13]。假设:气隙磁场呈正弦分布;磁饱和效应和涡流损耗忽略不计;不考虑温度变化对电机参数的影响。在旋转坐标系下的永磁同步发电机数学模型为:
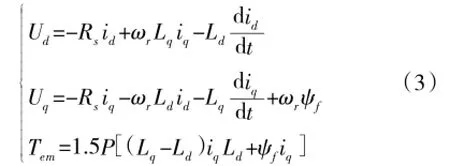
式中,Ud、Uq、id、iq、Ld、Lq分别是定子电压、电流、电感的d、q轴分量;ωr为电机的电角速度;Ψf为转子磁链;Tem为发电机电磁转矩。
发电机输出三相交流电,经可控整流输出直流电,在此采用如下页图10所示的三相VSR PWM整流控制系统。该系统采用双闭环控制结构,外环根据直流侧给定电压vdc_gd和反馈电压vdc比较结果经PI调节器给定q轴给定电流iq_gd;内环跟据d、q轴给定电流id_gd,iq_gd以及反馈电流id、iq,得到交直轴给定电压vd_gd、vq_gd。采用电压空间矢量脉宽调制(SVPWM)法控制PWM波占空比,提升网侧功率因数和系统动态响应速度。
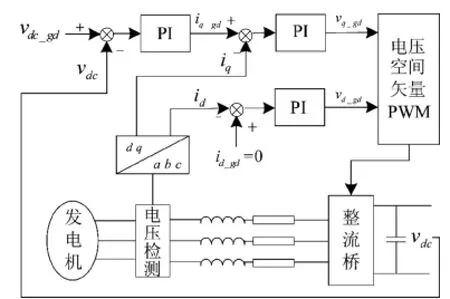
图10 整流器控制方案图
对发电机及整流系统进行仿真,参数设置为:发电机转速1 300转/min,vdc=750 V,直流侧负载10 Ω。仿真结果如图11所示。
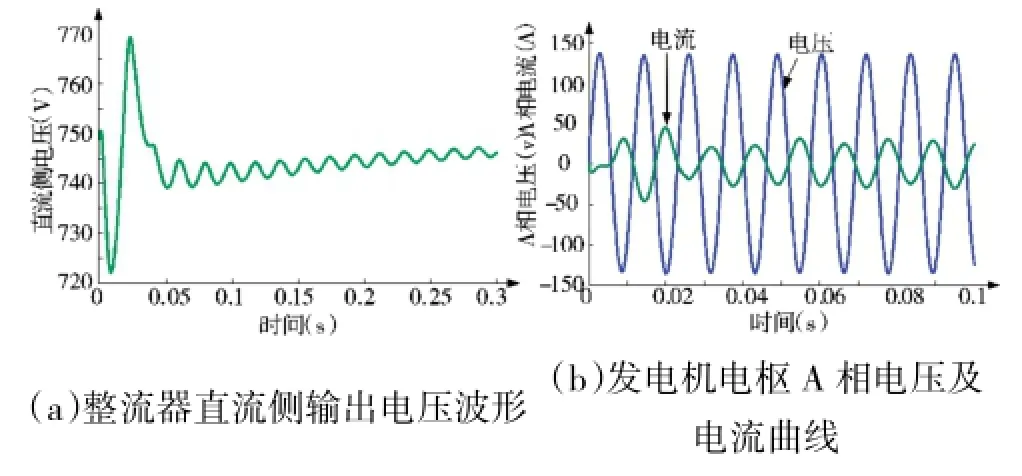
图11 整流控制系统仿真结果
由图11(a)可知,直流侧电压基本稳定在750 V,稳压效果较好;据图11(b)知,发电机电枢A相电压和电流相位相差约180°,网侧功率因数接近-1,提升网侧电压利用率。结果表明该控制方案具有稳压效果好、电压利用率高、动态响应快等优点。
2.4 超级电容模型
由于超级电容工作性能较为稳定,线性程度较高,在电传动技术研究中,一般建立超级电容的等效电路模型[14],如图12所示。
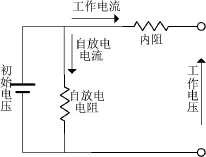
图12 超级电容仿真模型
3 多动力源功率分配策略
仅讨论动力电池、IGPU和超级电容同时工作的混合动力模式,此时系统功率分配采用基于模糊控制的多目标优化控制策略,优化目标有:首先满足负载功率需求;根据负载需求和电池SOC值合理分配各动力源输出;控制IGPU平稳输出,优化发动机工作状态;保持动力电池SOC在65豫~75豫的高效、合理区间,保证车辆随时具备静音行驶能力;储存回馈功率,提高能量利用率。
设计双输入-双输出模糊控制器,输入为负载需求功率P和动力电池荷电状态(SOC)值,输出为发动机-发电机组分配功率P1和动力电池分配功率P2。根据图1中所示的能量流向,依据负载功率P1大小和电池SOC范围,制定如下系统功率分配切换条件:
(1)当0<P<150 kW时
若SOC>75豫时,P1=0,P2=P;
若65豫<SOC<75豫,P1=P,P2=0;
当SOC<65豫时,P1=P-P2,P2=-90 kW;
(2)当150 kW<P<165 kW时
若SOC>75豫时,P1=P-P2,P2=150 kW;
若65豫<SOC<75豫时,P1=P,P2=0;
若SOC<65豫时,P1=P-P2,P2=-90 kW;
(3)当165 kW<P<255 kW时
若SOC>75豫时,P1=P-P2,P2=150kW;
若65豫<SOC<75豫时,P1=P,P2=0;
若SOC<65豫时,P1=255 kW,P2=P-P1;
(4)当P≥255 kW时
若SOC>75豫,P1=P-P2,P2=150 kW;
若20豫≤SOC≤75豫,P1=255 kW,P2=P-P1;
若SOC<20豫,P1=255 kW,P3=0,P3=P-P1;
(5)当P≈0时
若SOC≥65豫,P1=0,P2=0;
若SOC<65豫,P1=-P2=90 kW;
(6)当-90 kW<P<0时
若SOC>90豫,P1=0,P2=0,P3=P;
若65豫≤SOC≤90豫,P1=0,P2=P;
若SOC<65豫,P1=P-P2,P2=-90 kW;
(7)当-230 kW<P<-90 kW
若SOC≥90豫,P1=0,P2=0,P3=P;
若SOC<90豫,P1=0,P2=-90 kW,P3=P-P2。
根据功率分配切换条件,设计的模糊控制器和控制器输入输出关系曲面分别如图13和下页图14所示。
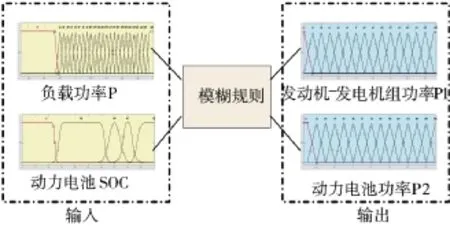
图13 模糊控制器
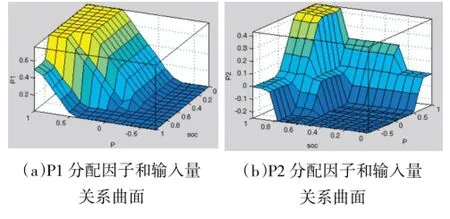
图14 控制器输入输出关系曲面
4 系统模型仿真验证
为验证模型的可行性,根据由各部件模型组成的系统模型和功率分配策略,设置动力电池SOC初始值为50豫,当负载实际需求功率如图15(a)中变化时,系统仿真结果如图15所示(图中所示功率皆为直流侧功率)。
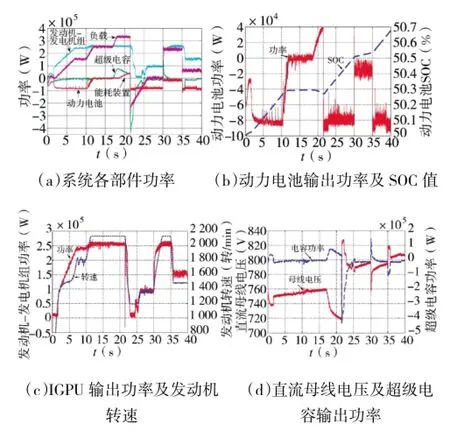
图15 系统仿真结果
如图15(a)所示,各动力源很好地满足了负载功率需求。由于电池SOC小于65豫,因此当系统功率富余时动力电池充电,而当IGPU不能满足负载需求时,动力电池放电。负载突变时,超级电容响应速度较快,很好地起到了“削峰平谷”的作用,直流母线电压在安全范围内变化,如图15(d)。据图15(b)知,动力电池的输出功率和预测得到的SOC值具有很好的一致性,能够体现电池的实际工作状态。在图15(c)中,IGPU输出功率随着发动机转速的变化而变化,符合发动机实际工作特性。系统仿真结果说明了系统功率分配策略的可行性和系统模型的实用性。
5 结论
本文立足于解决电传动装甲车辆电源系统建模难题。通过对系统中的非线性部件进行研究,建立了基于遗传算法优化BP神经网络的动力电池SOC预测模型,采用控制理论与实验数据相结合建立了发动机模型,以及发电机数学模型和超级电容等效电路模型,设计了整流控制方案,并对各部件模型进行独立的仿真验证。最后制定了系统功率分配策略,对电源系统进行了仿真。部件级仿真和系统级仿真结果表明,所建立的电源系统模型能够满足研究需求,制定的系统功率分配策略正确可行。
[1]廖自力,马晓军,臧克茂.全电战斗车辆发展概况及关键技术[J].火力与指挥控制,2008,33(5):1-4.
[2]肖杨婷,赵跃平,曹爽.国内外综合电力系统技术研究动态[J].舰船科学技术,2010,32(8):24-29.
[3]张宏,陈玉春,蔡元虎.液体冲压发动机仿真模型研究[J].计算机仿真,2008,25(7):70-72.
[4]杨阳,汤桃峰,秦大同.电动汽车锂电池PNGV等效电路模型与SOC估算方法[J].系统仿真学报,2012,24(4):938-942.
[5]刘彦中,张奕黄,王大龙,车用动力锂电池的SOC估计[J].电力电子技术,2011,45(12):48-50.
[6]纪锋,付立军,陈海建.基于EMTDC-Simulink的综合电力系统混合仿真[J].船电技术,2008,28(1):1-4.
[7]黄千,黄英,张付军.电传动装甲车辆混合动力总成的联合仿真[J].兵工学报,2007,29(1):10-14.
[8]郭桂芳,曹秉刚.电动车用Ni/MH电池组剩余容量的非线性自回归滑动平均预测[J].控制理论与应用,2011,28(4):591-595.
[9]李司光,张承宁.锂离子电池荷电状态预测方法研究[J].北京理工大学学报,2012,32(2):125-129.
[10]王阔厅,孙俊忠,周智勇.基于RBFNN的船用铅酸蓄电池SOC预测方法研究[J].蓄电池,2012,49(2):76-80.
[11]王存磊,殷承良,王磊.BOOST发动机建模及其在混合动力仿真中的应用[J].上海交通大学学报,2011,45(6):875-880.
[12]杜常清,颜伏伍,严运兵.用于控制的发动机转矩估计方法研究[J].内燃机学报,2008,26(5):446-450.
[13]严干贵,魏治成,穆刚等.直驱永磁同步风电机组的动态建模与运行控制[J].电力系统及其自动化学报,2009,21(6):34-38.
[14]邓隆阳,黄海燕,卢兰光.超级电容性能试验与建模研究[J].车用发动机,2010,183(3):28-32.
Modeling of and Simulation Research on Armored Electric Drive Vehicles Power System
XIANG Yu1,SU Jian-qiang1,LIU Chun-guang1,KE Rong-shuo1,ZHAO Ming2
(1.Academy of Armored Force Engineering,Beijing 100072,China;
2.Automotive Proving Ground,PLA General Arment Department,Nanjing 210028,China)
Modeling of and simulation research are of great significance to power system which is the core parts of Armored Electric Drive Vehicle.The non-liner dynamic characteristic of power system leads to multi-difficulties,such as difficulty in modeling,poor precision and practicability.Different modeling methods are applied in structure modeling of each component in this essay,and system multiobjective optimization power allocation strategy based on fuzzy control is designed.At last,part hierarchy and system hierarchy simulation experiment are carried out,the results demonstrate that the mathematical simulation model reflect the actual performance of the power system.
electric drive vehicle,power system,modeling and simulation,power allocation strategy
TM921
A
1002-0640(2015)01-0178-05
2013-07-05
2013-08-07
项宇(1987-),男,安徽阜阳人,在读博士。研究方向:电传动装甲车车辆能量管理技术。
