双圆阵模式空间二维解相干*

毛维平，李国林，粘朋雷，尹洪伟

（海军航空工程学院，山东烟台264001）

双圆阵模式空间二维解相干*

毛维平，李国林，粘朋雷，尹洪伟

（海军航空工程学院，山东烟台264001）

提出一种相干信号二维波达方向（Direction of Arrival，DOA）估计算法——模式空间波达方向矩阵（Mode-Space DOA Matrix，MS-DOAM）法。算法基于双圆阵，利用模式空间转换将圆阵转换为虚拟双平行线阵，计算虚拟线阵阵元间的互相关信息，构造两个等效协方差矩阵，进而构造波达方向矩阵，对该波达方向矩阵特征分解，利用得到的特征值与特征矢量求得入射信号的仰角和方位角。算法无需二维搜索，实现估计参数自动配对。仿真结果表明，算法在低信噪比和短快拍条件下，估计误差低于虚拟空间平移算法。

阵列天线，均匀圆阵，波达方向，波达方向矩阵，相干

0 引言

均匀圆阵具有能共形于弹体外形、方向图波束形状鲁棒性强、能提供周向方位角信息等优点，使其成为弹载、机载等阵列天线信号处理的研究热点。受多径传播、电磁干扰的影响，会产生大量相干或强相关信号，使子空间类超分辨DOA估计算法性能下降甚至失效。

基于均匀圆阵的相干信号DOA估计算法，主要有阵元域算法［1-4］和变换域算法［5-9］两类。文献［1-2］利用虚拟内插技术产生多个均匀圆阵，依据阵列间旋转不变关系估计DOA，但需要计算内插变换矩阵，优化内插误差，增大了运算复杂度，同时要求较高的信噪比。圆阵虚拟平移算法［3-4］，基于空间平滑原理获得解相干性能，但虚拟平移需严格约束平移距离，空间平滑增大了数据协方差矩阵的计算量。文献［5-6］经过Davies变换［7］，把均匀圆阵转换为虚拟线阵，在模式空间中对虚拟线阵利用空间平滑算法估计相干信号DOA，但空间平滑会损失阵列孔径，而且造成噪声特性变化，不适用于低信噪比场合。文献［8-9］利用模式空间虚拟线阵数据构造Toeplitz矩阵或差分矩阵解相干，避免了空间平滑造成的噪声特性变化和大运算量，而且在数据量少和信噪比低时性能良好，但它们都假定入射信号在阵列平面内，即假定仰角已知，仅估计方位角。

在弹载、机载阵列天线目标定位过程中，接收的有用数据少，信噪比低，而且目标可能在空间中的任何位置，不能将仰角设为定值而仅估计一维方位角，所以上述算法无法获得较好的性能。本文的模式空间波达方向矩阵法继承了矩阵重构算法低信噪比与短快拍数据条件下的优良性能。避免空间虚拟平移算法多次求解数据协方差矩阵和二维谱峰搜索带来的大运算量，与模式空间解相干算法只估计一维参数相比，能完成二维参数联合估计。

1 阵列结构与信号模型

设M个远场窄带点源信号si（t）（i=1，2，…，M）辐射到图1所示阵元数均为N的两个各向同性且均匀分布的半径为R的圆形阵列上，不考虑幅相、互耦等误差影响。（θi，φi）表示第i个信号源的来波方位角和仰角，设噪声为加性高斯白噪声，阵元间噪声彼此独立，且与信号不相关。

以子阵1的圆心为参考点，则子阵1的第k个阵元的输出信号表示为：

式中，k=0，1，…，N-1；n1k（t）为子阵1第k个阵元接收的噪声；则N个阵元输出的矢量形式为：

图1 双均匀圆形阵列结构

同理可得，子阵2的N个阵元输出为：

利用Davies模式空间转换法［7］，分别将式（2）和式（3）两个子圆阵的接收数据转换为虚拟双平行线阵的接收数据可得：

由式（4）和式（5）可知，两个子圆阵相对于在轴形成的旋转因子Φ（φ）与圆阵的可激发相位模式数以及阵元数均无关，所以经模式空间转换后，旋转关系依然存在。

2 算法描述

2.1 构造解相干等效协方差矩阵

定义两个互相关运算：

其中，m=-K，…，0，…，K；（·）*表示共轭算子。依据各阵元噪声之间、噪声与信号之间独立性假设，将式（6）展开可得：

同理，式（7）可写为：

其中，bm+K+1（θ，φ）表示B（θ，φ）的第m+K+1行；2表示第一个虚拟子线阵中心阵元的噪声功率；；（·）H为共轭转置算子；

利用式（8）和式（9）计算的数据构造两个等效协方差矩阵Rxx和Ryx如下：

式（12）与式（8）的不同之处为J-m*（-βi）J0（-βi）和Jm（-βi）J0*（-βi）。由于J-m（-βi）=（-1）mJm（-βi），则对式（4）或式（5）中的模式空间变换矩阵T进行修正

同样，求得修正的互相关信息r'xx（m）和r'yx（m），并以式（10）和式（11）的形式构造矩阵，假设构造的矩阵以R'xx和R'yx表示。此时，r'xx（m）=（r'xx（-m））*、r'yx（m）=（r'yx（-m））*，所以经过修正后重构的矩阵是厄米特矩阵。定义新的阵列流形矩阵B1（θ，φ）：

其中，⊙表示Hadamard积。式（15）表明，对（θi，φi）的二维估计，实际可以分为两个一维估计，前提是能独立地估计出φi，即式中的βi，这就是引入第二个子阵（即双圆阵）的原因，运用波达方向矩阵法［10］可实现φi的独立估计。

现假设φi已成功估计，即J（φ）已知，对式（15）再作变换

J-1（φ）表示矩阵J（φ）各元素取倒数。参见文献［11］，可以证明

式（17）中，I（K+1）×（K+1）是（K+1）×（K+1）阶单位阵。以式（17）为例，说明式（17）和式（18）能对相干信号完全解相干。当i≠j时，φi≠φj，而且φi∈［0，π/2］，由文献［12］第一类bessel函数性质可知，即使Jm（-βi）=Jm（-βj）成立，也有Jn（-βi）≠Jn（-βj），m≠n，所以J（φ）是列满秩的。同样，θi≠θj时，B（θ）列满秩。由式（9）中的S可以得出，当信号源相干时，对角线元素为所有相干信号功率的叠加，当信号源不相关时，对角线元素为对应信号的功率。由于信号不为零，则S为满秩对角阵，只与入射信号个数有关，不受信号相干与否的影响，所以式（17）和式（18）能对相干信号完全解相干。

2.2 运算复杂度分析与算法总结

本文算法利用矩阵重构理论并引入波达方向矩阵法来降低运算量，多次求协方差矩阵和二维谱峰搜索带来的巨大运算量。根据算法流程，本文算法运算量主要由3部分组成：模式空间变换、重构矩阵以及波达方向矩阵法。设快拍数为n，K，（K＜N/2）为可激发的最大相位模式数，则运算复杂度为O（2n×2K×（N2+1）+3K3）。空间虚拟平移算法运算量由计算解相干协方差矩阵、特征分解和谱峰搜索3部分构成，设谱峰搜索精度为σ，运算复杂度为O（n×M×N2+N3+360×91×1/σ×N2）。综上可知本文算法运算量小。将本文算法具体步骤归纳如下：

步骤1：将双圆阵接收的数据矢量X（t）、Y（t）依据式（4）和式（5）转换为模式空间虚拟线阵数据；

步骤2：参照式（6）和式（7）的方法，计算修正的互相关信息r'xx（m）和r'yx（m）；

步骤3：根据式（10）和式（11）构造修正的等效协方差矩阵R'xx、R'yx；

步骤4：依据文献［10］的波达方向矩阵法估计二维来波方向。

3 数值仿真与分析

为验证本文方法的有效性，进行如下3个仿真试验。仿真1验证算法的可行性，仿真2和仿真3试验算法性能对信噪比和快拍数的敏感程度，并与圆阵空间虚拟平移（UCA-VSS）算法［4］作比较。

仿真1验证算法的可行性。假设每个子圆阵阵元个数均为15，激励模式数取6，4个远场等功率相干信号分别从（330°，30°）、（245°，65°）、（140°，40°）、（100°，80°）方向入射到阵列上。固定快拍数为500次，5 dB、10 dB、20 dB信噪比条件下以及固定信噪比为10 dB，快拍数为200次、500次、1 000次时的DOA估计值如表1所示。表1表明，本文算法能估计信号相干时的二维DOA。

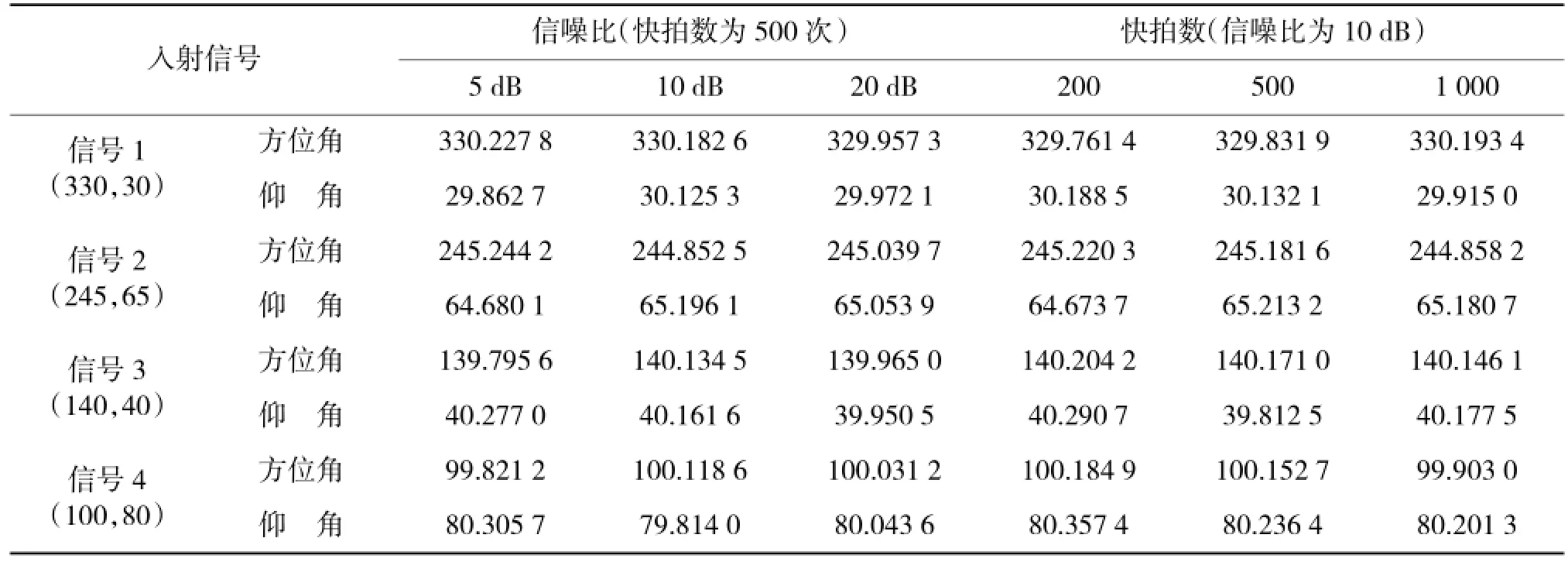
表1 MS-DOAM的二维DOA估计值（单位：度（°））

仿真2验证算法对信噪比的敏感程度。仿真模型和入射信号同仿真1，快拍数固定为500次，从0到20 dB，步进步长为1 dB，在不同信噪比下分别进行200次独立仿真实验，得到本文算法（MS-DOAM）和空间虚拟平移（UCA-VSS）算法方位角与仰角的DOA估计均方误差随信噪比变化情况如图2和图3所示。定义DOA估计均方根误差（root mean square error，RMSE）如下：

其中，θi为入射信号i（i=1，2，3，4）的实际方位角；ij为入射信号i方位角的第j次估计值；n为重复试验的次数，仰角估计的均方根误差定义同理。从图2、图3中可以看出，在低信噪比时，MS-DOAM算法要优于UCA-VSS算法，随着信噪比（SNR）的提高，方位角和仰角估计性能也逐渐提高，当信噪比大于15 dB时，两者性能相当。这是由于MS-DOAM属于矩阵重构类算法，在低信噪比条件下，即具有较好的估计性能，而空间平滑算法适用于高信噪比场合。值得注意的是，UCA-VSS算法通过阵列平移解相干，所以空间虚拟平移过程不造成孔径损失，而MS-DOAM算法，利用波达方向矩阵法来实现方位角和仰角独立估计，增加了一个子圆阵，有阵列孔径损失。

图2 方位角均方根误差随信噪比变化的曲线

图3 仰角均方根误差随信噪比变化的曲线

仿真3验证算法对快拍数的敏感程度。仿真模型和入射信号同仿真1，信噪比固定为10 dB，快拍数从50次到1 000次，以50次为步进步长，在不同快拍数时分别进行200次独立仿真实验，均方根误差定义如仿真2，仿真结果如下页图4、图5所示。随着快拍数的增加，两类算法估计均方根误差逐渐减小，当快拍数大于500次以上时，其估计性能基本趋于稳定。但即使数据快拍大于500次，MS-DOAM算法依旧优于UCA-VSS算法，其原因是MS-DOAM算法构造的协方差矩阵，主对角线上每个元素的噪声分量都是参考阵元的噪声功率，而UCA-VSS算法利用平滑后数据求得协方差矩阵，其主对角线各元素噪声分量是各自阵元的噪声功率，所以MS-DOAM算法能抑制噪声功率的发散性。

图4 方位角均方根误差随快拍数变化的曲线

图5 仰角均方根误差随快拍数变化的曲线

4 结论

本文针对相干信号波达方向估计问题，提出双圆阵模式空间矩阵重构解相干的波达方向矩阵算法。文中将波达方向矩阵法引入均匀圆阵，仅用一次特征分解，实现二维波达方向参数分离估计，估计参数自动配对，避免二维谱峰搜索。算法具有良好的解相干性能，在低信噪比和少量快拍数据条件下，其性能优于虚拟空间平移解相干算法。文中给出的仿真算例验证了算法的有效性。

［1］Friedlander B.Direction Finding Using Spatial Smoothing with Interpolated Arrays［J］.IEEE Trans.on Aerospace and Electronic Systems，1992，28（2）:574-587.

［2］Hyberg P，Jansson M，Ottersten B.Array Interpolation and DOA MSE Reduction［J］.IEEE Trans.on Signal Processing，2005，53（12）:4464-4471.

［3］Xu D H，Chen J W.A Novel DOA Estimation for Uniform Circular Arrays in Correlated Environment Without Interpolation［C］//Intelligent Signal Processing and Communications，2006.ISPACS'06.Tottori，Japan:IEEE，2006:650-652.［4］侯碧波.基于均匀圆阵的2D DOA估计算法研究及实现［D］.成都:电子科技大学，2011.

［5］Wax M，Sheinvald J.Direction Finding of Coherent Signals Via Spatial Smoothing for Uniform Circular Arrays［J］.IEEE Trans on Antennas Propagate，1994，42（5）:613-620.

［6］Akkar S，Harabi F，Gharsallah A.Concentric Circular Array for DOAs Estimation of Coherent Sources with ESPRIT Algorithm［C］//5th International Conference on Design and Technology of Integrated Systems in Nanoscale Era.Hammamet，Tunisia:IEEE，2010:1-6.

［7］Davies D E N.A Transformation Between the Phasing Techniques Required for Linear and Circular Aerial Arrays［J］. IEE Proceeding F，1965，112（11）:2041-2045.

［8］高书彦，陈辉，王永良，等.基于均匀圆阵的模式空间矩阵重构算法［J］.电子与信息学报，2007，29（12）:2832-2835.

［9］谢菊兰，李会勇，何子述.均匀圆阵相干信源DOA估计的差分算法［J］.电子科技大学学报，2012，41（4）:516-521.

［10］殷勤业，邹理和，Newcomb R W.一种高分辨率二维信号参量估计方法——波达方向矩阵法［J］.通信学报，1991，12（4）:1-7.

［11］王凌，李国林，毛维平.一种基于数据矩阵重构的相干信源二维测向新方法［J］.西安电子科技大学学报，2013，40（2）:130-137.

［12］王竹溪，郭敦仁.特殊函数概论［M］.北京:北京大学出版社，2000:381-506.

Two-dimensional De-coherent Mode-space Method Based on UCA

MAO Wei-ping，LI Guo-lin，NIAN Peng-lei，YIN Hong-wei
（Naval Aeronautics and Astronautics University，Yantai 264001，China）

A two-dimensional direction of arrival（DOA）estimation algorithm of coherent signals，called Mode-Space DOA Matrix（MS-DOAM）algorithm，is proposed.The algorithm uses mode-space excitation to transform the UCAs into virtual parallel linear arrays.Then，two equivalent covariance matrices are reconstructed by using cross-correlation information of array elements.A new DOA matrix is reconstructed besed on the two matrices.Eigenvalues and eigenvectors are acquired by performing eigenvalue decomposition of the DOA matrix.According to the eigenvalues and eigenvectors with elevation and azimuth information，the DOA of coherent signals could be estimated.The algorithm requires no parameter alignment and 2-D spectrum peak searching.Computer simulation confirms that the proposed algorithm achieved better performance than UCA-VSS algorithm under scenarios of low SNR and deficient snapshots.

antenna array，uniform circular array，direction of arrival，DOA matrix，coherent

TN911.7

A

1002-0640（2015）01-0019-05

2013-11-15

：2014-02-20

国家自然科学基金资助项目（61102165）

毛维平（1986-），男，四川彭山人，博士研究生。研究方向：阵列信号处理。