香蕉形振动筛激振器强度的有限元分析

安晓卫，解建康，纪玉杰，徐文彬

(1．沈阳理工大学 机械工程学院，辽宁 沈阳 110159；2．鞍山重型矿山机械股份有限公司，辽宁 鞍山 114051)

香蕉形振动筛激振器强度的有限元分析

安晓卫1，解建康1，纪玉杰1，徐文彬2

(1．沈阳理工大学 机械工程学院，辽宁 沈阳 110159；2．鞍山重型矿山机械股份有限公司，辽宁 鞍山 114051)

采用薄板弯曲理论、坐标变换、位移变换、形函数插值等方法，确定激振器的位移边界条件，建立激振器的有限元模型，并对振动筛激振器进行有限元强度分析。经过强度校核，各部件均在安全范围。

插值；有限元；静力学；强度

香蕉形直线振动筛在周期载荷下做受迫振动，易发生疲劳破坏。传统的设计方法不能预知机体在载荷作用下的应力和应变分布，在实际过程中经常发生主梁折断、侧板撕裂、主轴扭曲、机体底座撕裂、螺栓折断等事故。因此对振动筛进行有限元强度分析很有必要。

文献[1-3]建立了振动筛筛箱的有限元模型，得到了香蕉形直线振动筛的动态特性。文献[4]对振动筛筛箱进行了静力学分析。文献[5]以板单元为主建立了振动筛筛箱的有限元模型。文献[6]对激振器进行了模态分析，获得其各阶固有频率与振型，偏心块和激振轴采用附加质量单元，侧板下部采用板单元，侧板上部梁联接部分采用实体单元,横梁采用梁单元。

目前对振动筛强度的研究大都集中在筛箱上，对激振器的研究很少。一是因为筛箱是最易损部件；另外因为振动筛体积庞大，若筛箱和激振器一起进行有限元分析，计算成本很高，以现有的资源很难满足要求，而单独研究激振器，位移边界条件的确定是一个难点。但是当前振动筛正朝着大型化方向发展，结构增大后必然引起激振器的参振质量和激振力增大，机体的动负荷也随之增大，导致激振器的结构强度和刚度不足，严重影响激振器的使用寿命，所以在设计时必须考虑激振器的强度问题。本文根据振动筛整体计算结果，利用插值的方法计算出激振器的位移边界条件，建立激振器有限元模型，并对其进行有限元强度分析。

1 香蕉形振动筛整体有限元计算

振动筛筛箱的外形尺寸：长9.117m，宽4.9 m，高3.49 m。主要由主梁、侧板、上下横梁、后挡板、U型加强板、前后弹簧座耳和支撑角钢等部件组成。采用板单元模拟侧板、上下横梁、主梁等结构件。由于激振器的刚度和强度比筛箱大得多，所以激振器用集中质量单元模拟；激振器与主梁之间由16个高强度螺栓连接，采用刚性耦合来模拟激振器与主梁之间的连接，激振器所产生的激振力通过刚性耦合连接传递到筛箱上；筛箱与地面之间的连接弹簧用弹簧单元。有限元模型如图1所示。计算结果如图2所示，图2为主梁位移云图，即与激振器相接触的主梁位移。

图1 振动筛整体有限元模型

图2 主梁位移云图

2 激振器的结构与有限元模型

2.1 激振器几何结构

激振器结构主要由箱体、轴、偏心块、配重、轴承、万向压盖、轴承压盖、甩油盘、迷宫环等组成，如图3所示。

图3 激振器三维模型

2.2 有限元模型

在建立激振器有限元模型时，按如下处理：(1)由于万向压盖、轴承压盖和迷宫环不属于承力件，故在建模时将其忽略。(2)激振器结构上对激振器刚度影响很小的倒角和螺栓孔，建模时也将其忽略。偏心块和配重用螺栓连接，所以将其按照一个整体处理，统称为偏心块。最后激振器简化为箱体、轴、偏心块和轴承四个部分。因为轴承为标准件，不是激振器强度分析的重点；加之轴承结构复杂，若按实际结构离散化，其有限元模型太大，分析困难，所以采用虚拟轴承来模拟；因轴承的滚子与内外圈之间有空隙，刚性比激振器要小，故在计算时，虚拟轴承的弹性模量按比激振器小一个数量级来处理；根据轴承的总质量不变的原则，虚拟轴承的密度取ρ=6.45×103kg/m3。激振器组件材料属性如表1所示。

采用计算精度高的六面体单元对激振器进行离散化。由于激振器结构复杂，实体模型不经过处理很难完全用六面体离散化，所以首先要经过复杂的前处理将激振器进行合理的切分，以保证切分后各部分相对的面结构相似，然后再进行离散化。轴承和轴、轴承和座孔之间是装配结构，其之间的相互作用用接触单元模拟装配。整个结构离散化后单元总数138742，节点总数153624，有限元模型如图4所示。

表1 激振器组件材料属性

图4 激振器有限元模型

3 位移边界条件的确定

激振器底座通过螺栓与振动筛主梁相连接，在对激振器进行有限元强度分析之前，必须先确定其位移边界条件。由于激振器与主梁之间由高强度螺栓连接在一起，故要把前面计算出的整体振动筛主梁的位移赋值给与其相接触的激振器箱体底座底面上。这种位移边界条件的处理会涉及到如下三个问题：(1)振动筛主梁采用板单元模拟，故要将单元中面的位移转化成板顶面的位移；(2)激振器和振动筛模型是在不同坐标系下建立，因此在位移转换时要做坐标变换计算；(3)因为振动筛主梁和激振器底座离散化不同，故各自表面节点不一致，所以要用插值才能计算出激振器底座底面的节点位移。这三点是研究位移边界条件的难点。限于论文的篇幅，下面只对第3个问题计算方法作以说明。

3.1 插值点位置的判定

由于主梁和激振器底座离散化方法不同，故各自表面的节点不一致。为了用与激振器底座相接处的主梁板单元的节点位移插值计算出激振器底座底面上的节点位移，首先要判别激振器底面上节点相对于主梁板单元的位置。模拟振动筛主梁的单元为四边形板单元，如图5所示；和少量退化的三角形板单元，如图6所示。若单元是退化的三角形板单元，则节点3和4重合，其面积Δ134=0和Δ345=0，则激振器底面节点5与两种单元的关系如图5和图6所示。

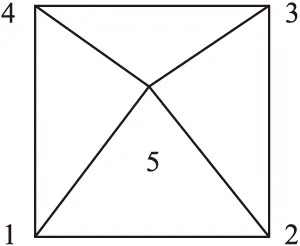
图5 四边形单元

图6 三角形单元

当Δ125+Δ235+Δ345+Δ145=Δ123+Δ134

(1)

等式成立，说明激振器底面节点5位于该单元之内；否则激振器底面节点5位于该单元之外。

3.2 插值点的位移计算

当激振器底面节点5位于四边形单元之内时，则节点5的位移按下式计算。

(2)

式中：ui为单元节点x方向的位移；vi为单元节点y方向的位移；wi为单元z方向的位移；Ni是四边形单元的形函数，

(3)

其中节点5的局部坐标ξ和η可以按照坐标插值公式

(4)

反求出来。

当激振器底面节点5位于三角形单元之内时，则节点5的位移为

(5)

式中：Nj为三角形单元的形函数

(6)

式中,Δj为面积坐标，当j=1时Δ1=Δ235；Δ为三角形单元123的面积(Δ=Δ123)。

用APDL语言编写相应的计算程序，首先读取主梁上相关节点的位移，根据弹性力学薄板理论计算出主梁顶面的节点位移；然后把主梁顶面的节点位移变换到激振器模型的坐标系下；最后通过插值计算可得到激振器底座底面上的各节点位移。程序流程如图7所示。Nnod为激振器底面节点数，EI为主梁最小单元号，Nd为激振器底面最小节点号，F为判定激振器底面节点是否与主梁单元相关联的判定方法。

F=Δ125+Δ235+Δ345+Δ145-Δ123-Δ134

(7)

S为判定与激振器底面节点相关联的单元是四边形还是三角形的判定方法，如图5所示，提取四边形单元的四个节点坐标，若3与4坐标重合则判定该单元是三角形单元，如图6所示。

3.3 载荷

激振器偏心块额定转速为800r/s，故要在偏心块施加相应的离心力。旋转角速度为

(8)

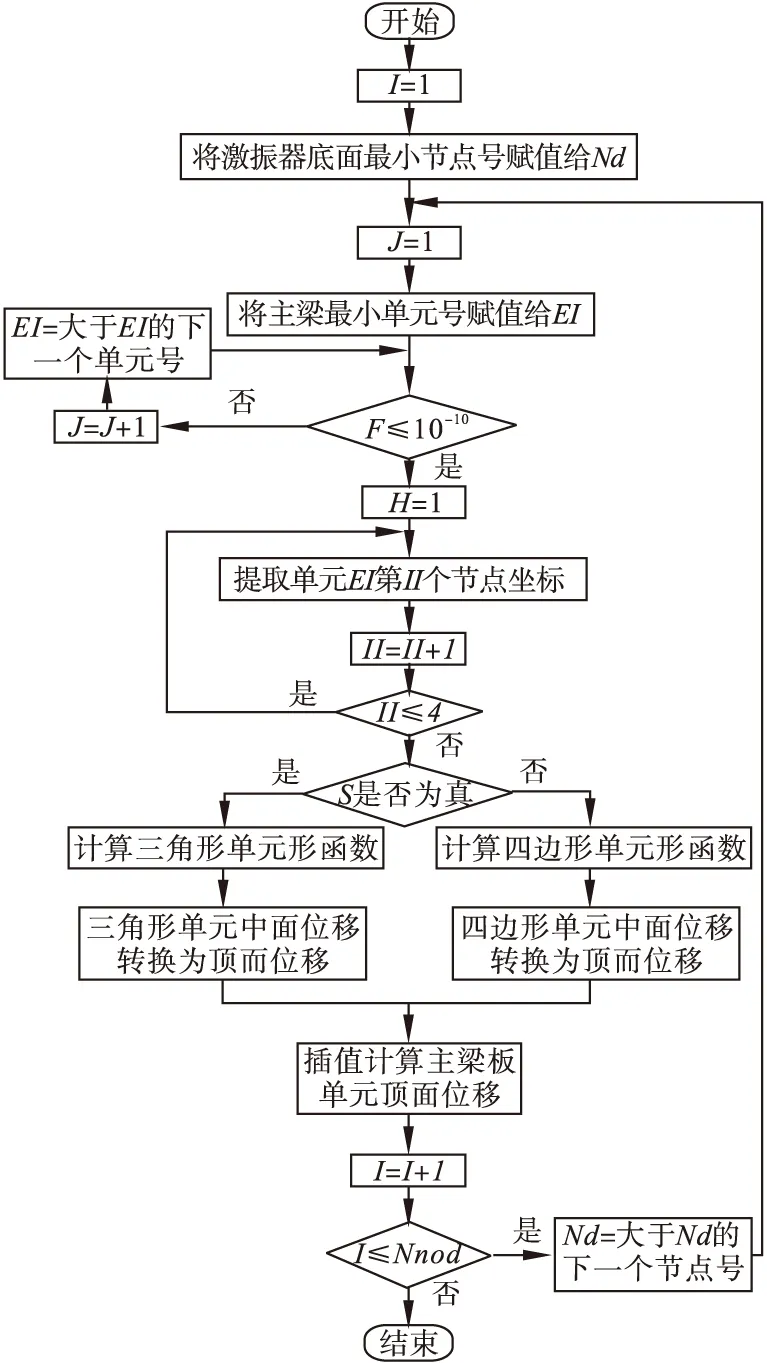
图7 程序流程图注：I、J为循环标记

4 计算结果

4.1 激振器各部件计算结果分析

激振器箱体等效应力如图8所示。由计算结果可见，激振器箱体最大等效应力在其底面与主梁螺栓连接处，其值为42MPa；激振器螺栓分布成8列、2行，最大等效应力点位于从后挡板算起第2列，靠近主梁的中部处。因为激振器与振动筛箱体是用螺栓相连，其激励由螺栓传递给振动筛箱体，所以连接螺栓要承受很大的载荷，故该位置有较大的应力是合理的。

轴的最大等效应力发生在第一个轴肩处，如图9所示，最大等效应力为74MPa。因为由于激振器偏心块旋转所产生的激振力是靠轴和轴承的接触、轴承和箱体的接触传到箱体上的，所以轴上有较大的应力。

图9 轴等效应力云图

偏心块最大等效应力发生在轴与偏心块连接处，为26MPa，如图10所示。与激振器箱体和主轴相比较，偏心块上的应力较小。

图10 偏心块等效应力云图

由于振动筛是振动机械，故取设计安全系数n=4.5[7]。许用应力为

[σ]=σs/n

(9)

各部件最大等效应力、许用应力见表2。

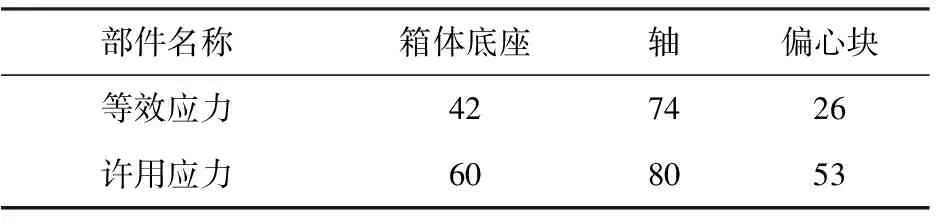
表2 各部件最大等效应力及许用应力 MPa

从表中比较出各部件最大等效应力均小于许用应力，满足强度要求。

4.2 激振器箱体子模型分析

由计算结果可见，激振器底座的最大等效应力接近其许用应力。故为仔细研究激振器底座的应力分布，应用子模型技术，在激振器底座最大等效应力位置，截取以螺栓为中心宽80mm、长100mm的实体进一步细化网格，分析该位置的应力情况。该实体共2560个单元，3213个节点。有限元子模型如图11所示。等效应力如图12所示，其最大等效应力为50MPa。应力分布以螺栓位置处为中心向四周方向分布，等效应力逐渐减小。

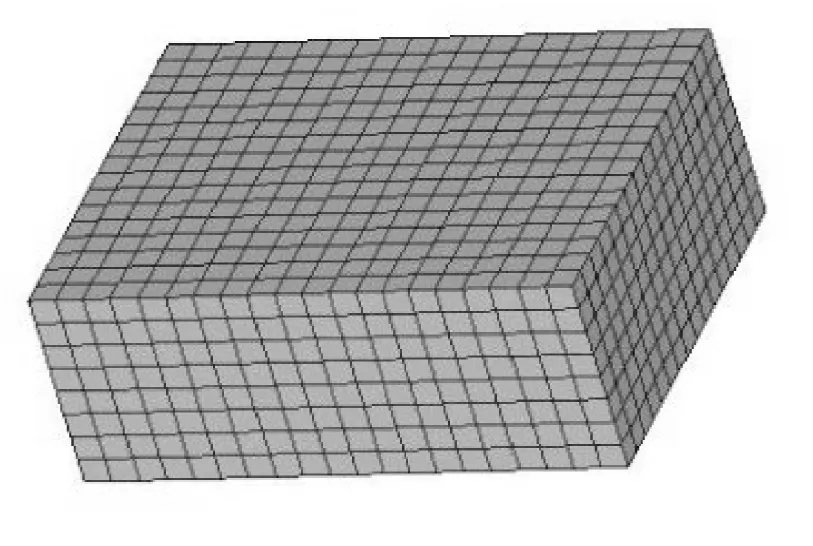
图11 有限元子模型

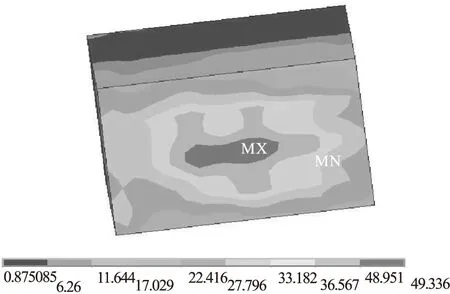
图12 子模型等效应力

5 结论

(1) 通过对振动筛整体进行静力学分析，得出了振动筛筛箱的位移分布，为激振器进行静力分析提供了边界条件的来源。

(2) 根据弹性力学薄板理论计算出主梁顶面的节点位移，通过插值方法确定激振器底面的位移边界条件。

(3) 通过有限元静力分析得出激振器的应力分布。激振器箱体最大应力位于其底座与主梁连接螺栓处，说明了连接螺栓承受着很大的应力，故对螺栓的强度有很高的要求。激振器的主轴在其轴肩处的应力也比较大。

[1]江经华.香蕉形直线振动筛参数化建模与动力学特性分析[D].沈阳:东北大学,2008.

[2]贺孝梅,刘初升,张成勇.基于多频约束和解析灵敏度法的大型振动筛优化设计[J].中南大学学报,2011,42(3):664-670.

[3]杨楚,王新文,朱允进.3661香蕉形直线振动筛结构模态分析[J].选煤技术,2012,(2):20-22.

[4]孙旖.有限元分析在大型振动筛设计中的应用[J].选煤技术,2008,(4):11-14.

[5]冯文婷,任家骏.基于ANSYS的SXK3661型香蕉筛有限元网格划分[J].机械管理开发,2012,(2):194- 195.

[6]赵华,绳飘.振动筛激振器的有限元分析及结构改进[J].煤矿机械,2012,33(5):100-102.

[7]闻邦椿.动态机械的理论与动态设计方法[M].北京:机械工业出版社,2002.

(责任编辑：赵丽琴)

Finite Element Analysis of Intensity of Vibration Exciter of Banana-type Vibrating Screen

AN Xiaowei1,XIE Jiankang1,JI Yujie1,XU Wenbin2

(1.Shenyang Ligong University,Shenyang 110159,China;2.Anshan Heavy&Mining Machinery Industry Co.,Ltd,Anshan 114051,China)

Through the thin plate bending theory,coordinate transformation,displacement transformation and shape function interpolation calculation,determine the displacement boundary condition of the vibration exciter,thus the vibration exciter finite element models is established.Take the finite element analysis of intensity and calculation of the vibration exciter.After taking check of intensity,all parts are in a safe range.

interpolation;finite element;statics;intensity

2014-07-23

安晓卫(1956—)，男，教授，研究方向：机械振动、CAE和结构优化.

1003-1251(2015)04-0034-05

TH237.6

A