一种六关节机器人关节空间轨迹规划方法

董　辉,仲晓帆,黄　胜

(浙江工业大学 信息工程学院，浙江 杭州 310023)

一种六关节机器人关节空间轨迹规划方法

董辉,仲晓帆,黄胜

(浙江工业大学 信息工程学院，浙江 杭州 310023)

摘要：为提高六关节机器人运动效率，保证在最优时间内平滑地完成运动任务，提出一种关节空间轨迹规划方法.该轨迹规划方法首先通过D-H参数法，对机器人进行建模；在末端执行器轨迹上寻找若干个特征点，并通过逆运动学解得六个关节的关节角；采用5次非均匀B样条曲线定义速度、加速度可控的关节轨迹，并获得时间最优轨迹规划的非线性运动学约束条件；最后通过改进的粒子群算法求解关于时间最优的运动轨迹.

关键词：轨迹规划;时间最优;样条;关节空间

Trajectory planning method in joint space for 6-DOF robot

DONG Hui, ZHONG Xiaofan, HUANG Shen

(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:A trajectory planning method in joint space for 6-DOF robot which will guarantee to complete the motion tasks smoothly within the optimal time and improve the efficiency of the robot motion is proposed in this paper. Firstly, the robot is modeled by using D-H method; then, a number of feature points are found on the end of actuator trajectory. The six joint angles are got through the inverse kinematics; Here, the fifth-order non-uniform b-spline curve is used to define the joint trajectory in which the speed and acceleration can be controlled. Then the non-linear kinematic constraints of the time-optimal trajectory can be obtained. Finally, by using the improved particle swarm optimization, the time-optimal trajectory with non-linear kinematic constraints is solved.

Keywords:trajectory planning; time-optimal; b-spline; joint space

关节空间的轨迹是指机器人每个自由度的位置、速度、加速度的时间历程，它们决定了关节机器人是否能在最优时间内平滑地完成运动任务.因此轨迹规划的研究具有普遍的理论与工程意义.遗传算法、模糊逻辑等优化算法被广泛运用于具有时间最优特性的机器人轨迹规划中[1-2].现有的轨迹规划算法大多通过求解目标函数的最优解，从而实现时间、效率、能量等最优.文献中，Piazzi A等通过区间分析法找到全局加加速度最小的轨迹，但未考虑时间问题[3]；Gasparetto A等通过cubic曲线拟合关节空间轨迹，并用序列二次规划法，找到可通过权重因子平衡选择时间最优或者加加速度最小的轨迹规划，该方法设计巧妙，具有一定参考价值[4]；贾庆轩等利用启发式的A*方法在关节空间内进行路径搜索，通过算例进行点到点路径规划数值仿真[5]，但未考虑效率问题；Constantinescu D等在转矩约束条件下通过三次样条曲线进行规划轨迹得到速度、加速度连续的轨迹[6]，并用可变容差法求解时间最优问题，但三次样条无法控制关节轨迹的加加速度项；胡小平等采用多项式插值和Newton插值相结合的轨迹规划方法[7]，该方法在起始段和终止段采用五次多项式插值，中间段采用Newton插值，可以获得连续的轨迹，但无法满足时间最优要求.朱世强等通过7次非均匀B样条曲线构造关节轨迹，对加加速度的处理放在了约束函数中[8]，但7次非均匀B样条曲线计算相对比较复杂.

综合以上轨迹规划方法，首先根据徳布尔算法构造关节空间加加速度连续的5次非均匀B样条函数Pk(t)，并将时间最优问题表述为关节运动累积时间最小的问题；通过对目标函数求导得到速度、加速度、加加速度关于位置变量的函数表达式，并将非线性运动学约束条件加入到计算控制顶点的过程中；最后根据改进的粒子群算法求解具有非线性约束条件的时间最优问题，得到最优的时间序列.

1构造目标函数

通过次非均匀B样条曲线表示目标函数，样条曲线由若干多项式Ni,k(t)线性组合而成.这些多项式都具有一个相应的控制顶点di作为加权系数.

为构造B样条函数，首先需在笛卡尔空间中的几何路径上寻找n个点.再通过逆运动学求解得到笛卡尔空间中的点对应的各个关节的位置矢量p1,p2,…,pn，此处pi泛指任意关节在第i个点处的关节位置矢量.关节空间中通过次非均匀B样条曲线Pk(t)描述关节轨迹为

(1)

其中基函数Ni,k(t)定义为

(2)

因为样条函数的局域性，在时间段[tl,tl+1)的样条曲线Pk(t)由控制顶点dl-k,dl-k+1,…,dl决定，而与其他控制顶点无关.因此，式(1)可表示为

(3)

由式(2，3)可知：关节空间轨迹规划的时间最优问题是以每个时间段的样条曲线Pk(t)累计执行时间最短为控制目标，从而获得目标函数的n+k-1个控制顶点di.在时间节点序列两边各有k个重节点.假设每个时间段为hi=ti+1-ti，则关于时间最优的问题可描述为寻找满足min∑hi的控制顶点的问题，对应的时间节点ti，有

(4)

2分析运动学约束

2.1边界条件处理

机器人的运动必须满足运动学约束条件，本节假设机器人任意关节的运动学约束条件描述，包括速度v、加速度a，加加速度j约束项.具体约束条件为v≤Vmax,a≤Amax,j≤Jmax.

(5)

容易得到关节速度、加速度以及加加速度的函数表达分别为

(6)

给定速度、加速度的初始值与终止值，再代入式(7)，可得各个关节的起始和终止速度、加速度、加加速度，从而实现对边界条件的处理.其中d1,d2,d3,dn+k-3,dn+k-2,dn+k-1，以及由式(3)求解n+k-1个控制顶点.对于六关节机器人系统，以上方程组可由矩阵形式表达，则各个关节的控制顶点可表示为

Ad=P

(7)

其中：P泛指各个关节空间的关节角序列以及关节启停速度、加速度、加加速度组成的序列；A为Rn+5n+5的方阵；d为各个关节空间的控制顶点序列.

通过矩阵运算可得到各个关节空间的控制顶点序列为

d=A-1P

(8)

其中方阵A中元素确定可以表示为

A(i+4,i+j+2)=Ni+j+2,5(ui+3)

(9)

式中：i=0,1,…,n-3；j=0,1,…,k-1.其他行元素根据关节启停速度、加速度、加加速度确定，即实现对边界条件的处理.

2.2运动学约束条件

根据机器人各个关节的速度、加速度上限，机器人关节空间的六个关节均要满足各自的约束条件，其运动学约束由式(5)表述.因此，该运动学约束可描述为：对于任意一个关节运动轨迹，只需要保证该关节运动速度、加速度、加加速度曲线最大值的绝对值能满足相应关节的约束条件即可.关节空间轨迹规划的时间最优问题的非线性运动学约束可由式(5，7)联合得到，即

(10)

3最优化求解

在满足运动学约束条件下，关节空间具有时间最优化特性的轨迹规划问题数学模型可描述为

(11)

(12)

其中：gr(ti)为复杂函数，可通过式(2，6，9，10)联合求的.

该最优化问题是一个具有非显式非线性约束条件的优化问题，常规最优化方法基本难以求解该类问题.由于粒子群算法(PSO, Particle swarm optimization)计算简单、鲁棒性好、收敛速度快[9-10]，因此在普通PSO算法的基础上进行适当改进，将非线性约束条件加入搜索最优解的过程中，改进后的PSO算法即可用于计算具有非线性约束条件的时间最优平滑轨迹规划问题.

改进思想是结合外点罚函数法和基本粒子群算法，将问题的约束条件和目标函数构造一个新目标函数F(t)=f(t)+max{0,gr(t)},(r=1,2,3).对那些违反约束条件的点给以惩罚，再通过粒子群算法思想将得到的新目标函数求最优解.改进的PSO算法步骤如下：

1) 初始化粒子群参数:设定惯性权值ω=0.3，学习因子c1=1,c2=2，粒子数N=20，最大迭代次数M=20，最优化问题的维数D=n-1等.

2) 根据目标函数和约束条件，确定外点罚函数，得出增广的新目标函数fitness ().将初始时间序列带入计算，并要求计算过程满足运动学约束，再计算每个粒子的适应度.

3) 将每个粒子的适应度值与其历史最好适应度值Pbest进行比较，若当前适应度值更优，则用当前位置更新Pbest.

4) 将每个粒子适应度值与整个粒子群所经历的全局历史最好适应度值作比较，如果这个位置比全局历史最优更好，则用当前位置更新gbest.

5) 粒子的速度、位置更新公式分别为

v(t+1)=ωv(t)+c1rand(Pbest-x(t))+

c2rand(gbest-x(t))

x(t+1)=x(t)+v(t)

6) 若达到停止条件，算法停止，返回目标函数取最小值时的自变量的值及目标函数最小值作为解输出；否则，转步骤2.

在最优化问题求解过程中，为提高求解效率，将速度、加速度、加加速度曲线离散化.根据B样条曲线凸包性，选取各个关节速度、加速度、加加速度曲线的控制顶点作为约束条件的局部最值.因此max{0,gr(t)}可直接从控制顶点处选取.

4实验步骤与分析

为验证通过改进后的粒子群算法计算速度、加速度、加加速度连续的六关节机器人时间最优化轨迹规划方法的可行性，使用MATLAB对六自由度串联关节式机器人RBT-6T/S03S机器人进行仿真.以下实验所取参数来源于该机器人参数，实验步骤如下：

1) 通过逆运动学将笛卡尔空间型值点换算为6个关节空间的关节变量，再通过5次非均匀B样条曲线插补6个关节的轨迹.从而获得6个关节关于时间节点的曲线函数.为方便实验，此处直接给定六个关节的关节变量，关节变量如表1所示.

表1　关节空间各关节角

2) 通过结合了罚函数法的粒子群算法，求解在运动学约束下，步骤2所得到的目标函数的最优化解.运动学约束如表2所示.

表2　运动学约束

3) 将步骤2得到的粒子群寻优的时间节点序列：h1=3.738 9 s，h2=2.966 8 s，h3=3.222 4 s，带入式(2，6，9，10)，得到关于时间节点的关节空间角度规划曲线、速度规划曲线、加速度规划曲线以及加加速度规划曲线，如图1~4所示.

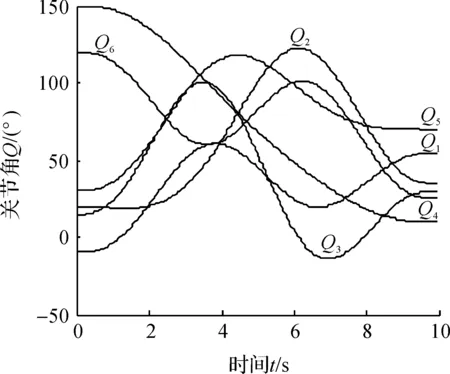
图1　时间最优关节角度规划曲线Fig.1　Time-optimal angle trajectory planning curve

4) 与未使用粒子群优化算法情况下，满足运动学约束的五次B样条曲线轨迹规划结果做比较，如图5所示关节角度轨迹规划曲线图.

由以上实验结果可知：通过改进的粒子群算法获得了最优化时间序列，从而求解得到的关节空间角度、速度、加速度以及加加速度轨迹曲线均连续、平滑，并且满足表2所示的运动学约束条件.

图2　时间最优关节角速度轨迹规划曲线Fig.2　Time-optimal angle velocity trajectory planning curve

图3　时间最优关节角加速度轨迹规划曲线Fig.3　Time-optimal angle acceleration trajectory planning curve

图4　时间最优关节角加加速度轨迹规划曲线Fig.4　Time-optimal angle jerk trajectory planning curve

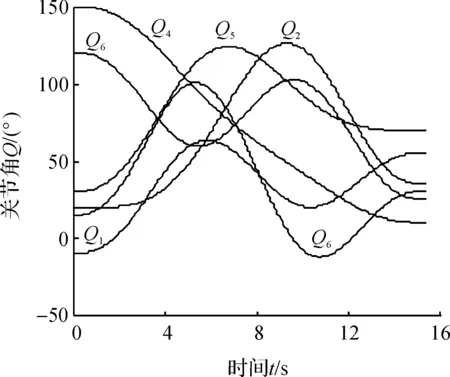
图5　普通关节角度规划曲线Fig.5　Normal angle trajectory planning curve

5结论

在5次非均匀B样条曲线插值的基础上，利用改进的粒子群算法进行轨迹优化，使得六关节机器人在保证速度、加速度及加加速度都在约束范围之内光滑变化的前提下，实现最短时间轨迹规划.利用MATLAB进行轨迹仿真，仿真结果表明：基于粒子群算法的轨迹规划保证了机器人运动时间节点的最优化，而5次非均匀B样条曲线保证了关节角度、速度、加速度的连续性和平滑性，两者的结合得到了六关节机器人关节空间的最优轨迹.

参考文献：

[1]JOHN J CRAIG.机器人学导论[M].贠超,译.3版.北京:机械工业出版社,2010.

[2]董辉,黄文嘉.变增益反馈D型迭代学习控制系统分析与仿真[J].浙江工业大学学报,2014,42(2):214-218.

[3]PIAZZI A, VISIOLI A. Global minimum-jerk trajectory planning of robot manipulators[J]. Industrial Electronics, IEEE Transactions on,2000,47(1):140-149.

[4]GASPARETTO A, ZANOTTO V. Optimal trajectory planning for industrial robots[J]. Advances in Engineering Software,2010,41(4):548-556.

[5]贾庆轩,陈钢,孙汉旭,等.基于A*算法的空间机械臂避障路径规划明[J].机械工程学报,20l0,46(13):109-115.

[6]COSTANTINESCU D, CROFT E A. Smooth and time-optimal trajectory planning for industrial manipulators along specified paths[J]. Journal of Robotic Systems,2000,17(5):233-249.

[7]胡小平,彭涛.一种基于多项式和Newton插值法的机械手轨迹规划方法[J].中国机械工程,2012,23(24):2946-2949.

[8]朱世强,刘松国.机械手时间最优脉动连续轨迹规划算法[J].机械工程学报,2010,43(3):47-52.

[9]KENNEDY J, EBERHART R. Particle swarm optimization[C]//IEEE International Conference on Neural Networks. Piscataway: IEEE Service Center,1995:1942-1948.

[10]HUANG P, XU Y. Pso-based time-optimal trajectory planning for space robot with dynamic constraints[C]// IEEE International Conference on Robotics and Biomimetics. Kunming: IEEE,2006:1402-1407.

(责任编辑：刘岩)

中图分类号：TP242.2

文献标志码：A

文章编号：1006-4303(2015)03-0336-04

作者简介：董辉(1979—)，男，浙江永康人，副教授，研究方向为嵌人式系统技术，E-mail:hdong@zjut.edu.cn.

收稿日期：2014-12-15