一类三次均匀B样条曲线曲面

姚 兴，杭后俊，李晴晴，尹天乐

(安徽师范大学 数学计算机科学学院，安徽 芜湖 241000)

0 引 言

B样条方法不仅保留了Bezier方法的优良性质，而且克服了Bezier方法在形状调节时不具有局部性的缺陷，在参数连续性的基础上完美解决了在描述复杂形状时遇到的连接问题，并将Bezier方法作为其一个特例。此外，B样条方法还提供了一系列配套技术，展示了其在表示和设计自由曲线曲面时的强大能力[1-4]。虽然NURBS方法提供了用权因子来调节曲线曲面的形状[5-6]，但权因子难以驾驭的特点使得一般用户望而兴叹。而实际上，(非有理)B样条方法对于自由曲线曲面形状的表示、设计已经足够，只有在遇到二次圆锥曲线曲面等特殊情况时才考虑使用NURBS方法[7]。但同时也看到，B样条方法也存在自身的缺陷，如只能通过移动控制点来调节曲线曲面形状[8-9]，调节手段过于单一，等等。而由于形状参数的调整更为直观和灵活,因而成为工程应用中用来调节曲线曲面形状的实用方法。因此，国内外学者普遍采用在B样条基函数中引入形状参数的方法[10-15]，但扩展对象主要针对B样条曲线，对将形状参数引入B样条曲面的表示以及对B样条曲面的调节作用讨论较少。

文中首先引入带形状参数的类三次均匀B样条基函数，分析了其基本性质以及形状参数的几何意义；其次基于该组基函数定义了带形状参数的均匀B样条曲线，阐述了形状参数对均匀B样条曲线的调节功能；最后将形状参数引入到均匀B样条曲面中，详细讨论了带形状参数的均匀B样条曲面的基本性质以及形状参数对曲面的影响，并给出了具体实例。

1 带形状参数的三次均匀B样条

称下列分段三次函数为类三次均匀B样条基函数：

Ni,2(u,α)=

(1)

其中，α(-1≤α≤1)为形状参数；n(i=0,1,…,n)为控制顶点下标上限。

不难看出，类二次均匀B样条基函数具有如下基本性质：

(2)局部支撑性：当-1≤α≤1,i≤u≤i+3时，Ni,2(u,α)≥0。

(3)Ni,2(u,α)=Ni-j,2(u-j,α),j=0,1,…,i。即类三次均匀B样条在定义域内的各个节点区间上都具有相同的形状，且任一节点区间上的类三次均匀B样条都可以由另一节点区间上的类二次均匀B样条经过平移得到，如图1所示。其中α取0.25和-0.25

图1 类三次均匀B样条的平移特性

分别对应实线和虚线。

(4)当α=0时，即退化为二次均匀B样条。

Ni,2(u)=

(2)

形状参数α对样条形状的影响如图2所示。其中α取0,0.5和-0.5分别对应实曲线、长虚线和点画线。可以看到，当α越小，样条形状越向左偏，当α越大，样条形状越向右偏。

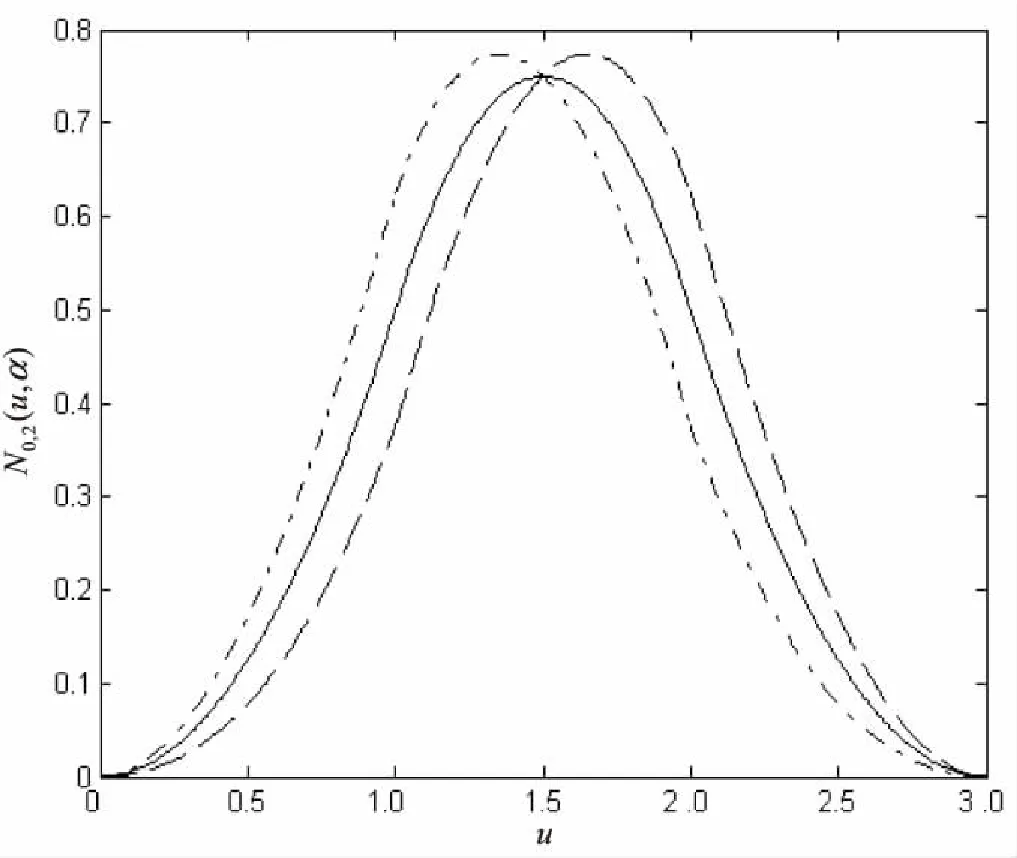
图2 α对样条形状的影响

2 类三次均匀B样条曲线

称曲线Ci(u,α)为类三次均匀B样条曲线。

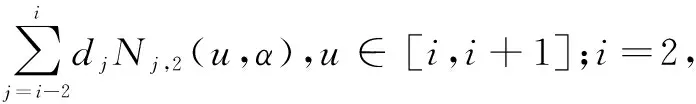
3,…,n

(3)

其中，di(i=0,1,…,n)为控制点；-1≤α≤1为形状参数。

而实际上，只需作参数变换t=u-i，Ni-2,2(u,α),Ni-1,2(u,α),Ni,2(u,α)就可以改写成如下用局部参数的表示形式：

(4)

上述B样条曲线的方程可以表示成如下形式：

Ci(t,α)=di-2B0,2(t,α)+di-1,2B1,2(t,α)+

t∈[0,1];i=2,3,…,n

(5)

类三次均匀B样条曲线具有如下性质：

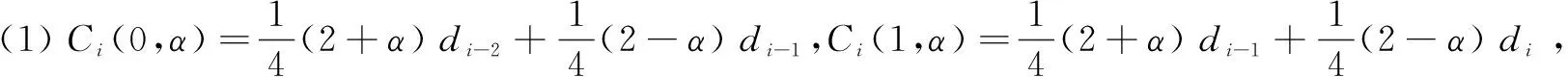
图3表示参数α对曲线Ci(u,α)的影响。

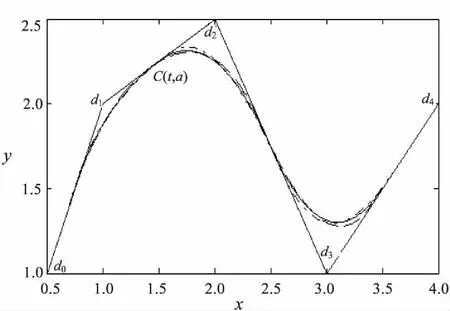
图3 参数α对曲线形状的影响

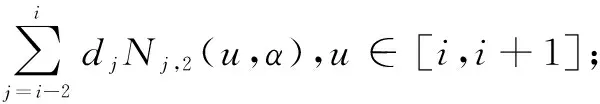
i=2,3,4

(6)

其中，α取0,0.35和-0.35分别对应实线、长虚线和短虚线。

不难发现，在每一节点区间上，当λ越小，曲线越被拉向控制二边形的第一条边；当λ越大，曲线越被拉向控制二边形的最后一条边。

图4为用形状参数表示的均匀B样条曲线形成的一组封闭图形。

图4 类二次均匀B样条曲线形成的封闭图形

3 类3×3次均匀B样条曲面

称如下分片表示的曲面为类3×3次均匀B样条曲面。

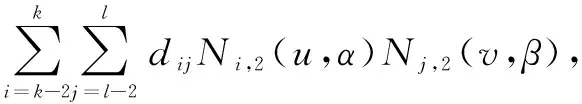
u∈[k,k+1],k=2,3,…,m,

v∈[l,l+1],l=2,3,…,n

(7)

其中，dij(i=0,1,…,m;j=0,1,…,n)为控制点；-1≤α,β≤1为形状参数。

同样，采用局部参数t,s可以表示为如下形式：

l=2,3,…,n

(8)

其中

(9)

(10)

分别取t=0,s=0；t=0，s=1；t=1，s=0；t=1;s=1时，可得曲面片Ckl(t,s,α,β)四个角点的位置。

(11)

α)(2+β)dk-1,l-1+(2-α)(2-

β)dk-1,l]

(12)

(13)

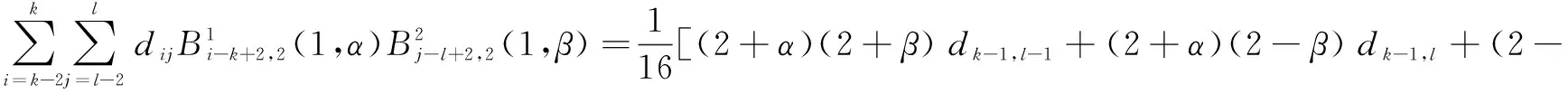
α)(2+β)dk,l-1+(2-α)(2-

β)dk,l]

(14)

可以将角点Ckl(0,0,α,β)写成如下形式：

(15)

其余角点类似。图5为曲面片角点的形成过程。

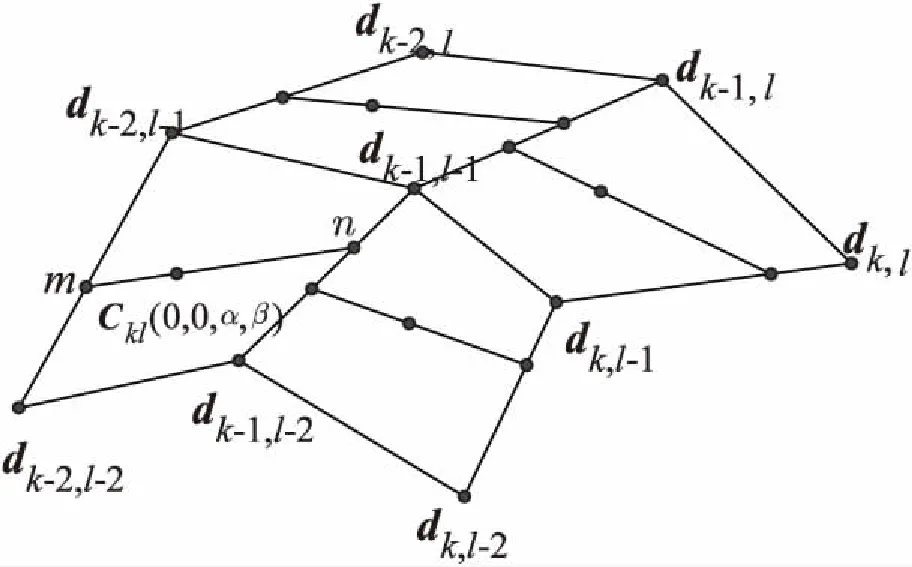
图5 曲面片角点的位置

特别地，分别取k=2,l=2;k=2,l=n;k=m,l=2;k=m,l=n，可得曲面四个角点的位置。

β)d10+(2-α)(2-β)d11]

(16)

β)d1,n-1+(2-α)(2-β)d1,n]

(17)

(18)

(2+α)(2-β)dm-1,n+(2-

α)(2+β)dm,n-1+(2-α)(2-

β)dm,n]

(19)

(20)

其中t,s∈[0,1],k=2,3,…,m,l=2,3,…,n

可以求出

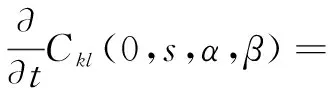
(21)

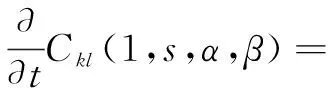
(22)

(23)

同理

(24)

上述结果说明，类3×3次均匀B样条曲面沿等参数曲线跨界G1的。

图6表示参数α，β对曲面形状的影响。左图是α=0.5，β=-0.5时的曲面，右图是α=-0.5，β=0时的曲面。可以看出，在不改变控制点的情况下，通过改变参数α，β的值可达到对曲面形状的调节作用。

图6 参数α，β对曲面形状的影响

4 结束语

通过定义带形状参数的类三次均匀B样条基函数，进而定义类三次均匀B样条曲线与3×3次均匀B样条曲面，不仅保留均匀B样条曲线曲面的原有特点，而且为形状调节增加了额外的手段。由于形状参数的直观易操作，已成为工程应用中设计人员用来调节曲线曲面形状的实用方法。事实上，对于准均匀B样条曲线曲面以及工程中应用更为广泛的两端固支的B样条曲线曲面，也可以寻求相似的扩展方法，使其更加适合工程应用。而更为重要的是，文中方法对于研究非均匀B样条曲线曲面的扩展具有一定的借鉴作用，这将是下一步的主要研究工作。

[1] FARIN G.Curves and surfaces for CAGD[M].5th ed.[s.l.]:Academic Press,2002.

[2] 施法中.计算机辅助几何设计与非均匀有理B样条[M].修订版.北京:高等教育出版社,2013.

[3] 李林峰,马 蕾.三次均匀B样条在工业机器人轨迹规划中的应用研究[J].科学技术与工程,2013,13(13):3621-3625.

[4] AGOSTON M K. Computer graphics and geometric modeling[M].[s.l.]:Springer,2005.

[5] PIEG L.Modifying of the shape of rational B_spline[J].Computer Aided Design,1989,21(8):509-518.

[6] 张国华,杨兴强,张彩明.基于权因子的NURBS曲线形状调整[J].计算机辅助设计与图形学学报,2004,16(10):1396-1400.

[7] 董 枫.船体曲面特征参数化设计技术研究[D].武汉:武汉理工大学,2012.

[8] 张太发,秦新强,程东旭,等.NURBS曲面形状修改的一种改进算法[J].计算机辅助工程,2005,14(4):58-61.

[9] HAN Xuli.Cubic trigonometric polynomial curves with a shape parameter[J].Computer Aided Geometric Design,2004,21(6):535-548.

[10] 陶淑一,吴庆标.基于约束优化的B样条曲线形状修改[J].计算机工程与应用,2006,42(18):37-39.

[11] 谢 进,洪素珍.带形状参数的二次B样条曲线[J].计算机辅助工程,2006,15(2):15-19.

[12] 陶淑一.二次均匀B样条曲线的扩展[J].计算机辅助工程,2008,17(2):54-56.

[13] CAO Juan,WANG Guozhao.Non-uniform B-spline curves with multiple shape parameters[J].Journal of Zhejiang University SCIENCE C:Computer & Electronics,2011,12(10):800-808.

[14] 张 成,熊 建.带双参数的三次均匀B样条曲线[J].吉林师范大学学报:自然科学版,2015,36(2):69-72.

[15] 方 玲,王旭辉.带形状参数的二次非均匀双曲B样条曲线[J].合肥工业大学学报:自然科学版,2016,39(8):1148-1152.