颤振冷挤压振动台设计与振动特性研究
2015-02-18杨庆华王志恒鲍官军
杨庆华,夏 航,王志恒,鲍官军
(浙江工业大学 机械工程学院,浙江 杭州 310014)
颤振冷挤压振动台设计与振动特性研究
杨庆华,夏航,王志恒,鲍官军
(浙江工业大学 机械工程学院,浙江 杭州 310014)
摘要:针对冷挤压成形过程中变形抗力大、易产生挤压不充分的问题,设计了一种新型颤振冷挤压振动台.利用ANSYS软件建立了有限元分析模型,分析确定了振动台安全有效的工作方式,研究了输入油压、振动台加载、弹性端盖凹槽中心半径、弹性端盖凹槽开口高度、弹性端盖凹槽开口圆弧半径等五项振动台振幅影响因素与振幅的数值关系及敏感度,建立了输入-输出的仿真二元插值模型,并通过实验修正模型.实验结果表明:冷挤压过程中振动台振幅共有五个阶段,修正后的模型能有效仿真振动台振幅.研究结果表明:所设计的振动台满足颤振冷挤压成形需要,通过改变振幅影响因素能改善振动台振动特性.
关键词:颤振;冷挤压;有限元分析;二元插值模型;振动特性
中图分类号:TG376.3;TB534+.2
文献标志码:A
文章编号:1006-4303(2015)01-0024-06
Design and research of vibration characteristic of flutter cold
extrusion vibration platform
YANG Qinghua, XIA Hang, WANG Zhiheng, BAO Guanjun
(College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)
Abstract:To reduce the problems of large resistance to deformation and inadequate extrusion, a new flutter vibration platform of cold extrusion was designed. Finite element analysis model was established with ANSYS, the safe and effective working way of the vibration platform was analyzed and determined, the sensitivity and the relationship between five factors of amplitude of the vibration platform such as input oil pressure, loaded on vibration platform, radius of groove center of elastic end cover, groove opening height of elastic end cover, the radius of circular arc groove openings of elastic end cover and amplitude values was researched, the bivariate interpolation model of input-output is established and be validated by experiments. The experimental results indicate that the amplitude of the vibration platform during the cold extrusion process is divided into five phases, and prove that the bivariate interpolation model can simulates amplitude of the vibration platform effectively. Experimental research proves the designed the vibration platform meets the need of flutter cold extrusion forming, and changing amplitude factors can improve vibration characteristics of the vibration platform.
Keywords:flutter; cold extrusion; finite element analysis; bivariate interpolation model; vibration characteristics
冷挤压成形是一种广泛应用于汽车、军工、航空航天、日用五金等各行业的先进金属塑性成形工艺方法,与传统机械加工方式相比,它具有“高效、优质、低消耗、低成本”等优点,是国家的工业化水平及现代化水平的一种重要标志和反映[1].然而,冷挤压零件成形存在很大的变形抗力,成形力巨大,往往需要大吨位的压力机,若成形设备吨位不足,则很容易产生挤压不充分等缺陷[2-3].为解决这一难题,研究人员将振动激励引入塑性成形中,实验证实振动激励能有效降低材料在加工过程的变形抗力[4-6].但是,目前广泛采用的超声振动激励所产生的激振力有限,多用在成形力相对于冷挤压较小的情况下,而用于冷挤压实验的振动挤压多用于易成形“软性”材料做实验,振动台幅值、频率难以精确调整[7-8].因此,设计制造一种适用于冷挤压实验的振动台对改善冷挤压加工工艺有着至关重要的意义.国内对于振动台研究起步相对较晚,在60年代以后,同济大学、哈尔滨工业大学、浙江工业大学等先后对振动台进行了研究,阮健等[9-11]提出的高频电液颤振发生器采用弹性端盖来替代传统活塞实现运动,使得振动发生器频率大为提高,振幅微小,该振动发生器可以用于振动激励挤压.
本研究设计了一种颤振冷挤压振动台,通过对振动台进行静态和动态仿真确定其安全的有效工作方式[12-13];通过单因素分析、敏感度分析和多因素分析研究振动台振动特性影响因素,并进行实验论证[14-16].
1结构设计
为满足冷挤压加工高载荷、小位移的工况,本研究设计的振动台通过激励振动台弹性端盖弹性变形实现颤振,结构图与实物照片如图1所示.振动台采用组合式结构,主要分四大组成部分:顶板、弹性端盖、下板以及密封装置.
顶板的主要作用是将振动台与模具联系起来,其上端与模具的凹模模板固定,下端与弹性端盖连接.弹性端盖外形为带凸台的圆盘,凸台四周设有上下对称的弧状圆环形凹槽,液压油通过油路可进入圆环形凹槽,油的压力直接作用于弹性端盖的下表面,实现弹性端盖绕着圆环形凹槽实现颤振.下板外形为台阶结构,内圈设有凹槽,使得颤振缸体上下板之间存在的一定的间隙.油腔内设有4个扇形加强体,避免弹性端盖在挤压试验的作用下发生过形变导致损坏,加强体隔开四个槽来减小油膜影响,避免液压油不能完全充填油腔.为实现密闭的工作环境,顶出杆套与弹性端盖对应位置设有密封圈,颤振缸体上下板的间隙亦有液压密封胶密封.
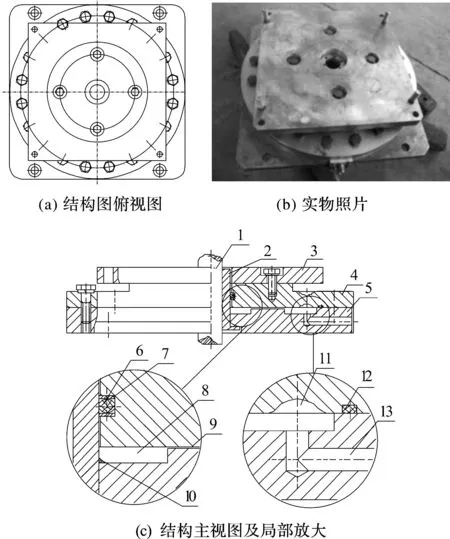
1—顶出杆;2—顶出杆套;3—顶板;4—弹性端盖;5—下板;6—挡圈;7,12—O型圈;8—油腔;9—上下板间隙;10—密封胶;11—弧形凹槽;13—油路图1 颤振冷挤压振动台结构图Fig.1 The structure of flutter cold extrusion vibration platform
振动台采用浙江工业大学阮健教授团队提出的2D激振阀来控制弹性端盖实现上下高频微幅振动.工作时,振动台与2D激振阀、油箱和储能器共同组成颤振冷挤压系统,振动台依靠2D激振阀实现高频微幅振动.通过控制2D激振阀阀芯不断旋转,振动台的弹性端盖将产生微幅振动;通过控制阀芯的旋转运动和轴向位移,能够实现对颤振平台振动频率和幅值的分离控制.
2关键部件仿真分析
2.1静力学分析
弹性端盖作为振动台振动元件,对振动台振动特性有着至关重要的影响,本研究通过静力学和模态分析研究其力学性能.在ANSYS中建模,弹性端盖选用SOLID45单元,材料为60SiMnA,弹性模量E=206 GPa,泊松比μ=0.3,密度ρ=7 850 kg/m3.在弹性端盖内侧受力面施加10 MPa流体压力,分别设置端盖顶部空载和受100 t压力进行计算,由于对称性,采用1/2模型进行仿真,其结果如图2所示.

图2 空载、负载下的等效应力、位移云图Fig.2 The equivalent stress and displacements cloud images under no-load and load
从图2中可以看出:空载和加载下,圆弧槽两端的应力相对较高,在弧形槽外侧过渡节点处出现最大应力,其他部分应力较小,在弹性端盖顶端圆孔附近位移最大.
2.2模态分析
为确定振动台结构与各部件振动状况特性,确定振动台合理的振动频率范围,本研究对振动台进行模态分析[17].对该振动台的有限元模型进行求解运算,并提取其前6阶固有频率和模态振型,如表1和图3所示.模拟时隐藏螺栓等易影响结果的因素,用约束来替代.
表1颤振冷挤压振动台前6阶固有频率
Table 1The first six natural frequencies of flutter cold extrusion vibration platform

数量/阶固有频率/Hz1409.052513.273644.634803.195834.5961075.00

图3 颤振冷挤压振动台前6阶模态振型Fig.3 The first six modal shape of flutter cold extrusion vibration platform
通过分析可知:颤振冷挤压振动台的振动变形主要分为振动台整体的振动变形和振动台顶板的振动变形两类.由振动台前6阶固有频率可得各阶的共振频率,其中1阶固有频率为409.05 Hz,而颤振冷挤压加工过程中,激振器所采用的振动频率在200 Hz以下,实验台固有频率远大于实际实验频率,是一个安全的实验频率,振动台系统不会产生对实验不利共振.因此该装置整体稳定性良好,且各阶固有频率下的变形振幅较小.
3振动特性影响因素分析
3.1单因素分析
颤振冷挤压振动台振动特性关乎冷挤压加工件质量,而输入油压(P)、振动台加载(F)、弹性端盖凹槽中心半径(L)、弹性端盖凹槽开口高度(H)、弹性端盖凹槽开口圆弧半径(r)等因素对振动特性有至关重要的影响,因此需要对这些影响因素其进行分析.振动台振动特性主要包括振幅和频率两部分,根据模态分析,振动台系统固有频率远大于实际实验频率,实验中不会产生对实验不利的共振,动刚度和静刚度基本相同;同时,根据弹性波研究成果可知,该弹性端盖的弹性波传递速度远高于激振速度,在本研究100 Hz的油频条件下,响应频率可认为和激振频率相同.因此,对振动特性的研究主要针对振幅的研究.
设置单因素分析基准,分别改变五个单因素基准的值,控制其余因素为基准值,采用静力学分析研究振动台振幅.基准和影响因素变量如表2所示.

表2 单因素分析基准和影响因素变量表
通过仿真可得各变量和弹性端盖位移的关系曲线,如图4所示.
由图4仿真分析结果可知:弹性端盖位移与输入油压正相关,且近似二元一次函数关系,输入油压6.34 MPa为弹性端盖能否正常激振的临界点;弹性端盖位移与振动台加载负相关,且近似二元一次函数关系,振动台加载111.2 t为弹性端盖能否正常激振的临界点;弹性端盖位移与弹性端盖凹槽中心半径正相关,且近似二元二次函数关系,弹性端盖凹槽中心半径218.1 mm为弹性端盖能否正常激振的临界点;弹性端盖位移与弹性端盖凹槽开口高度、弹性端盖凹槽开口圆弧半径均正相关,且近似二元二次函数关系.

图4 各因素与弹性端盖位移数据拟合图Fig.4 Data fitting map of various factors and elastic cap displacement
3.2敏感度分析
单因素分析描绘了五项影响因素与输出指标的相关性,由以上仿真可见:除振动台加载外其余影响因素与弹性端盖移均为正相关.为进一步对各因素与输出指标的影响程度进行直观地比较,本研究选用正交表L16(45)安排试验,进行敏感度分析.对16组正交试验分别进行仿真分析,并进行极差分析,试验指标是弹性端盖位移,单位为mm,因素—水平和极差结果如表3所示.
根据极差值的大小可以得到因素的主次,从以上极差分析可知,因素的主次为:L>F>P>H>r.
表3正交试验因素—水平和极差分析结果表
Table 3The factor-level table and range analysis results of orthogonal experimental

项目P/MPaF/tL/mmH/mmr/mm因素水平7.25802207177.5852309197.759024011218952501323极差0.052880.068380.073950.026470.01321
3.3多因素分析
通过以上分析可知,在实际冷挤压工作中,随着振动台加载和输入油压的变化,颤振冷挤压振动台振幅也会随之变化,若能控制振动台振幅在振动台加载和输入油压变化的过程中始终处于最优数值区域内则可以有效提高冷挤压工件质量.因此,需对振动台加载和输入油压与振动台弹性端盖的位移之间的数值关系进行多因素分析.结合单因素分析结果,在多因素分析中控制输入油压范围为6~8 MPa,每0.25 MPa设置一个仿真点;控制振动台加载范围为0~40 t,40~80 t,80~120 t三部分,每隔5 t设置一个仿真点.对以上关键点仿真后对数据进行二元插值处理,所得插值图像如图5所示.

图5 输入油压、振动台加载、弹性端盖位移二元插值图Fig.5 The interpolation figure of enter oil pressure, vibration platform load and elastic cap displacement
通过以上多因素分析,建立了输入油压6~8 MPa,振动台加载0~120 t,输出为振动台弹性端盖位移的二元插值图像,研究对得到不同振动台加载和输入油压下的振动台振幅有着重要意义.
4实验研究
整个实验台包含颤振台系统以及检测模块两大部分组成.颤振台系统包括颤振台本体、控制器、2D激振阀、供液油泵、模具等组成,模具通过螺栓连接到颤振台上,颤振台通过液压机台面T型槽固定;检测模块包括激光位移传感器、示波器、加载检测模块.控制器连接激振阀驱动电机,阀体输出连接到颤振台油腔,阀体输入端连接油泵.
该实验目的是为了研究振动台输入条件对振动台弹性端盖振幅的影响,并检验修正前文建立的仿真二元插值模型.第一步,对振动台空载振幅进行分析研究.在振动台轴向不施加载荷的条件下,将振动台输入油液压力设置为5个值,每个值分别检测记录5组振动台弹性端盖振幅波形,分析波形得到振动台位移均值,与二元插值模型仿真模型对比后修正仿真模型,结果如图6所示.计算5组实验比例系数的方差和标准差可知比例系数接近且稳定.因此,为修正仿真二元插值模型,可选取5组实验比例系数均值1.3作为修正系数,即修正后二元插值模型仿真值为原仿真值与修正系数之积.实验证明,经修正后的二元插值模型能较准确仿真振动台弹性端盖在不同激振条件下的振幅,该结果有利于对振动台加载振幅进行进一步分析.

图6 变形量值柱状比较图Fig.6 The columnar comparison chart of deformation magnitude
第二步,对振动台冷挤压过程中振幅进行分析研究.控制振动台输入油液压力为7.5 MPa,油频为100 Hz,完成完整的冷挤压工序,检测记录冷挤压整个过程振动台上表面加载曲线和振动台弹性端盖位移曲线.选取加载曲线关键点后根据修正后的仿真二元插值模型得到振动台弹性端盖仿真位移曲线,与实际检测位移曲线对比研究,结果如图7所示.由图7可见:在冷挤压实验中,挤压初期约0.2 s振动台弹性端盖振幅迅速而平滑地下降;在约0.2~0.6 s时间中振幅伴随剧烈波动进一步下降,但此阶段下降速度明显减缓;在约0.6~1.2 s时间中振幅基本匀速下降至零点,直到在约2.7 s迅速回复至初始振幅.
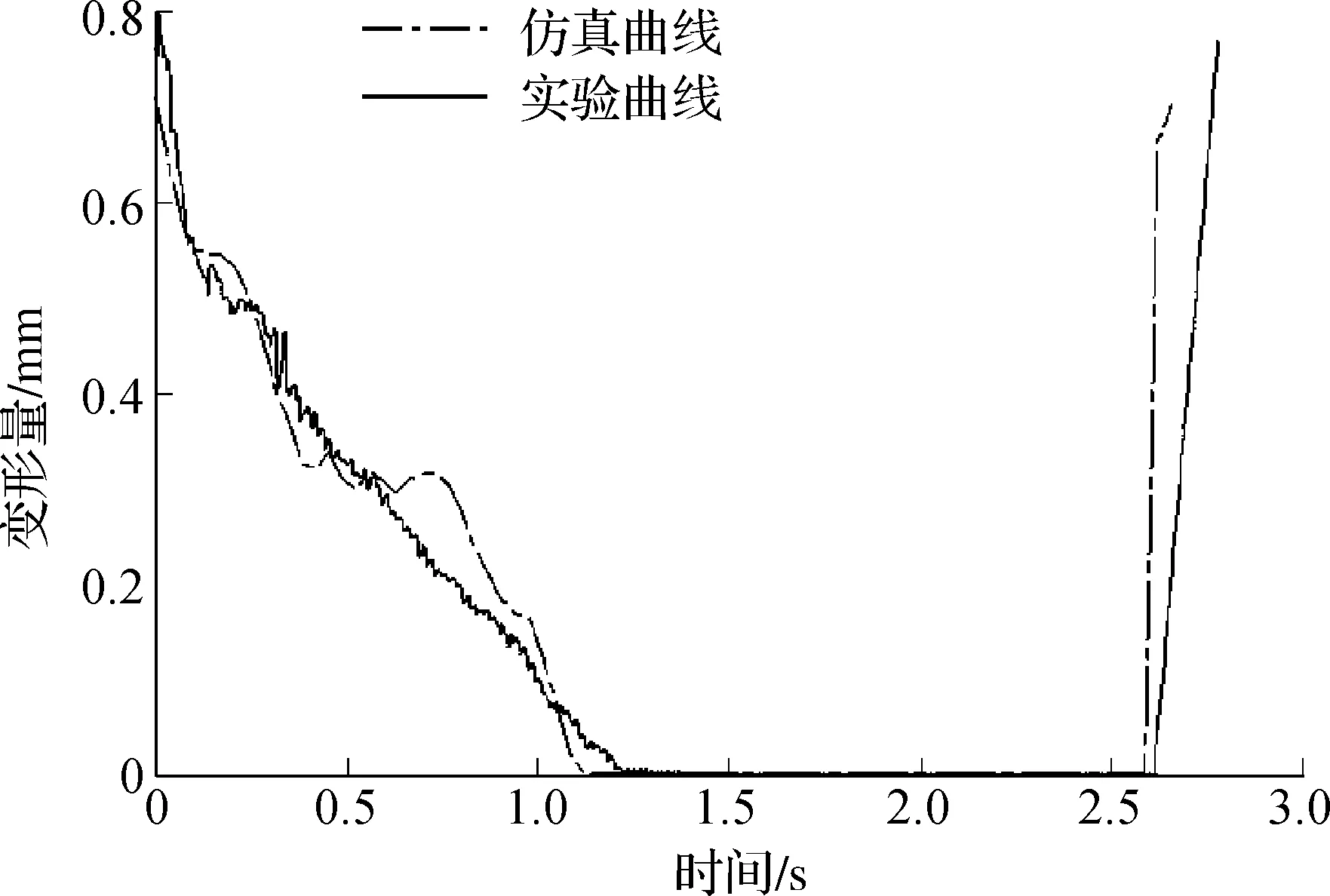
图7 振动台弹性端盖变形量仿真曲线实验曲线比较图Fig.7 The comparison chart of the elastic deformation of the vibration platform cap between experimental curve and simulation curve
对比仿真曲线和实验曲线,两者同样存在振幅前期急速下降阶段、波动阶段、中期急速下降阶段、无法激振阶段和后期回复阶段.虽然两者在各个时间点的数值上有差异,但差异较小,总体曲线走势基本一致.实验证明:仿真曲线能较好反映实际振动台弹性端盖振幅变化曲线,修正后的二元插值模型同样适用于仿真加载条件下振动台振幅.实验结果同时显示了整个冷加压过程中,振动台经历了上述五个激振阶段.
5结论
针对冷挤压成形过程中变形抗力大、易产生挤压不充分的问题,设计了一种新型颤振冷挤压振动台.通过静态和动态仿真校核了所设计振动台的稳定性,运用单因素分析法研究了五项振动特性影响因素与振幅的数值关系,并对比了各因素敏感度,研究数据有利于改善振动台振动特性;通过多因素分析建立了输入为输入油压、振动台加载,输出为振动台弹性端盖位移的二元插值模型,经实验修正后的模型能有效仿真空载和加载下振动台振幅,本研究为控制冷挤压过程中振动台振幅始终处于最优数值范围打下了良好基础.
参考文献:
[1]周贤宾.塑性加工技术的发展—更精、更省、更净[C]//第八届全国塑性加工学术年会论文集.北京:北京航空航天大学板料冲压成形研究中心,2002:1-4.
[2]YAO Zhehe, KIM G Y, FAIDLEY L A, et al. Effects of superimposed high-frequency vibration on deformation of aluminum in micro/meso-scale upsetting[J]. Journal of Materials Processing Technology,2012, 212(3):640-646.
[3]CRISTINA B, GRACIOUS N. Influence of ultrasonic vibration on micro-extrusion[J]. Ultrasonics,2011,51(5):606-616.
[4]何勍,闻邦椿.振动塑性加工的进展及若干问题[J].辽宁工学院学报,1999(4):5-9.
[5]韩清凯,郝建山,闻邦椿.金属材料加工中的振动利用问题[J].中国机械工程,2001,12(5):594-597.
[6]谢涛,齐海群,张俊.超声振动拉丝实验研究[J].中国机械工程,2006,17(3):224-226.
[7]LANGENECKER B. Effects of ultrasound on deformation characteristics of metals[J]. IEEE Transactions on Sonics and Ultrasonics,1996,13:1-8.
[8]MASAO M, MASAHIKO J. The utility of radially and ultrasonically vibrated dies in the wire drawing process[J]. Materials Processing Technology,2001,113:81-86.
[9]韩意斌,俞浙青,阮健,等.新型高频电液激振器[J].液压与气动,2007(7):67-69.
[10]邹正佳,李胜,阮健,等.2D数字伺服阀的动态特性试验研究[J].浙江工业大学学报,2011,39(4):430-432.
[11]邢彤,阮健.高频电液颤振发生器:中国,ZL101858373[P].2010-10-13.
[12]杨庆华,陈鑫,孟彬,等.汽车活塞销振动挤压数值模拟分析[J].浙江工业大学学报,2013,43(3):318-320.
[13]金杰,赵良奎,樊敏娜.喷雾罐顶盖塑性成形过程分析[J].浙江工业大学学报,2012,40(5):584-586.
[14]胡子非,毛华杰.可轴向振动挤压模体精锻过程中振幅影响的数值模拟[J].热加工工艺,2007,36(13):78-81.
[15]张彦敏,张学宾,龚红英,等.有限元在金属塑性成形中的应用[M].北京:化学工业出版社,2010.
[16]陈国兴,左熹,王志华,等.地铁车站结构近远场地震反应特性振动台试验[J].浙江大学学报,2010,44(10):1956-1961.
[17]何文斌,曾攀,林峰,等.40 MN钢丝缠绕多向模锻液压机机架有限元模态分析[J].锻压技术,2011,36(2):18-21.
(责任编辑:刘岩)
作者简介:杨庆华(1964—),男,浙江义乌人,教授,博士,研究方向为金属塑性成形、机器人技术、机电一体化,E-mail:zjutme@163.com.
基金项目:国家自然科学基金资助项目(51275475);浙江省科技厅基金资助项目(2012C21112)
收稿日期:2014-09-05
