考虑摩擦时梁斜碰撞的数值计算

蒲军平，陈　轶

(1.浙江工业大学 建筑工程学院，浙江 杭州 310014；2.浙江省工程结构与防灾减灾技术研究重点实验室，浙江 杭州 310014)

考虑摩擦时梁斜碰撞的数值计算

蒲军平1,2，陈轶1

(1.浙江工业大学 建筑工程学院，浙江 杭州 310014；2.浙江省工程结构与防灾减灾技术研究重点实验室，浙江 杭州 310014)

摘要：基于二维动接触碰撞理论推导出细长梁斜碰撞的数值递推表达式,讨论了不同初始入射角度对斜碰撞的影响,采用Bochet根据钢轨滑动的摩擦系数经验公式,对其中的切向接触模型中的摩擦力做了修正,将计算结果与采用库伦摩擦理论的计算结果做了对比，结果表明：切向摩擦力对法向位移的影响与初始入射角度有关，采用两种不同的摩擦力模型所得到的梁的动力响应结果有明显的差异.

关键词：梁；斜碰撞；摩擦；数值方法

中图分类号：O328; TU311.3

文献标志码：A

文章编号：1006-4303(2015)01-0062-04

Numerical calculation for frictional collision between

an oblique beam and a simply supported beam

PU Junping1,2, CHEN Yi1

(1. College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China；

2. Zhejiang Key Laboratory of Civil Engineering Structures & Disaster Prevention and

Mitigation Technology of Zhejiang Province, Hangzhou 310014, China)

Abstract:The numerical recurrent expression for the collision between an oblique beam and a simply supported beam is presented based on the theory of two-dimensional dynamic contact in the paper. The different angle effects to the beam-beam collision is discussed, an empirical formula of the frictional coefficient, which was presented by Bochet, is accepted to improve the friction in the tangential contact model. Comparing the results between Coulomb friction theory and the improved collision theory, it is shown that the vertical displacement is related to the variable angle and the horizontal friction. Adopting two kinds of different friction models, the dynamic response of the beam is obviously different.

Keywords:beam； oblique collision； friction； numerical method

碰撞接触问题在动力学中的表现为物体在极短时间内的相互作用，运动速度将发生急剧的改变.国内外学者一直尝试给出各类接触问题的解析解，然而这些解析解的求解只能限定于极少数简单且规则的几何体.从20世纪70—80年代初以来，国内外学者的研究成果主要集中在含碰撞的多刚体系统动力学上，Dubowsky针对由于间隙引起的连杆机构的碰撞问题进行了一系列的研究工作[1]，Yigit研究了做大范围回转运动的柔性梁与一刚体碰撞的动力学行为[2],到20世纪80—90年代，国内外学者在建模理论、数值算法等方面做了大量的工作，相继解决了动力刚化、数值病态等方面问题.Wu SC等首次将动态子结构方法应用于柔性杆和梁的碰撞问题[3],Lim等采用有限元方法计算了圆柱体和固定表面的具有摩擦的斜碰撞问题，得到了切向变形和法向变形不协调同步的现象[4].近年来，刘才山，陈滨针对做大范围回转运动柔性梁与固定斜面发生的斜碰撞，利用模态法建立了重力场作用下的柔性梁一致线性动力学方程[5].H.H.Ruan等采用了不同的局部变形模型研究了圆柱体与梁横向碰撞，得到局部变形对整体结构变形的影响[6].沈凌杰等采用绝对节点坐标法结合有限元方法建立了柔性梁的动力学方程，研究了梁点面斜碰撞的问题[7].顾金红等提出了柔性体含摩擦斜碰撞问题的混合分析模型法[8].由上述文献可知：梁作为工程中最基本的构件，对其碰撞问题的深入研究很有意义.笔者在采用二维动接触方法的基础上[9]，借鉴Bochet根据钢轨滑动的摩擦系数经验公式，对二维动接触方法中的切向接触模型中的摩擦力做了修正，探讨了当梁的初始入射角度发生变化时对简支梁的碰撞结果的影响，并进行了数值模拟计算.

1碰撞模型

在实际工程中，许多三维碰撞问题当在忽略平面应变和平面应力时并不显著影响其结果，可以简化为二维碰撞问题来处理.

1.1模型假定

1) 在整个碰撞接触过程中，构件均处于弹性小变形阶段，即忽略接触区域的弹塑性变化对碰撞结果的影响.

2) 构件属于细长杆件,即忽略A梁角点先接触到B梁表面，故可采用梁中性轴碰撞来近似梁碰撞(图1).

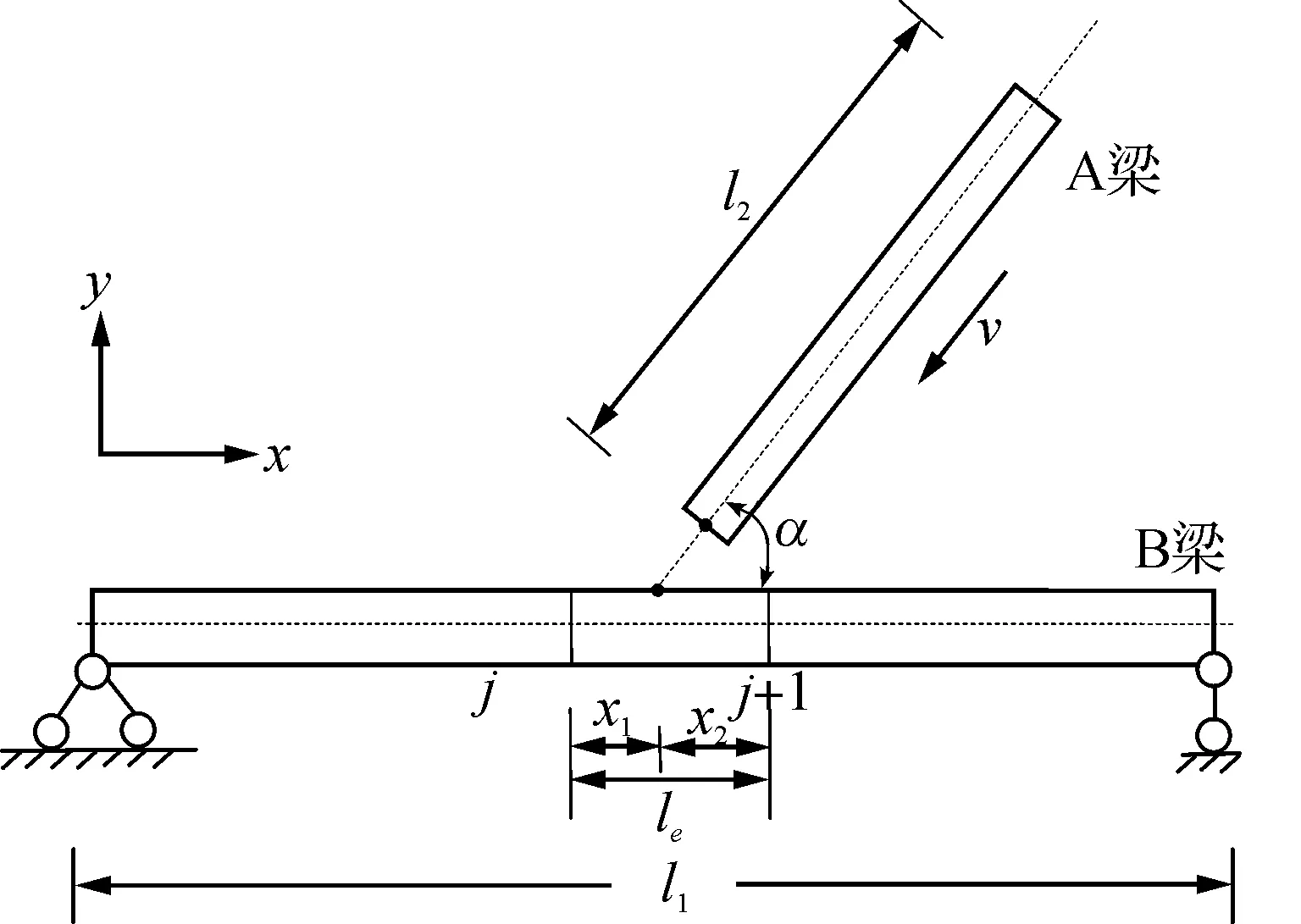
图1　斜梁碰撞模型Fig.1　Collision model of an oblique beam with a simply supported beam

1.2动接触公式推导

梁的动力响应方程为

(1)

其中：M,C和K分别为质量、阻尼和刚度矩阵；U为位移向量；F,R,τ分别为已知的外荷载向量和界面动接触引起的接触法向力和切向力向量.

对于斜向放置的梁在碰撞接触过程中,由于A梁与x方向的夹角随时间不断变化,故协调质量阵与刚度阵等也将不断变化,则将式(1)中的各矩阵向量进行转置(图2).

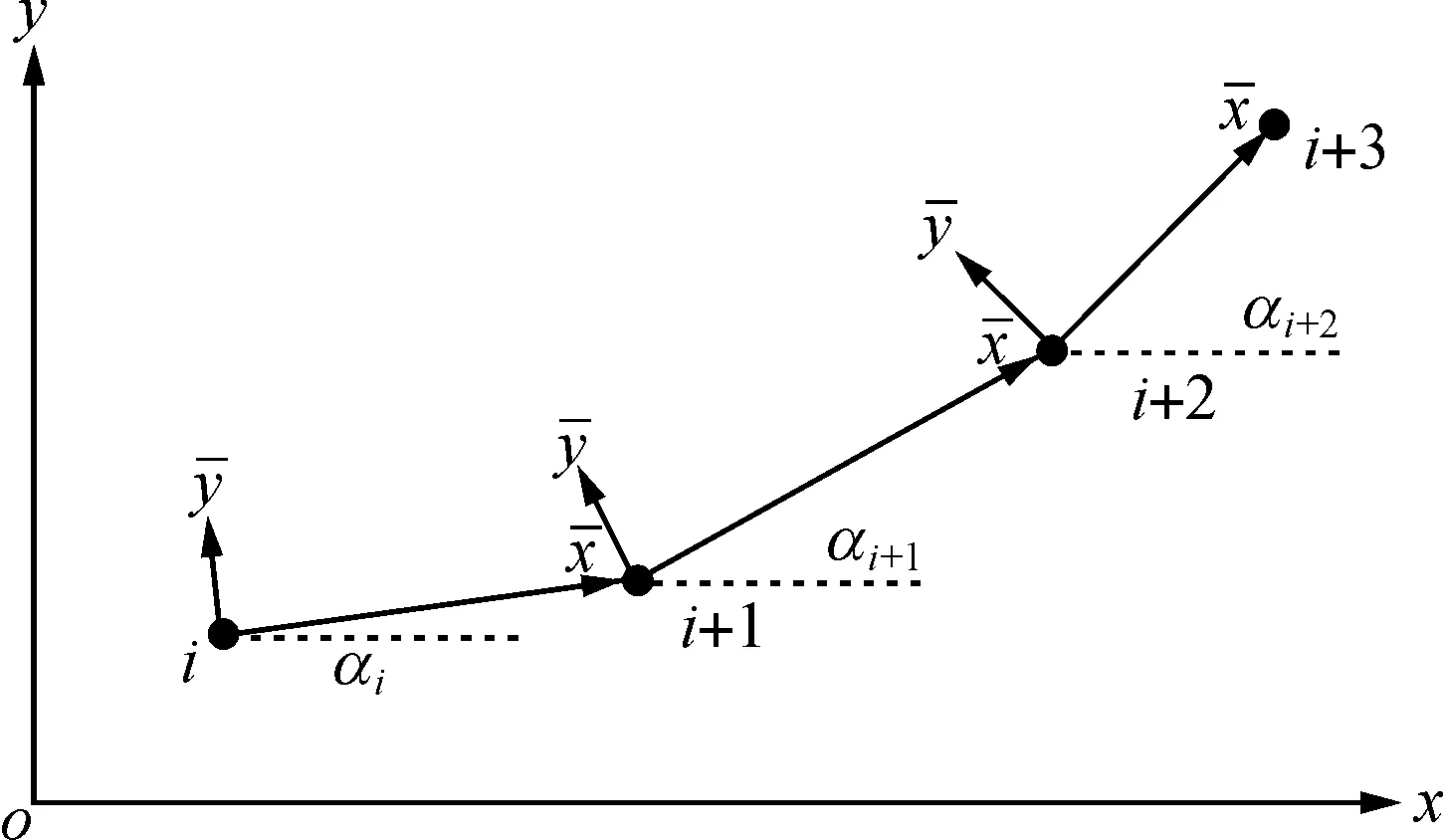
图2　梁中各单元角度变化示意图Fig.2　Angle change sketch map for each element in beam

根据文献[9]针对梁的斜碰撞模型，可得p+1时刻A梁和B梁的位移、速度、碰撞力，其公式分别为

X=A，B

(2)

式中：HA=TM-1(I-(ΔtCM-1)/4)TT； T=diag[T1,T2,…,Ti,…,TN]；M=TMATT；C=TCATT；K=TKATT；F=TFA；τ=TτA；R=TRA；U=TUA.其中:MA, CA, KA, FA, τA,, RA分别为在时变局部坐标系下的物理量；N为A梁的单元数.

i=1,N

在斜碰撞过程中, A梁必将与B梁的j和j+1节点之间的某点发生点对面接触，并记接触点对为(i,i′)(图3).若A梁与B梁的某一节点发生点对点碰撞，则属于点对面碰撞的特殊情况，这里先讨论点对面接触这种一般的情况.

图3　点对面的接触模型Fig.3　Contact model for node to surface

将式(2)应用于A梁和B梁，有

(3)

(4)

式中的H阵和其他各项参数为

HA=

HB=

其中：NA，NB分别为A梁与B梁的总体自由度数目,ξ1=x2/le,ξ2=x1/le.将式(3，4)中接触部分的各项展开，有

(5)

可得碰撞点i′处的切向位移和竖向位移，即

(6)

(7)

1.3关于摩擦系数的修正

当物体间发生斜碰撞时，摩擦对碰撞过程的影响显著，由于接触过程中可能存在粘滑现象，仅采用文献[9]中库伦摩擦理论来分析接触问题显然已经不能满足工程实际的要求，文献[10]也指出了在斜碰撞过程中，摩擦系数具有随着入射角的增大而减小的趋势.文献[11]阐述了影响接触表面摩擦系数的主要因素，给出了表面相对滑动速度是影响动摩擦系数的一个重要因素.笔者借鉴Bochet根据钢轨滑动的摩擦系数经验公式[12]，对其中的切向接触模型中的摩擦力做了如下修正：

(8)

将式(8)回代到式(5)可得到碰撞力R，τ,进而得到某一时刻的位移和速度，然后利用式(2)递推得到整个碰撞接触过程中的位移、速度等物理量.

2算例分析

算例细长梁与一简支梁发生斜向碰撞，如图1所示，B梁表面静摩擦系数取0.35，动摩擦系数取0.25.A梁中点至B梁上表面垂直间距为0.1m，A梁沿轴向以初速v0=5m/s，初始角度α与一简支B梁发生斜向碰撞.A梁为正方形截面，长为2m，截面积为0.01m2，惯性矩为8.3×10-6m4，杨氏模量为E1=6MPa，B梁为矩形截面，截面积为0.02m2，截面惯性矩为，6.67×10-5m4,杨氏模量为E1=6MPa，泊松比为0.47.将A梁划分为4个单元 ,B梁划分为10个单元，时间步长取10-5m.

通过计算，得到不同初始入射角度的梁斜碰撞位移曲线，从图4~6可以看出：A梁与B梁之间发生了多次的碰撞，碰撞节点i的最大法向位移有随着初始入射角度逐渐增大而增大的趋势.在初始角度为60度时, 分别采用变摩擦系数理论和库伦摩擦理论所得到的碰撞节点的动位移曲线有明显的不同，当初始入射角度逐步变化后，两者的动位移差将有逐步减小的趋势.

图4　初始角度为45度Fig.4　The initial angle of 45 degrees

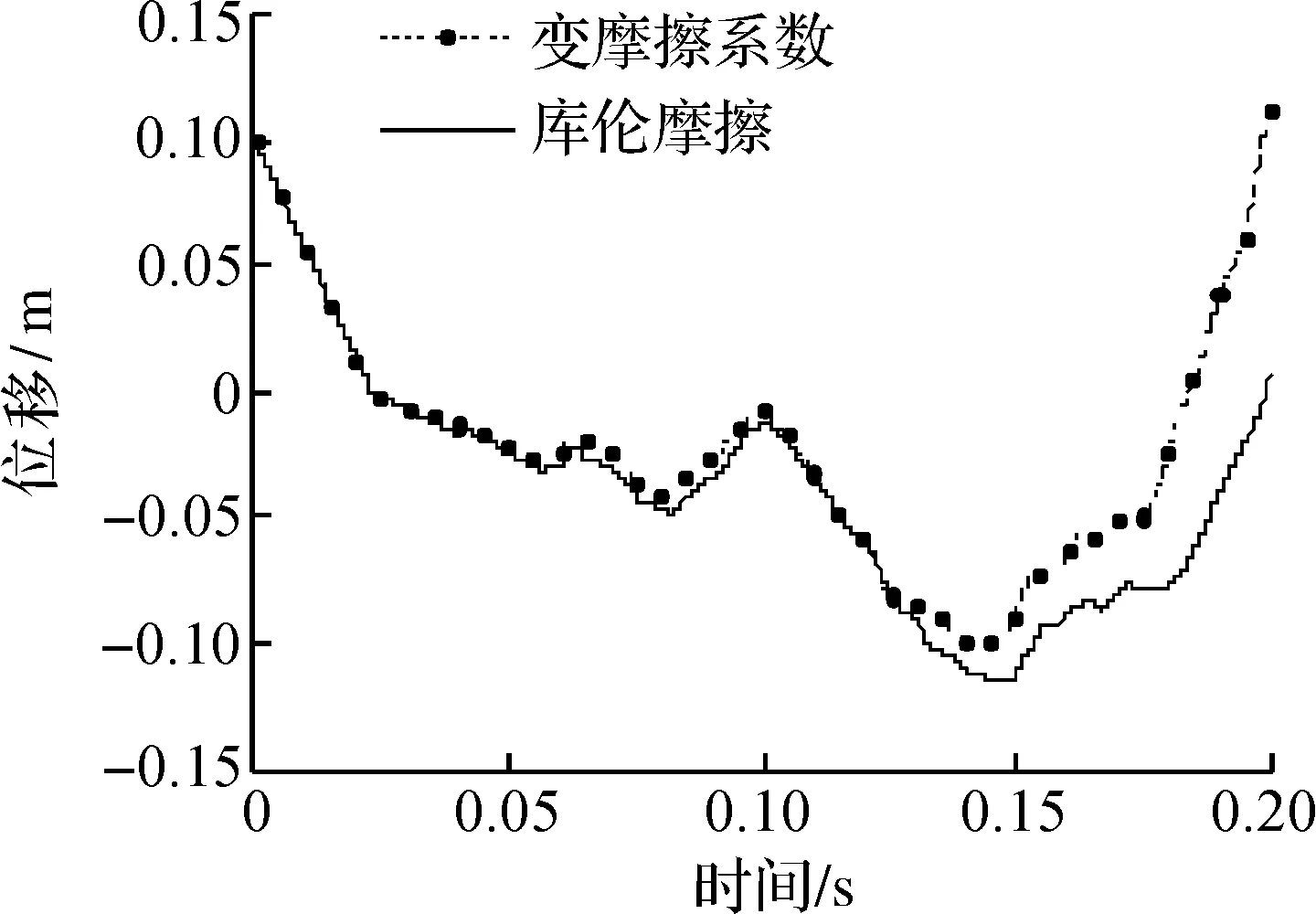
图5　初始角度为60度Fig.5　The initial angle of 60 degrees

图6　初始角度为80度Fig.6　The initial angle of 80 degrees

3结论

通过建立二维梁动接触碰撞动力学方程，对简化后的梁的斜碰撞模型进行了数值计算，研究结果表明切向摩擦对梁碰撞的运动过程有显著的影响.随着初始入射角度不断增大，摩擦力对法向位移的影响也逐步增大.采用库伦摩擦理论与变摩擦系数理论对梁碰撞的过程做了详细的分析，模拟结果显示采用两种不同的摩擦力模型时，随着初始入射角度的递增，碰撞点处的动位移差有先增大后减小的趋势.

参考文献：

[1]DUBOWSKYS，MARKFM.Anexperimentalandanalyticalstudyofimpactforcesinelasticmechanicalsystemswithclearance[J].OriginalResearchArticleMechanismandMachineTheory,1978,13(4):451-465.

[2]YIGITAS,UISOYAG,SCOTTRA.Spring-dashpotmodelsforthedynamicsofaradiallyrotatingbeamwithimpact[J].OriginalResearchArticleJournalofSoundandVibration,1990, 142(3):363-365.

[3]WUSC,HAUGEJ.Asubstructuretechniquefordynamicsofflexiblemechanicalsystemswithcontact-impact[J].JournalofMechanicalDesign,1990,112(3):390-398.

[4]LIMCT,STRONGWJ.Obliqueelastic-plasticimpactbetweenroughcylindersinplanestrain[J].InternationalJournalofEngineeringScience,1999,37(1):97-122.

[5]刘才山,陈滨.作大范围回转运动柔性梁斜碰撞[J].力学学报，2000，32(4):457-464.

[6]RUANHH,YUTX.Localdeformationmodelsinanalyzingbeam-on-beamcollisions[J].InternationalJournalofMechanicalSciences,2003(45):397-423.

[7]沈凌杰,刘锦阳,余征跃.柔性梁斜碰撞问题的非线性动力学建模和实验研究[J].力学季刊，2006,27(4):568-577.

[8]顾金红.柔性体含摩擦斜碰撞问题的混合分析模型法[D].南京：南京理工大学，2014.

[9]刘书.土木工程中动态接触问题的数值计算方法及试验研究[D].北京：清华大学，2000.

[10]吕茂烈.关于斜碰撞时的摩擦系数[J].固体力学学报，1987,3(3):282-284.

[11]林复生,张启浩.滑动摩擦系数的实验室测定法分析[J].广西大学学报:自然科学版，1990,15(3):53-61.

[12]肖乾,林凤涛,王成国，等.变摩擦系数条件下的轮轨滚动接触特性分析[J].铁道学报，2012，34(6):24-28.

(责任编辑：刘岩)

作者简介：蒲军平(1962—)，男，新疆乌鲁木齐人，教授，博士，主要从事固体力学和结构工程研究，E-mail:pjp@zjut.edu.cn.

收稿日期：2014-10-08