反对称铺设的单曲率椭圆形壳结构双稳态性能研究
2015-02-18柴国钟叶钢飞吴化平
柴国钟,叶钢飞,张 征,吴化平
(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室,浙江 杭州 310014)
反对称铺设的单曲率椭圆形壳结构双稳态性能研究
柴国钟,叶钢飞,张征,吴化平
(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室,浙江 杭州 310014)
摘要:通过垂直于圆柱壳方向的圆柱截取反对称铺设的双稳态圆柱壳结构的方法,可得到一种新型的单曲率椭圆形双稳态壳结构,此结构具有伸展和卷曲两种稳定状态.通过最小势能原理对双稳态椭圆形壳结构进行理论研究,得到其卷曲半径理论解,并与有限元模拟结果进行对比来研究不同参数,包括截取半径、圆柱壳的初始半径、铺设层数和铺设角度等对椭圆形壳结构的双稳态特性的影响.在研究双稳态椭圆形壳结构的过程中,通过对截取半径、圆柱壳的初始半径、铺设层数和铺设角度等参数的不同设计,可以得到其不同的双稳态形状,可指导新型的双稳态椭圆形壳结构的制备及应用.
关键词:双稳态;反对称;椭圆形壳结构;有限元模拟
中图分类号:TH123
文献标志码:A
文章编号:1006-4303(2015)01-0001-06
Research on the bistable behavior of the anti-symmetric
singly curved elliptical shell
CHAI Guozhong, YE Gangfei, ZHANG Zheng, WU Huaping
(Key Laboratory of Special Purpose Equipment and Advanced Manufacturing Technology, Ministry of
Education, Zhejiang University of Technology, Hangzhou 310014, China)
Abstract:A new type of bistable elliptical shell can be obtained by cutting out the cylindrical shell by another vertical-direction cylindrical. The new bistable elliptical shell also has two stable states including the extended state and coiled state. The coiled-up radii of the second stable state can be achieved by the minimum potential method in the theoretical analysis. Compared with the results of the numerical simulation, the influencing factors including the cutting out radius, initial mid-plane transverse radius, number of plies and ply angle, are studied on the bistable behavior of the bistable elliptical shell. During research of the bistable elliptical shell, the different shapes of bistable elliptical shell can be achieved from the different design of the cutting out radius, initial mid-plane transverse radius, number of plies and ply angle, which can be used to guide the manufacture and application of the bistable elliptical shell.
Keywords:bistable; anti-symmetric; elliptical shell; numerical simulation
双稳态复合材料结构作为一种新型可变形结构,具有伸展和卷曲两种稳定状态,在外载荷的驱动下可以在两种状态进行转换,并且在不需要外力维持下能够保持在某一稳定状态.这种碳纤维复合材料结构具有质量轻、力学性能优越和空间利用率高等优点[1],在现代飞机机翼结构等场合得到越来越广泛的应用[2].然而,不同的制备方式和铺设方式所得到的双稳态复合材料结构也具有不同形状结构,并且具有不同双稳态特性.采用特殊正交铺设和反对称铺设方式制备的复合材料结构能够获得外轮廓为规则圆柱状的双稳态特性.许多研究者对双稳态特性的研究集中在非对称正交铺设层合板[3-9],这种正交铺设的层合板经过高温固化冷却至室温后,呈现两种稳定的圆柱壳体状态,能够通过集中力或智能材料驱动在两种稳态间转换,并且两种圆柱壳体的曲率方向相反.随着双稳态层合圆柱壳研究的发展,一些人开始研究不同形状的层合圆柱壳结构的双稳态特性.Tawfik等[10]研究了矩形、梯形和三角形正交铺设层合圆柱壳的双稳态特性,通过施加载荷来获取不同几何尺寸对其双稳态特性的影响.Dai等[11]在双稳态层合圆柱壳的基础上,通过不同圆柱壳的组合,实现了多稳态结构.
在反对称铺设双稳态圆柱壳结构的基础上,通过圆柱进行截取,可以得到一种不同于其他形状的双稳态结构——反对称铺设的椭圆形壳结构.通过研究,得到了影响反对称铺设的椭圆形壳结构双稳态性能的几何参数,包括截取半径(r)、圆柱壳的初始半径(R)、铺设层数(n)和铺设角度(α).根据经典层合板理论和最小势能原理,通过理论计算,可以获取椭圆形壳结构第二稳态的曲率半径,并与有限元模拟进行对比,可以得到对椭圆形壳结构双稳态性能影响较大的因素,进而指导相关智能复合材料结构的设计、制备和生产.
1理论分析
椭圆形壳结构相比于其他形状的结构,如三角形、梯形等,结构关于中心对称,且形状规则,具有更广泛的应用领域.Seffen[12]研究了正交铺设的椭圆形壳结构,通过寻找其潜在的稳定状态以及材料参数和初始形状的相关性,来阐述一种新型的可变形结构.Coburn等[13]则研究了双曲率椭圆形壳结构的特性,通过理论预测、有限元模拟和实验验证,得到一种具有三种稳定状态的双曲率椭圆形壳结构.反对称铺设的椭圆形壳结构与正交铺设的椭圆形壳结构有所区别的是其两个稳态的曲率方向一致.反对称铺设的双稳态圆柱壳结构首先是由Daton-Lovett[14]发现并进行研究的,这种反对称层合圆柱壳结构能在伸展和卷曲时都保持稳定.一些学者也开始对反对称层合圆柱壳结构进行一定的理论研究,K. Iqbal和S. Pellegrio[15]基于经典层合板理论率先提出双稳态模型,并得到其应变能表达式.聂国华和顾欣[16-17]对反对称层合圆柱壳结构的力学特性进行了研究,建立了双稳态结构的力学模型.吴耀鹏等[18]建立了存在预应力的各向同性材料圆柱壳的双稳态力学模型,通过对应变能力表达式求极小值法,得到圆柱壳第二稳态的曲率半径.Zhang等[19-21]对规则和非规则铺设的反对称层合圆柱壳结构的双稳态特性进行了理论、模拟和实验研究,并对影响其双稳态特性的多个因素进行了研究和讨论.
在反对称圆柱壳结构的基础上,通过圆柱截取得到反对称椭圆形壳结构在其中一个方向上的曲率为零,则可将模型简化为椭圆形单曲率壳结构问题,如图1所示,其中图1(d)为椭圆形壳结构内部的铺层方式.利用最小势能原理,可以得到势能极小值,即反对称椭圆形壳结构能够保持的稳定状态,通过势能对曲率的求导,可得到椭圆形壳结构达到稳态时的曲率值,用来描述其第二稳态的特性.其中,影响其初始形态以及第二稳态特性的参数可以分为4个参数:r为圆柱截取半径,R为圆柱壳的初始曲率半径(即椭圆形壳结构的初始曲率半径),n为铺设层数,α为铺设角.

图1 反对称铺设的椭圆形壳结构Fig.1 The anti-symmetric elliptical shell
复合材料层合板在外载荷的作用下,可以产生内力和内力矩,由经典层合板理论可得到反对称层合板的物理方程为
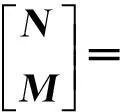
(1)

反对称层合圆柱壳的双稳态性能是由于层合板的拉弯耦合的作用,因此,在椭圆形壳结构的理论研究中,也应考虑弯曲应变能和拉伸应变能.从能量角度分析,反对称椭圆形壳结构的两种稳态对应结构总势能的两个极小值,可通过极小势能法来求解反对称椭圆形壳结构的两个稳态.
单位面积的弯曲应变能表达式[22]为
(2)
将式(1)代入式(2),可以得到总的弯曲应变能式为

(3)
其中B′=-A-1B.
单位面积的拉伸应变能则由下表达式[22]为
(4)
将式(1)代入式(4)得到总的拉伸应变能式为
(5)
由式(3,5)可得总的应变能表达式为
U=Ub+Us
(6)
由于椭圆形壳结构到达第二稳态时,其中一个曲率ky=0,则由极小势能法原理可得第二稳态曲率kx为

(7)
则椭圆形壳结构的第二稳态曲率半径R′为
(8)
2有限元数值模拟
为验证理论计算的结果,采用ABAQUS有限元分析软件对反对称椭圆形壳结构的稳态转换进行模拟,可以得到其第二稳态曲率半径的有限元解和应力分布情况[23].其中建模过程采用一般复合材料壳结构的设置方法,材料为各向异性层合板,材料属性如表1所示,并在CompositeLayup中设置铺层数n和铺设角度α及单层板厚度t.单元采用S4R壳单元类型,中心部分采用四边形规则网格,周围采用扫描自动生成网格,划分为1 280个单元进行分析,如图2所示.其中椭圆形壳结构双稳态转变过程包括两个过程:首先为加载过程,在椭圆形壳结构的四个端点A,B,C,D施加集中力,使其进行稳态转变;之后为卸载过程,撤去4个集中力,椭圆形壳结构将会稳定在第二稳态.由于层合壳结构在稳态转变过程中涉及较大的几何非线性,因此需要开启非线性大变形选项,即Nlgeom设置为on,同时按照默认参数设置Automaticstabilization以使分析结果更易收敛.

表1 椭圆形壳结构单层板的材料属性
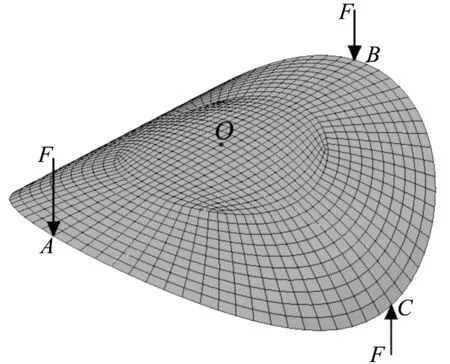
图2 反对称椭圆形壳结构的有限元模型Fig.2 The finite element model of anti-symmetric elliptical shell
通过有限元模拟,在椭圆形四端施加集中载荷,得到反对称椭圆形壳结构的双稳态转变过程,如图3所示,此椭圆形壳结构铺层角度为±45°.从图3中可得:椭圆形壳结构的第二稳态的应力分布为关于中心点反对称分布,最大应力集中在中心区域附近的两个点,即形变受压最大的区域,并且应力大小从中心向外呈递减分布.除此之外,椭圆形壳结构的两个稳态的曲率方向一致,当到达稳定状态时,其中一个曲率恒为零.通过模拟结果可得变形之后所有节点的坐标值,A,B和O的三点组成的截面如图4所示,采用三点坐标求曲率半径的方法计算可以得到第二稳态的曲率半径.到达第二稳态时,A,B和O的坐标已知,可得到AE,OE的长度,则曲率半径为
(10)
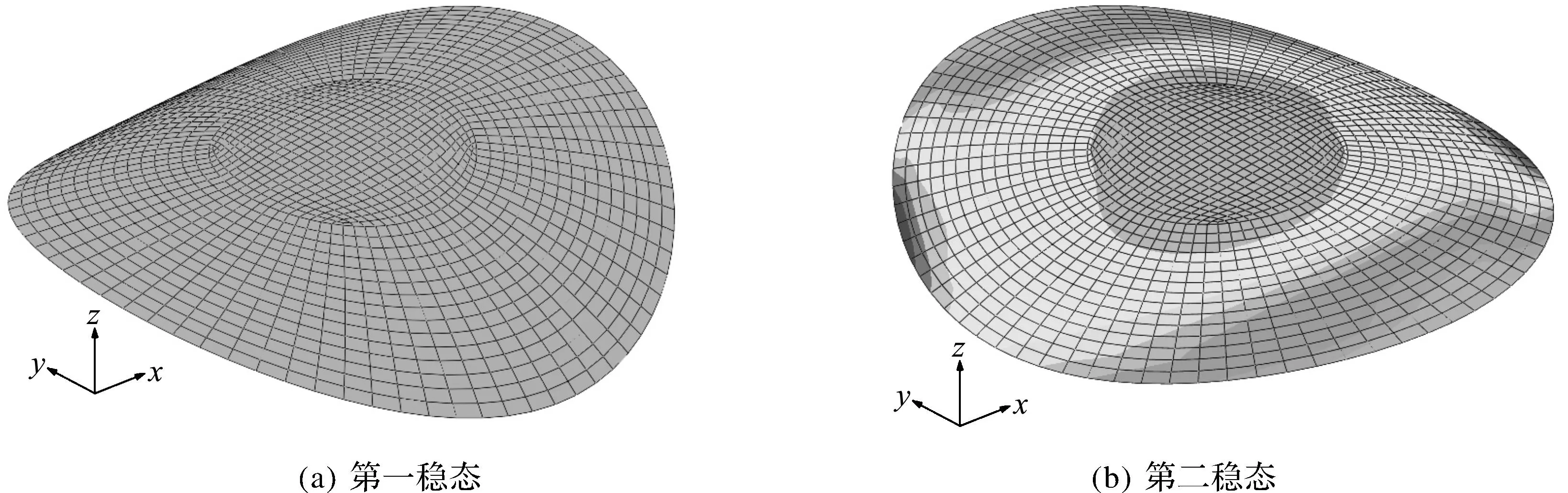
图3 反对称椭圆形壳结构的双稳态的转变Fig.3 The snap process of anti-symmetric elliptical shell

图4 三点坐标求曲率半径法Fig.4 The acquisition of curvature radius by three points
3结果分析

3.1截取半径r的影响结果分析
由于不同的截取半径r对椭圆形壳体的双稳态性能有一定的影响,尤其椭圆形壳体的初始状态的大小由主要由截取半径r决定,因此针对不同的截取半径r进行模拟和理论计算,研究它对第二稳态的影响.其中,保持初始半径R为40 mm、铺层数为5层、铺设角为45°不变,而改变截取半径从20~35 mm的四个试件进行研究,模拟结果如表2所示.理论上,截取半径r对椭圆形壳结构的第二稳态曲率半径Ra′并没有影响;从模拟结果可以发现,随着截取半径r的增加,椭圆形壳结构的第二稳态曲率半径Rf′与理论上得到的结果越来越接近,误差越来越小.尤其当截取半径过小如20 mm时,椭圆形壳结构没有第二稳态,这是由于其第二稳态曲率半径过大,而截取得到的椭圆形壳结构整体尺寸过小,无法使其保持在第二稳态.此外,随着截取半径r的不断增加,椭圆形壳结构的整体尺寸也随之增大,因此所需要使其进行稳态转变的驱动载荷也会随着增加.
表2不同截取半径r的R′理论和模拟结果对比
Table 2The comparison ofR′ with differentr

mm
3.2初始半径R的影响结果分析
为了研究被截取的圆柱壳的初始半径R对椭圆形壳结构双稳态特性的影响,按照初始半径R不同采取4个椭圆形壳结构的试件,模拟结果如表3所示.从理论结果可以看到椭圆形壳结构的第二稳态曲率半径成线性增加,两个稳态的曲率半径的比值保持在一个常数,如图5所示.但是椭圆形壳结构第二稳态曲率半径的模拟结果比理论结果大,并且当初始半径增加到40 mm时,由于椭圆形壳结构第二稳态曲率半径过大无法维持在第二稳态.相对于同一截取半径,不同的初始半径对整体尺寸影响并不明显,当其第二稳态曲率半径变大时稳态转变载荷则会相应减小.随着初始半径的增加,截取半径可选范围也随之增大,这为不同适用场合需求的椭圆形壳结构提供了充分的选择方案.
表3不同初始半径r的R′理论和模拟结果对比
Table 3The comparison ofR′ with differentr

mm

图5 初始半径R对椭圆形壳结构的影响Fig.5 The influence of initial mid-plane transverse radius R on the elliptical shell
3.3铺层数n的影响结果分析
对于不同铺层数n,模拟了4个椭圆形壳结构试件,铺层数为4至7层,得到结果如表4所示.从图6中可以发现:铺层数对椭圆形壳结构的双稳态特性影响并不明显,结果表明不管椭圆形壳结构的铺层数如何变化,第二稳态曲率半径几乎不变.随着铺层数的增加,椭圆形壳结构的厚度也相应增加,导致即使是同一形状的椭圆形壳结构所需的稳态转变载荷也会随着铺层数的增加而增加,因此椭圆形壳结构的内应力也会增加.

表4 不同铺层数n的R′理论和模拟结果对比

图6 铺层数n对椭圆形壳结构的影响Fig.6 The influence of number of layups on the elliptical shell
3.4铺设角度α的影响结果分析
由于复合材料中不同纤维铺设角对整体结构有较大的影响[24],因此根据不同的铺设角度α,选择4个试件进行研究,铺设角分别为40°,45°,50°,55°,通过对比椭圆形壳结构第二稳态曲率半径的理论结果Ra′和模拟结果Rf′,得到结果如表5所示,可以发现理论结果与模拟结果的误差保持在10%以内.椭圆形壳结构的第二稳态曲率半径随着铺设角的增加而减小,如图7所示,即铺设角越大,椭圆形壳结构越弯曲,铺设角小时,椭圆形壳结构越平滑,铺设角对其双稳态特性影响较明显.因此,当需要固定尺寸大小及初始半径时,可以根据不同的铺设角来改变其第二稳态的形状,从而满足所需要求.

图7 铺设角α对椭圆形壳结构的影响Fig.7 The influence of ply angles on the elliptical shell
4结论
理论计算和有限元模拟结果表明:截取半径(r)是影响反对称椭圆形壳结构初始状态的重要因素,能够根据不同的截取半径来改变其初始的尺寸大小,但对其转变到第二稳态的影响较小;初始半径(R)和复合材料层铺设角度(α)对反对称椭圆形壳结构的双稳态性能影响较大,其第二稳态曲率半径随着初始半径的增加而明显增大,但随着铺设角的增大而显著减小;铺设层数(n)只能影响稳态转变时的所需载荷;椭圆形壳结构的两个稳态转变所需的驱动载荷也会随着其初始尺寸和到达第二稳态的曲率半径的变化而变化.根据以上结论,可以根据实际需求来对椭圆形圆柱壳结构进行合理设计,从而指导相应的生产及应用.
参考文献:
[1]LACHENAL X, DAYNES S, WEAVER P M. Review of morphing concepts and materials for wind turbine blade applications[J]. Wind Energy,2013,16(2):283-307.
[2]PONTECORVO M E, BARBARINO S, MURRAY G J, et al. Bistable arches for morphing applications[J]. Journal of Intelligent Material Systems and Structures,2013,24(3):274-286.
[3]HYER M W. Some observations on the cured shape of thin unsymmetric laminates[J]. Journal of Composite Materials,1981,15(2):175-194.
[4]BOWEN C R, BUTLER R, JERVIS R, et al. Morphing and shape control using unsymmetrical composites[J]. Journal of Intelligent Material Systems and Structures,2007,18(1):89-98.
[5]GUDE M, HUFENBACH W, KIRVEL C. Piezoelectrically driven morphing structures based on bistable unsymmetric laminates[J]. Composite Structures,2011,93(2):377-382.
[6]GIGLIOTTI M, MINERVINO M, GRANDIDIER J C, et al. Predicting loss of bifurcation behaviour of 0/90 unsymmetric composite plates subjected to environmental loads[J]. Composite Structures,2012,94(9):2793-2808.
[7]张征,吴和龙,吴化平,等.正交铺设碳纤维复合材料结构的双稳态特性研究[J].功能材料,2013,44(2):236-239.
[8]张晓艳.非对称正交铺层双稳态复合材料的发展与应用[J].航空制造技术,2012(17):70-71.
[9]董文俊,孙秦.不对称铺层复合材料层合板的双稳态机理分析[J].机械科学与技术,2012,31(3):461-464.
[10]TAWFIK S A, STEFAN DANCILA D, ARMANIOS E. Planform effects upon the bistable response of cross-ply composite shells[J]. Composites Part A: Applied Science and Manufacturing,2011,42(7):825-833.
[11]DAI Fuhong, LI Hao, DU Shanyi. A multi-stable lattice structure and its snap-through behavior among multiple states[J]. Composite Structures,2012,97:56-63.
[12]SEFFEN K A. ‘Morphing’ bistable orthotropic elliptical shallow shells[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science,2007,463(2077):67-83.
[13]COBURN B H, PIRRERA A, WEAVER P M, et al. Tristability of an orthotropic doubly curved shell[J]. Composite Structures,2012,96:446-454.
[14]DATON-LOVETT A. An extendible member: UK, PCT/GB97/00839[P]. 1996-01-01.
[15]IQBAL K, PELLEGRINO S, DATON-LOVETT A. Bi-stable composite slit tubes[C]//IUTAM-IASS Symposium on Deployable Structures: Theory and Applications. Netherlands: Springer,2000:153-162.
[16]顾欣.双稳态复合材料结构力学特性的分析[D].上海:同济大学,2004.
[17]聂国华,顾欣.复合材料壳体结构的双稳态特性研究[C]//中国力学学会学术大会.北京:中国力学学会,2005.
[18]吴耀鹏,聂国华.双层壳的双稳态力学特性理论分析和数值模拟[J].力学季刊,2009(3):481-487.
[19]ZHANG Zheng, WU Helong, HE Xiaoqiao, et al. The bistable behaviors of carbon-fibre/epoxy anti-symmetric composite shells[J]. Composites Part B: Engineering,2012,47:190-199.
[20]ZHANG Zheng, WU Helong, WU Huaping, et al. Bistable characteristics of irregular anti-symmetric lay-up composite cylindrical shells[J]. International Journal of Structural Stability and Dynamics,2013,13(6):1350029.
[21]ZHANG Zheng, WU Huaping, YE Gangfei, et al. Systematic experimental and numerical study of bistable snap processes for anti-symmetric cylindrical shells[J]. Composite Structures,2014,112:368-377.
[22]MANSFIELD E H. The bending and stretching of plates[M]. Second Edition. Cambridge: Cambridge University Press,1989.
[23]张征,吴化平,鲍雨梅,等.基于自适应无网格的HA-Ti梯度材料接触分析[J].浙江工业大学学报,2013,41(2):210-213,227.
[24]杨俊杰,周涛.纤维铺设角度对FRP-混凝土组合柱承载力影响的有限元分析[J].浙江工业大学学报,2014,43(3):294-297.
(责任编辑:刘岩)
作者简介:柴国钟(1957—),男,浙江杭州人,教授,博士生导师,研究方向为机械强度及计算机辅助工程、先进模具技术,E-mail:Chaigz@zjut.edu.cn.
基金项目:国家自然科学基金资助项目(51205355,11372280);教育部高等学校博士学科点专项科研基金资助项目(20123317120003);中国博士后科学基金资助项目(2013M540498)
收稿日期:2014-09-25
