海底管线整体屈曲过程中土体水平向阻力模型研究

刘 润，刘文彬, ，洪兆徽，王 乐

（1.天津大学 水利工程仿真与安全国家重点试验室，天津 300072；2.中交天津港湾工程研究院有限公司，天津 300222）

1 引 言

海底管线在使用时受到高温、高压的联合作用，由于地基土体对管线的约束作用，管线无法自由变形，因此管壁内累积较大的附加应力，当累积的附加应力超过土体对管线的阻力时管线发生整体屈曲，由此可见，地基土体对管线的约束是导致管线发生整体屈曲的重要因素，影响着管线发生屈曲变形的条件和变形发展的规律性。

土体对管线阻力的研究较早见于1973年，Lyons[1]在砂土和软黏土中进行了管线水平向滑动试验，试验结果显示，在砂土中管线与砂土之间的摩擦系数为一常量，在黏土中这一摩擦系数不为常数，而是随着管径、管线沉陷量、土的浮重度的增加而增大。Brennodden 等[2]在硬黏土、粉质松散细砂、软黏土和中粗砂4 种土体中对不埋管线水平向运动时所受阻力进行了试验，并得出了相应的土体阻力系数[2]。Bruton 等[3]进行了低剪切强度/低渗透率的软黏土在水平向循环荷载作用下的管-土相互作用试验，试验结果表明，在管线水平运动过程中，管线前部会出现较高的土拱，土体对管线的水平阻力迅速升高，库仑摩擦模型已不适用。Bruton 等[4]研究了管线发生水平向整体屈曲时受到的土体阻力，指出土体阻力大小对管线设计影响的双重性，即较高的水平向阻力有利于保持管线整体的稳定性，却会导致管线内弯矩的增大。刘润等[5－6]分别对埋设在砂土和软黏土中的管线受到的土体阻力进行了分析，并提出了砂土对管线阻力的经验公式和黏土中土体对管线最大阻力及其对应位移的计算公式。

在对海底管线整体屈曲的数值分析中，土体与管线相互作用的模拟至关重要。较早的管线整体屈曲模拟中，土体对管线的约束作用被简化模拟成类似于弹簧约束的线弹性模型（Pasqualino 等）[7]。随着研究的深入，管-土相互作用对管线整体屈曲形态的影响逐渐受到重视，一些更为精细的动态阻力模型被引入到整体屈曲模拟中。Villarraga 等[8]利用数值计算的方法研究了含初始缺陷埋设管线的竖直向整体屈曲变形过程，分析中分别采用了各向同性的线性、各向同性的非线性和各向异性的非线性管-土相互作用模型，分析结果显示，土体阻力模型对埋设管线的整体屈曲稳定性有着重要的影响。Cardoso 等[9]采用有限元分析软件SIGMA 研究了土坝对循环荷载作用下管线整体屈曲变形的影响，分析中采用了动态的阻力模型以模拟土坝现象对管线的约束作用，结果表明，土坝影响着管线整体屈曲后的变形形态。

为了准确地分析直铺式海底管线发生水平向整体屈曲时管线的变形及应力状态，开展相应的管-土相互作用试验，并将试验结果应用于分析中是十分必要的。本文采用砂性土体进行了室内模型试验，将所得的动态土体阻力模型进行拟合，同时基于ABAQUS 软件的二次开发，编译子程序VFRIC，模拟了在海底管线整体屈曲过程中土体对管线动态阻力。

2 动态土体阻力模型

2.1 土体对管线阻力的模型

土体阻力决定着管线的水平向整体屈曲的形态，在海底管线整体屈曲研究中占着重要的地位。作为一种粒状结构，管-土的相互作用机制远比库仑摩擦模型复杂，土体性质、管线自沉量大小、管径大小、管-土间相对位移大小等都对土体阻力有着重要的影响。

在DNV-RP-F109-2011 规范中，将土体对管线的阻力发展过程分为4 个阶段如图1 所示，图中土体对管线的阻力记为F，管线的水平向位移记为S。

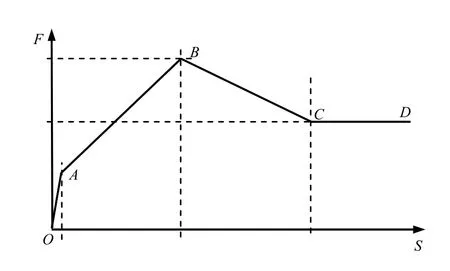
图1 土体对管线的阻力发展过程Fig.1 Soil resistance developed with pipeline’s lateral displacement

（1）第1 阶段为OA 段，此阶段土体对管线的阻力随管线的水平向位移线性增长。管线沉陷量不发生变化，此阶段的斜率被称为土体阻力系数，砂土的土体阻力系数为50～100 N/m，且随密实度的升高而增大；黏土的土阻力系数为20～40 N/m，且随黏土剪切强度上升而增大。

（2）第2 阶段为AB 段，此阶段管线的沉陷量逐渐增加，土体在管线前方形成“土拱”，土阻力F 随着前方“土拱”高度的增加而增大，最终达到阻力峰值。

（3）第3 阶段为BC 段，此阶段管线的沉陷量开始减小，土阻力由峰值开始回落。

（4）第4 阶段为CD 段，此阶段的土阻力呈现出稳定发展的趋势[11]。

2.2 室内模型试验

采用取自工程所在海域土体开展了管-土相互作用的室内试验，试验土体为级配均匀的粉砂，内摩擦角φ=30°、干密度ρ=1.742 g/cm3，试验在干砂条件下进行。模型试验系统主要由试验槽、动力系统、传力系统、数据采集系统组成，如图2 所示。

图2 管-土相互作用室内试验装置示意图Fig.2 Laboratory model test system for pipe-soil interaction

传力系统由加荷架、丝杆推杆等机械连接装置组成，对管线施加推动力；试验槽由钢化玻璃组成，并在一个侧面标上相应的刻度，用于盛放试验用土并观测土体的运动趋势；数据采集系统由拉线式位移传感器、压力传感器、动态数据采集仪、计算机和高清摄像机组成，用于记录管线的位移、所受土体阻力的大小及与不同位移相对应的管线沉陷量。试验管段外径为160 mm，长为1 m，重为4.08 kg。

由于深海管线通常不做人工挖沟掩埋的处理，管线依靠自重沉入地基土体，其埋深H 一般较浅，因此，在试验时仅研究小埋深情况下土体对管段的作用力，管径用D 表示，则试验管段的埋深条件分为不埋(H/D=0)、1/4 倍管径埋深(H/D=0.25)和半埋(H/D=0.5)共3 种情况。经多次试验，所得土体阻力如图3 所示。

图3 管线所受土体阻力-位移曲线Fig.3 Soil resistance-displacement curves of pipeline

图中横、纵坐标进行了无量纲化处理，横坐标为管段位移S 除以管径D，纵坐标为管段所受土体阻力F 除以管重W，图中同时给出了依照DNV 规范推荐公式[11]所求得的土体阻力。由图3 可以看出，试验测得的管线所受土体阻力与应用DNV 规范公式计算所得的数值一致性较好。随着管段埋设深度的增大，管段在刚开始发生水平向运动时所受的土体阻力也越大，且峰值点出现在0.6D 的水平向位移处。相同管段、不同埋深条件下，经过一段距离的水平向运动后，受到的土体阻力趋于相等，且埋深越大，趋于稳定所需要的水平向位移也越大。采用线性分段函数拟合动态土体阻力，将水平向位移为0.02 D、0.6 D 和10 D 时对应的管段受到的土体阻力F 与自重W 的比值分别记为a、b 和c，则有

式中：a、b 和c为埋置比（H/D）的函数，分别为

2.3 试验的有限元验证

采用ABAQUS 软件中的CEL(coupled Eulerian-Lagrangian technique)技术，对室内试验进行模拟验证。CEL 方法是ABAQUS 中计算流-固耦合的关键技术，它吸取了欧拉网格和拉格朗日网格的优点，采用欧氏网格中网格固定而材料可在网格中自由流动的方式建立模型，有效地解决了有关大变形、材料破坏和流体材料等诸多问题；同时建立拉式网格与欧氏网格的接触算法，利用拉式网格得到结构准确的应力-应变响应，能够有效模拟管线水平向运动时管线周围土体的破坏，因此在管-土相互作用的有限元模拟中有着广泛的应用[12－14]。

分析中忽略管段受到土体阻力而产生的微小形变，将其视为刚体，采用R3D4 单元进行模拟，土体采用EC3D8R 单元模拟，有限元模型如图4 所示。

图4 管-土相互作用有限元模型Fig.4 Pipe-soil interaction FEA model

计算时，先通过对管段施加竖向位移使得管段到达预定的埋设深度后，再对管段施加水平向位移，同时释放管段的竖向自由度，使得管段能够在竖直方向上自由移动，如图5 所示。

图5 1/4 倍埋设管段水平向运动时土体的变形云图Fig.5 Contour plot of the soil deformation with pipeline swiping laterally(for initial penetration is H/D=0.25)

经有限元计算，所得土阻力如图6 所示，可以看出，试验数据与有限元分析结果相比，有限元模拟结果在达到峰值后迅速下降，较试验结果更快趋于稳定。这是由于有限元模拟时，管段的竖直向为自由状态，没有约束，因此，管段向上移动的速度快，能很快达到残余土体阻力对应的管段埋深。有限元计算结果与试验测定的最终残余土体阻力值基本相当。

图6 有限元与试验结果的对比Fig.6 Comparison between the test and FEA results

考虑到本文的研究对象为铺设于海底的管线，采用CEL 方法计算管线在水下饱和砂土中水平向运动时受到的土体阻力，研究管线分别在饱和砂土与干砂中运动时受到的水平向土体阻力的差异，有代表性的结果见图7。

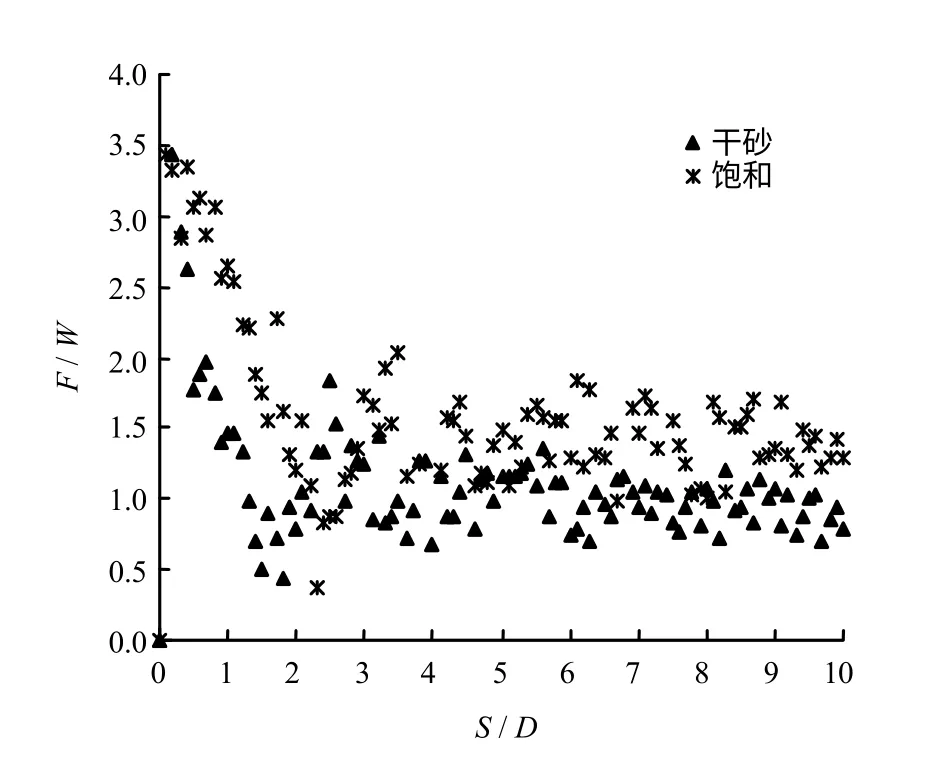
图7 不同含水率砂土对管线(H/D=0.25)的阻力Fig.7 Resistance of sand to pipeline with different water ratios(H/D=0.25)

由图7 可以看出，不同含水率的砂土对土体阻力的影响较小。两种含水率砂土的峰值阻力F 大小一致，干砂为3.44W，饱和砂土为3.45W。不同含水率砂土中，残余土体阻力系数的大小及其对应的位移稍有不同，干砂中残余土体阻力F 较小且所需的位移S 较短，分别为0.65W 和2.2D，而饱和砂土中对应的为1.23W 和2.7D。

在ABAQUS 中，物体间切向的摩擦行为内置的模拟方法是采用的“罚”函数进行模拟，即通过规定一个固定的摩擦系数模拟物体间的库仑摩擦作用。这种接触本构关系下，物体间的切向阻力的大小仅与物体间竖向作用力和摩擦系数的大小有关，阻力不会随物体间相对位移大小的改变而改变，无法模拟出与位移大小相关动态阻力。

为了将动态的土体约束模型引入有限元分析中，采用ABAQUS 用户子程序VFRIC 进行二次开发以模拟土体对管线的约束。子程序VFRIC 用于在动力显示分析中，定义接触的两个表面间复杂的摩擦行为，能将阻力系数表达为多种状态变量的函数[15]。在子程序VFRIC 中，每一增量步计算后解算器输出变量中，仅有该增量步所得的相对位移大小，因此，在编译子程序时，预先定义一个表示总位移量S 的状态变量statev(i_usv_dis,ncontact)，并在每次开始调用子程序时，将该增量步所得的位移增量累积到状态变量statev(i_usv_dis,ncontact)中，然后根据变量statev(i_usv_dis,ncontact)的大小，选择不同的函数关系式计算阻力系数k，详细的子程序编译部分如下：

3 动态土阻力模型的应用

3.1 水平向整体屈曲的分析模型

采用有限元分析ABAQUS 对海底管道的整体屈曲进行了分析。管线参数及土体性质采用渤海某工程的数据，具体参数见表1、2。采用Explicit 算法，管线长度为2 km，采用PIPE31 单元模拟，用模态分析法[16]在管线中点引入初始缺陷。管线的初始缺陷是由于管线在制造和铺设过程中造成的初始挠曲，初始缺陷的存在对管线的临界屈曲荷载、整体屈曲变形形态有着重要的影响。管线初始缺陷的主要参数为初始缺陷幅值V0和初始缺陷波长L0，计算中引入幅值为0.5 m、波长为70 m 的初始缺陷，分析中对管线施加80 ℃的设计温差，并约束管线两端的水平向变形。土体采用C3D8R 单元，土体侧面约束水平向位移，底面固定约束，所建模型如图8 所示。

表1 管线参数Table 1 Parameters of pipeline

表2 地基土体参数Table 2 Parameters of seabed soil

分析中分别用“罚”函数法和子程序VFRIC 法模拟管-土间的相互作用，并将采用“罚”函数的模型称为P 模型，将采用子程序的模型称为V 模型。根据DNV-RP-F109，管线在自重作用下的初始自沉量H/D=0.037[11]，代入式（1），求得管线所受的土体阻力模型作为V 模型的控制函数。P 模型中土体阻力系数为0.63，该值的大小等于管线最终受到的土体阻力系数值。

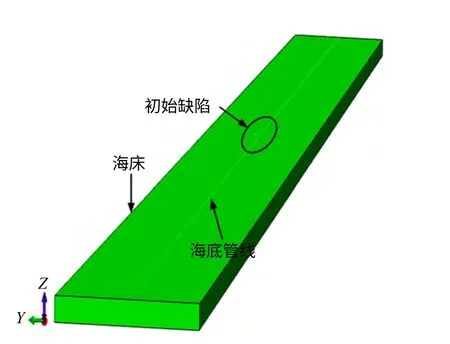
图8 有限元分析模型Fig.8 FEA model

3.2 水平向整体屈曲分析结果

3.2.1 土体对管线的阻力

子程序对阻力系数的定义采用的是基本增量法，即根据每一级增量步开始时的管线水平向总位移大小来确定阻力系数k，并在增量步中保持不变，而管线的整体屈曲过程中存在着位移的突变式增长，当前、后两个相邻增量步间位移差较大时，这种算法所计算得出的阻力系数k 与子程序中函数关系所表达的动态土体阻力间可能存在着一定的误差。由于管线中点处位移突变式增长现象严重，因此，将该点处所受阻力与试验所得的动态阻力模型进行比较，可以反映实际计算中受到的阻力与理想模型间差距最大的情况，有利于评价子程序的可靠性。计算后提取V 模型中管线中点处实际受到的土体阻力系数，并与试验所得的动态阻力模型进行比较，结果如图9 所示。

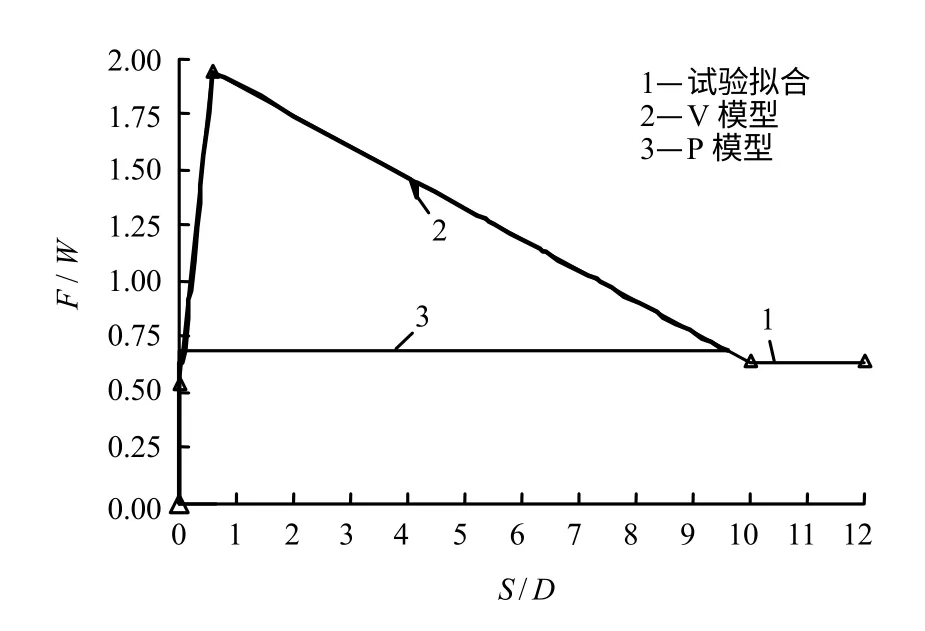
图9 土阻力计算结果对比Fig.9 Comparison of calculation results of soil resistance

由图9 可知，V 模型中管线实际受到的阻力与试验所得的阻力模型基本一致，由此证明子程序成功地将试验所得的阻力模型引入管线整体屈曲分析中，实现了土体阻力随管-土间相对位移大小的变化而变化。

3.2.2 管线的临界屈曲力

管线受到温度荷载的作用后，由于土体的约束作用管线不能自由变形，截面会累积压缩应力。随着升温的继续，温度应力超过土体阻力而导致整体屈曲的发生。在该过程中，管线轴力呈现先上升后随着变形的增大而下降的趋势。提取P 模型和V 模型管线中点处的轴力和水平向位移，建立管线中点轴力-位移的关系曲线，如图10 所示。

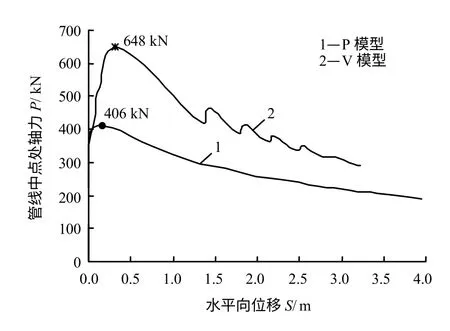
图10 管线中点处轴力随位移的变化曲线Fig.10 Axial force-lateral displacement curves of pipeline midpoint

由图10 可知，P 模型和V 模型的轴力先随着水平向位移的增加而增大，达到峰值时，管线发生了水平向的整体屈曲，管线截面累积的轴力随变形的增加而释放。P 模型和V 模型的临界屈曲轴力较大，分别为648、406 kN，而后随着变形的继续发展，两个模型中截面轴力的差距逐渐减小。可见土体阻力的变化导致了管线临界屈曲轴力的改变。本文建立的子程序可有效地模拟土体对管线阻力随管线变形的变化，即在管线位移较小时土体的约束较强，随后逐渐减弱趋于稳定，能有利于准确求得海底管线在一定条件下发生整体屈曲时的临界屈曲力，克服以残余土体阻力值作为土体阻力大小的P模型对临界轴力的过低估计。

3.2.3 管线的水平向变形

为体现管线受到温度荷载作用后产生水平向变形的过程，提取不同温度时管线上各点的位移，P模型和V 模型变形形态的发展过程分别如图11(a)、11(b)所示。

由图可知，当采用V 模型模拟土阻力时，由于土阻力存在峰值，使得计算得到的管线变形幅值比P 模型小。例如，当温差为20 ℃时，V 模型计算得到的最大水平向位移为0.15 m，而P 模型为0.35 m。两个模型计算得到的管线最终变形量也有所不同，V 模型在温差为80 ℃时水平向变形幅值为3.35 m，变形段长度为240 m，P 模型对应的数值分别为4.01 m 和310 m。可见考虑土体阻力的变化过程，对判断管线的最终变形也会有所影响。

将图11 中两个模型管线的最大正向变形点和最大负向变形点称为A、B。A、B 两点的水平向位移随温差的变化曲线如图12(a)、12(b)所示。

图11 不同温差下管线的变形Fig.11 Pipeline deformations at different temperature differences

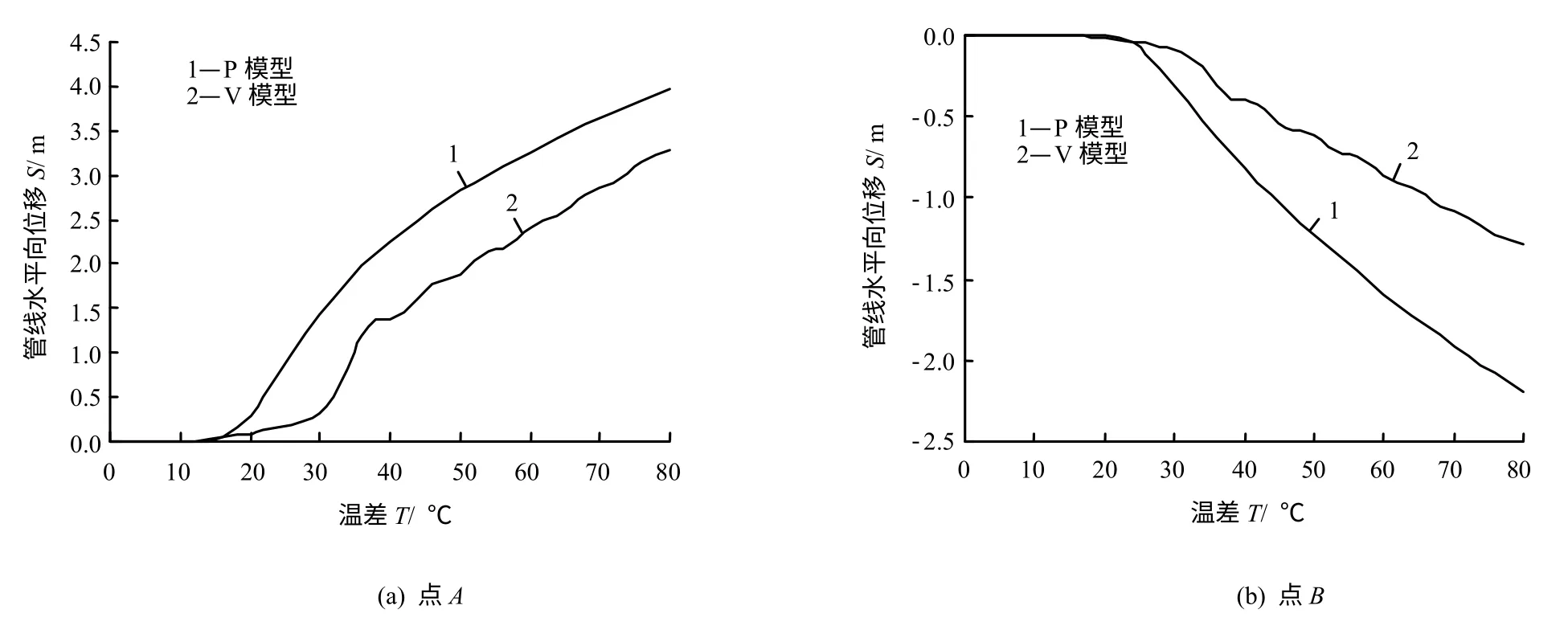
图12 两种模型管线水平向位移随温差的变化曲线Fig.12 Curves of lateral displacement with temperature difference of pipelines in two models

由图12(a)可知，P 模型中点A 在16 ℃时开始出现较大的位移增长且整个增长过程较为均匀，而V 模型中点A 较大的位移增长出现在30 ℃，且在30 ℃前仅有小幅度变化，说明了V 模型中管线在发生较小位移时受到较强的土体阻力，管线的变形被限制，当温度升至30 ℃左右时，管线最大水平向位移为0.324 m，约为1 倍管径大小，对应土体阻力曲线（见图9）可知，此时管线受到的土体阻力已经进入下降阶段，即管线中点A 附近管段受到的土阻力下降，因此，管线中点处位移产生了突变式增长。在图12(b)中可以观察到相同的现象，P 模型点B 的水平位移在温差为20 ℃时开始匀速增加，而V模型中点B 的水平位移在温差为32 ℃时产生了突变而后位移的增长较为均匀。P 模型两点A、B 的最终位移分别为3.96 m 和2.19 m，点B 最终位移为点A 最终位移的55 %，而V 模型两点A、B 的最终位移分别为3.29 m 和1.29 m，点B 最终位移为点A最终位移的39 %，说明动态土体模型中变形更趋于向中点处集中，负向位移受到抑制。

3.2.4 管线的最大弯矩和应变

管线受热发生整体屈曲后，伴随着水平向变形的发展，管线截面内将产生并累积一定的弯矩和应变。P 模型和V 模型管线中最大弯矩和应变随温差的变化曲线分别如图13、14 所示。

图13 两种模型管线中最大弯矩随温差的变化曲线Fig.13 Curves of maximum bending moment with temperature difference of pipelines in two models

图14 管线中最大拉、压应变随温差的变化曲线Fig.14 Curves of maximum compressive,tensile strain with temperature difference of pipelines in two models

由图13、14 可知，管线截面内弯矩和应变的增长与水平向位移的变化保持着较好的一致性。P 模型中管线所受弯矩和拉、压应变均呈匀速增长，而V模型中则存在突变现象，且突变温度与图12 中 管线的位移突变温度一致。从图13 中可以看出，V 模型中管线截面的最大弯矩在温差为30 ℃前较小，30 ℃后管线发生整体屈曲，管壁内弯矩迅速增大。V模型和P 模型的最终弯矩值分别为599、479 kN⋅m 。从图14 中也可以观察到类似的变化，V 模型中管线的压缩和拉伸应变分别在温差为28 ℃和32 ℃时出现突变并迅速增长。V 模型和P 模型的最终压应变分别为0.22 %和0.16 %，最终拉应变分别为0.25 %和0.23 %。

根据DNV 规范对整体屈曲后管线失效的判断标准[17]，变形产生的弯矩和应变对管线的安全十分不利。由图12、13 可知，V 模型中屈曲后管线的最大弯矩和应变大于P 模型的计算值，即不考虑土体阻力随管线位移的变化过程，会低估整体屈曲后管线的应力、应变值，产生偏于危险的管线设计。

4 结 论

（1）通过室内模型试验，获得了不同浅埋条件下管线受到的水平向土体阻力与管线位移间的关系，通过对试验数据的拟合，建立了峰值阻力、残余土阻力与管线埋深间的函数关系。

（2）通过预设状态变量，对每个增量步中管线的水平向增量位移进行累加和传递，解决了子程序VFRIC 中无法直接输出总位移量的问题，从而实现了管线整体屈曲分析中对土体动态阻力特性的模拟。

（3）不同土体阻力模型对管线整体屈曲分析结果有较大影响，当采用动态阻力模型时，管线整体屈曲临界轴力明显提高，变形更为集中，但幅值较小，对管线安全不利的状态量（弯矩和应变）数值较大，因此，忽略土体阻力随管线位移的变化历程，会低估整体屈曲后管线的应力、应变，造成管线设计偏于危险。

[1]LYONS C G.Soil resistance to lateral sliding of marine pipelines[C]//Offshore Technology Conference.Houston:[s.n.],1973.

[2]BRENNODDEN H,SVEGGEN O,WAGNER D A,et al.Full-scale pipe-soil interaction tests[C]//Offshore Technology Conference.Houston:[s.n.],1986.

[3]BRUTON D,WHITE D,CHEUK C,et al.Pipe/soil interaction behavior during lateral buckling including large-amplitude cyclic displacement tests by the safebuck JIP[C]//Offshore Technology Conference.Houston:[s.n.],2006.

[4]BRUTON D A S,WHITE D J,CARR M,et al.Pipe-soil interaction during lateral buckling and pipeline walking——the safe buck JIP[C]//Offshore Technology Conference.Houston:[s.n.],2008.

[5]刘润,闫澍旺,王洪播,等.砂土对埋设管线约束作用的模型试验研究[J].岩土工程学报,2011,33(4):559－565.LIU Run,YAN Shu-wang,WANG Hong-bo,et al.Model tests on soil restraint to pipelines buried in sand[J].Chinese Journal of Geotechnical Engineering,2011,33(4):559－565.

[6]LIU R,YAN S,WU X.Model test studies on soil restraint to pipeline buried in Bohai soft clay[J].Journal of Pipeline Systems Engineering and Practice,2012,4(1):49－56.

[7]PASQUALINO I P,ALVES J L D,BATTISTA R C.Failure simulation of a buried pipeline under thermal loading[C]//Proceedings of the 20th International Conference on Offshore Mechanics and Arctic Engineering(OMAE).Brazil:American Society of Mechanical Engineers,2001.

[8]VILLARRAGA J A,RODRĺGUEZ J F,MARTĺNEZ C.Buried pipe modeling with initial imperfections[J].Journal of Pressure Vessel Technology,2004,126(2):250－257.

[9]DE OLIVEIRA CARDOSO C,DA COSTA A M,et al.HP-HT pipeline cyclic behavior considering soil berms effect[C]//Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering(OMAE).Hamburg:[s.n.],2006.

[10]American Lifelines Alliance,Guideline for the Design of Buried Steel Pipe[S].[S.l.]:American Society of Civil Engineers(ASCE),2005.

[11]DET NORSKE VERITAS.DNV-RP-F109,on-bottom stability design of submarine pipelines[S].Oslo:[s.n.],2011.

[12]JUKES P,ELTAHER A,SUN J.The latest developments in the design and simulation of deepwater subsea oil and gas pipelines using FEA[C]//Third ISOPE International Deep-Ocean Technology Symposium.Beijing:International Society of Offshore and Polar Engineers,2009.

[13]PIKE K,DUAN G,SUN J,et al.Comprehensive FEA of thermal mitigation buoyancy module(TMBM)——Soil interaction using the coupled Eulerian-Lagrangian(CEL)Method[C]//ASME 2010 29th International Conference on Ocean,Offshore and Arctic Engineering.Shanghai:American Society of Mechanical Engineers,2010.

[14]DATYE D V.On the Calibration of coefficients of friction for pipeline-seabed interaction[C]//ASME 2010 29th International Conference on Ocean,Offshore and Arctic Engineering.Shanghai:American Society of Mechanical Engineers,2010.

[15]HIBBITTE K.ABAQUS User Subroutines Reference Manual[M].[S.l.]:HKS Company,2011.

[16]LIU R,XIONG H,WU X,et al.Numerical studies on global buckling of subsea pipelines[J].Ocean Engineering,2014,78(1):62－72.

[17]DET NORSKE VERITAS.DNV-OS-F101,Submarine pipeline systems[S].Oslo:[s.n.],2012.