基于岩石损伤本构的破碎比功评价模型研究与应用

蔡 灿 ，伍开松 ，袁晓红，吴霁薇，赵 攀

（1.西南石油大学 机电工程学院，四川 成都 610500；2.西南石油大学 钻头研究所，四川 成都 610500；3.壳牌中国勘探开发有限公司，四川 成都 610500）

1 引 言

钻头破岩效果不仅与钻压、转速及地质条件等相关，在很大程度上是由钻头上的牙齿决定的。因此，牙齿的破岩效果评价准则与方法是否能科学地反映实际工况，不仅是国内外矿业学者和石油钻井工程师关注的重点，而且也是新型牙齿的设计与优化的基础。

自20 世纪80年代有学者提出煤矿的破碎功研究后[1−2]，破碎比功的研究工作不仅继续深入，还被应用于地下工程灾害防治[3]。杨迎新等[4]将破碎比功成功应用于牙齿破岩效率评价，并对牙齿齿形进行了评价和优选应用。该方法经过多年应用，已被作为牙齿齿形评价的准则，或者经过改进和修正后得到更广泛的研究和应用[5−7]。目前的破碎功学说已经考虑到损伤、裂纹等对破碎的影响[8]，但破碎比功的研究与应用都忽略了未破碎的损伤区。从能量上看，这部分未破碎区实际上也吸收了牙齿的大量输入功，并转化为裂纹、孔洞和其他声热能；从矿业和石油工程中牙齿的连续破碎来看，这些临近破碎区的损伤区将大大减小下一次破碎的输入功，这使得第1 次计算的破碎比功不能完整地评价牙齿连续破碎的效果。基于以上分析可知，研究一种考虑损伤区的破碎比功评价模型对客观评价牙齿连续破碎的真实效果是有必要的。

基于上述分析，对损伤区域的破碎功采用了加权计入，统一了能量输入的破碎区和未破碎区，建立了考虑损伤区的破碎比功评价模型。采用ANSYS二次开发损伤本构模型，对单齿压入破碎比功进行了数值仿真试验。然后与试验测试中的一次破碎和二次破碎体积的对比验证，检验该模型的正确性。

2 考虑损伤的破碎比功评价模型

破碎比功是用来衡量牙齿的破岩效果的，是破碎单位体积岩石所消耗的能量，它是岩石抗破碎能力大小的标准[9]。一般认为，牙轮钻头正常钻速下，牙齿破岩可近似认为是静态压入[8]，因此，可根据牙齿静压入试验来评价齿形。具体作法是用静压入试验得到的牙齿垂直压入时外载荷F 与牙齿侵入深度h 的函数关系 f(h)，计算出外力F 在牙齿压入直至岩石破碎全过程做的功为W，测出破碎坑的体积V，然后计算破碎比功AV，即单位岩石破碎体积的破碎功，公式如下：

用AV作为牙齿破岩效率的定量评价依据，认为 AV越大，破碎效率越低；AV越小，破碎效率越高[10－11]。

但上述破碎比功主要是针对一次凿岩破碎效果的，而石油工程钻井过程中岩石是被牙齿连续破碎的，这与仅用一次凿岩效果去评价牙齿整个周期的凿岩效率是有区别的。要想得到牙齿在连续凿击下的整体凿岩效果，就应当考虑初次凿击产生的破碎区与未破碎损伤区的综合影响。

针对实际问题的需要，应当研究一种新的破碎比功模型，这种模型应当具备两个重要特征：①在破碎比功中应当计入未破碎但受到损伤的区域，该区域对牙齿第2 次凿击效果有重要影响；② 该模型不仅含有第1 次破碎的效果评价，还应当能够对下一次破碎的效果进行准确评价和预测。

2.1 基于损伤的破碎比功模型

岩石受到连续凿击可以看成前后两次凿击的多次重复，因此，可以以两次凿击作为基本的研究单元来建立新的破碎比功评价模型。由于牙齿破岩的高度非线性和一定的随机性，因此，本文所提的破碎比功模型实际上包含试验和数值仿真两个模型，这既能保证准确性和适用性，又能降低试验成本和次数。

2.1.1 试验测试的破碎比功模型

式（1）是破岩破碎比功的原始表达式，根据上述分析，引入第2 次破碎之后，试验第1 次破碎比功可表达如下：

式中：W1为牙齿第1 次压入的输入功；V1为第1 次的破碎体积。

由于试验测试时载荷施加在同一牙齿上的，牙齿上受力面积S 是一样的。由于力 F1与压力 P1是线性关系（F1=P1S），为了简化计算，上式可整理为

式中：H1为第1 次压入深度。由于牙齿在第1 次破碎坑的基础上作第2 次破碎，因此，第2 次破岩破碎比功（以下简称第2 次破碎比功）为牙齿在经历单次准静态压入后，在同一损伤（或破碎）部位的再次压入，其第2 次压入的输出功与该次造成的破碎体积之比。其表达式如下：

式中：P2、H2、V2分别为第2 次压入的压力、深度、体积。

两次凿击是连续破岩的基本单元，因此，前后两次破碎的总破碎比功（以下简称试验前两次总破碎比功）是牙齿综合破岩效果的评价指标，是牙齿前后两次压入的总输出功与其总破碎体积之间的比值，表达式为

2.1.2 基于损伤本构的仿真破碎比功评价模型

试验无法判断损伤区的破碎效果，也不能预测第1 次压入后的后续破碎效果。当建立了岩石的损伤本构模型并将该模型编程嵌入ANSYS 求解器后，可以通过数值仿真来近似模拟多次压入的试验。在此新的仿真试验条件下，结合连续介质损伤力学，提出了描述岩石连续破碎效果的评价指标——仿真总有效理论破碎比功，其表达为

式中：Pm为m 次压入的压力（MPa）；Hm为m 次压入的压入深度（mm）；VElem为图1 中损伤单元的单元体积；D*为该损伤单元的损伤值；i为损伤单元的序号（Element Number），范围从min～max，可由ANSYS 内部提取函数获得。

图1 仿真一次破碎产生的潜在破碎区单元损伤云图Fig.1 Potential damage contour of crushing area subject to the first impression by numerical simulation

式（6）对所有损伤岩石单元进行体积求和，并采用损伤权重计入潜在破碎体积中。与试验破碎比功不同，该式输入功不仅计入分母中的已破碎区，还包括了未破碎损伤区，这使得岩石的消耗功或能量更加接近外部输入功。

基于上述理论分析，进一步提出仿真牙齿压入第1 次有效破碎比功（以下简称一次有效破碎比功）：

图2 仿真第1 次破碎的破碎区单元损伤云图Fig.2 Damage contour of crushing area subject to the first impression by numerical simulation

同理，可定义仿真牙齿第2 次压入的有效破碎比功（以下简称第2 次有效破碎比功），可同样用式（7）表示。

图3 仿真第2 次破碎的破碎区单元损伤云图Fig.3 Damage contour of crushing area subject to the second impression by numerical simulation

考虑岩石损伤软化是由于微裂隙发展所导致的，许多学者都指出，岩石损伤变量是应变的指数函数，并且损伤参量的变化应当与岩石初始状态和损伤阀值有关。可以定义损伤变量D 时，关于孔隙率变化的指数函数关系为

式中：φm为孔隙度变化的阀值。

将式（8）代入式（9）后则有

经典连续介质损伤理论认为

式中：σ为介质主应力；E为弹性模量；Dε为单元损伤量。

因此，式（11）可化简为

以岩石受到的连续两次凿击作为基本研究单元来建立新的破碎比功评价模型在试验和仿真中得到统一，结合起来即可对牙齿连续破岩效果进行有效的预测和评价。

3 自定义损伤本构模型及二次开发

3.1 自定义损伤本构模型

上述模型的基础在于自定义损伤本构模型并将其二次开发嵌入ANSYS 软件中。蔡灿等[12]基于岩石内部孔隙、裂隙与裂纹等变化建立了孔隙度变量演化函数。在加载过程中，岩石内部孔隙、裂隙与微裂纹有些在变大，有些发生扩展与贯通，还有些存在闭合（即岩石力学试验中的压实现象）。尤其在压缩阶段的弹性变形初期，孔隙、裂隙与微裂纹的闭合影响十分显著[13−14]。因此，引入孔隙度变化率系数K 和孔隙闭合参数δ 。

任意应变时刻的孔隙度为

式中：ε1、ε2和 ε3分别为岩石微元三向主应力；φ(ε)

考虑到岩石内部压缩和拉伸的不同破坏形式，将上述孔隙度、损伤分别定义，即拉伸孔隙度φt和拉伸损伤Dt；压缩孔隙度φc与压缩损伤Dc，并采用下式进行加权计算，加权因子计算式为

式中：tt为拉伸损伤的加权因子；cc为压缩损伤加权因子。由于本文重点是岩石破碎比功评价模型，限于篇幅，此处对自定义损伤本构不再赘述。

3.2 ANSYS 二次开发流程

ANSYS 公司为用户提供的本构模型二次开发接口可以解决自定义的材料本构模型。限于篇幅，仅介绍二次开发本构材料程序流程（见图4）。利用岩石自定义损伤本构模型程序进行编译链接，生成可执行的ANSYS.EXE 求解器。使用上述求解器就可以使用自编损伤本构模型进行分析。

3.3 基于损伤的破碎比功模型数值试验方法

（1）有限元建模

根据江钻公司提供的球形牙齿尺寸[14]，建立了球形齿的模型（如图5 所示）。该牙齿半径为7.18 mm，齿顶柱台的倾角为20°，齿顶球半径为4.72 mm，牙齿总高为21.44 mm。

图4 损伤本构二次开发的程序流程图Fig.4 Flow chart of the secondly developed damage constitutive model

图5 牙齿与岩石接触模型的有限元建模Fig.5 Modeling of tooth-rock contact by finit element

岩石为砂岩，材料参数如表1 所示，输入方式如图6 所示。模型为90°圆柱体，直径为180 mm，高度为50 mm。该岩石模型与牙齿模型相比足够大，可以忽略边界的影响。所有模型均为1/4 模型，以达到较好的精度和合理的计算机时。为了提高接触区域的计算精度，对接触区域进行网格的细化分。

图6 岩石自定义损伤本构材料参数输入Fig.6 Parameter import using the user-defined damage constitutive model

表1 岩石自定义本构的力学参数Table 1 Mechanics parameters of user-defined constitutive model

4 新破碎比功模型的应用研究

4.1 试验验证

西南石油大学钻头研究所杨迎新[15]和古剑飞[16]等设计了牙齿静压入试验（如图7 所示），试验时将牙齿安装在压力传感器的端头，岩石表面垂直于牙齿轴线，用液压缓慢加载。在此过程中，连续测量牙齿的载荷F 和侵入岩石的深度H 并且记录，绘出它们的关系曲线，同时观察压入区域周围岩石的变化，直至发生岩石的脆性破碎或体积破碎。中间中断一次测试破碎体积V1，结束后再测试一次破碎体积(V1+V2)，详细过程请参考文献 [17]。

在牙齿压入岩石过程中测试：①第1 次体积破碎的门限值，测试载荷F 与位移h 的关系曲线和极限值。②对破碎坑进行三维扫描或拍摄照片，测试岩石破碎的基本数据。

图7 单齿静压入试验原理Fig.7 The work principle of a single-tooth impression

4.2 自定义损伤本构程序的单齿压入验证

为了验证该损伤本构可以应用于破碎比功模型，有必要选用单齿单次压入破碎进行验证。该验证过程既可以验证模型正确性，又可分析单齿破碎机制。分析压缩孔隙度分布（如图8 所示）可知，在牙齿作用正下方的岩石孔隙度已经达到了3.672，表明岩石已经完全破碎，这与图9 Hagan[18]在钠玻璃的侵入试验结果一致。下方出现了孔隙度扩展的两个侧方向，角度约为45°，与单齿静压岩石的试验现象十分吻合。

图8 压缩孔隙度云图Fig.8 Contour of the compressed porosity

图9 钠玻璃受压内部裂纹扩展图Fig.9 Image of the crack development of a sodium glass

图10 复合损伤参数分布云图Fig.10 Contour of the combined damage parameter

分析复合损伤的分布（如图10 所示）可知，岩石在接触点下方的损伤值达到了1，已经发生了破碎。但在破碎区的正下方，岩石孔隙度接近或者达到−1，说明此处岩石基本上被压实，并且在压实区有向两侧流动的趋势，形成了剪切角度，这与破碎坑的结构（如图11 所示）十分吻合。

图11 压入后的岩石破坏现象Fig.11 Rock crushing situation under impress

为了进一步验证损伤本构模型的的正确性，对该岩石内部损伤与应力进行定量对比验证，采用钻头研究所前人试验数据进行对比（如表2 所示）。

取该岩石表面沿径向分布的节点，得到径向的岩石孔隙度和损伤变化（如图12、13 所示），它表明，在牙齿压入内侧岩石孔隙度已经超过1，达到了完全损伤。在约2 mm 处，岩石损伤呈压实损伤，并且损伤沿径向快速下降趋近于0。

图12 径向孔隙度变化Fig.12 Porosity change in the radial direction

通过上述单齿压入破岩机制的分析，与试验及以往理论经验的对比，从定量和定性角度均说明本文的损伤本构是正确的，可以应用于损伤的破碎比功研究中。

图13 径向复合损伤Fig.13 Composite damage in the radial direction

4.3 在单齿破岩效率分析和齿形评价中的应用

将上述损伤本构模型结合本文提出的破碎比功模型，可应用于牙齿齿形优选或者牙齿破岩效果评价中去。通过一次破碎的试验校准，就可以推算出牙齿后续二次破碎的效果，并且综合评价牙齿连续破岩的效果。这不仅可大大减小试验次数，节约试验成本，也可以避免试验中人为因素产生的误差。

首先分析牙齿的试验和仿真一次破碎比功规律（如图14 所示）可以发现，随着载荷的增大，破碎比功整体有下降趋势。这种趋势有两个特点：①个别试验数据有一定的随机性，可能大于也可能小于理论值；② 下降趋势比较缓慢。由于仿真能够排除破碎体积测试误差，其与破碎比功变化趋势相比试验更加规律。

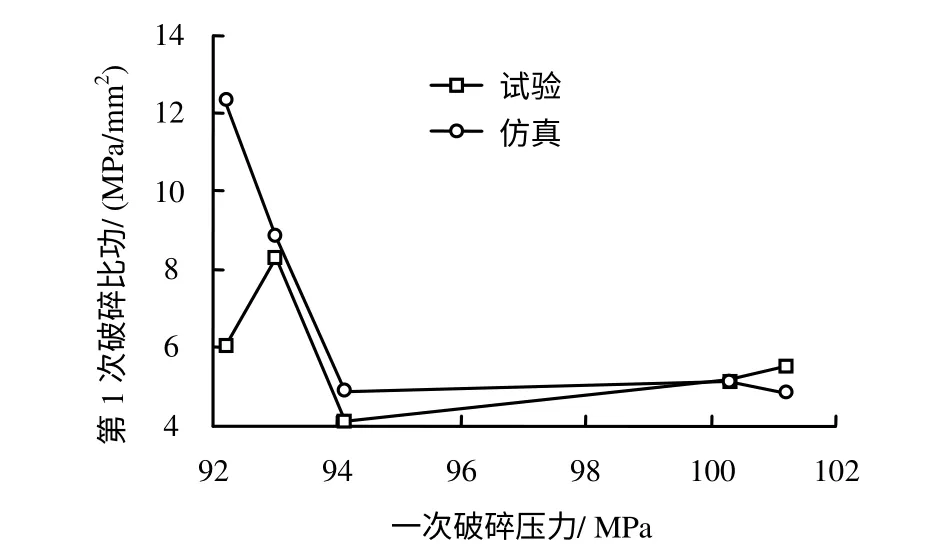
图14 试验与仿真的第1 次破碎比功对比Fig.14 Comparison of experimental and numerical results of the first crushing work ratio

对比第2 次试验破碎比功和仿真第2 次破碎比功（如图15 所示），其整体随载荷的增大也有缓慢下降趋势。与第1 次破碎比功相比，第2 次破碎比功平均值仅为第1 次破碎比功平均值的1/5（18.62%）。这说明，在同一点的再次破碎会大大提高岩石的破碎效率，提高牙齿输入功的转化。这也间接说明，引入第2 次破碎比功去评价牙齿破岩效果对岩石破碎和牙齿优选十分重要。

图15 试验与仿真的第2 次破碎比功对比Fig.15 Comparison of experimental and numerical results of the second crushing work ratio

为了验证本文提出的仿真预测总破碎比功的有效性，有必要将前两次压入总的破碎比功与之对比。由于做第3、4 次乃至后续的压入破碎试验误差太大，所以本文只选取前两次。通过前两次总的破碎比功曲线，能够发现破碎比功的整体变化趋势。如果压入的仿真预测总破碎比功趋势与试验前两次破碎比功一致，说明基于损伤本构的仿真预测总破碎比功是有效的。

通过对比两者的曲线可以发现（见图16），随着压入载荷的增大，破碎比功的趋势基本呈现一致变化，误差分布有一定随机性。图17为仿真预测总破碎比功与试验测试的前两次破碎比功对比，由于仿真预测总破碎比功的分母是所有损伤单元体积的加权求和，故该指标的值比仅前两次的破碎比功要小很多，约为后者的10%。此外随着载荷的增大，两者之间的误差也越来越大，仿真模拟的破碎体积比实际破碎体积要偏小。

图16 前两次总破碎比功对比Fig.16 Comparison of experimental and numerical results of the first and the second total crushing work ratios

图17 试验前两次总破碎比功与仿真预测总破碎比功对比Fig.17 Comparison of total crushing work ratio of the first two experimental results and numerical predictions

由于试验中载荷从92～102 MPa 不等，破碎比功值差距并不大，因此，对比第1 次破碎比功、第2 次破碎比功和总的破碎比功对分析多次加载破碎岩石效果有一定意义。表3为各项破碎比功的平均值，根据该表结果可以发现，不论是试验或是仿真，第2 次破碎比功均比第1 次破碎比功下降70%～90%不等。由于第2 次破碎比功的大幅度下降，两次总的破碎比功也大大降低。这说明在钻头破岩中，连续在同一破碎点或者已经损伤的岩石部位再进行加载，会大大提高破碎岩石的效率。通过对比该表也可以发现，虽然仿真与试验之间存在一定误差，但整体平均值的误差都在20%以下，这对非均质的岩石材料来说精度已经算比较高了。

表3 各破碎比功平均值的对比Table 3 Comparison of the average crushing work ratios

因此，通过建立损伤本构模型，并结合ANSYS二次开发，建立基于损伤的牙齿破碎新评价模型是适用于牙齿齿形评价和岩石破碎效果评价的，可以代替较为繁琐和不确定性的试验来综合判断牙齿的破碎比功。

5 结 论

（1）基于自定义损伤本构的岩石破碎比功可以用于评价牙齿的二次及连续破碎效果的预测及评价，其中仿真总预测破碎比功还可以作为连续破碎效果的评价指标。

（2）随着牙齿的压入载荷增加，破碎比功会缓慢下降。它表明，当载荷增大到一定后，继续增大载荷并不会显著提高破碎效果。

（3）第2 次破碎比功约为第1 次破碎比功的20%，说明一次破碎后的岩石损伤对岩石破碎影响十分显著，在同一处的连续破碎将会大大减小牙齿的破碎效率，提高牙齿输入功的转化效率。

[1]蔡成功,熊亚选.突出危险煤破碎功理论与试验研究[J].煤炭学报,2005,30(1):63－69.CAI Cheng-gong,XIONG Ya-xuan.Theoretical and experimental study on crushing energy of outburst proneness coal[J].Journal of China Coal Society,2005,30(1):63－69.

[2]赵伏军,李夕兵.动静载荷耦合作用下岩石破碎理论分析及试验研究[J].岩石力学与工程学报,2005,24(8):1315－1320.ZHAO Fu-jun,LI Xi-bing.Theoretical analysis and experiments of rock fragmentation under coupling dynamic and static loads[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(8):1315－1320.

[3]李国华,陶兴华.动、静载岩石破碎比功试验研究[J].岩石力学与工程学报,2004,23(14):2448－2454.LI Guo-hua,TAO Xing-hua.Testing study on crushing work ratio of rock under dynamic and static load[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(14):1448－1454.

[4]杨迎新,张文卫,李斌,等.牙齿破岩效率的评价及牙齿优选探讨[J].岩石力学与工程学报,2001,20(1):110－113.YANG Ying-xin,ZHANG Wen-wei,LI Bin,et al.Effect evaluation on insert penetration to rock and optimization of insert shape[J].Chinese Journal of Rock Mechanics and Engineering,2001,20(1):110－113.

[5]郭臣业,鲜学福,吴轩洪,等.岩石破碎功、坚固性系数、强度关系的试验研究[J].重庆建筑大学学报,2008,30(6):28－31.GUO Chen-ye,XIAN Xue-fu,WU Xuan-hong,et al.The relationship among rock crushing energy,the Protodyakonov coefficient and rock strength[J].Journal of Chongqing Jianzhu University,2008,30(6):28－31.

[6]李国华,陶兴华.动静载岩石破碎比功试验研究[J].岩石力学与工程学报,2004,23(14):2448－2454.LI Guo-hua,TAO Xing-hua.Testing study on crushing work ratio of rock under dynamic and static load[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(14):2448－2454.

[7]闫铁,李玮,毕雪亮,等.一种基于破碎比功的岩石破碎效率评价新方法[J].石油学报,2009,30(2):291－294.YAN Tie,LI Wei,BI Xue-liang,et al.A new evaluation method for rock-crushing efficiency based on crushing work ratio[J].Acta Petrolei Sinica,2009,30(2):291－294.

[8]马德坤.牙轮钻头工作力学(第1版)[M].北京:石油工业出版社,1984.

[9]李世忠,杨学涵,何玉明,等.钻探工艺学(上册)[M].北京:北京地质出版社,1980.

[10]张祖培,刘宝昌.碎岩工程学[M].北京:地质出版社,2004,32－42.

[11]徐小荷,余静.岩石破碎学[M].北京:煤炭工业出版社,1984.

[12]蔡灿,伍开松,袁晓红,等.中低应变率下的岩石损伤本构模型研究[J].岩土力学,2015,36(3):795－802.CAI Can,WU Kai-song,YUAN Xiao-hong.Study of damage dynamic constitutive model of rock under medium and low strain rate[J].Rock and Soil Mechanics,2015,36(3):795－802.

[13]孙强,薛晓辉,朱术云.岩石脆性破坏临界信息综合识别[J].固体力学学报,2013,34(3):311－318.SUN Qiang,XUE Xiao-hui,ZHU Shu-yun.The identification method of critical information for rock brittle failure[J].Chinese Journal of Solid Mechanics,2013,34(3):311－318.

[14]葛修润,任建喜,蒲毅彬,等.岩石疲劳损伤扩展规律CT细观分析初探[J].岩土工程学报,2001,23(2):191－195.GE Xiu-run,REN Jian-xi,PU Yi-bi,et al.Primary study of CT real-time testing of fatiguemeso-damage propagation law of rock[J].Chinese Journal of Geotechnical Engineering,2001,23(2):191－195.

[15]杨迎新,李斌,吴泽兵,等.单齿静压入试验破碎坑的数据处理及几何建模[J].岩石力学与工程,2000,19(3):373－375.YANG Ying-xin,LI Bin,WU Ze-bing,et al.Geomtric modeling and data processing of craters from static indenting tests by single insert[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(3):373－375.

[16]古剑飞.牙轮钻头牙齿破岩机制研究[D].成都:西南石油大学,2008.

[17]杨迎新,林敏,张德荣.牙齿刮切试验破碎坑的几何建模[J].岩石力学与工程,2002,21(9):1392－1394.YANG Ying-xin,LIN Min,ZHANG De-rong.Geometric modeling of rock grooves induced by scraping tests with single insert[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(9):1392－1394.

[18]HAGAN J T.Cone crack around Vickers indentations in fused silica glass[J].Journal of Materials Science,1979,14:462－466.