含空洞地层中双线盾构施工引起的土体位移研究

2022-04-20戴子涵魏纲齐永洁

低温建筑技术 2022年3期

戴子涵，魏纲，齐永洁

（1.浙大城市学院土木工程系，杭州 310015；2.浙江大学建筑工程学院，杭州 310058）

0 引言

地下空间土体条件复杂，以空洞为代表的常见不良地质体常见于浅地层，再加之城市中地铁隧道常采用双线平行盾构施工的方法来提升地下空间的利用率，加重了对土体的扰动［1］，对周边建筑物以及邻近的地下工程与管线的安全造成了极大的威胁。因此，研究含空洞地层中双线盾构施工引起的土体位移预测方法具有重要意义。

针对含空洞地层中双线平行盾构施工引起的土体位移问题，国内外现有的研究方法与成果极少。目前已有研究大多只针对双线盾构或含空洞地层进行单独研究。针对双线盾构的研究，研究方法主要包括理论分析［2］、数值模拟［3］以及现场监测［4］。从只考虑土体损失的情况扩展，逐渐形成了可以将土体损失、正面附加推力、盾壳摩擦力、附加注浆压力等多因素纳入计算的体系。针对含空洞地层的研究，研究方法主要包括数值模拟［5-7］、模型试验法［8，9］及理论计算法［10-13］，研究内容主要集中在空洞变形发展引起地表塌陷的破坏机理［14，15］、空洞存在对隧道管片受力及破坏模式的影响、空洞和隧道共同影响下的地表沉降规律［16］、含空洞地层应力场变化规律等。其中，杨公标等采用Schwarz交替法原理和复变函数理论求得了地表沉降，但其将模型简化为二维平面，需繁琐编程计算的同时只计算地表沉降，Cui Yunliang等推导了含空洞地层中盾构开挖引起的土体变形三维解，但其仅考虑了单线盾构开挖过程中的土体损失作用，没有考虑多因素影响及双线盾构隧道。因此需进一步研究含空洞地层中，双线盾构在多因素影响下施工引起的土体变形规律。

文中引入空洞收敛率的概念来表示空洞的收敛大小，推导了空洞单独收敛变形造成的上部土体位移计算公式；考虑盾构施工对空洞的变形及移动影响，推导了含空洞地层中双线盾构施工引起的土体三维变形计算公式；结合算例分析，对多个单因素作用下的土体变形及地表沉降进行计算，研究了相关的变化规律。

1 土体位移研究

1.1 研究思路

文中方法主要包含以下的步骤：①建立理论计算模型；②计算多因素影响下双线盾构施工引起的土体位移值；③在考虑空洞整体结构位移的情况下，计算空洞收敛引起的土体位移值；④基于叠加原理［17］，将步骤②和③的土体位移值叠加，即可求得土体总的位移值。

1.2 文中计算模型

图1（a）为文中理论计算模型图，图中假设双线隧道沿x轴方向掘进且关于xoz平面对称，隧道半径为R，隧道轴线埋深为H，空洞半径为Rs，中心埋深为h1。图1（b）为文中计算模型断面图，图中双线隧道间距为J。

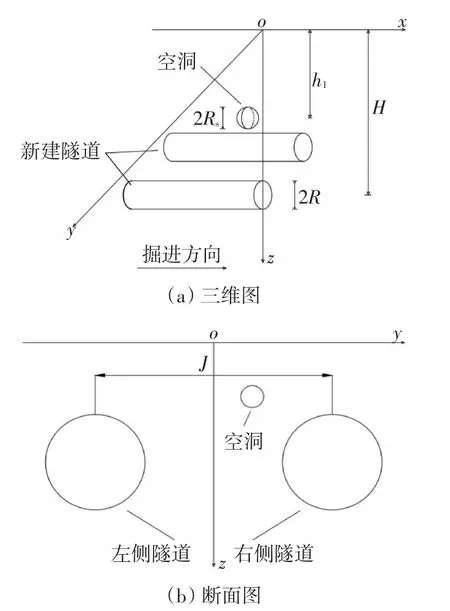
图1 计算模型图

1.3 双线盾构隧道开挖引起的土体位移计算

参照魏纲等［18］的研究成果：①盾构正面附加推力引起的土体竖向、水平位移为v1、w1；②盾壳与土体之间的摩擦力引起的竖向、水平位移为v2、w2；③附加注浆压力引起的竖向、水平位移为v3、w3；④土体损失引起的竖向、水平位移为v4、w4。

则双线盾构隧道施工引起的土体竖向位移v与水平位移w：

限于篇幅，具体公式不具体展开，详见原文献。

1.4 空洞变形引起的土体位移计算

1.4.1 基础理论的介绍

文中在研究过程中，假设隧道开挖前空洞已经产生且自身保持稳定结构［19］，不考虑在隧道施工前因空洞产生的地表及土体变形。认为隧道开挖对空洞的影响，主要包括空洞边界的收敛变形和空洞结构的整体移动。其中空洞的边界收敛模式又包括形状收敛和收敛中心偏移，为有效估算空洞收敛及移动所引起的地表沉降及上部土体位移，文中采用均匀收敛模型进行计算。空洞的整体移动则受隧道开挖影响，与空洞和隧道的相对位置有关。

基于随机介质理论及齐静静等［3］的研究成果，空洞收敛变形引起的上部土体最终沉降体积应等于土体损失体积。d在空洞内任取一个埋深为η的计算单元体积为dξdζηdζη，开挖单元完全塌陷引起的上部任意一点（x，y，z）土体在沿x、y、z轴方向上的位移值dU-x、dU-y、dU-z：

式中，β为空洞上部土体的主要影响角；r（z）为z方向上的影响半径。

在此基础上，对参数β进行了优化，考虑了tanβ随开挖单元深度h变化的情况。

式中，m的取值为0.45～0.5。

1.4.2 文中计算公式的推导

椭球形空洞沿x轴、y轴、z轴3个方向上的半径分别为Ra、Rb、Rc，在椭球形空洞内部任取一计算单元dV=dξdζdη，计算单元的埋深为η。如图2所示，在双线盾构施工的影响下：①假设空洞首先发生形状上的收敛，采用等比例均匀收敛模型，其沿x轴、y轴、z轴3个方向上的半径将减小为Ra'、Rb'、Rc'；②其次空洞产生整体移动，空洞中心点o1将会移动至o2，竖向、水平位移为Δz、Δy。

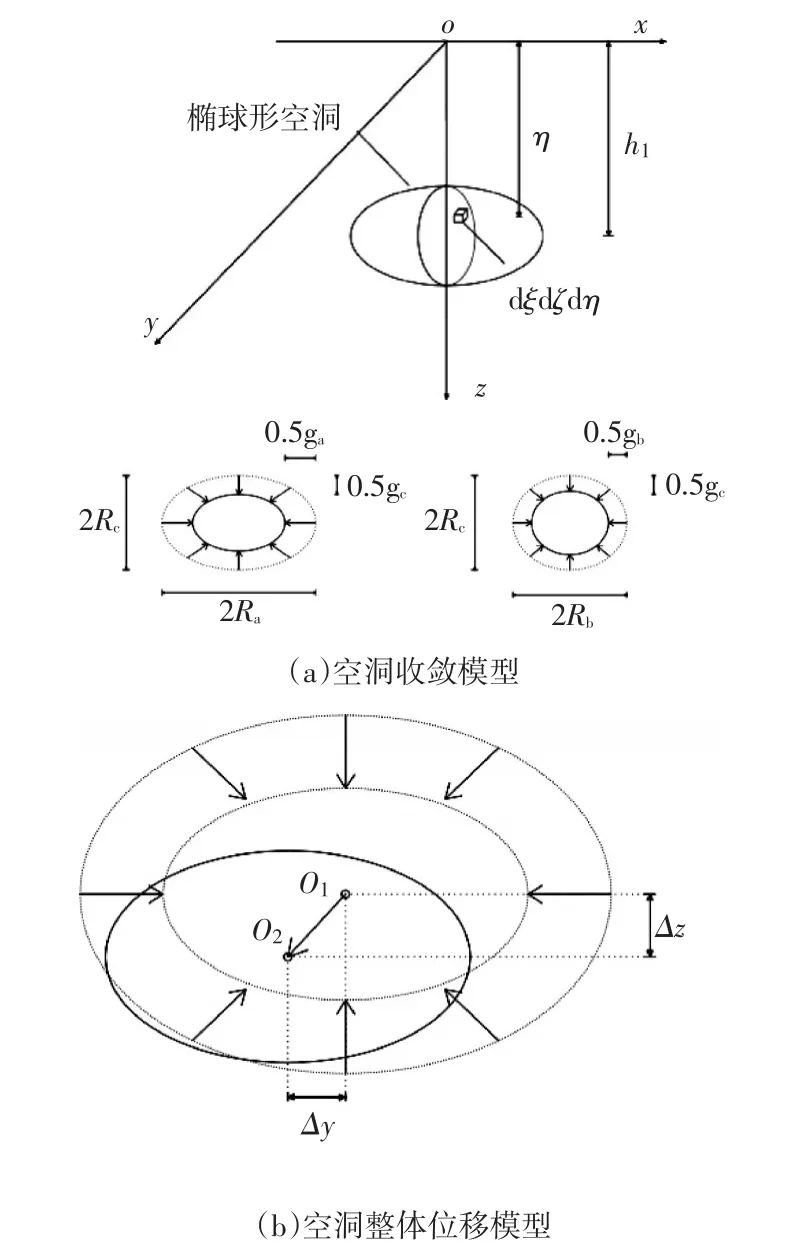
图2 椭球形空洞收敛及整体位移模型

依照文中的方法，对初始空洞边界和最终空洞边界范围内的计算单元分别进行积分，再将两部分的计算结果相减，即可得到椭球形空洞收敛变形引起的周围土体沿x轴、y轴、z轴的变形Ux-q、Uy-q、Uz-q为：

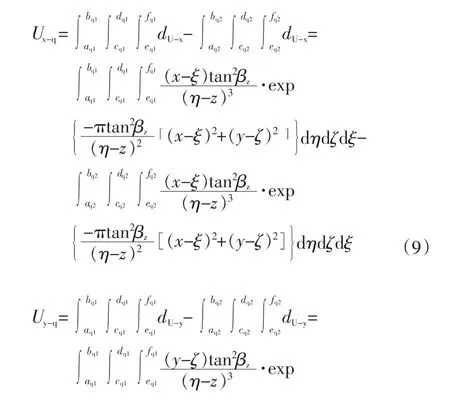
式中，a、b为变量ξ（沿x轴）的积分上下限；c、d为变量ζ（沿y轴）的积分上下限；e、f为变量η（沿z轴）的积分上下限；下标q1和q2分别代表椭球形空洞收敛变形前和变形后；各积分上下限计算公式如下：

1.4.3 计算参数取值方法

空洞收敛后的轴半径Ra'、Rb'、Rc'与空洞收敛率εs相关。空洞作为一个隐伏腔体，其收敛率在实际工程中难以测量。文中参照Loganathan（1998）［22］的研究成果，认为εs可根据与隧道的相对位置及隧道开挖土体损失率ηs进行估算，即满足：

式中，（ys，zs）为空洞中心点坐标。

均匀收敛模式下椭球形空洞在x轴、y轴、z轴按照等比例缩小，3个方向上的径向缩小量ga、gb、gc分别需要满足：

椭球形空洞收敛后的半径Ra'、Rb'、Rc'为：

为有效计算空洞的整体位移，参照文中提到的方法，将空洞中心点o1的坐标代入计算，即可得到土体中o1点位置的竖向位移Δz与水平位移Δy。由于土体具有连续性，文中近似认为该方法计算得到的位移即为空洞的整体位移。

1.5 含空洞地层中双线盾构施工引起的土体位移计算

采用叠加原理，由式（1）、式（2）、式（10）、式（11）得到含空洞地层中双线盾构施工引起的土体竖向位移Uz与水平位移Uy：

2 算例分析

2.1 算例介绍与分析

文中假定双线盾构埋深、尺寸、走向相同，参考杭州地区实际工程案例数据，假定计算参数如下：盾构机长度为8m，R=3m，H=15m，J=12m，同步注浆长度为10m。右侧隧道先开挖，计算土体损失率为0.5%，可计算得到左侧隧道计算土体损失率约为0.14%。两台盾构机正面附加推力p1f=p1s=20kPa，盾壳与土体的摩擦力p2f=p2s=30kPa，附加注浆压力取p3f=p3s=50kPa；Rs=1m，h1=6m，空洞中心位于双线隧道中心线上，且εs=8%。

图3为地表沉降曲线示意图，图中纵坐标负值代表地表沉降。由图可知，地表总沉降最大值位于y=0处，为26.95mm。仅考虑土体损失时右侧土体沉降要大于左侧的土体沉降，这是由于右侧隧道的计算土体损失率要大于左侧隧道的计算土体损失率，导致曲线偏向于右侧，并在图3的（-12m，12m）区间中表现出来，而（12m，30m）区间的沉降量却要小于（-30m，-12m）区间。右侧的曲线相较于左侧曲线更为陡峭，使得土体沉降值关于中心逐渐呈现出左侧大右侧小的规律。

图3 地表沉降曲线（x=0m）

图4 为沿掘进方向地表土体沉降曲线对比示意图，正面附加推力引起的地表土体沉降曲线沿开挖面所在轴线负对称，盾构前方未开挖土体会在正面附加推力的作用下向上隆起，而盾构后方土体会沉降，最值约为±0.84mm，约在x=±12m处；盾壳与土体摩擦力引起的地表土体沉降曲线沿掘进方向上盾构机中心所在轴线负对称，盾构前方土体会在盾壳与土体摩擦力的作用下向上隆起，盾构后方土体会沉降，最值约为±2.89mm，约在x=6m和x=-12m处，盾壳与土体摩擦力引起的地表土体沉降曲线与正面附加推力引起的地表土体沉降曲线趋势相近，但盾壳与土体摩擦力会对土体产生更大的扰动；注浆附加压力引起盾构后方土体向上隆起，最值约为3.71mm，约在x=-13m处；土体损失引起的土体沉降由盾构前方至后方逐渐增大，且逐渐接近极限值，约为-10mm。算例中开挖面后约6m之后，土体损失引起的地表土体沉降与多因素共同影响下引起的地表土体沉降较为接近，而在开挖面后约6m之前，尤其在正面附加推力、盾壳与土体摩擦力的显著影响区附近，土体损失引起的地表土体沉降与多因素共同影响下引起的地表土体沉降区别较大。因此，传统的只考虑土体损失引起的土体沉降的计算方法，存在一定缺陷；文中方法能有效地考虑正面附加推力、盾壳与土体摩擦力以及注浆附加压力对土体产生的影响。

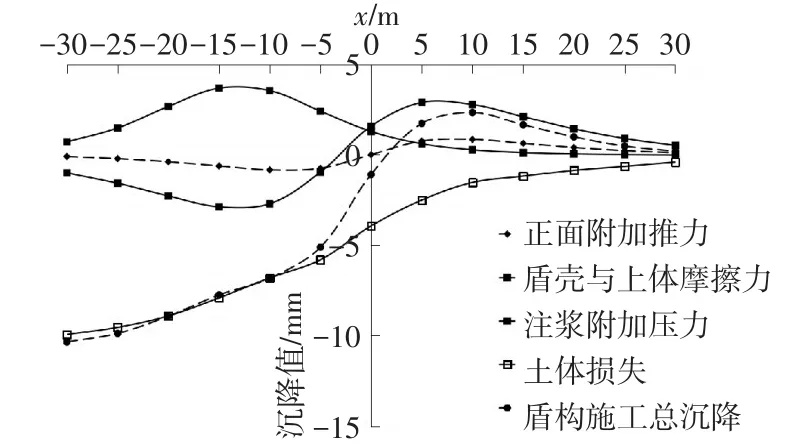
图4 沿掘进方向地表土体沉降曲线对比（y=0m）

图5为地表沉降沿x轴的分布规律示意图，整体趋势为沉降随着x的增大而变小，x越小，盾构通过的距离越远，所造成的影响越完全，当离开开挖面距离逐渐增大时，总沉降趋于稳定。曲线在（-10m，2m）出现了较为明显的下凹，该部分沉降值相较于曲线行走趋势产生了明显增大，该部分沉降量偏大是由空洞导致的。而（2m，8m）处并未产生明显的下凹，甚至产生了较大的隆起，是由于土体在正面附加推力、盾壳与土体的摩擦力作用下产生隆起，在x=10m处之后，土体逐渐离开了各个因素的影响范围，土体隆起逐渐降低，渐趋于0。

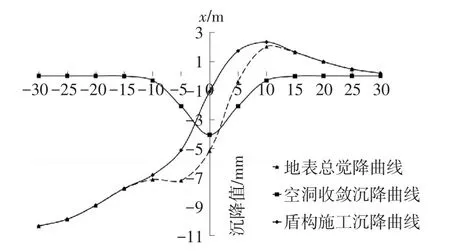
图5 地表沉降沿x轴的分布规律（y=0m）

图6为土体沉降沿z轴分布规律示意图，土体沉降随埋深的增加而逐渐增加，接近地表时增加较为缓慢，当逐渐靠近空洞上边缘时，土体沉降迅速增大，直至达到最大值。x=0时，土体沉降最大值为-109.89mm，发生在空洞上边缘位置；x=-5m时，土体最大沉降值为-23.22mm，发生在隧道上边缘埋深处，在深度为2～5m的区间段，土体沉降相对于整体曲线要偏大，这是由于空洞收敛的作用，显著增大了这一部分的土体位移；x=-10m时，土体沉降最大值为-29.82mm，发生在隧道上边缘埋深处，x=-10m时沉降曲线并未像x=0时一样包含沉降值突变段，是由于x=0时计算极限点位于空洞边缘，应力介质产生突变，而x=-10m时计算点位置没有隧道，土体均匀连续，因而不会产生突变。

图6 土体沉降沿z轴分布规律（y=0m）

2.2 不同因素对地表沉降的影响

2.2.1 空洞半径改变对地表沉降的影响规律

选用了7种不同半径的空洞，半径为0.2～1.4m，每0.2m取为一个工况。图7为空洞半径改变对地表沉降的影响对比示意图。这7种工况中，地表沉降最大值均出现在y=0处，空洞半径为0.2m的工况中地表最大沉降值最小，为-3.15mm，空洞半径为1.4m的工况中地表最大沉降值最大，为-14.14mm，在算例中，空洞半径由0.2m增加到1.4m的过程中，地表沉降增大了约11mm，增幅约为349.21%。

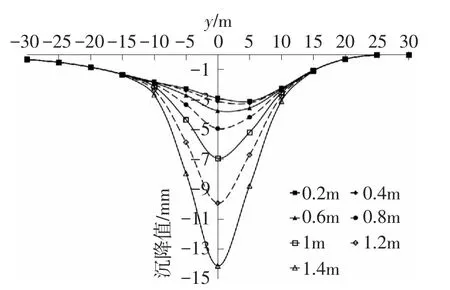
图7 空洞半径改变对地表沉降的影响对比（x=0m）

2.2.2 空洞中心埋深改变对地表沉降的影响规律

文中选用7种不同的中心埋深工况，为3～9m，每1m取为一个工况。图8为空洞中心埋深改变对地表沉降的影响对比示意图。如图8所示，各个工况中最大沉降量都出现在y=0m处，随着空洞埋深的逐渐增大，最大沉降量逐渐减小。空洞埋深为3m时，最大沉降量约为-19.62mm，空洞埋深为9m时，最大沉降量约为-4.68mm。

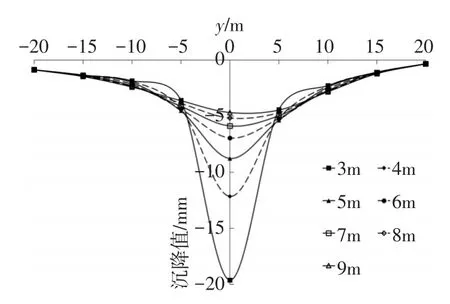
图8 空洞中心埋深改变对地表沉降的影响对比（x=0m）

2.3 空洞位置改变对地表沉降的影响规律

由于文中已研究过空洞中心埋深改变对地表沉降的影响，因此仅考虑空洞坐标中x与y的改变对地表沉降的影响。分别取y为-12、-8、-4、0、4、8、12m。

图9为y坐标改变对地表沉降的影响对比示意图，沉降槽中心位置随着y的增大而逐渐右移，最大沉降值出现在y=4m的曲线而非y=0的曲线中，由于隧道与空洞的共同作用，沉降曲线向空洞所在侧产生了一定的偏移。在y=-12m的曲线中，出现了两个较为明显的沉降槽，是由于空洞距离右线隧道较远，产生的沉降较为独立，而在y=12m的曲线中并未出现两个较为明显的沉降槽，是由于左线隧道的计算土体损失率较低，沉降不明显。在空洞越靠近y=0m时，曲线趋于光滑，贴近正态分布曲线。

图9 y坐标改变对地表沉降的影响对比（x=0m）

分别取x为-12、-8、-4、0、4、8、12m。图10为x坐标改变对地表沉降影响对比示意图，地表沉降槽随着x的增大逐渐右移，且空洞位置越靠近开挖面，沉降曲线越平缓。总体来看，空洞的存在会加剧其附近土体的沉降，使得空洞附近的曲线沉降值增大，在x趋于盾构前方或后方较远位置时，各条曲线趋于平缓且一致，空洞x坐标越小，则越迟汇入后方平缓曲线，越早汇入前方平缓曲线。空洞x坐标越小，则开挖面后方最大土体沉降值越大，开挖面前方最大土体隆起值越大。