桩基冻胀力的三维黏弹性问题研究

何 菲，王 旭，蒋代军，梁庆国，任明洋

（兰州交通大学 土木工程学院，甘肃 兰州 730070）

1 引 言

冻胀是冻土工程中普遍存在的力学现象，寒区轻型建筑物基础由于切向冻胀力的作用，出现冻胀变形问题，基础断裂或拔起破坏也时有发生，造成了巨大的经济损失。在设计中选取正确的切向冻胀力一直是建筑实践中特别考虑的问题之一。

多年来，我国的科研人员在基础冻胀方面进行了大量的研究，获得了较为丰硕的研究成果。早期的研究主要采用试验的方法研究冻胀力的大小、沿深度的发展规律以及沿基础表面的分布，其目的是为了制定冻土地区建筑物基础的设计与施工规范[1－3]。由此得出了一些经验公式及相关规范，但是由于影响地基土冻胀性的因素非常复杂，包括土质、水分、温度、压力等，又因试验场地的多样性，试验结果离散性较大。关于桩基冻胀的计算理论随之发展起来。周有才[4]假定桩侧土体的约束冻胀量曲线为幂函数，提出了简化的Linell 和Kaplar 公式，用基础约束范围内冻胀减少体积与冻胀地基系数的关系计算了冻胀力。赖远明等[5]提出，切向冻胀力与冻结强度有本质的区别，利用叠加原理和弹性半空间的Mindlin 公式，导出了计算桩基冻胀力三维问题的积分方程。李洪升等[6]把冻土层简化为半平面体（或半空间体），将基础影响简化为作用在弹性体表面的集中力或分布力，采用弹性理论导出冻土层沉陷量的计算公式。徐学燕等[7]利用有限差分方法求解自由冻胀量与约束冻胀量之差即为场地最终的冻胀量。

综上所述，关于桩基冻胀研究已经取得了很多的成果，但是目前的研究工作大多基于弹性理论。实际上，地基土体远不是理想的均质弹性体，故将弹性理论公式应用到地基上来，总是带有近似性。而且冻胀力随时间的发展变化又无法真实测定，切向冻胀力何时达到最大，对工程的影响又是如何等都是需要考虑的问题。为此，本文在已有文献基础上，从分析地基土冻胀变形的规律开始，运用叠加原理和弹性半空间的Mindlin 公式[8]，并结合经典黏弹性力学理论，通过理论推导，对桩基冻胀力三维黏弹性问题提出了合理的表达式及解释，结合工程实例进行编程数值计算和验证，得出了冻胀力随时间和空间变化的三维曲面。

2 冻土与桩基相互作用的力学模型

在负温条件下天然土体冻结产生的冻胀，称为自由冻胀。寒区工程中由于桩基础的作用，使桩基周围地基土的冻胀受到约束，即发生所谓的约束冻胀，约束冻胀是一种非均匀冻胀。约束冻胀对地基的影响有一定的约束范围，在靠近桩基础的一定范围内土体的自由冻胀受到约束，范围外则发生自由冻胀。一般地，对于一个完全锚固的基桩，其有效影响范围为基础直径的7 倍[9]。此外，约束冻胀还受到基础形状、土体与桩的接触面面积和冻结强度、土的冻胀特性以及冻结深度等因素的影响[6]。土的自由冻胀和约束冻胀如图1 所示。

关于自由冻胀量的研究，不管是在微观、冻胀机制还是现场原位观测，都取得了较为系统的研究成果[10－11]。根据叠加原理就可以得到约束冻胀变形，如图1 所示，认为桩周土的约束冻胀是先发生自由冻胀，然后在自由冻胀基础上由冻胀地基对桩基的反作用力引起的变形，两种冻胀的叠加产生了约束冻胀地表。

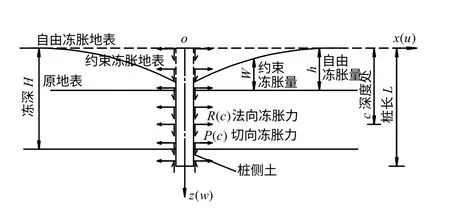
图1 自由冻胀和约束冻胀示意图Fig.1 Free frost heave and restrained frost heave

3 半空间土体内部作用集中力的黏弹性解

为了便于研究，在进行理论分析之前，首先对半无限空间土体作如下假设：

（1）假定地基土是线性黏弹性介质；

（2）假定地基土是均匀各向同性的连续变形体，在深度和水平方向上无限延伸，即为半无限体；

（3）土体在外部集中力作用下的应力为三维应力状态，应力球张量和应变球张量之间符合弹性关系，而应力偏张量和应变偏张量之间为黏弹性应力-应变关系。

由于冻土的变形特性具有蠕变和松弛效应，而Kelvin 模型无法描述松弛效应，又考虑到为便于计算，故假定偏张量之间符合三参量固体模型。

依据半无限弹性体内部作用有竖直向或水平向集中力的Mindlin 弹性解，根据准静态黏弹性-弹性相应原理，结合Laplace 变换及Laplace 逆变换，求解相应的三维线性黏弹性解答[12－13]。半无限体内在点（0,0,c）处作用一沿z 轴方向的单位集中力时，任意点M(r,z)在 t 时刻的竖向位移和水平向位移分量的黏弹性表达为

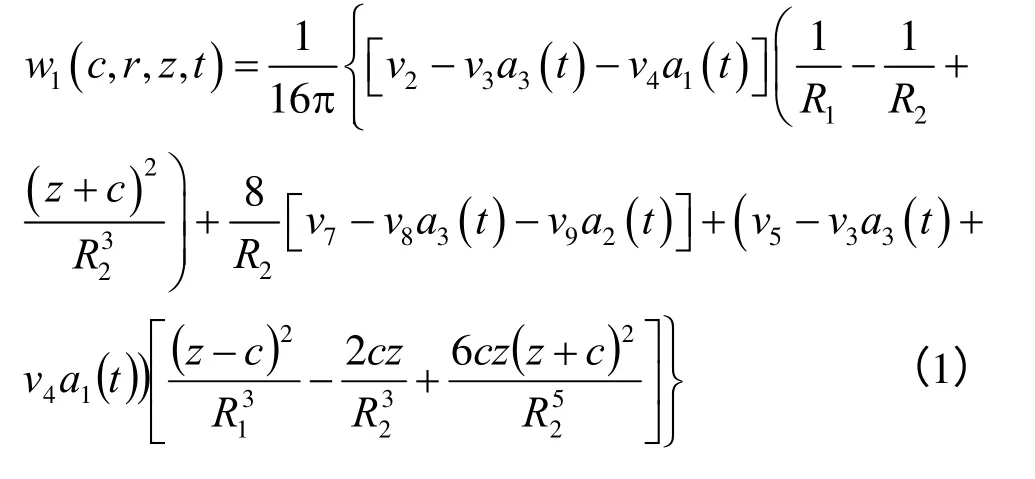
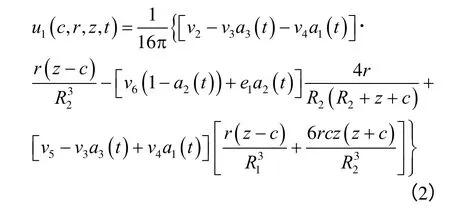
半无限体内在点(0,0,c)处作用一沿x 轴方向的单位集中力时，任意点M(x,y,z)的位移分量的黏弹性表达如下：

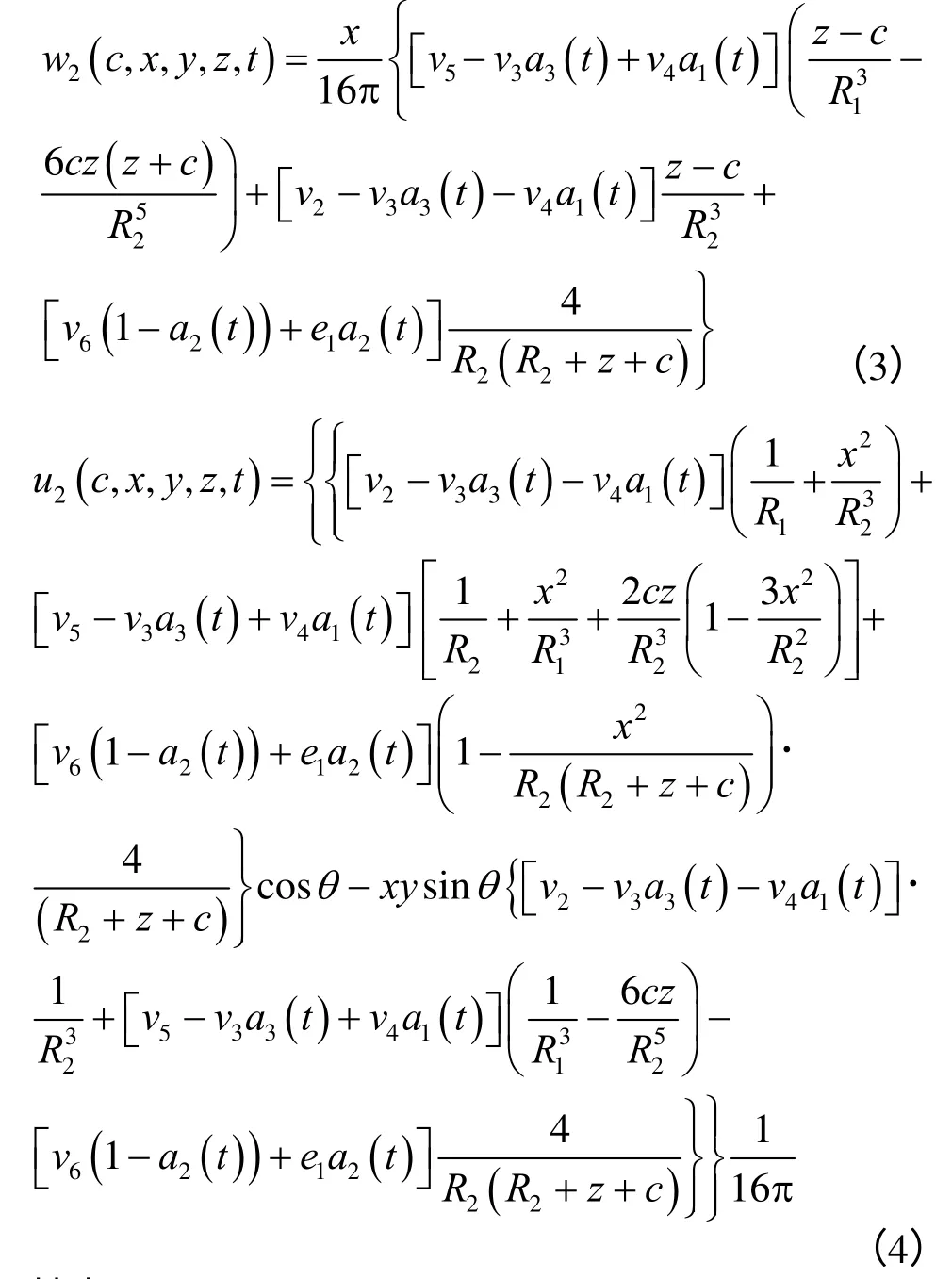
其中：

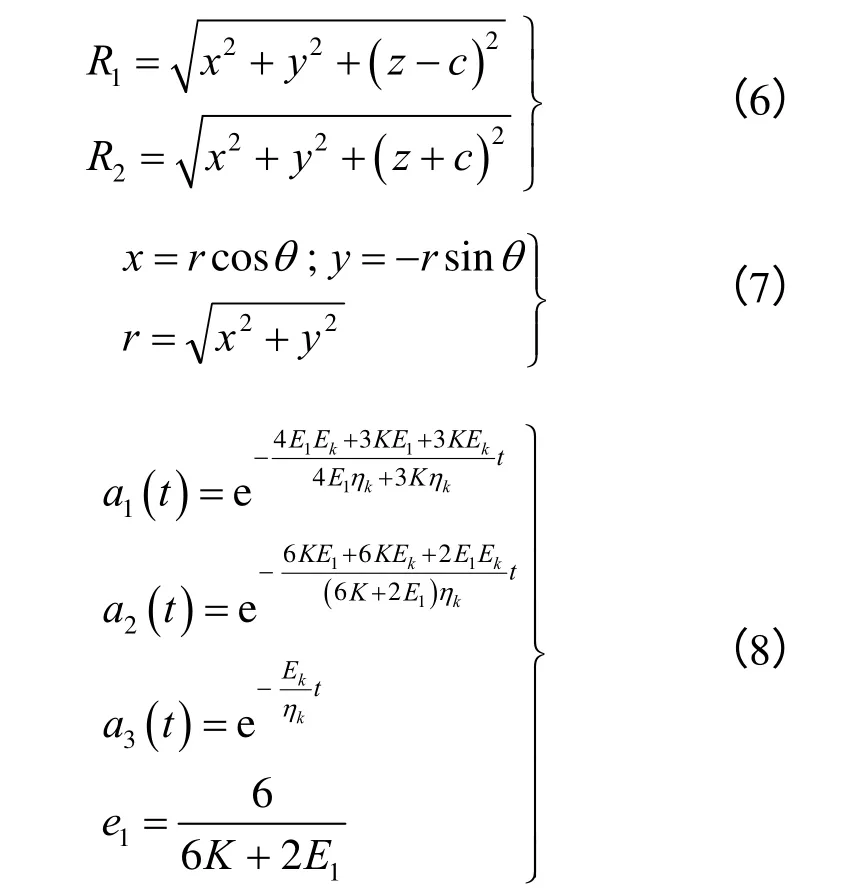
式中：K为体积弹性模量；E1、Ek、ηk分别为三参量固体模型系数。

4 桩基冻胀力分布的黏弹性理论计算公式

4.1 自由冻胀产生的土体位移

取自由冻胀地表线和桩基轴线交点为坐标原点o，坐标轴oxyz 如图1 所示（y 轴垂直纸面向外）。模型中冻深以下部分为融土，理论计算时冻深以下部分桩基与桩侧土体之间按摩阻力计算。在本文计算中，融土、冻土的弹性模量及黏性系数采用等效模量和等效系数计算。

自由冻胀产生的土体位移与冻深H(t)和自由冻胀量h(t)有关[5]，表达式如下：

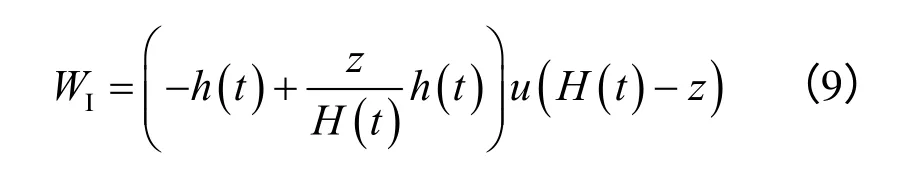
式中：u为阶跃函数，其值为

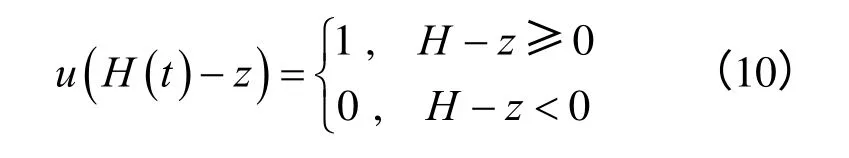
4.2 约束冻胀产生的土体位移

土体冻胀产生对桩基的切向冻胀力P(c)和法向冻胀力R(c)，土体则受到桩基的反作用力，产生约束冻胀位移。利用式（1）和式（2），在沿桩身分布的切向冻胀反力作用下任意点M(r,z)的竖向位移WII和UII可表示为

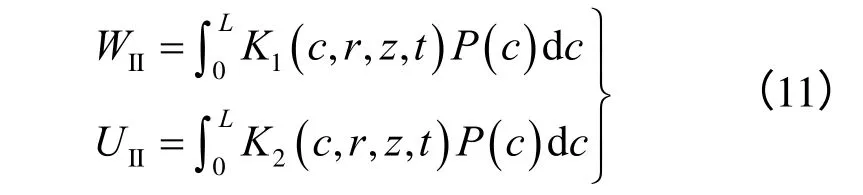
由式（1）、（2）可得

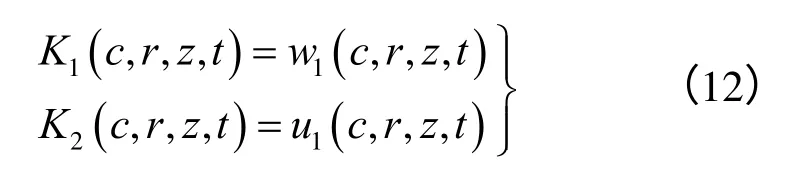
法向冻胀反力沿桩侧分布，方向背离桩侧。对于竖直平面（xy 平面）而言，平行于x 轴的单位法向冻胀反力由一对集中力组成，设定其中一力沿x轴正向作用于(0,0,c)，则另一力等值反向作用于(-d,0,c)，d为桩的直径。利用式（3）、（4），在这样一对集中力共同作用下，任意点M(x,y,z)的位移为

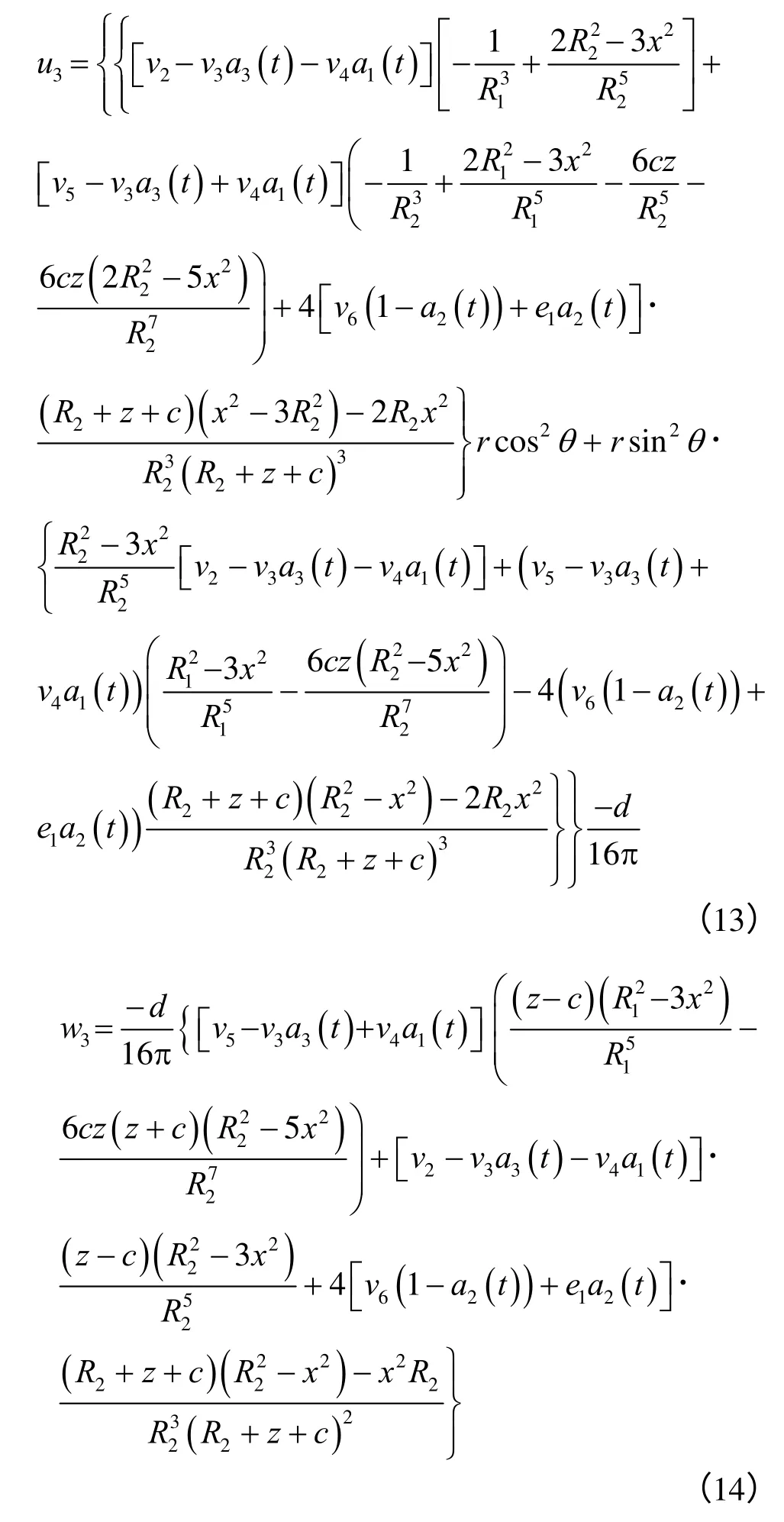
将桩基对冻土的径向作用力R(c)分别乘以式（13）和式（14），并沿环向积分，便得到在xy 平面内z=c 处作用环向均匀分布的冻胀反作用力时，半空间土体内任意一点M(r,z)的位移表达式为

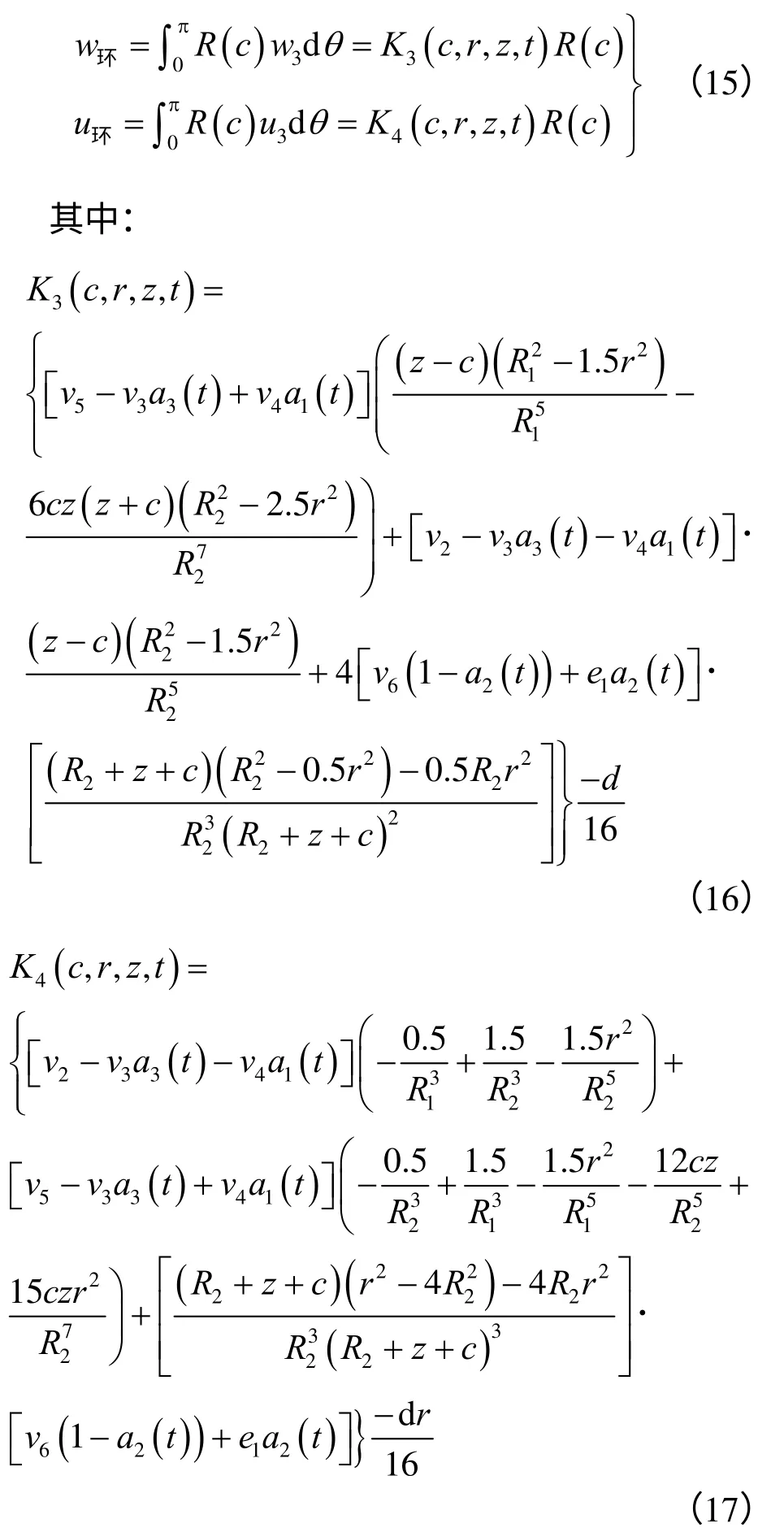
则在埋入土体的桩长范围内(z∈0,L)分布的冻胀反作用力作用下，冻土任意一点M(r,z)的位移为

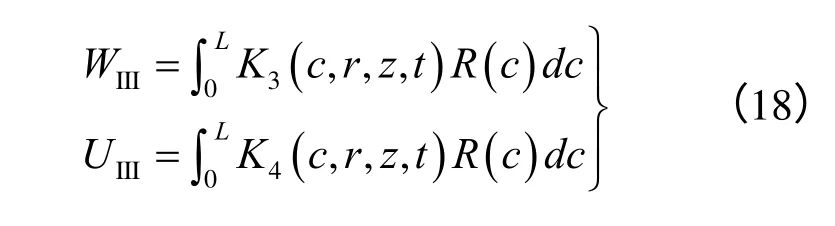
由叠加原理便可得到约束冻胀产生的位移。利用式（9）自由冻胀产生的位移、式（11）切向冻胀力产生的位移和式（18）法向冻胀力产生的位移，得到在切向冻胀力P(c)和法向冻胀力R(c)作用下冻土内任意一点M(r,z)的位移为

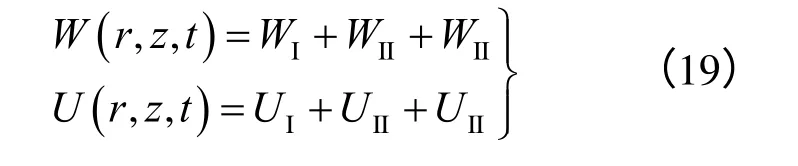
式中：UI为桩侧土自由冻胀时沿水平方向产生的位移。

4.3 验证

为了验证上述理论推导的正确性，以式（14）为例，将t=0 代入式（14），得到在t=0 时刻一对集中力作用在点(0,0,c)和点(-d,0,c)处时任意点M(x,y,z)产生的竖向位移为

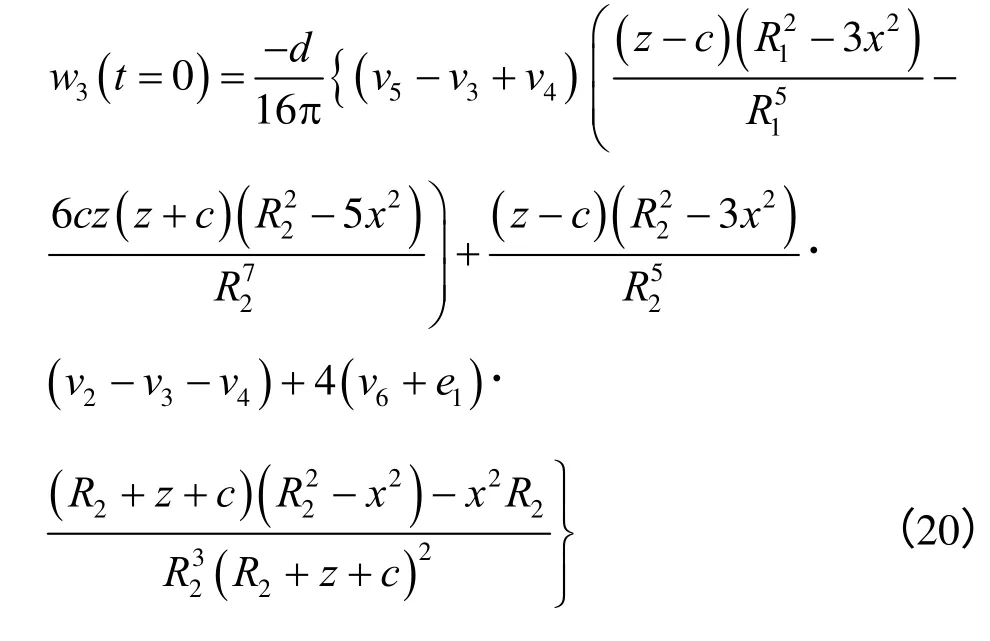
式（20）与弹性解[5]相同，表明在加载瞬时材料的变形主要由三参量模型中弹簧E1来承担，由此也可以验证本文的黏弹性理论解的正确性。

4.4 桩基冻胀力的黏弹性解

土体冻胀后，桩侧土与桩基黏结在一起无相对滑动，可认为其水平位移为0；由于钢筋混凝土桩的弹性模量比冻土的大得多，可假设桩身不可压缩，则桩侧土体竖向位移等于桩的拔出量hb(t)。若计算初始时刻为冻胀前，则桩侧土水平位移不为0，用m 表示。因此，可以将式（19）简化为关于切向冻胀力和法向冻胀力的方程组，并将式（19）中的方程式离散化处理得到tk时刻的冻胀力方程为

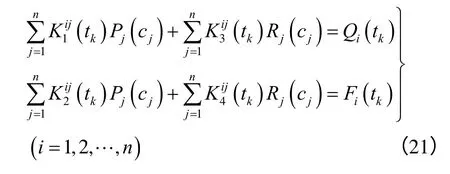
式（21）中，埋入土体中的桩长L 划分为n 等份，每段长ΔL =L/n，且有

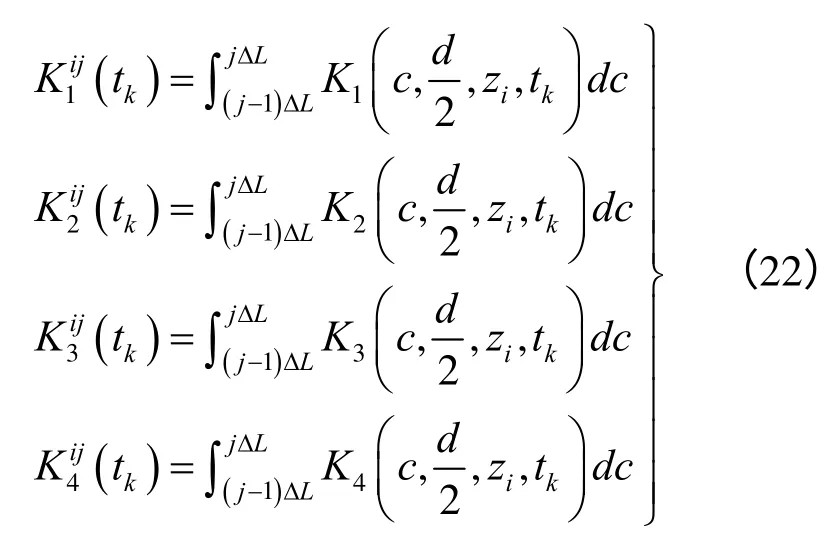
求解时将式（21）转化以下矩阵形式进行计算：

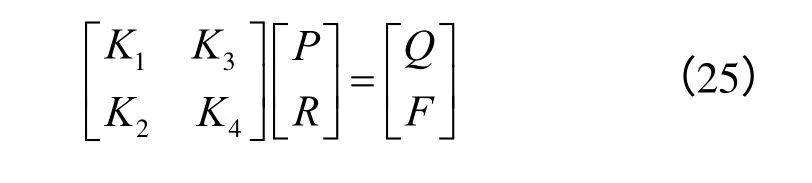
由冻胀反力与冻结强度的关系可知，冻胀反力的最大值等于冻结强度，也就是说，冻胀反力达到或超过冻结强度时，冻土与基础联接界面被剪坏，基础也就对冻土没有了约束作用[14]。因此，如果由式（25）计算出来的切向冻胀反力大于桩土间的冻结强度，需用桩土表面的摩阻力修正式（25），并将系数矩阵降维处理计算，直到计算出的切向冻胀力均小于冻结强度为止。

5 算 例

某钢筋混凝土灌注桩基础[5]直径d=0.3 m，埋深L=2.5 m，地基土质为砂质黏土，冻深H=2 m，桩基拔出量hb=0.01 m，自由冻胀量h=0.192 m。计算时以该状态为初始时刻进行研究。

计算分析时，关于冻土三参量模型中E1、Ek、ηk三个系数能查阅到的资料很少，故由室内实测冻土蠕变曲线反演得到。本蠕变试验的围压为0.5 MPa，温度为-1.5 ℃，蠕变应力为1.316 MPa。根据试验结果，据三参量模型蠕变解公式为

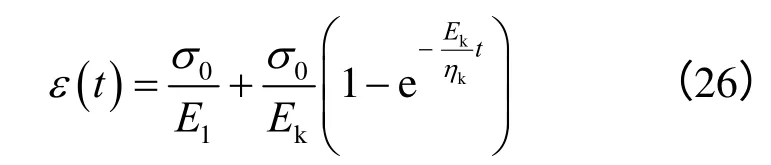
利用单纯形法，寻优求解非线性方程组，得到3 个参数的取值为E1=93.96 MPa、Ek=23.09 MPa、ηk=8.08 MPa ⋅ d。

自由冻胀量、冻深以及桩基冻拔位移随时间的发展变化关系，由已有资料得到。其中自由冻胀量与冻深的变化遵循海拉尔冻土站1974、1975年度冻结过程线的规律[14]，桩基冻拔位移规律由孙洪伟等[15]关于桩基冻拔位移的实测值拟合得到，并结合本算例中的自由冻胀量值、冻深值以及桩基上拔量，最终得到其随时间的发展变化关系分别为

按照本文建立的桩基冻胀力三维黏弹性方程得到的初始时刻切向冻胀力及法向冻胀力随深度的变化曲线如图2、3 所示，其中取冻结强度为200 kPa，用于对切向冻胀力的修正计算。与文献[5]提供的数据相比（如图4 所示），冻胀力的分布规律与本文理论计算结果基本一致。本文的切向冻胀力最大值在桩深1.0 m 处，文献[5]中最大值在0.8 m 附近，两者相接近，表明本文建立的桩基冻胀力三维黏弹性方程计算模式是可行的。就数值而言，本文计算结果与弹性解存在一定的差别，这是由于黏弹性解模型中参数数目多于弹性解模型，而且两种模型的参数取值也存在差别。

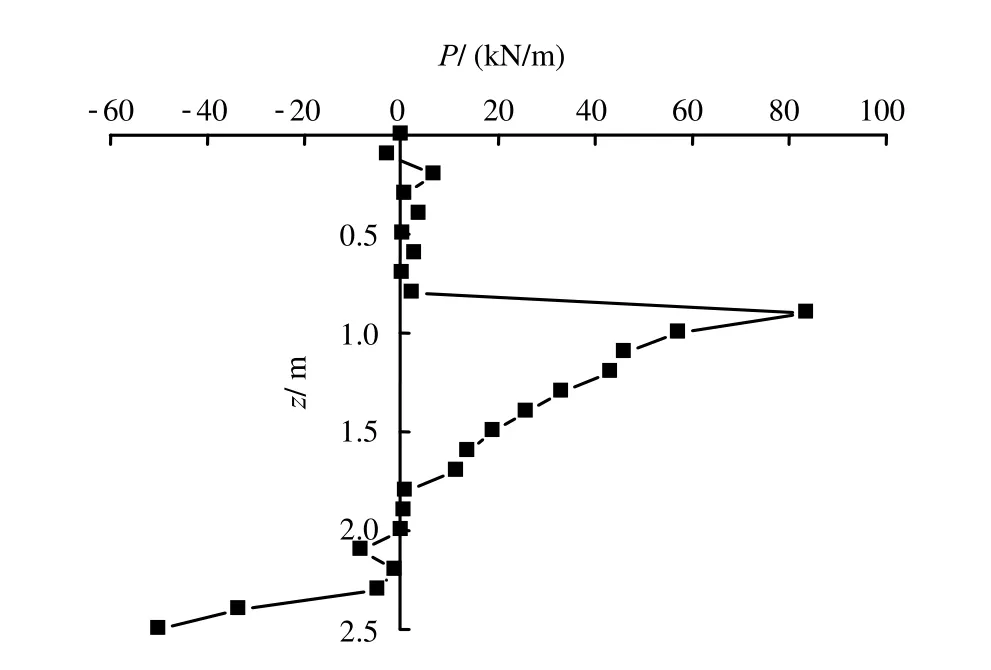
图2 初始时刻切向冻胀力沿桩深的分布Fig.2 Distribution of tangential frost forces along the lateral surface of pile at the initial time

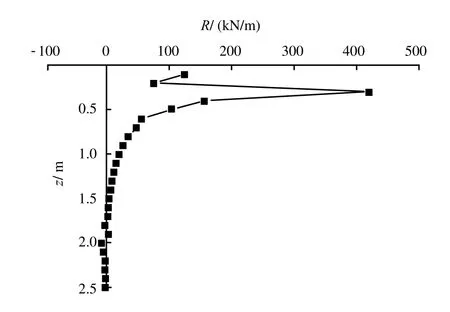
图3 初始时刻法向冻胀力沿桩深的分布Fig.3 Distribution of normal frost forces along the lateral surface of pile at the initial time

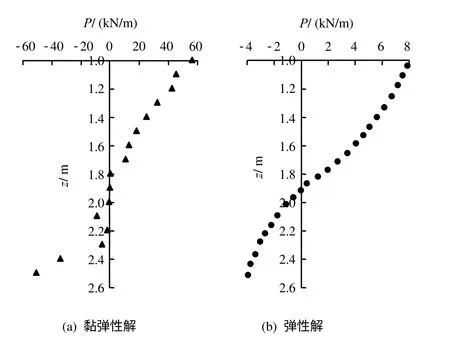
图4 切向冻胀力弹性解和黏弹性解Fig.4 Viscoelastic and elastic solutions of tangential frost force

已有文献中关于冻胀力理论计算值随时间变化的研究鲜有见到。本文根据前述理论分析，得到本算例中切向冻胀力、法向冻胀力时空分布的三维曲面，如图5、6 所示。计算所选取的冻结深度模型中当冻结到30 d 时，冻结深度已达到2.4 m，接近桩底，故只研究冻结30 d 的情况。

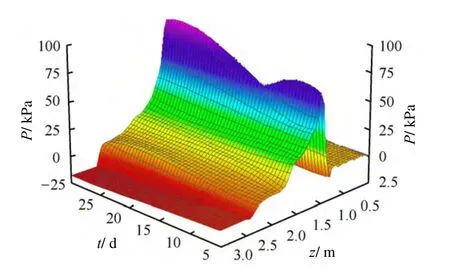
图5 切向冻胀力随深度及时间的三维曲面Fig.5 3D surface of tangential frost forces vs.depth and time

由图5 可以得出，随着冻结时间的增长，冻结深度逐渐增大的同时，切向冻胀力峰值位置缓慢地下移，峰值也在增大，冻结30 d 后的切向冻胀力峰值比冻结5 d 时的值增大了约1/3。由图6 可知，法向冻胀力分布范围随时间的增长而增大，其峰值随时间变化较小。从法向冻胀力峰值来看，图6 所示的峰值比图3 所示初始时刻的冻胀力峰值小很多，这是由于计算时认为初始时刻桩侧土体与桩体有一定距离，土体冻胀后，桩侧土与桩基黏结在一起无相对滑动，其水平位移为0。

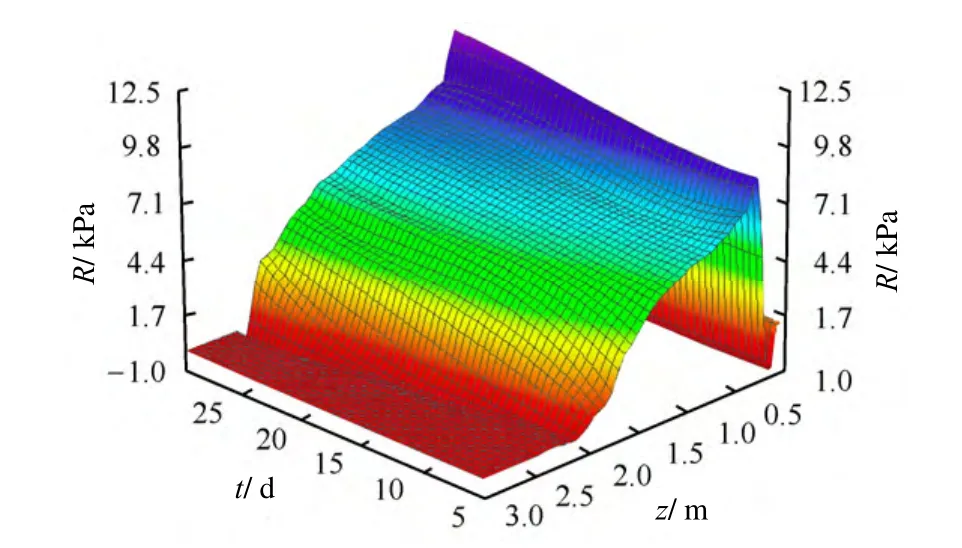
图6 法向冻胀力随深度及时间的三维曲面Fig.6 3D surface of normal frost forces vs.depth and time

6 结 论

（1）以桩基冻胀力理论为基础，通过分析地基土冻胀变形规律，运用经典黏弹性力学理论，导出了适用桩基冻胀力三维黏弹性问题的合理表达及解释。

（2）提出求解桩基冻胀力三维黏弹性方程的方法及思路，得到了模型中各参数的表达式及取值。结合已有工程实例进行求解，得到的初始时刻的黏弹性解与已有文献[5]中的弹性解吻合较好。

（3）通过理论计算，首次得到了桩基冻胀力的时空分布三维曲面，可以较直观地反映冻胀力的分布规律。

本论文在理论计算中还存在一定的不足。在计算过程中没有考虑温度变化对土层特性的影响，并且假定冻结强度是常数，所以计算结果与实际值还存在一定的差距，以后的研究中会尝试在该部分做进一步地探讨。

[1]周长庆.黏土切向冻胀力的试验研究[J].低温建筑技术,1979,(1):5－14.ZHOU Chang-qing.The experimental research of tangential frost force in clay[J].Low Temperature Architecture Technology,1979,(1):5－14.

[2]丁靖康.切向冻胀力的野外试验研究[C]//第二届全国冻土学术会议论文选集.兰州:甘肃人民出版社,1983:251－256.

[3]截惠民,田德廷,隋咸志.钢筋混凝土桥桩切向冻胀力研究[C]//第三届全国冻土学术会议论文选集.北京:科学出版社,1989:141－149.

[4]周有才.按基础约束范围内冻胀变形计算冻胀力[J].冰川冻土,1985,7(4):335－346.ZHOU You-cai.According to the frost heave within the scope of foundation constraints to calculate the frost heave force[J].Journal of Glaciology and Geocryology,1985,7(4):335－346.

[5]赖远明,朱元林,吴紫汪.桩基冻胀力三维问题的积分方程解法[J].铁道学报,1998,20(6):93－97.LAI Yuan-ming,ZHU Yu-lin,WU Zi-wang.A simple integral equation method for three-dimensional frost heaving force problem of piles[J].Journal of the China Railway Society,1998,20(6):93－97.

[6]李洪升,刘增利,杨海天.地基土冻胀位移分析及计算模式[J].冰川冻土,1995,17(增刊):89－95.LI Hong-sheng,LIU Zeng-li,YANG Hai-tian.A calculation model and analysis of frost heave deformation for foundation soil[J].Journal of Glaciology and Geocryology,1995,17(Supp.):89－95.

[7]徐学燕,李海山,邱明国,等.桩基础约束条件下季节冻土场地冻胀量的二维数值求解[J].哈尔滨建筑大学学报,2001,34(6):8－11.XU Xue-yan,LI Hai-shan,QIU Ming-guo,et al.Calculation of frost heave in seasonal frozen soil under piled foundation restrain condition[J].Journal of Harbin University of Civil Engineering and Architecture,2001,34(6):8－11.

[8]MINDLIN R.Force at a point in the interior of a semi-infinite solid[J].Physics,1936,7(5):195－202.

[9]童长江,管枫年.土的冻胀与建筑物冻害防治[M].北京:水利电力出版社,1985:69－81.

[10]徐学祖,王家澄,张立新,等.土体冻胀和盐胀机制[M].北京:科学出版社,1995:1－118.

[11]刘鸿绪,朱广祥,尹东岭,等.地基土冻胀的宏观分析[J].冰川冻土,2003,25(3):347－350.LIU Hong-xu,ZHU Guang-xiang,YIN Dong-ling,et al.Macrograph analysis about subsoil frost heaving[J].Journal of Glaciology and Geocryology,2003,25(3):347－350.

[12]祝彦知,仲政.竖向力作用在黏弹性土体内部时的解答与应用[J].应用力学学报,2006,23(4):547－555.ZHU Yan-zhi,ZHONG Zheng.Viscoelastic solutions with applications semi-infinite soil subjected to vertical force[J].Chinese Journal of Applied Mechanics,2006,23(4):547－555.

[13]祝彦知,仲政.黏弹性半空间体内部作用水平力时的理论分析[J].应用力学学报,2007,24(4):544－549.ZHU Yan-zhi,ZHONG Zheng.Semi-infinite viscoelastic solid subjected to horizontal load[J].Chinese Journal of Applied Mechanics,2007,24(4):544－549.

[14]李洪升.冻土与基础间的相互作用[C]//全国首届结构与介质作用学术会议论文集.南京:河海大学出版社,1993:362－366.

[15]孙洪伟,王德君,曲祖光,等.季节性冻土地区人工湖岸船台桩基础“冻拔”现象的观测[J].长春工程学院学报(自然科学版),2007,8(4):1－4.SUN Hong-wei,WANG De-jun,QU Zu-guang,et al.The observation of upward freezing pulling phenomenon about pile foundation applied to the artificial lakeshore shipway of garden buildings in seasonal frozen soil zone[J].Journal of Changchun Institute of Technology(Natural Science Edition),2007,8(4):1－4.