转台系统抗扰动容错控制

关 威，高瀚斐，梁 鹏

(沈阳航空航天大学 自动化学院，沈阳 110136)

转台系统抗扰动容错控制

关 威，高瀚斐，梁 鹏

(沈阳航空航天大学 自动化学院，沈阳 110136)

在实际工作中，直接驱动数控转台因为缺少了中间传动环节的扰动缓冲作用，系统稳定性大大降低。扰动成为影响转台正常工作的关键因素，采用自适应律在线调节自适应率参数的方法，通过设计一个自适应抗扰动容错反馈控制器，从而保证转台系统在出现故障的情况下依然具有较高的扰动容许能力。采用线性矩阵不等式技术，仿真比较自适应控制算法与系统固定增益算法，结果表明自适应容错控制器使系统更加稳定。

容错控制；自适应性能；线性矩阵不等式

随着高新技术流向传统产业，机电一体化产品得到前所未有的发展，直接驱动伺服电机技术凭借其超高速和超精度的特点成为伺服系统的主导执行电机[1-2]。目前绝大多数的数控机床仍然是采用传统驱动方式，其中极少数电机产品采用直接驱动数控转台，这类产品在直接驱动多轴联动高档数控机床中的应用更为少见，原因是直接驱动转台系统存在一定的弊端，主要因为驱动部件和执行部件合二为一，缺少了中间传动环节的缓冲作用，外界及自身的任何扰动无缓冲地作用在电机上，这就对系统的抗干扰能力和稳定性提出更高的要求。然而，环形永磁力矩电机的设计仅仅是为进一步提高系统性能开辟了道路，要保证直接驱动转台系统在故障模式下依然具有很好的抗扰动能力的关键是所设计的控制器[3-5]。

1 构建数学模型

环形永磁力矩电机[6]在静止时也能提供很高的电磁转矩,如图1所示。

图1 环形永磁力矩电机直接驱动转台

当只考虑基波分量时，转台系统在d-q坐标系下的动态方程表示为：

(1)

说明：Rs是定子相绕组电阻，ω是转子的电角速度，ψ是机械角速度，J是转台系统的转动惯量，B是为粘滞摩擦系数，Ψf是永磁磁链，Te是电磁转矩，TL是负载转矩，p是极对数。KT=3pΨf/2为环形力矩电机的转矩系数。

2 反馈控制器的设计

2.1 问题描述

转台系统的动态方程转化为一般的系统状态方程[7]：

(2)

其中，x(t)系统状态，σ(u)∈Rm是带有饱和现象的输入，w(t)是扰动L2[0,∞]输入。描述带有故障率ρ的故障模型：

uF(t)=(I-ρ)σ(u(t))

(3)

2.2 结构设计

转台系统转化成带有执行器故障和执行器饱和现象的系统[8]

(4)

控制器结构如下：

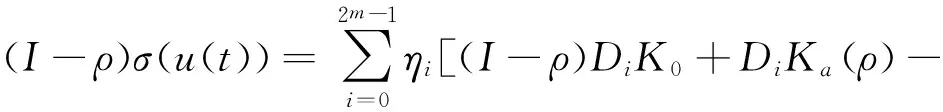
(6)

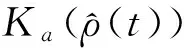
η∈Λ,ηi=[η0,η1,…,η2m-1]

(7)

(9)

P=δX-1,K0=Y0X-1,Kaj=YajX-1,Kbj=YbjX-1,

Haj=ΦajX-1,Hbj=ΦbjX-1,lj>0(j∈I[1,m])

控制器的增益结构描述如下

(10)

根据自适应律(8)在线选择K0=Y0X-1,Kaj=YajX-1,Kbj=YbjX-1。

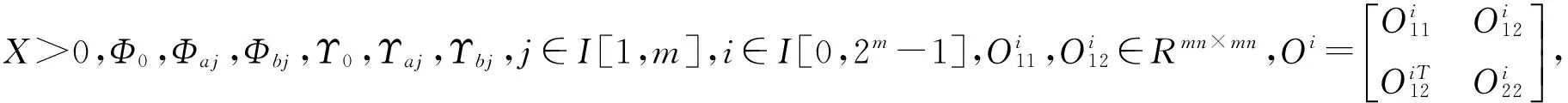
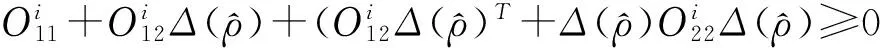
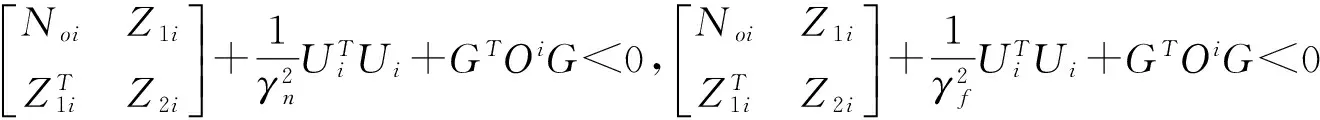
(11)

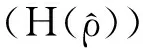
(12)

3 算法与仿真

(a)求解最优化问题：

minη=αηn+βηf+γηδs.t.(a)(11)b

最优解得ηn,ηf,ηδ,X,Y0,YajYbj,Φ0,Φaj,Φbj,j∈[1,m]。

(b)通过(10)确定控制器的相关参数K0,Kaj,Kbjj∈[1,m]。

(c)确定系统的自适应律(9)式。

表1 环形永磁力矩机参数[14-15]

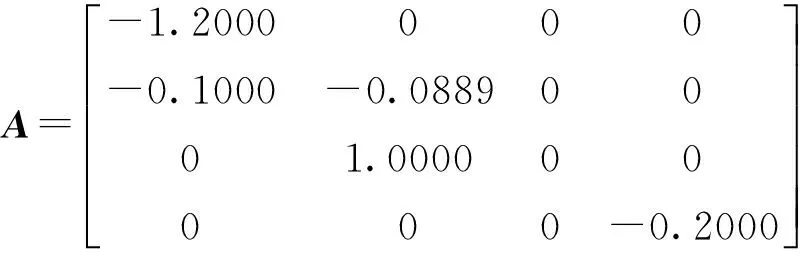
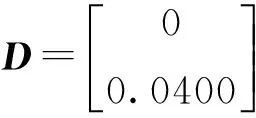
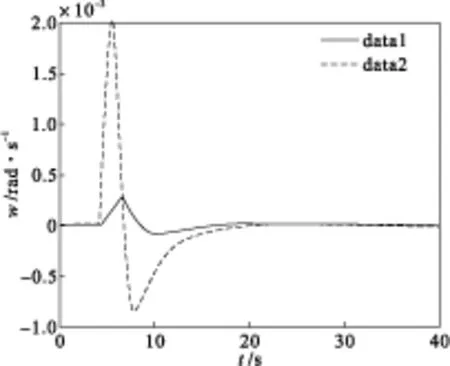
注：实线是自适应控制器，虚线是固定增益控制器 图2 故障模式下的x(2)状态响应曲线

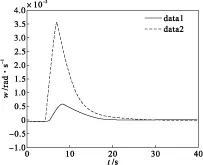
注：实线是自适应控制器，虚线是固定增益控制器 图3 故障模式下的x(3)状态响应曲线

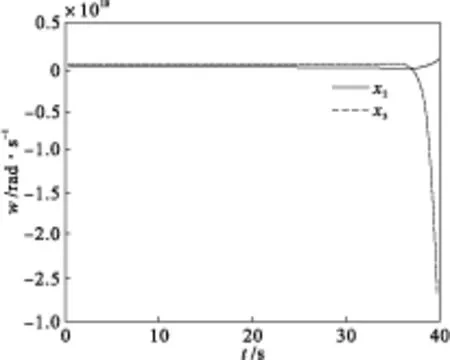
状态响应曲线(虚线为x(2)，实线为x(3)) 图4 故障下固定增益控制器作台系统

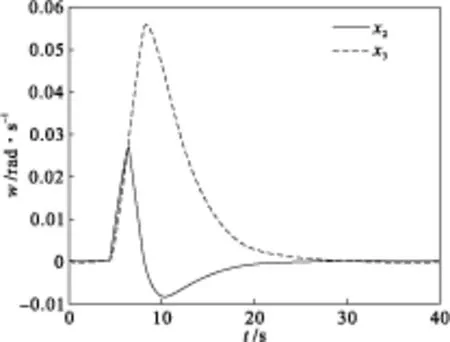
状态响应曲线(虚线为x(2)，实线为x(3)) 图5 故障模式下自适应控制转台系统

4 结论

转台系统在故障模式下状态曲线如图2和图3所示，可见自适应具有更好的鲁棒稳定性。转台系统在故障模式下，扰动状态响应曲线如图4和图5所示，固定增益控制器的状态响应曲线，在扰动过大的情况下，系统状态响应曲线已经发散，同样的扰动下，自适应控制器系统状态响应曲线(图5)依然是渐进稳定的。由此说明，自适应控制方法在转台系统的应用比固定增益控制方法有更好的效果。从而保证了直接驱动转台系统在故障模式下依然具有很好的抗扰动能力，为直接驱动伺服电机技术在伺服系统的广泛应用提供了有力保障。

[1]孙宜标，杨雪，夏加宽.采用鲁棒微分器的永磁直线同步电机二阶滑模控制[J].中国电机工程学报.2007，27(33)：6-10.

[2]范岩.多电机同步控制策略的改进[J].机电工程，2007，24(6):65-66.

[3]王道涵,王秀和,丁婷婷,等.基于磁极不对称角度优化的内置式永磁无刷直流电动机齿槽转矩削弱方法[J].中国电机工程学报，2008,28(9):66-70.

[4]卢晓慧,梁加红.直驱型机电作动器中永磁容错电机非线性模型研究[J].中国电机工程学报,2012,32(18):145-151.

[5]刘治钢,王军政,赵江波等.永磁同步电机神经网络自适应滑模控制器设计[J].电机与控制学报,2009,13(2):290-295.

[6]宋春华,胡丹,柯坚.内模控制在 PMSM 矢量控制中的应用[J].电力电子技术,2007 (9):36-38.

[7]胡寿松，王执铨，胡维礼.最优控制理论与系统[M].北京：科学出版社，2005：3-16.

[8]徐巧林.无人机鲁棒性及自适应容错控制技术研究[D].南京:南京理工大学,2012:34-38.

[9]吕刚,范瑜,李国国,等.永磁直线电机运输系统中的模糊增益神经控制[J].北京交通大学学报,2008(05):81-88.

[10]郭健，陈庆伟，吴益飞，等.一类非线性不确定系统的自适应鲁棒控制[J].控制理论与应用,2010，27(8)：1081-1092.

[11]赵希梅，郭庆鼎.数控机床多轴联动伺服电机的零相位自适应鲁棒交叉耦合控制[J].中国电机工程学报,2008，28(12)：129-133.

[12]刘毅男，曹立佳，张超.一类不确定非线性系统基于SVR的Backstepping自适应跟踪控制[J].东南大学学报,2012，9(24)：20-24.

[13]刘火龙.基于LMI技术的被动容错控制系统设计方法研究[D].沈阳:东北大学,2010:45-60.

[14]范岩.多电机同步控制策略的改进[J].机电工程，2007，24(6):65-66.

[15]盛义发,喻寿益,洪镇南.一种新颖的永磁同步电机直接转矩控制方法[C].第二十七届中国控制会议论文集,2008.

(责任编辑：刘划 英文审校：刘敬钰)

Fault-tolerant control of turntable system against disturbances

GUAN Wei,GAO Han-fei,LIANG Peng

(College of Automation,Shenyang Aerospace University,Shenyang 110136,China)

In practice,there is no buffer disturbance of intermediate transmission links in the direct driven NC rotary table,greatly lowering stability of the system.Solving perturbation problem is the key to ensure the turntable to work properly.The adaptive law regulating adaptive rate parameters online is used to design an adaptive fault-tolerant controller,ensuring a high disturbance allowable capacity of the turntable system in case of failure.The linear matrix inequality technique is adopted to make artificial comparison between adaptive control algorithms and fixed gain algorithms,which shows that the adaptive fault-tolerant controller makes the system more stable.

Fault-tolerant control;Adaptive performance;the linear matrix inequality

2015-01-16

国家自然科学基金青年基金(项目编号：61203087)；辽宁省优秀人才培养计划第二层次(项目编号：LJQ2013017)；沈阳航空航天大学博士启动项目(项目编号：11YB18)

关威(1980-)，男，辽宁沈阳人，副教授，主要研究方向：受限系统、容错控制、非线性系统，E-mail：guanweihaha@163.com。

2095-1248(2015)03-0063-04

TM921.543

A

10.3969/j.issn.2095-1248.2015.03.012