热声载荷作用下薄壁壳结构非线性 响应及疲劳寿命估算

张国治，沙云东，朱 林，冯飞飞

(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136)

热声载荷作用下薄壁壳结构非线性 响应及疲劳寿命估算

张国治，沙云东，朱 林，冯飞飞

(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136)

高超飞行器表面薄壁结构在热声载荷下发生复杂非线性响应，结构内部快速变化的应力对结构疲劳寿命有显著影响。在原有平板结构计算结果基础上，利用有限元法对薄壳结构在热声载荷下的大挠度非线性随机响应进行了分析，得到了薄壁壳在均匀温度下的非线性响应，结合线性损伤理论和雨流循环计算法对薄壁壳结构疲劳寿命进行了估算。结果表明，薄壁壳在热声载荷下的非线性响应呈现明显的稳定-失稳-稳定过程，结构寿命在失稳状态下受到严重影响；非线性响应的应力幅值和均值共同表征结构的疲劳损伤特性。

薄壁壳；热声载荷；热屈曲；跳变响应；疲劳寿命

高超飞行器在飞行过程中面临着极其严峻复杂的载荷环境，包括机械载荷、气流脉动、航空动力加热以及高强度噪声载荷等。近些年来，热载荷与声载荷成为飞行器壁板设计的重要考虑因素。飞行过程中由于喷气冲击或者压力脉动的作用，产生的噪声声压级最高可达180 dB。而由气动力产生的热量，导致温度最高可达3 000°F[1]。在热噪声载荷作用下，高超飞行器壁板结构会呈现出非线性响应特征，产生复杂的应力应变状态。薄壁结构在这种复杂应力应变状态下,其疲劳寿命会显著降低，对飞行器的可靠性设计造成严重威胁。因此，研究航空薄壁结构非线性响应与疲劳寿命估算具有重要意义。

90年代后，随着先进技术的发展，有限元法广泛应用于分析计算结构在复杂载荷作用下的响应。国外Chen和Mei[2-3]采用FEM对梁和矩形板在热声载荷作用下的动态响应进行了计算；Dhainant[4]等采用FEM缩减模态法计算了各向同性板和复合材料板在热声载荷作用下的非线性响应。国内沙云东教授[5-8]等采用FEM/Galerkin法对热声激励下的金属板、复合材料等薄壁板结构的非线性响应进行了计算，同时采用改进雨流计数法与累计损伤理论相结合的方法对金属薄壁结构的疲劳寿命进行估算与分析。

由于飞行器结构多为带有曲率的薄壁壳结构，因此，对薄壁壳结构在热声载荷作用下的非线性响应与疲劳寿命计算与分析更贴近于实际情况。本文在前人研究的基础上，以四边简支铝合金薄壁壳作为研究对象，采用有限元法对薄壁壳在热声载荷作用下的非线性应力响应进行了计算与分析，并结合Palmgren-Miner线性损伤理论和改进的雨流循环计算法[9]对薄壁壳结构的疲劳寿命进行了估算。

1 热应力薄壁壳有限元基本方程：

位移与应变之间关系：

ε=ε0+z0{κ}

(1)

根据冯·卡门大挠度板壳理论，可得圆柱壳的膜应变和曲率[10]为：

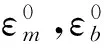
(2)

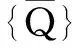
δW=δWint-δWext=0

(3)

其中，δWint和δWext分别为内力和外力的虚功[11]。整理单元矩阵和采用适当的边界条件，推导出运动方程：

(4)

其中，M为质量矩阵，K为线性刚度矩阵，w为法向位移向量，P为法向压力向量。K1和K2为非线性刚度矩阵。KΔT为带有热应力的刚度矩阵，{PΔT}为由于热应力产生的法向应力向量。对公式(4)进行泰勒级数展开并用牛顿迭代法[12-14]进行求解，结合边界条件可求得结构的位移响应。通过公式(5)中的应力应变关系，转换得到薄壁壳的应力响应。

(5)

2 应用实例

本文利用有限元数值计算方法对薄壁壳在热声载荷作用下的响应进行了计算，并重点对薄壁壳在定常声压级、不同温度下的应力响应进行了分析。最后利用改进的雨流计数与Miner线性累积理论相结合的方法针对薄壁壳在热声激励下的疲劳寿命进行了预测。采用铝合金薄壁壳作为研究对象，边界条件为四边简支，具体材料参数如表1所示。其中，a，b和h分别为薄壁壳的长、板壳弧长和厚度。

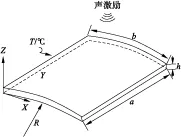
图1 薄壁板壳

表1 铝合金薄壁板壳几何参数及属性

所要研究的载荷主要分为热载荷与声载荷两种。热载荷主要考虑为均匀分布在薄壁壳上的稳态热载荷，声载荷主要选用有限带宽高斯白噪声，其频率范围为0-1 500 Hz,载荷时长为1 s。功率谱密度函数如下所示

(6)

其中，G(f)为有限带宽高斯白噪声功率谱密度，SPL为总声压级，Δf为频带宽度，取0～1 500 Hz。为了能够形象地对声载荷进行表述，以总声压级为170 dB为例，声载荷时间历程及相应的功率谱密度如图2和图3所示。

薄壁壳结构受到热载荷作用，由于约束作用而不能自由伸展或膨胀，导致结构内部产生热应力，从而致使结构出现热屈曲现象。假设薄壁壳均匀受热，结构前6阶临界屈曲温度计算结果如表2所示。计算薄壁壳在热声载荷作用下振动响应之前，首先对薄壁壳进行结构模态分析，确定设计结构或者部件的振动特性，即薄壁壳的模态频率如表3所示。为便于表述，将临界热屈曲系数S作为加载温度和第一阶临界热屈曲温度的比值。当S>1时，薄壁壳发生热屈曲现象。

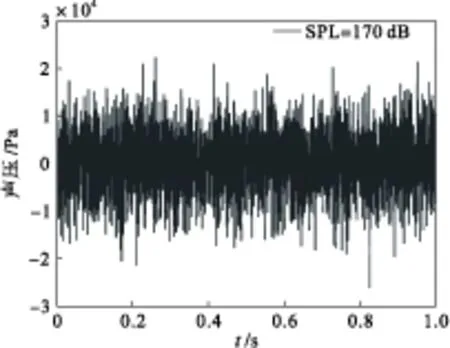
图2 有限带宽高斯白噪声(SPL=170 dB)

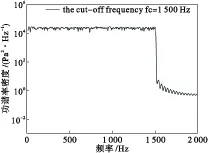
图3 有限带宽高斯白噪声功率谱密度(SPL=170 dB)

表2 四边简支铝合金薄壁壳的临界屈曲温度

表3 四边简支铝合金薄壁壳的模态频率温度

2.1 薄壁壳的热声响应计算与分析

本文主要针对薄壁壳在定常声压级170 dB、不同热屈曲系数S下的应力响应进行计算，结果如图4所示。由图4(a)、图4(b)与图4(c)可以发现，热屈曲前，随着温度的增加，薄壁壳中心位置的应力幅值不断增加。在发生热屈曲前，虽然热应力随着温度也在增加，但由于发生热屈曲时，出现软化现象，在声压级较大的情况下弯曲拉伸应力与压缩热应力的叠加数值大于弯曲压缩应力，因而应力响应在热屈曲时主要表现为拉伸应力，即应力均值为正值。由图4(d)和4(e)可知，当热屈曲系数达到1.2与1.4时，薄壁壳在热后屈曲阶段软化效果最为明显，薄壁壳此时在热声载荷作用下表现为持续跳变和间歇跳变，这时应力的幅值最大。由于薄壁壳发生热屈曲，主要出现两个平衡位置，即与薄壁壳初始弯曲方向相同的主热屈曲平衡位置，以及背向弯曲方向的第二热屈曲平衡位置。由于薄壁壳初始弯曲方向所致，在发生跳变时，围绕主热屈曲平衡位置振动的频率明显高于第二热屈曲平衡位置。由图4(f)可知，当S=1.2时，薄壁壳不再出现软化现象，反而开始硬化，应力幅值明显减小，且由于初始弯曲方向的优势，主要围绕主热屈曲平衡位置振动。图4(d)、4(e)和4(f)显示，薄壁壳在热后屈曲阶段主要表现为拉伸状态，即随着温度的增加，应力的均值逐渐增大。

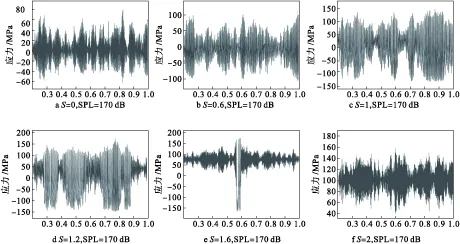
图4 不同热屈曲系数(S)下薄壁板壳中心位置处应力响应时间历程(SPL=170 dB)

结合信号处理手段，通过应力时间历程自相关函数的傅里叶变换，对应力响应的功率谱进行分析。图5给出了在定常声压级170 dB、不同S下(即不同温度取值)薄壁壳屈曲前和屈曲后的功率谱密度。对比发现：屈曲前，随着温度增加，薄壁壳基频减小，即刚度降低，结构进入软化状态；屈曲后，随着温度增加，薄壁壳基频增大即刚度增加，结构进入硬化状态。由图5(b)可知，在薄壁壳发生跳变现象时，基频的频带明显变宽，软化现象最为明显。

2.2 累计损伤理论

本文在基本的应力寿命关系基础上，给出了考虑平均应力影响的寿命估算模型[15]：

(7)

其中，ΔSeff为平均Von Mises应力，σf=1 602 MPa，b=0.154。本文采用Morrow TFS平均应力公式：

(8)

其中，Sa为应力循环幅值；Sm为应力循环均值，STFS=610 MPa。工程上广泛应用的累计损伤理论是Miner理论，即在循环载荷作用下，可以线性地累加疲劳损伤，各个应力水平相互独立，互不相关，直到损伤累加到一定数值时，结构部件发生结构疲劳破坏。在确定性载荷作用下的线性疲劳损伤可以表示为：

图5 不同屈曲系数(S)下薄壁壳应力响应功率谱密度(SPL=170 dB)

(9)

其中，Ni为在第i级等幅值应力载荷下的工作循环次数；(Nf)i为第i级等幅值应力载荷下结构发生破坏时的循环次数。本文通过雨流循环计数获得应力循环的联合概率密度函数的数值统计。假设第k次雨流循环(RFC)的局部极大值与极小值分别为Smax和Smin，时间为Tr内的总损伤为：

(10)

其中，P(Smin,Smax)为应力循环极小值和极大值的联合概率密度函数；Nf(Smin,Smax)为应力循环作用下的疲劳寿命，取决于平均应力模型的选择。采用有限时长信号的雨流循环矩阵(RFM)估算P(Smin,Smax)：

(11)

(12)

其中，RFD(Smin,Smax)为二维雨流循环损伤矩阵。当E[D]=1，结构发生疲劳失效。疲劳寿命时间为：

(13)

2.3 疲劳寿命估算

典型的雨流循环矩阵(RFM)如图6和图7所示。在RFM中，X轴和Y轴分别为循环对(mk,Mk)的极小值和极大值，循环计数结果对应RFM中一点。将RFM离散为n×n块后，第(i,j)块对应Z轴的循环对数目即RFM(Si,Sj)的数值。由于循环对中极小值必然小于极大值，所以循环只分布在平面图的左上区域。循环对R=1与对角线距离越远，循环的幅值越大；循环对与R=-1对角线的距离越远，循环的平均应力越大。

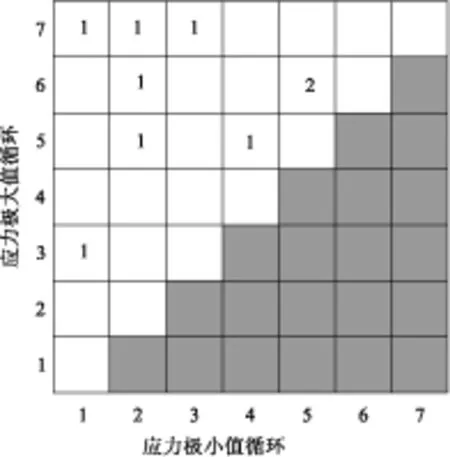
图6 雨流循环矩阵

基于前面得到的薄壁板典型节点的动态响应分析，进一步进行随机声疲劳损伤估算和分析。利用时域数值模拟出的动态响应数据，采用雨流计数法估算热声疲劳寿命。当SPL=170 dB时，四边简支薄壁壳在不同屈曲系数S下的应力雨流循环矩阵(RFM)和雨流循环损伤矩阵(RFD)如图8～图15所示。当S=0时，薄壁壳围绕初始平衡位置振动，应力循环均值近似为零，如图8所示；当S=1时，应力响应水平提高，应力循环均值增大，临界屈曲时的应力循环幅值明显增加，循环块整体左上移动同时循环块扩散，如图10所示；屈曲后结构频繁跳变时，应力循环幅值增大，均值增大，如图12所示；当温度足够高时，结构停止跳变运动，围绕一个屈曲后平衡位置振动，温度越高，应力循环的幅值越小，均值越大，如图14所示。声压级为170 dB、不同温度下薄壁壳疲劳寿命估算的结果如表4所示。

图7 雨流循环矩阵示意图

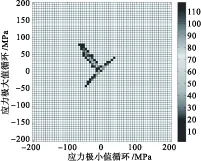
图8 雨流循环矩阵(0,170)

图9 雨流损伤矩阵(0，170)

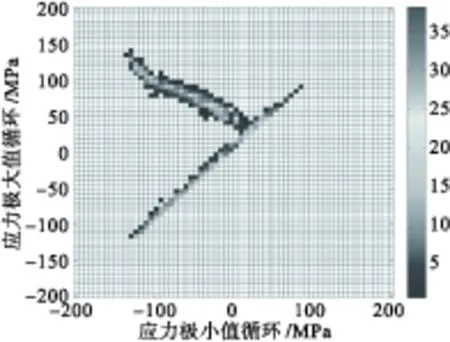
图10 雨流循环矩阵(1,170)

图11 雨流损伤矩阵(1，170)

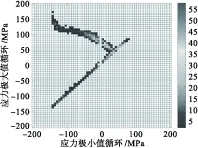
图12 雨流循环矩阵(1.2,170)

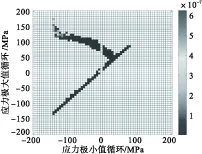
图13 雨流损伤矩阵(1.2，170)

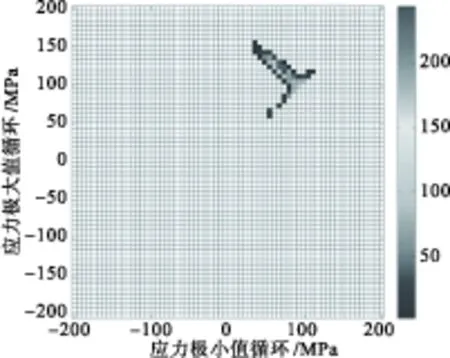
图14 雨流循环矩阵(2,170)

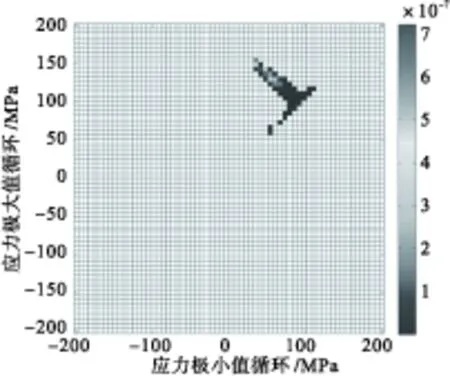
图15 雨流损伤矩阵(2，170)

表4 不同热屈曲系数(S)下薄壁壳疲劳寿命估算(SPL=170 dB)

3 结论

对薄壁壳在热声载荷下的仿真计算结果表明：

(1)声压级为170dB时，结构发生屈曲前，随着温度的升高，薄壁壳的模态基频降低；屈曲后，随着温度升高，薄壁壳模态基频升高。结构跳变说明薄壁壳在热声载荷作用下，结构刚度发生了变化，屈曲前后呈现稳定-失稳-稳定的过程。

(2)屈曲后，薄壁壳发生跳变时，幅值增大，薄壁壳主要围绕主平衡位置振动。通过损伤矩阵发现结构疲劳损伤同时受振动响应的均值和幅值的影响：结构发生屈曲前，随着温度升高，结构幅值和均值都增大；屈曲后，幅值先增大后减小，均值持续增大。两者相比较，振动响应均值更能表征结构疲劳损伤特性。

(3)在热声载荷作用下，薄壁壳非线性响应对结构寿命有显著影响。频繁的跳变响应使结构疲劳寿命降低，且随着温度升高，结构寿命曲线呈现先降低后升高的特性。

[1]Blevins R D,Holehouse I,Wentz K R.Thermoacoustic loads and fatigue of hypersonic vehicle skin panels[J].Journal of Aircraft,1993,30(6):971-978.

[2]Chen R X,Mei C.Finite element nonlinear random response of beams to acoustic and thermal loads applied simultaneously[C].The Proceedings of 34th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics and Materials Conference,1993.

[3]Charles C Grsy,Chuh Mei.Finite element analysis of thermal post-bucking and vibrations of thermally buckled composite[J].Journal of Sound and Vibration,2008(30):188-190.

[4]Dhainaut J M,Guo X Y,Mei C,et al.Nonlinear random response of panels in an elevated thermal-acoustic environment[J].Journal of Aircraft,2003,40(4)：683-691.

[5]Yundong Sha,Jiyong Li,Zhijun Gao.Dynamic response of pre/post buckled thin-walled structure under thermo-acoustic loading[J].Applied Mechanics and Materials 80(2011):536-541.

[6]Yundong Sha,Zhijun Gao,Fei Xu,et al.Influence of thermal loading on the dynamic response of thin-walled structure under thermo-acoustic loading[J].Applied Mechanics and Materials,2011(2-3)：876-881.

[7]沙云东，魏静，高志军，等.热声载荷作用下薄壁结构的非线性响应特性[J].航空学报，2013,34(6):1336-1346.

[8]沙云东，魏静，高志军，等.热声激励下金属薄壁结构的随机疲劳寿命估算[J].振动与冲击，2013,34(10):162-166.

[9]Bishop NWM and Sherratt F.A theoretical solution for the estimation of “rainflow” ranges from power spectral density data[J].Fatigue & Fracture of Engineering Materials & Structures,1990,13(4):311-326.

[10]Xinyun Guo,Adam Przekop,Chuh Mei.Nonlinear Flutter of Cylindrical Panels Under Yawed Supersonic Flow Using Finite Elements Mohamed Azzouz,Structural Dynamics & Materials Conference,April,2004:19-22.

[11]Gray C C,Mei C.Finite element analysis of thermal post-buckling and vibrations of thermally buckled composite plates[D].Old Dominion University,1991.

[12]Yundong Sha,Fei Xu,Zhijun Gao.Nonlinear response of carbon-carbon composite panels subjected to thermal-acoustic loadings[J].Applied Mechanics and Materials,2012,117:876-881.

[13]Mei C,Locke J.A finite element formulation for large deflection random response of thermally bucked plates[J].AIAA paper,1989:89-1354.

[14]Dhainaut J M.Nonlinear response and fatigue estimation of surface panels to white and non-white gaussian random excitation[D].Ph D Dissertation,Old Dominion University,Norfolk:VA,2001.

[15]Carpinteri A,Spagnoli A,Vantadori S.A multiaxial fatigue criterion for random loading[J].Fatigue & Fracture of Engineering Materials & Structures,2003,26(6):515-522.

(责任编辑：宋丽萍 英文审校：刘敬钰)

Nonlinear response and fatigue life estimation of thin-shell structures under thermo-acoustic loads

ZHANG Guo-zhi，SHA Yun-dong,ZHU Lin，FENG Fei-fei

(Liaoning Province Key Laboratory of Advanced Measurement And Test Technology of Aviation Propulsion Systems, Shenyang Aerospace University,Shenyang 110136,China)

Thin structures on the surface of hypersonic aircrafts subject to thermal-acoustic loadings will exhibit complex nonlinear response,and the fatigue life has been influenced by rapid changing stress of the inner structure.Based on the results of the original thin-panels,a finite element method was used to analyze the nonlinear random response and large deflection of thin-shells under thermo-acoustic loadings.The nonlinear response of thin-shells was obtained under the even temperature,and the fatigue life was estimated by the rain flow cycle counting method and Miner accumulative damage model.Results show that the nonlinear response of thin-shells under thermo-acoustic excitation was a significant stable-unstable-stable process,and the structure life was much affected within the unstable state.Structure fatigue damage characteristics were indicated by both stress amplitude and mean value of the nonlinear response.

thin-shell;thermo-acoustic excitation;thermal-buckling;snap-through;fatigue life

2013-10-09

张国治(1986-)，男，吉林柳河人，硕士研究生，主要研究方向：航空发动机强度、震动及噪声,E-mail:zhangguozhi617@163.com；沙云东(1966-)，男，黑龙江阿城人，教授，主要研究方向：航空发动机强度、震动及噪声,E-mail:Ydsha2003@vip.sina.com。

2095-1248(2015)03-0018-07

V214.4

A

10.3969/j.issn.2095-1248.2015.03.004