亚声速自由射流装置喷管-进气道位置关系

亚声速自由射流装置喷管-进气道位置关系

王键灵1a，徐让书1a,1b，康 建2，张钊瑞1a1.沈阳航空航天大学a.航空航天工程学部(院)；b.辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136； 2.济南柴油机股份有限公司 销售部，济南 250000)

为了预测航空发动机高空模拟自由射流试验中飞机进气道-发动机组合体前方的亚声速流场特性，优化试验舱的气动设计，采用CFD方法在亚声速自由射流和真实大气飞行条件下对某战斗机进气道的外流场进行数值模拟。结果发现进气道距离喷管出口太近会使流场相似度下降，飞行马赫数、攻角和发动机进气流量都会对进气道的最佳安置距离产生影响。

自由射流；发动机高空模拟；进气道；位置关系；数值模拟

高空台是国家战略性资源，高空模拟是自主研制先进航空发动机必不可少的重要手段和工具，一个国家的高空模拟能力和技术水平已成为该国自主研制先进航空发动机能力和水平的一个重要标志[1]。自由射流式高空舱可以模拟包括进气道在内的整个动力装置的内部流动条件，还能模拟沿某一轨迹的飞行条件。美国ASTF的设计工作早在1973年就开始了，在1993年C2舱已经投入使用。国内的自由射流高空台也正在建设当中[2-8]。

自由射流气流通过喷管加速到飞行马赫数，在喷管出口形成自由射流核心区。在核心区内可以认为流体速度不变，亚声速自由射流高空台试验正是用自由射流核心区来模拟大气飞行环境。在亚声速条件下进气道的安放位置的选取很关键。如果距离喷管出口太近会造成喷管阻塞，使核心区流场发生改变无法与真实大气环境相似；距离太远会使试验件置于核心区外，使流场达不到试验要求。本文研究了进气道安置距离过近对喷管出口马赫数的影响，模拟了不同攻角时真实大气飞行环境和自由射流环境下进气道附近的流场情况。通过比较自由射流环境中进气道进口总压分布与真实大气环境的相似程度，确定了不同攻角和飞行马赫数条件下试验件安放的最佳距离。

1 控制方程与计算模型

1.1 控制方程

质量守恒定律、动量守恒定律和能量守恒定律是流体力学中最基本的三大定律。控制方程为N-S 方程,它全面考虑了流体的粘性、热传导和可压缩性等方面的影响，是以连续介质流体流动的质量、动量和能量守恒定律为基础建立起来的。

质量方程为：

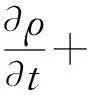
(1)

式中,▽为哈密顿算子。

动量方程为：

(2)

能量方程为：

(3)

其中，δw为运输功，δwf为摩擦损耗[9-12]。

1.2 计算模型及边界条件

计算了多种工况下真实大气环境和自由射流环境中进气道附近的流场，并以真实大气环境下的流场作为标准，与自由射流环境的流场进行对比。真实大气模型是将进气道置于直径30 m，长30 m的圆柱体中，圆筒壁面均采用压力远场边界条件。高空台模型的计算域如图1所示，试验舱主要由亚声速喷管、转动装置和舱体三部分组成。试验舱主体部分是直径8.5 m，长15 m的圆柱体，转动装置为直径5 m的半球体。喷管进口为压力进口边界条件，试验舱出口为压力出口边界条件，其它壁面均为无滑移壁面边界条件。自由射流气体经过一个二元亚声速喷管加速到飞行马赫数。喷管由长3 m的渐缩段和2 m的直段组成，进出口面积比为2∶1，出口截面为长1.6 m，宽1.2 m的矩形。喷管和转动装置刚性连接，改变飞行攻角时，喷管和转动装置以舱体左端面的中心点为圆心转动。进气道模型采用美国某战斗机的腹下式S型进气道，进口截面积为0.653 m2，进气道部分长5.45 m，发动机及尾喷管部分长3.96 m。发动机部分不作为计算域，在发动机进口和出口截面处各用一个质量流量进口(发动机进口截面的质量流量进口作为质量流量出口使用)，以便模拟控制发动机进气流量。为了简化模型，计算域内所有壁面都看做薄壁结构。

图1 计算域模型

2 网格划分

计算网格采用ANSYS-ICEM进行划分。在计算粘性流体时，结构网格较非结构网格更具有优势，考虑本次模拟的流体为粘性流体，故均使用结构网格划分。大气环境和自由射流环境的计算域模型差别较大，网格划分情况有较大差异，但各个模型的网格数量均在250万到320万之间。在Determinant 2×2×2方法下检查网格质量均在0.55以上。在自由射流模型的网格划分时，试验舱远离进气道的部分网格比较稀疏，喷管出口以及进气道附近网格进行加密[13-16]。近壁处理采用标准壁面函数，考虑到计算域较大，舱体壁面不作为关注区域，所以仅控制喷管壁面和进气道壁面y+符合要求即可。高空舱整体网格划分情况如图2所示，喷管与进气道区域的网格划分情况如图3所示。

图2 计算域网格

图3 进气道前区域网格

3 计算方法

采用ANSYS-FLUENT15.0作为计算软件，使用稳态求解器进行求解。因为Realizablek-ε模型能够更精确地模拟平面和圆形射流的扩散速度，同时在旋转流计算、带方向压强梯度的边界层计算和分离流计算等问题中，计算结果更符合真实情况，故采用Realizablek-ε湍流模型。本文所有工况的飞行马赫数中最小为0.4，气体的压缩性不可忽略，所以采用基于密度的求解器。气体的密度、比热等参数以多项式拟合的形式给出。由于需要计算的工况很多，因为需要计算的工况很多，出于对时间、计算结果的精度以及经济性的考虑。故使用一阶迎风格式作为离散格式。

4 计算结果分析

4.1 进气道安置距离过近对喷管出口马赫数的影响

亚声速自由射流中进气道与喷管出口的距离是否合理，会直接影响模拟试验的准确性。安置距离太近使喷管被阻塞，喷管出口马赫数达不到模拟要求，无法保证流场的马赫数相似。为了使进气道完全包含于自由射流核心区内，并且考虑到真实试验经济性问题，又必须在保证流场相似的前提下尽量减小安置距离。飞行高度为10 km，飞行马赫数为0.8时，把进气道安置在3个不同位置，喷管对称轴线上的马赫数在喷管出口附近的分布如图4所示。比较3条曲线发现，安置距离只在1.6 m时，喷管出口马赫数达到0.8。安装距离为1.0 m和1.6 m的两条曲线在Y方向位置坐标小于-0.75 m时，能够保证马赫数分布十分接近，都保持随Y方向距离增大而增大的趋势。当Y方向位置坐标大于-0.5 m，安装距离为1.0 m时马赫数不再增加，并且逐渐开始减小，马赫数一直未达到0.8。而安装距离为1.6 m时，马赫数持续增加，在0 m处马赫数达到0.8，然后开始下降。安置距离为0.5 m时，喷管发生严重堵塞，喷管出口马赫数远低于0.8。

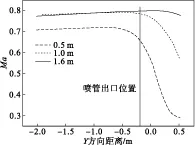
图4 喷管出口附近马赫数

4.2 进气道最佳安置距离的确定

10 km高空，飞行马赫数为0.4、0.6和0.8时，发动机进气流量分别为25.23 kg/s、28.18 kg/s和32.65 kg/s。选取不同的进气道安置距离和不同飞行马赫数，攻角分别为0°，10°和20°时计算自由射流高空台的流场情况，并与其对应工况下的真实大气环境流场比较，确定各个工况下最佳安置距离。

以进气道进口截面作为参考面，由于进气道是对称结构，可在该面的右边半面等间距的建立137个点将其全部覆盖。记录各个点的总压值(自由射流环境每个点总压值记为ptxi，真实大气环境记为ptyi，用下列公式计算出σ：

(4)

当飞行攻角为0°时，不同飞行马赫数进气道进口截面总压分布σ值如图5所示。从σ值分布可以看出，随着进气道安置距离的增加，两种环境下进气道进口总压分布的相似度先减小后增大。马赫数为0.4时，在1.6 m处得到与真实大气环境最为相似的进气道进口总压分布，并且总压分布相似度随安置距离的变化不剧烈。而马赫数为0.6和0.8时，是在1.8 m处得到最为相似的总压分布，并且总压分布相似度随安置距离的变化很剧烈。随着马赫数的增大，进气道最佳安置距离有增加的趋势，并且马赫数越高截面上的总压分布相似程度越低。进气道的存在对上游流场有明显的扰动作用，当安置距离过近时这种扰动更为明显，这使得喷管内的气流产生阻塞，喷管出口流场与真实大气流场产生很大差异，从而导致自由射流环境中的进气道进口截面总压分布与真实大气环境有较大偏差。随着安置距离增加，阻塞作用逐渐减小，进气道进口截面总压分布相似度逐渐升高。这样就可以通过改变进气道安置距离来选取最佳的进气道安置距离。

图5 攻角为0°的进气道进口截面总压σ值

从图5可以看出当马赫数为0.6时，将进气道放置于1.8 m的位置进气道进口总压分布相似程度最好。以此时的工况为例，从总压分布和马赫数分布的角度来比较两种环境下的流场情况。两种环境下的进气道进口位置的总压分布云图如图6所示，马赫数分布如图7所示。从两图中可以看出两种环境下进气道进口附近的总压和马赫数分布情况基本一致。

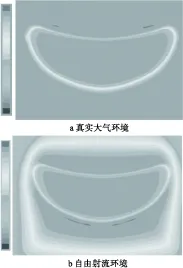
图6 攻角为0°的进气道进口总压分布

图7 攻角为0°的进气道进口马赫数分布

当飞行攻角为10°时，不同飞行马赫数进气道进口截面总压分布σ值如图8所示。从图中可以看出σ值变化趋势与攻角为0°时基本一致，都是随着进气道安置距离的增大而先减小后增加。3种马赫数的最佳安置距离都集中在1.5 m到1.6 m的范围内。随着马赫数的增加，总压分布的相似度降低。

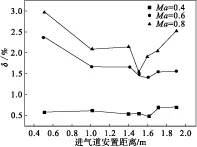
图8 攻角为10°的进气道进口截面总压σ值

当飞行攻角为20°时，不同飞行马赫数进气道进口截面总压分布σ值如图9所示。3种马赫数下进气道进口总压分布σ值均在1.6 m至1.7 m范围内获得较为小的σ值，σ值变化趋势依然保持随安置距离增大而先减小后增大的规律。

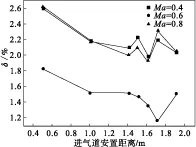
图9 攻角为20°的进气道进口截面总压σ值

通过比较3种攻角的σ值情况，发现攻角在20°以内时，攻角的变化对于进气道安置距离的影响不大。攻角为10°和20°的情况与没有攻角的情况相比较，马赫数为0.6和0.8时有攻角存在使进气道最佳安置距离缩短。

4.4 进气流量对进气道安置距离的影响

当飞行马赫数为0.6和0.8，发动机进气流量不同时，不同安置距离的进气道进口截面σ值分布情况分别如图10和图11所示。同样通过比较σ值的方法来比较进气道进口总压值的相似度。各工况的σ值变化的趋势基本一致，都随着安置距离的增大而先减小后增大。当马赫数为0.6，流量为20 kg/s时，安置距离在1.4 m时就可以得到较为相似的进气道总压分布，而进气流量为28.18 kg/s和36.36 kg/s时，安置距离要在1.8 m时才达到最佳。当马赫数0.8，流量为24.65 kg/s时，安置距离在1.7 m时可以得到较为相似的进气道总压分布，而进气流量为32.65 kg/s和40.36 kg/s时，安置距离也要在1.8 m时才达到最佳。通过比较两种马赫数下，不同发动机进气流量的情况可以看出当发动机流量减小时，最佳安置距离有减小的趋势。

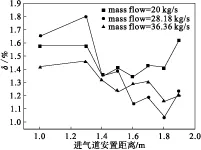
图10 马赫数为0.6时不同发动机进气流量的σ值

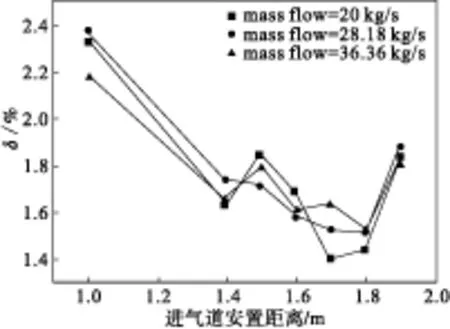
图11 马赫数为0.8时不同发动机进气流量的σ值

5 结论

喷管距离进气道太近会使喷管阻塞，出口马赫数降低，10 km高空飞行马赫数为0.8，安置距离为1.6 m时，喷管出口马赫数达到0.8。

(1)通过比较不同攻角的进气道进口总压分布相似情况，发现进气道安置在1.5 m至1.8 m范围内时能够得到较为相似的进气道进口总压分布；攻角为0°时，飞行马赫数越大，最佳安置距离越大，攻角的存在会使最佳安置距离有减小的趋势。

(2)发动机进气流量对进气道最佳安置距离有影响，随着发动机进气流量减小，进气道最佳安置距离随之减小。

[1]侯敏杰，刘冬根.航空发动机高空台的发展与展望[J].航空科学技术,2012(3):1-4.

[2]杜鹤龄.航空发动机高空模拟[M].北京：国防工业出版社，2002：44-54.

[3]冯国泰,黄家骅,王松涛.航空发动机数值仿真试验台建立中的几个关键技术问题的讨论.航空动力学报[J],2002(10):17-24.

[4]Beale D K,Zelenak M.Development and validation of a free-jet technique for inlet-engine compatibility testing[J].AIAA Paper No.92-3921,1992,AIAA 17th Aerospace Ground Testing Conference,Nashville,TN,1992:6-8.

[5]Hensel R W,Pindzola M.The design and development of a large supersonic free-jet test cell[J].The Aeronautical Jouanal of the Royal Aeronautical Society,1970,74:205-218.

[6]Mayward P V.C-2 Subscale Free-Jet Development and Demonstration,AIAA Paper No.93-2180,1993,AIAA/SAE/ASME/ASEE 29th Joint Propulsion Conference and Exhibit,Monterey,CA,1993:28-30.

[7]C.Lynn Sebourn,Frederick L.Shope research summary on the c-2 aeroacoustic resonance phenomenon,AIAA Paper No.2005-2932,2005,11th AIAA/CEAS/ Aeroacoustics Conference,Monterey,California,2005:23-25.

[8]王福军.计算流体力学分析[M].北京：清华大学出版社,2004:7-9.

[9]刘月玲,乔渭阳,许开富.S弯进气道内流分离数值仿真[J].计算机仿真,2010(10):29-34.

[10]赵承庆,姜毅.气体射流动力学[M].北京：北京理工大学出版社,1998:37-47.

[11]董志勇.射流力学[M].北京：科学出版社,2005.

[12]廉筱纯,吴虎.航空发动机原理[M].西安:西北工业大学出版社,2001:29-36.

[13]刘振侠,郭东明,张丽芬.S形进气道流场数值模拟[J].航空动力学报,2006(12):21-26.

[14]罗志煌,李军,刘超.某S型进气道总压畸变的数值模拟研究[J].微计算机信息,2010(26):6-11.

[15]夏杨,李博,王海明.一种两侧布局的无隔道亚声速进气道流场特性[J].航空动力学报,2013(2):28-33.

(责任编辑：宋丽萍 英文审校：刘敬钰)

The position relationship of nozzle-inlet duct in subsonic free-jet facility

WANG Jian-ling1a，XU Rang-shu1a,1b，KANG Jian2，ZHANG Zhao-rui1a

(a.Faculty of Aerospace Engineering;b.Liaoning Key Laboratory of Advanced Measurement and Test Technology for Aviation Propulsion System; 1.Shenyang Aerospace University,Shenyang 110136,China； 2.Sales Department,Jinan Diesel Engine Co.,Ltd,Jinan 250000,China)

To predict the characteristics of subsonic flow field before aircraft inlet-engine combination in the free jet test of engine altitude simulation and to optimize the aerodynamic configuration of the test cell,the CFD method has been used to conduct numerical simulation for the external flow of a fighter inlet under the condition of subsonic free-jet and the real flight environment.The result shows that if inlet was too close to the nozzle outlet,the similarity of the flow field may be dropped.And the flight Mach number,the angle of attack and the enginemass air flow will influence the best placement distance of inlet.

free jet;enginesimulation of altitude;inlet duct;position relationship;numerical simulation

2013-08-27

王键灵(1988-)，男，辽宁抚顺人，硕士研究生，主要研究方向：航空发动机数值仿真，E-mail:283410145@qq.com;徐让书(1962-)，男，浙江乐清人，教授，主要研究方向：航空发动机数值仿真，E-mail:xurangshu@yahoo.com。

2095-1248(2015)03-0012-06

V216.8

A

10.3969/j.issn.2095-1248.2015.03.003