转子临界转速计算的一维模型修正方法

王天胤，王克明，屈美娇，辛桂雨，郑喜洋

(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)

转子临界转速计算的一维模型修正方法

王天胤，王克明，屈美娇，辛桂雨，郑喜洋

(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)

采用有限元法，建立一维和三维模型计算一个转子的临界转速，在对一维模型计算结果进行误差分析的基础上，提出一维模型的修正方法。应用此方法建立了修正极转动惯量的一维模型并计算临界转速。通过比较计算结果发现，未修正一维模型的计算结果比三维模型的高，一阶临界转速最多高96%，二阶临界转速最多高50%，采用修正极转动惯量的方法对模型进行修正后，一阶临界转速最大偏差降低至5%，二阶临界转速最大偏差降低至0.7%，计算结果接近三维模型的计算结果。

转子系统；临界转速；有限元法；一维模型；模型修正

随着计算机技术和有限元软件的发展，有限元方法以其更高的求解精度和稳定性被广泛应用在转子系统动力分析上。但是在用于航空发动机整机计算时，有限元模型规模往往非常大，导致一般配置的工作站难以完成。解决这一问题常用的有效方法是对模型进行合理的简化，在保证计算结果满足精度要求的前提下三维实体有限元模型简化成一维有限元模型，减小模型规模，缩短计算时间，降低对计算机硬件的要求。本文通过分析一个简单转子系统一维模型计算结果的误差来源，提出一种一维模型的修正方法。应用此方法建模计算转子系统临界转速，一定程度上减小了计算误差。

1 一维模型计算结果的误差分析

1.1 有限元模型的建立

针对如图1所示结构，分别建立有限元一维与三维模型，如图2所示。模型由转轴轮盘以及轴承组成。材料的弹性模量为2.1×1011Pa，泊松比为0.3，密度为7.8×103kg/m3。三维模型盘、轴、叶片用Solid185、Solid186单元来模拟，轴承采用Combin214单元；一维模型转轴用Beam188单元模拟，轮盘以及叶片用Mass21单元以质量单元的形式加到盘在转轴的对应位置上，轴承采用Combin214单元。轮盘、转轴的模型参数见表1。

图1 转子模型示意图

图2 三维有限元模型示意图

表1 转子模型参数 m

经计算得到三维模型的一阶临界转速为1 614 r/min，二阶临界转速为4 492 r/min，一维模型一阶临界转速为1 711 r/min,二阶临界转速为4 533 r/min。

1.2 一维模型与三维模型临界转速对比

分别改变模型轮盘、叶片尺寸以及盘距轴左端的距离，建立有限元一维与三维模型，计算三维模型和一维模型的临界转速并对比。

叶片长为15 cm，盘距轴左端20 cm，轴尺寸以及支撑不变，改变轮盘的尺寸得到模型的临界转速如表2所示。

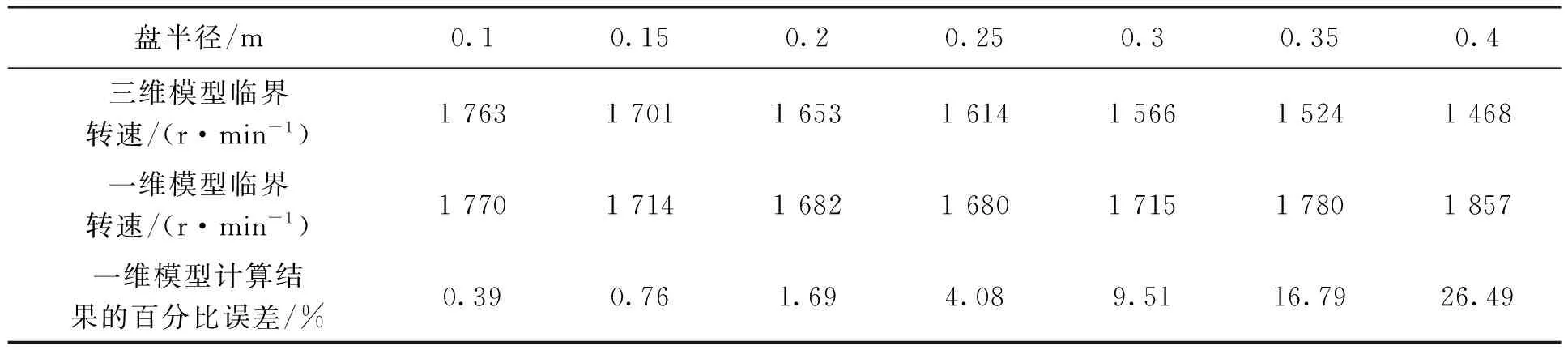
表2 不同轮盘尺寸的一维模型与三维模型临界转速以及一维模型计算结果的百分比误差

盘半径为25 cm，盘距轴左端20 cm，转轴尺寸以及支撑不变，改变叶片的尺寸得到模型的临界转速如表3所示。盘半径为25 cm，叶片长为20 cm，转轴尺寸以及支撑不变，改变盘在轴上的位置得到模型的临界转速如表4所示。从上述结果可以看出，随着轮盘与叶片尺寸的加大，三维模型与一维模型间的偏差加大；随着轮盘位置向轴的一端靠近，三维模型与一维模型间的偏差加大。当盘与叶片尺寸较大并且靠近轴左端时将转子模型直接简化成一维模型，得到的结果误差会很大。

1.3 一维模型临界转速误差来源分析

三维模型完全按照转子系统实际尺寸建立可以很好地解决模型的完整性问题，计算结果准确。一维模型中，转轴用一条直线代替，模型的盘与叶片通过质量单元Mass21来定义，赋予质量单元质量、极转动惯量、直径转动惯量，通过赋予的这几个量可以使Mass21单元近似代表轮盘与叶片，模拟计算出系统的临界转速。简化了的一维模型，盘以及叶片的变形无法体现出来，因此计算时存在一定的误差。由于离心力以及陀螺力矩的作用，三维模型叶片和轮盘在转动过程中会发生变形，变形后相当于改变了轮盘与公转轴的夹角，从而使陀螺力矩发生变化，最终影响临界转速，这便是一维模型与三维模型的主要误差来源。

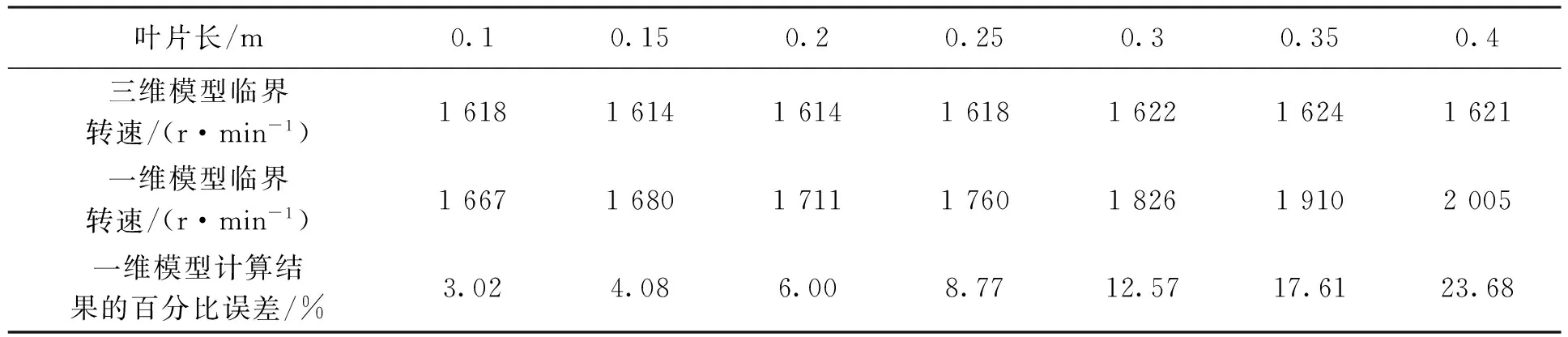
表3 不同叶片长的一维模型与三维模型临界转速以及一维模型计算结果的百分比误差

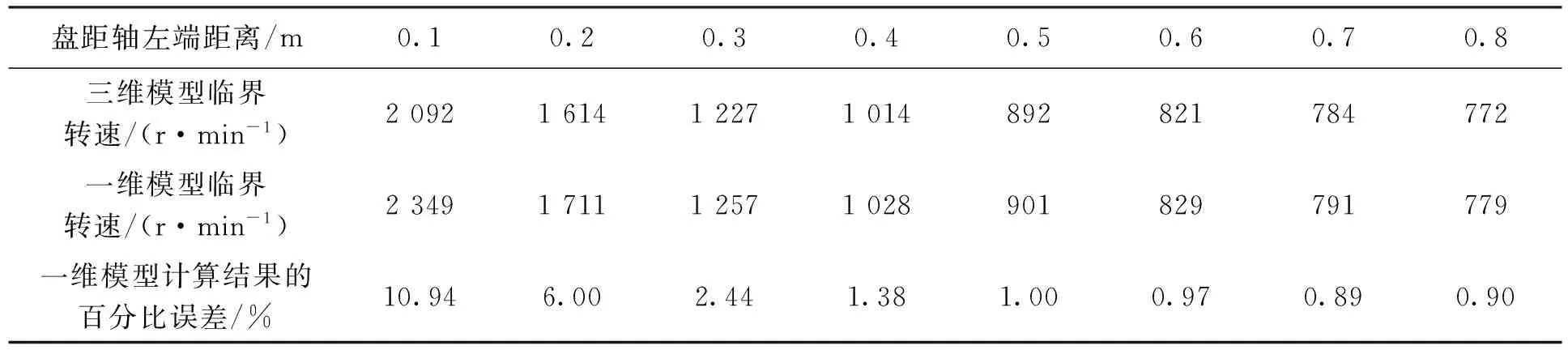
表4 盘在轴上不同位置的一维模型与三维模型临界转速以及一维模型计算结果的百分比误差

正进动时，在陀螺力矩的影响下，叶片和轮盘变形如图3所示，发生这样的变形相当于减小了轮盘与公转轴的夹角θ(0°<θ<90°)，从而使陀螺力矩减小，临界转速会降低。

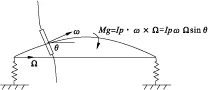
图3 正进动时轮盘叶片受力变形示意图

反进动时陀螺力矩会使轮盘以及叶片发生如图4所示变形，这样的变形相当于盘与公转轴的夹角θ(90°<θ<180°)减小，从而使陀螺力矩增大，临界转速降低。

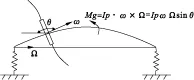
图4 反进动时轮盘叶片受力变形示意图

质量增大使系统临界转速降低，而转动惯量增大使系统临界转速提高。由表2.2可以看出，随着轮盘尺寸变大，轮盘以及叶片整体的质量以及转动惯量都增大，在一维模型中，临界转速呈现先减小后增大的趋势，起初临界转速受质量的影响临界转速降低，随后受到转动惯量的影响临界转速升高，而三维模型中由于存在轮盘与叶片的变形，实际上转动惯量对临界转速的影响相比质量对临界转速的影响起到的作用并不大，随着盘的尺寸变大三维模型的临界转速降低。

由表3可以看出，当轮盘尺寸不变、叶片的长度增大时，轮盘以及叶片整体的质量以及转动惯量都增大。在一维模型中，临界转速同样呈现先减小后增大的趋势，起初临界转速受质量的影响比较明显临界转速降低，随后受到转动惯量的影响比较明显临界转速升高。然而三维模型中由于存在轮盘与叶片的变形。实际上转动惯量对临界转速的影响与质量对临界转速的影响大体相当，这个变化与单独加大盘的尺寸时情况不同。由于叶片与轴心的距离相对于轮盘与轴心的距离要大。增加叶片长度时，随着叶片质量的增加，转动惯量的增量要比轮盘质量增加时转动惯量的增加要大。因此，在增加叶片长度时，三维模型的临界转速变化不明显。由表4可以看出，轮盘距离轴一端越近，转轴旋转变形后，轮盘与转轴间的夹角越大，陀螺力矩越大，三维模型中盘及叶片受陀螺力矩影响而产生的变形越大。因此，当盘的位置越靠近轴一端时，三维模型与一维模型间的偏差越大。

由此可见，轮盘、叶片变形造成盘与公转轴夹角的变化影响了陀螺力矩，从而影响系统的临界转速。轮盘叶片的变形三维模型能够体现出来而一维模型无法体现，这是造成三维模型与一维模型间误差的主要原因。如果能够修正一维模型中质量单元的参数，使一维模型的陀螺力矩变化趋势与三维模型变形引起的陀螺力矩变化趋势相同，将会减小一维模型与三维模型之间的误差。同时，三维模型的变形也与叶片、轮盘的形状有关，不容易变形的叶片、轮盘结构更加接近于刚体，与一维模型的处理更加相近，这样的三维模型与一维模型间的误差会相对较小。

2 转子一维模型的修正

为了减小三维模型与一维模型临界转速的偏差，可以通过调整一维模型中Mass21单元的质量和转动惯量来实现。由上述分析可知，三维模型变形后轮盘与转轴的夹角发生变化，从而影响陀螺力矩，最终影响系统的临界转速，这是三维模型与一维模型之间的主要偏差。Mass21单元中的质量变化能够影响系统的固有频率，调整Mass21单元的质量会改变系统的固有频率，通过改变固有频率来调整临界转速不合理，因此，不能通过调整Mass21单元中质量系数来减小误差。极转动惯量是影响陀螺力矩的因素，修正Mass21单元的极转动惯量将会引起陀螺力矩的变化，虽然不能通过一维模型表现出三维模型变形后夹角的变化，但是可以通过改变极转动惯量来实现一维模型的陀螺力矩与三维模型变形后的陀螺力矩相一致。因此本文采用修正Mass21单元的极转动惯量的方法来减小一维模型与三维模型间的误差。

2.1 单盘转子的一维模型修正

建立如图1所示单盘单轴结构的三维模型以及一维模型，固定盘在距轴一端10 cm位置处，计算临界转速，调整一维模型的极转动惯量，使一维模型的临界转速与三维模型一致。得到修正后的极转动惯量后，分别找出不同盘尺寸及叶片尺寸模型修正后的极转动惯量，得到相应的修正系数(修正系数=修正后的极转动惯量/模型实际的极转动惯量)，结果如表5所示。此方法得到的修正系数只适用于轮盘在距轴左端10 cm的位置，如果对在转轴上其他位置的轮盘进行修正，则要固定转盘在转轴的其他位置，用此方法找到修正系数。

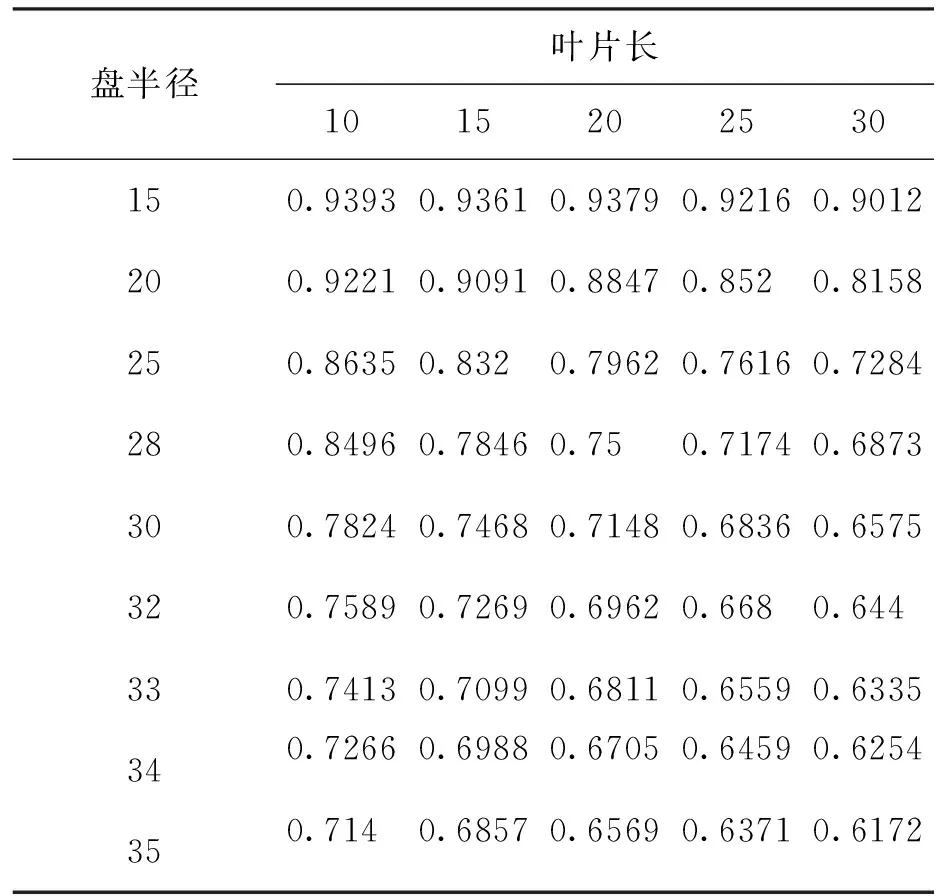
表5 修正系数随轮盘叶片尺寸变化 cm

由表5可以看出，随着轮盘、叶片尺寸的增大轮盘叶片更加容易变形。转子转动时，变形更加剧烈，一维模型与三维模型间误差更大，模型的轮盘、叶片尺寸越大，修正后的极转动惯量越小，修正系数越小。建立如图5所示的双盘转子结构的三维模型和一维模型，保持材料参数以及转轴参数不变，两个盘的位置在距轴一端10 cm的对称位置上。

为了验证这种修正方法的合理性，应用图1中单盘结构得到的修正系数，将修正系数应用在图5所示的双盘结构上。选取3种轮盘叶片参数建立双盘结构修正后的一维模型，分别计算3种模型一阶正进动型临界转速以及相对于三维模型的转速差和计算结果百分比误差。对比结果如表6所示。

由表6可以看出，未经修正的一维模型临界转速与实际三维模型的临界转速偏差较大，修正后的一维模型临界转速与三维实体模型的临界转速计算结果偏差较小。

图5 双盘转子模型示意图

2.2 双盘转子的二阶临界转速修正

图5所示的双盘结构由轮盘引起的临界转速有两阶，对于第二阶临界转速的修正方法采用如下方案：将双盘模型从转轴中间位置截断，将截面中心节点位移全约束，不限制其扭转，左侧支撑保持不变，结构简图如图6所示。图6所示的一阶弯曲临界转速的振型与图5所示左半部分二阶弯曲临界转速振型一致。将图6一阶临界转速修正系数作为图5双盘结构左侧盘的修正系数，由于算例模型是轴对称的，因而右侧盘的修正系数与左侧盘一致。

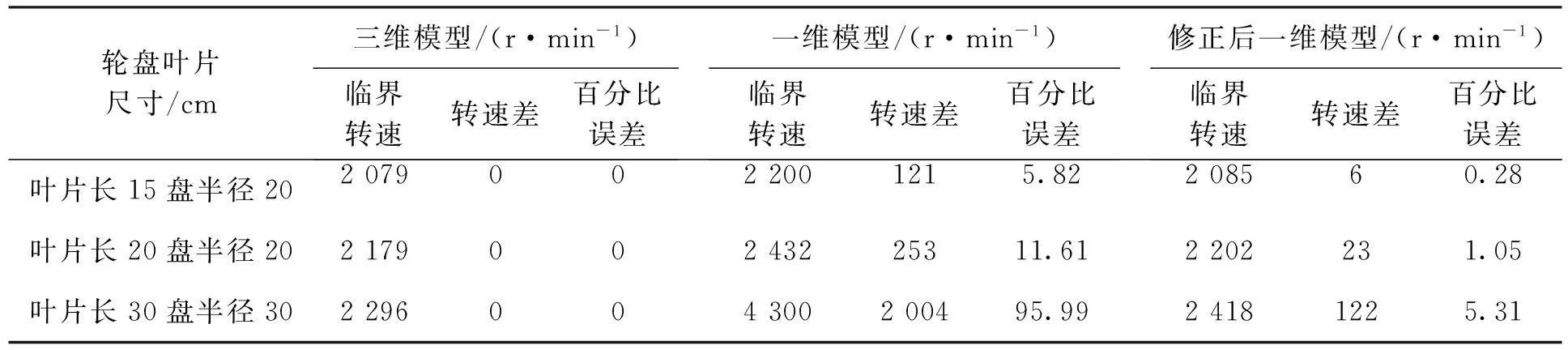
表6 不同尺寸模型一阶正进动临界转速对比

图6 一端简支一端固支转子模型示意图

将图6中得到的修正系数应用到图5结构中来验证修正方法的合理性。选取3种轮盘叶片参数建立如图5所示双盘结构一维模型、三维模型以及应用修正系数修正后的一维模型，分别计算三种模型二阶正进动型临界转速，对比结果如表7所示。

由表7可以看出，未经修正的一维模型临界转速与实际三维模型的临界转速偏差较大，修正后的一维模型临界转速与三维实体模型的临界转速计算结果偏差较小。

3 结论

由于离心力及陀螺力矩的作用，三维模型叶片以及盘在转动过程会发生变形，这种变形一维模型无法体现，轮盘叶片发生变形后相当于盘与公转轴的夹角发生变化，从而使陀螺力矩发生变化，影响到临界转速，这是一维模型与三维模型的误差主要来源。

(1)随着轮盘与叶片尺寸的加大，三维模型与一维模型间的偏差加大，随着轮盘位置向轴一端靠近，三维模型与一维模型间的偏差加大。当盘与叶片尺寸较大并且靠近轴一端时直接将转子模型简化成一维模型，得到的结果误差会很大。

(2)从计算可知，直接将轮盘以及叶片简化成质量单元进行建模，计算结果与三维模型相比一阶临界转速最大偏差达到96%，二阶临界转速偏差达到50%，计算结果非常不合理。

(3)采用修正极转动惯量方法对模型进行简化与对三维模型直接进行一维简化相比，采用修正极转动惯量的方法简化模型计算出的临界转速误差较小，一阶临界转速最大偏差降低至5%，二阶临界转速最大偏差降低至0.7%。

[1]张力，洪杰，马艳红.航空发动机转子系统建模方法和振动特性分析[J].北京航空航天大学学报，2013，39(2)：148-163.

[2]孟光.转子动力学研究的回顾与展望[J].振动工程学报，2002，15(1)：1-8.

[3]王超，王延荣，徐星仲.应用三维有限元法计算汽轮机转子临界转速和模化长叶片[J].动力工程，2007，27(6)：840-844.

[4]韩清凯，于涛，王德友.故障转子系统的非线性振动分析与诊断方法[M].北京:科学出版社，2010.

[5]陈萌，马艳红，刘叔国.航空发动机整机有限元模型转子动力学分析[J].北京航空航天大学学报，2007，33(9)：1014-1016.

[6]梅庆.二维有限元模型在燃气轮机转子-支承系统临界转速计算中的应用[J].燃气涡轮试验与研究，2003，16(3)：42-44.

[7]Hsiao-Wei D.Chiang，Chih-Neng Hsu，Shun-Hsu Tu.Rotor-bearing analysis for turbomachinery single-and dual-rotor systems[J].Journal of Propulsion and Power，2004，20(6)：1096-1104.

[8]钟一锷，何衍宗.转子动力学[M].北京：清华大学出版社，1989.

[9]缪辉，王克明，翟学.反向旋转双转子系统动力学特性的有限元分析[J].沈阳航空航天大学学报，2011，28(4)：27-31.

[10]朱向哲，袁惠群，贺威.稳态温度场对转子系统临界转速的影响[J].振动与冲击，2007，26(12)：113-116.

[11]张婷婷，王克明，孙阳.温度场对双转子系统动力特性影响的分析[J].沈阳航空航天大学学报，2013，30(1)：34-38.

[12]刘长福，邓明.航空发动机结构分析[M].西安：西北工业大学出版社，2006.

[13]朱向哲，贺威，袁惠群.稳态温度场对转子系统振动特性的影响[J].东北大学学报(自然科学版)，2008，29(1)：113-116.

[14]艾书民，王克明，缪辉.稳态温度场作用下涡轮叶片振动特性的研究[J].沈阳航空航天大学学报，2011，28(4)：17-21.

[15]李玲玲，王克明.某型航空发动机后支承动刚度的有限元计算[J].沈阳航空航天大学学报，2007，24(3)：5-7.

(责任编辑：宋丽萍 英文审校：刘敬钰)

Study on the correction method of one-dimensional model for rotor critical speed calculation

WANG Tian-yin，WANG Ke-ming,QU Mei-jiao,XIN Gui-yu,ZHENG Xi-yang

(Faculty of Aerospace Engineering,Shenyang Aerospace University,Shenyang 110136,China)

By finite element method,critical speed of a rotor system is calculated using one-dimensional model and three-dimensional model respectively.Based on the error analysis of the calculation results,a correction method of the one-dimensional model is proposed.This method is used to construct the one-dimensional model with the moment of inertia and then calculate critical speed.The comparison of the calculation results shows that the computation outcome of the one-dimensional model without correction is higher than that of the three-dimensional model.In extreme condition,the first critical speed can be 96% higher,and the second critical speed can be 50% higher.After modifying the moment of inertia of the one-dimensional model,the maximum deviations of the first and the second critical speeds reduce to 5% and 0.7% respectively.The calculation results of modified one-dimensional model are close to results of the three-dimensional model.

rotor system;critical speed;FEM;one-dimensional model;model correction

2014-12-01

王天胤(1987-)，男，辽宁沈阳人，硕士研究生，主要研究方向：航空发动机强度、振动及噪声，E-mail：wangtianyin0711@163.com；王克明(1954-)，男，辽宁沈阳人，教授，主要研究方向：航空发动机强度、振动及噪声，E-mail：wkm308@126.com。

2095-1248(2015)03-0006-06

V211

A

10.3969/j.issn.2095-1248.2015.03.002