谈提高笔算除法教学有效性的策略

2015-02-15浙江省绍兴市上虞区樟塘小学张春燕

新课程研究 2015年11期

关键词：笔算竖式学具

◆浙江省绍兴市上虞区樟塘小学张春燕

谈提高笔算除法教学有效性的策略

◆浙江省绍兴市上虞区樟塘小学张春燕

三年级下册“笔算除法”教学看似轻松，实则不易。文章首先从学生层面、教师层面、教材层面分析原因，然后从合理使用教材、合理使用教学手段、加强后续练习3方面寻求策略，提高“笔算除法”教学的有效性。

笔算除法；分析；策略

一、缘起

教学实验课程 “人教版”三年级下册的 “除数是一位数的笔算除法”内容之前，笔者完全没有想到这一单元如此曲折坎坷，不仅在课堂上出现了教学时间不够、教学过程牵强、教学效果极不理想等问题，而且在这一单元快上完时，笔算除法中漏写、商错位置、数位不对齐、不会商0等问题依然比比皆是。无论怎么安排练习，仍然无法扭转乾坤，反思势在必行。

二、溯因

1.学情和教材分析

（1）教材纵向分析。实验版教材三年级下册的 “除数是一位数的笔算除法”在三年级上册 “两位数除以一位数”的基础上进行教学，该部分的内容是 “表内除法”和 “有余数的除法”。到了三年级下册，这块内容升级了，虽然还是 “除数是一位数的除法”，但笔算难度大大增加，为四年级学习 “除数是两位数的除法”奠定基础。

（2）教材横向分析。实验版教材三年级 “除数是一位数的除法”，教材先是安排口算除法，再是估算，接着才是笔算除法。笔算内容包括了两位数除以一位数、三位数除以一位数的所有情况，而教材建议13课时进行教学，如此多的内容，如此大的跳跃性，对学生学习这一部分知识提出了较大挑战。

2.原因分析

（1）学生层面。

第一，算理模糊。很多错误是因为学生对竖式意义不理解，出现的漏写商（如图1）、不会商（如图2）、忘写余数（如图3）、不会商0（如图4）都是因为脱离了除法竖式平均分的主旨及数位位值意义的理解。如图1，7个10减去6个10剩下1个10，和个位上的5合起来是15，然而接下来学生抛开了 “再将15平均分成3份，每份是5”的算理，只为了写竖式而完成竖式，在没有算理的支撑下必定会产生问题。

第二，书写格式错误。学生受经验的影响，计算难度不大的除法题时，更愿意口算而非笔算，大部分学生就出现了“答案口算，竖式照样填空”的问题，而不拘泥于形式地一步一步地计算（如图5）。在图6中，学生对除法竖式的基本步骤一商、二乘、三减的应用能力不足。虽然答案是正确的，但不正确的书写格式对于学生的后续学习不利。

图1

图2

图3

图4

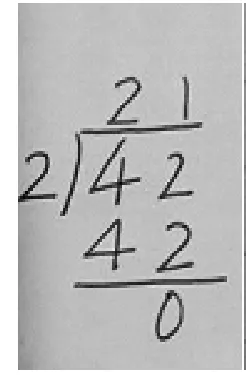
图5

图6

（2）教师层面。

第一，忽略算理的重要性。一般教师认为，除法竖式只要传授给学生一商、二乘、三减、四比、五落的技能就万事大吉了，事实上学生在没有理解的基础上学习技能，效果并不理想。有些教师虽然意识到了，在教材 “一位数除两位数”的两个例题中利用小棒图帮助学生学习除法竖式的写法，但教师只让分小棒的过程走过场，却未能与算理进行密切沟通，辅助效果不大。

第二，过于放大练习功能。如果学生对笔算除法的算理缺乏理解，面对多种笔算情况，学生很难进行同理沟通，即使教师安排再多的练习，问题依然顽固不化，练习—订正—再练习，这个简单的措施对学生掌握笔算除法的帮助并不显现。

（3）教材层面。

第一，缺乏循序渐进。口算是笔算的基础，但教材在第1课时安排的口算内容是一位数除以商是整十、整百、整千的数，一位数除几百几十（或几千几百），像 “42÷2= 21”这样的口算题却未涉猎，其基本口算方法实际是笔算的基础，所以学生也就没有基本口算方法的体验，在这样的基础上学习笔算，对学生来说少了知识的支撑点。笔算先学一位数除两位数，巩固了两节课，学生基本会做了，教材就开始安排学习一位数除三位数，事实上被除数增加一位，不仅是除的时候多了一步，题目的变化也更多了。例如，被除数第一位够除的，不够除的，实验教材把这些情况都安排在同一节课中，缺乏阶梯性和层次性。学生因做题时感觉不大一样，又缺少一个理解和逐步接受的过程，给学生掌握这部分知识带来了一定的影响。

第二，过于依赖生活情境。统观这一单元的教材，笔者发现几乎一致的教学流程：创设情境—提出问题—解决问题（列式）—再对解决问题的方法进行教学（计算）—实践应用。如此标准的流程麻痹了教师对新知、重难点的警觉性，导致过于依赖教材，缺乏深入地思考和分析。一个情境列一个算式，一种情境还有多种解题策略，一堂课下来，学生只做了四五道练习。

三、策略

1.合理使用教材，迎合学生认知

（1）摒弃部分教材要求，直击主题。教材想要达成多元目标，恐怕只是教育者的一个美好理想。一节所谓的计算课被生活情境占了大部分时间，分散了学生的注意力，转移了学生学习新知的兴奋点，一定程度上弱化了计算技能的掌握。的确，芝麻绿豆西瓜兼得，顾此失彼乃属正常。所以，有时不妨尝试一下计算教学与解决问题分离，抓住重点，直击主题。特别是对上述实验教材第22页的内容、重点和难点都是除法竖式的书写格式及除法竖式的意义理解上，所以在教学时间非常紧张的情况下，索性上一堂纯计算教学课，再用所学的技能去解决情境中的问题。

（2）重组教材内容，逐层深入。因之前对教材第22页三位数除以一位数的教学出现严重失误，所以对这部分内容进行较为用心地设计，以便能更早、更好地弥补教材或学生的缺失。

教学新课前，设计一组复习题练习 “24÷2”和 “54÷ 3”。设计 “24÷2”是为了帮助学生进一步明确除法竖式的正确书写格式，可以有效避免口算的影响，在进一步理解算理的基础上明确 “笔算除法需要从最高位除起，依次计算”。而设计 “54÷3”的价值在于除了让学生进一步明确正确的除法书写格式外，还可以让学生复习巩固 “当最高位除后有余，余下来的数要各个位上的数合并继续除”这一计算方法。

教学新课时，先出现 “三位数除以一位数每一位上的数正好能整除”的类型，如248÷2，让学生独立尝试解决，在解决的过程中学会计算方法的迁移，明确从最高位算起，依次计算。接着出现 “238÷2”，让学生在计算过程中明确算理和算法。第三层次再出现与例题同类型的题目 “238÷ 6”，通过 “238÷2”和 “238÷6”对比思考 “百位不够除怎么办”的问题。如此步步为营、层层深入，有效分解了学生的学习难点。

2.合理利用教学手段，有效沟通算理

（1）准确切入，突破新知难点。之前在教学两位数除以一位数的笔算除法时，用三年级上册的表内笔算除法进行引入，但却毫无预料地将这节新课拖入泥潭之中，让学生在复习旧知的基础上尝试笔算。如 “42÷2”，结果发现绝大部分学生受经验迁移的影响，都将笔算写成了如图5的算式，在探索无果的情况下，笔者再进行正确笔算格式的教学，期间有不少学生还是难以接受这样的笔算方法，还有部分学生质问： “为什么一定要这样写？”笔者无言以对，只是硬着头皮照着自己的思路走完教学流程。课后思考，为什么惯用的 “旧知铺垫”在这里反而成了推进新课的绊脚石？只好重新翻阅教材，细细斟酌，不难发现两位数除以一位数商是两位数的笔算是以摆小棒和口算除法作为经验进行迁移的。教育心理学认为，学习对象之间的共同因素是迁移的基本条件，共同因素越多，迁移就越容易。的确，只要稍加思考就不难得出结论：一位数除两位数的笔算方法，不能成为探索一位数除两位数商是两位数的笔算除法的正迁移。因为前者的运算步骤只有一步，而后者却有两步，相差甚远。所以，后来再上这节课，笔者特别注重以下几点：

第一，由口算方法向动手操作迁移，建立直观形象的笔算方法。学生根据情境提出了数学问题：三年级两个班共植树42棵，平均每班种多少棵树？学生得出口算方法“40÷2=20（棵）” “2÷2=1（棵）” “20+1=21（棵）”后，教师要求学生用摆小棒的方法来说明口算步骤。学生独立思考后交流：先摆出4捆（每捆10根）和零星的2根，第一步把4捆平均分成两份，每份2捆，也可以说每份20根；第二步把剩下的2根小棒平均分成两份，每份1根。教学时，教师引导学生紧紧抓住分小棒的操作要领：先分整十的，再分余下的，即把52根小棒中的4捆平均分成2份，每份是2捆，再把余下的1捆拆开与2根合起来是12根，平均分成2份后每份是6根。这样教学既以口算为基础，又为学生构建笔算方法提供了直观、形象的感性材料。

第二，由口算、摆小棒的方法探索向笔算方法迁移，促进学生思维方式的转变。首先，教师让学生把口算步骤和摆小棒的方法在笔算中表示出来。学生独立探索后，沟通直观图与抽象计算之间的联系，做到顺利迁移，师生共同得出正确的笔算方法，如图7。这样的教学采用了解题策略间的迁移——口算、摆小棒的步骤与探索笔算方法相结合，不仅为学生搭建了探索笔算方法的阶梯，保证了探索活动的有效性，而且促进了学生形象思维向抽象思维的转变，解决了思维跳跃性过大的难点。

（2）学具操作，强化算理体验。学具是为了加强直观印象，让学生体验算理而设。但是，以往笔者总担心教学时间不够，时常代替学生操作学具，无法让每个学生都能有体验的机会。再上一位数除两位数时，让每个学生充分操作学具，深刻体验两位数怎么分，才能对后面的竖式教学产生正迁移效果。不到火候，等于白操作，后面的竖式仍然很难让学生接受。虽然在学具操作环节花了较多功夫，看似费时却对竖式教学产生了积极的影响。学具操作要以学生的体验为尺度，而不是以教师的教学时间为尺度，要让操作起到辅助学习的作用，而不是唱唱花腔、过过场。教学 “256÷6”时，虽然教材已脱离学具操作这根拐杖，但根据学情仍然可利用课件出示小棒图帮助学生理解算理。

在之后的商中间和末尾有0的除法教学中，学生常对“为什么商0”产生疑问，在过于抽象学生理解有困难的情况下不妨再回到具体，适时联系学具操作。例如，教学商末尾有0的除法 “562÷4=140……2”时，为什么个位不够除时商0？余下的2该怎么办？当学生难以表达的时候，教师适时画出小棒图和零星的两根小棒，如图8。

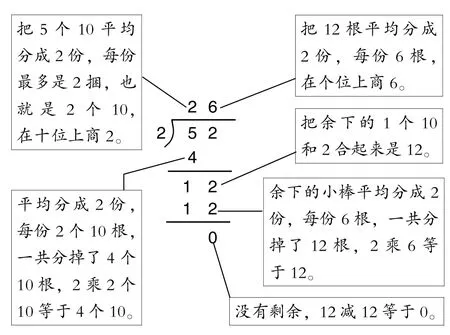
图7

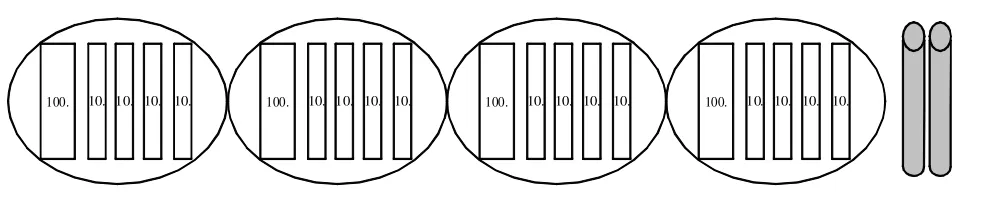
图8

这两根小棒还能平均分成4份吗？不能！就只能剩下，而每一份只能是140根小棒，所以个位上只能商0。其实，教师常常忽略的就是点拨，学生不可能像成人一样 “由此及彼”。将这个比较抽象的知识点与具体事物联系起来，容易引起共鸣，也能让学具操作适时发挥作用。

（3）语言内化，提升抽象能力。心理学认为，用简明的词语来表述复杂的事物或记载分析的成果，有助于简缩思维过程和不断地抽象、概括。语言是思维的工具，语言内化的过程既是知识的内化过程，也是思维的提升过程。同时，要考虑学生之间的差异，有些可能没听见，有些可能没有完全领会，可以多说几遍，先教师引领说，再学生个别说、集体说等。

3.加强后续练习，提高笔算正确率

（1）加强纠错练习。许多教师和家长把学生做错题一律归因为 “粗心”，其实不然。教师应客观对待学生的错题，教学过程中笔者随时收集错例并进行比较分类，因为学生的错题有时也是教学效果的如实反映。当某一种类型出现同一种错误时，教师应采用自我纠错和集体纠错相结合的方式反思自己的教学行为，及时采取措施。

（2）加强比较练习。学生应对随时出现的各种不同情况的笔算除法时，会出现混淆现象，教师应有意识地多进行比较练习，有助于学生更好地理解算理和掌握技能。

（3）加强验算习惯的培养。验算从计算中来，是二次计算，能提高学生做题的正确率，重点是让验算成为学生的一种自觉行为。这一单元中教材也安排了利用 “商乘除数加余数等于被除数”作为除法的验算，但要求学生每道题都用这种方法验算是不现实的。笔者认为，应让验算行为成为学生的内在需要，而不是教师的强加行为。

验算方法也可以因题、因人而异。在集体纠错练习中，投影出示如图竖式，请学生先判断对错，一个学生说（如图9）： “被除数的第一位够除，所以我认为商一定是三位数，而它是两位数，所以这一题肯定是错的。”另一个学生说（如图10）：“把605估成600除以5，结果也有120，正确的答案应该比120还要大，所以101肯定是错的。”教师可以引导学生： “是啊，在自己做题的过程中，也用这样的方法进行验算，相信你的笔算除法还能做得更好！”