量子力学和分子力学组合方法

谢湖均雷群芳方文军

(1浙江工商大学应用化学系 浙江杭州310035;2浙江大学化学系 浙江杭州310027)

2013年诺贝尔化学奖10月9日在瑞典揭晓，法国斯特拉斯堡大学和美国哈佛大学教授Martin Karplus、美国斯坦福大学医学院教授Michael Levitt和美国南加州大学教授Arieh Warshel因发展复杂化学系统的多尺度模型而共享奖项［1-2］。以前化学家是用塑料的球和棍来搭建和创造分子模型，而现在则是用计算机来辅助建模和计算。分子和化学反应的精确建模对于化学的进步至关重要，化学反应的速度非常快，在几分之一毫秒间，电子就会从一个原子核跳到另一个原子核，经典化学在这里已无用武之地。Karplus、Levitt和Warshel工作的突破意义在于他们设法让量子力学(quantum mechanics，QM)和分子力学(molecular mechanics，MM)结合在化学过程的建模之中。量子力学计算方法可以用来预测电子结构和化学反应机理，精确度很高，但只能用来计算较小的体系。而分子力学的优势在于计算简便，虽然可以用来计算较大的复杂体系，但精确度不够高，而且无法描述化学键生成或断裂的化学反应过程。他们3人的工作结合了两者的长处，发展出量子力学和分子力学组合方法(combined quantum mechanics/molecular mechanics method，QM/MM)。QM/MM组合方法在大分子体系的计算研究中已展现出越来越强大的功能，已经逐步应用到化学、材料、生物学等各个相关学科领域［3-8］。本文就其基本原理和目前的研究进展做简单的介绍。

1 QM/MM组合方法基本原理

1.1 QM/MM组合方法的能量表达式

如图1所示，QM/MM组合方法的主要思想是把整个体系分为QM和MM两部分，其中QM部分用量子力学方法处理，MM部分用分子力学方法处理，QM和MM的边界则用连接原子或冻轨道等方法处理。目前流行的QM/MM能量表达式有两种，加和方法(additive schemes)［9-10］和减去方法(subtractive schemes)［11-13］。在一般的计算中采用的是加和方法，其能量表达式为:

这里的EQM和EMM分别为单独QM和MM部分的能量。EQM-MM为两个区域的耦合项。原理上任何的量子力学方法都可以用来处理QM部分，但是在文献中报道的一般都是DFT和半经验理论计算的结果。

这种能量的加和方法在QM/MM组合计算中广泛采用，尤其是在生物大分子领域。目前可以使用的软件包主要有CHARMM［14-15］和AMBER［16-17］。但是此方法也存在着问题，由于存在连接原子［18］，耦合项EQM-MM不易计算。

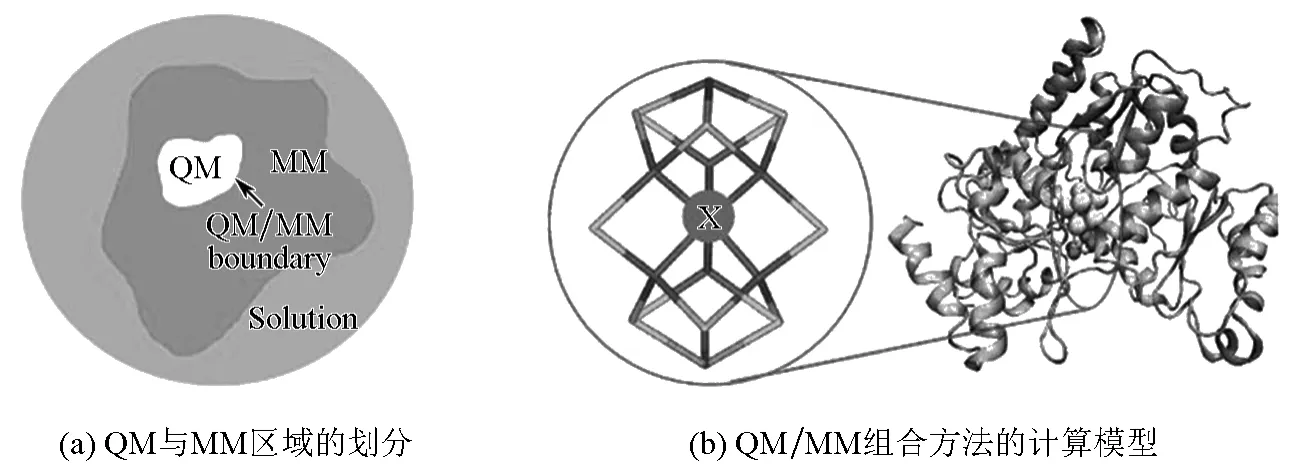
图1 QM/MM组合方法示意图

1.2 静电势项

QM区域电荷密度和MM区域电荷模型之间的静电势耦合作用，可以在不同的计算水平下进行，主要的区别是QM和MM区域相互极化的作用范围。为此，Bakowies和Thiel定义了3种处理静电势相互作用的方法［19］。

1.2.1 机械嵌入(mechanical embedding)

在这种方法中，QM区域的计算本质上是在气相中进行的，缺乏与环境之间的耦合作用。QM与MM区域静电势的相互作用或者被遗漏，或者仅仅在MM水平上计算。计算时一般采用刚体的点电荷模型。对于其他的方法，例如键偶极方法也在QM部分使用。Morokuma提出的ONIOM模型即采用这种机械嵌入方案来处理QM与MM区域间的静电耦合。

但是，在这种方法的应用过程中，存在明显的缺陷和限制。(1)外层的电荷不与QM区域的密度相互作用，使QM部分不能直接被静电势环境所影响;因此，QM区域的密度没有被极化。(2)对于QM区域的电荷分布，例如在反应过程中，电荷模型需要不断地更新;但是，这又会导致势能面的不连续性。(3)采用MM点电荷来处理内层区域所产生的偏差是不能忽略的;一般在程序中，都有很多种力场来处理这些体系，选择时需要慎重考虑，因为一般力场的发展与这些具体的化合物没有联系。(4)MM的电荷模型依靠其他的力场参数，这就意味着最后产生的构型是平衡态的描述，而不是重新产生的真实电荷分布。

1.2.2 静电场嵌入(electrostatic embedding)

在此方法中，MM区域电荷分布对QM区域所产生的极化作用，可以看作是QM区域电子结构计算的一部分，因此能够克服机械嵌入方法的缺点。其表达式为:

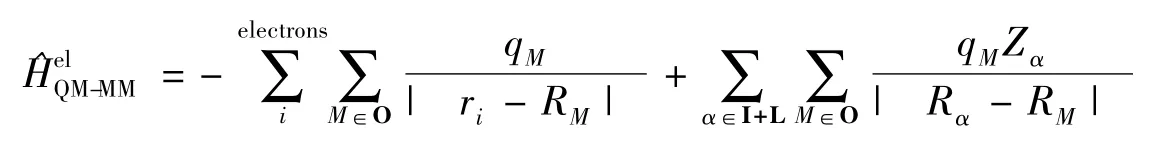
这里qM为MM区域点电荷，Zα为QM区域原子的核电荷，i是电子总数，M是总的点电荷，α为QM区域所有的核。

在静电场嵌入方法中，内层区域的电子结构可以适应环境电荷的变化，并且被环境所极化。这里的静电势是在QM水平下计算的，相对于机械嵌入方法，明显提高了精度，当然计算的代价也会更大。

使用静电场嵌入方法，需要注意的地方是处理QM/MM的边界区域，此时MM的电荷非常接近QM的电子密度，会导致过度极化问题，这在边界区域是共价键时更加显著。目前，静电场嵌入是生物大分子计算中最流行的方法。

1.2.3 极化嵌入(polarized embedding)

此种方法在静电场嵌入的基础之上，又包含了QM区域电荷分布对MM区域所产生的极化影响。尽管极化嵌入是最精确的方法，但是对于它的应用范围，仍然是非常有限的。主要的问题在于还没有建立起合适的生物大分子极化力场。目前，有许多极化的溶剂模型可以采用，最显著的就是液态水的模拟。对于蛋白的极化力场，还在进一步的发展中。当然，这种方法的应用，也会增加计算的代价，还有可能造成收敛问题。目前常用的极化嵌入方法有polarized point dipoles(PPD)，drude oscillators(DO)和fluctuating charges(FQ)。

1.3 其他的非键和成键相互作用

除了上面部分讨论的静电势相互作用，还有范德华和成键相互作用贡献到QM/MM的耦合项。它们的处理比较简单，一般都在分子力学的计算水平下。范德华相互作用一般采用经典的Lennard-Jones势:

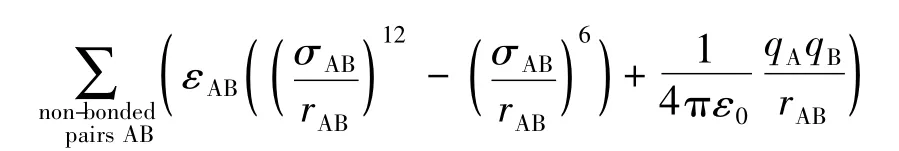
Friesner等发展的QM/MM组合方法［20］，根据氨基酸模型中氢键的几何结构和键能，重新优化了QM区域的范德华相互作用参数。此时得到的范德华半径要比OPLS-AA力场大5%～10%，而范德华势阱深度则没有改变。增加的范德华排斥用来补偿由于MM点电荷引起的QM密度过度极化。最近崔强等［21］提出，在QM/MM组合方法下计算得到的固相热力学数值，对QM/MM范德华参数不敏感。

对于成键相互作用，需要采用合理的方案来处理，避免出现双重计算。一般的规则是每一个成键项要依靠内层和外层的原子。

1.4 QM/MM组合方法对边界原子的处理

对于边界原子的处理，一般不可避免会碰到共价键断裂的情况。断键的原理一般是不要涉及到键的耦合项，最好是极性的，没有共轭相互作用。处理的方法具体可以分为3类。连接原子方法(linkatom schemes)［18］，边界原子方法(boundary-atom schemes)［22-25］和定域轨道方法(localized-orbital schemes)［26-28］。

连接原子方法引进了额外的原子中心(通常为H原子)，而这并不是真实系统的一部分。它的引入，增加了人为的自由度，使得结构优化过程更加复杂。虽然存在缺点，但是此种方法仍旧是最流行最广泛应用的边界原子处理方法。而我们的QM/MM组合方法计算中采用的也是这种方法。

在边界原子方法中，MM边界的一个原子被一个具有两性的原子所代替，它可以同时出现在QM和MM的计算中。大多数提出的边界原子方法，都是建立在单价赝势的基础上，通过参数化来得到所期望的性质。目前常见的方法有adjusted connection atoms［22］，pseudobonds［23-24］和effective group potentials［25］。

定域轨道方法把有方向性的杂化轨道放在边界原子处，并使其中的一些轨道冻结，不参与自洽迭代。主要的方法有local self-consistent field(LSCF)［26］，frozen orbitals［27］和generalized hybrid orbitals(GHO)［28］。

1.5 自由能计算

计算得到的体系自由能可以与实验得到的数据相比较，因此体系自由能的计算是QM/MM组合方法中的一个重要环节。在描述化学反应的过程中，自由能计算充分考虑了研究体系的涨落(fluctuation)情况，比静态的电子结构计算获得的相对能量值更具有物理意义。在QM/MM计算水平下，为了得到体系的自由能曲线，常用的方法一般有两种:(1)自由能微扰(free energy perturbation，FEP)［29］;(2)热力学积分(thermodynamic integration，TDI)［30］。在处理近过渡态区域的分子构象时，通过正常的非限制性QM/MM MD方法可能找不到高能区域的构象。因此在研究反应的过渡态时，伞形采样(umbrella sampling，US)方法［31-32］被广泛用于高能区域采样。一般WHAM分析方法［33］可以与伞形采样相结合，最终计算得到反应的自由能曲线。

1.6 QM/MM组合方法的计算方法架构

QM/MM组合方法的使用具有强大的柔性，计算中能够采用各种各样的QM和MM计算方法。在实际应用中，许多生物大分子的QM/MM组合计算都采用半经验作为QM区域的计算方法，用DFT的情况相对较少。对于MM部分，现在采用的都是建立在点电荷模型之上的价力场，到目前为止，还没有合适的极化力场可以广泛运用。普遍运用的生物大分子力场主要有CHARMM［14-15］，AMBER［16-17］，GROMOS［34-35］，OPLS-AA［36-38］;而普通的力场则有MM3［39-40］，MM4［41-42］，MMFF［43-44］和UFF［45］。

目前，流行的QM/MM组合计算的软件包有3种:(1)在MM的软件包中加入QM部分的计算，常见的软件包有AMBER和CHARMM;(2)在QM的软件包中加入MM部分的计算，常见的软件包有ADF，GAMESS-UK，Gaussian，NWChem，QSite/Jaguar，Car-Parrinello MD codes with QM/MM capabilities，CPMD，CP-PAW;(3)耦合已经存在的QM和MM的程序包，常见的软件包有ChemShell，QMMM和Q-Chem/Tinker。

2 QM/MM组合方法研究进展

自从1976年Warshel和Levitt提出杂化QM/MM的概念［2］，并将其用于研究溶解酵素的反应机理以来，许多课题组相继提出了不同的QM/MM组合方法，已广泛应用于各类相关的化学、生物学和材料等问题。Kollman小组［46］开发了AMBER软件，用来计算神经氨酸苷酶等生物大分子体系。Karplus小组［47］提出了AM1/CHARMM的组合方法思想，应用于DNA糖基化酶等生物大分子体系的计算研究。杨伟涛小组［48］研究了QM/MM组合方法中自由能和静电势的计算，QM与MM边界的处理等问题，并为组合方法的发展做出了重要的贡献。高加力和莫亦荣小组［49］建立了块定域波函数方法(BLW)和广义杂化轨道方法(GHO)，并把它们广泛应用于QM/MM组合方法计算。Thiel小组［50］发展了半经验方法，并利用MNDO/MM MD结合热力学积分的方法来计算反应自由能。张增辉［51-53］采用极化力场方法，研究了大量蛋白质分子的光谱性质。曹泽星［54-55］研究了磷酸葡萄糖异构酶和鼠李糖异构酶的催化机理，阐明了两种水解酶在Zn配位结构上的差异性。徐定国［56］研究了透明质酸酯裂解酶的催化反应，提出了顺式消除反应的机理。王永［57］研究了细胞色素P450蛋白酶活化C-H键的反应机理，结果表明电子转移在催化反应中起着重要的作用。马晶［58］、刘成卜［59-60］等采用QM/MM组合方法，在酶催化反应机理领域也做出了重要贡献。

3 结论

美国化学学会会长Marinda Li Wu称今年的诺贝尔奖“令人非常兴奋”。她解释道:“获奖者通过计算机模型，为经典实验科学与理论科学的联系奠定了基础。由此得到的见解正在帮助我们开发新的药物。比如，他们的成果正在用于决定药物如何与体内蛋白质相互作用，从而治疗疾病。”QM/MM组合方法的发展，并且在研究凝聚态中的化学反应和生物大分子尤其是酶催化反应的机理等方面有着广泛的应用，为处理庞大而又复杂的体系提供了一种强有力的工具。

［1］Field M J，Bash P A，Karplus M.J Comput Chem，1990，11:700

［2］Warshel A，Levitt M.J Mol Biol，1976，103:227

［3］Elsasser B，Fels G，Weare J H.J Am Chem Soc，2014，136:927

［4］Gotz A W，Clark M A，Walker R C.J Comput Chem，2014，35:95

［5］Pecina A，Lepsik M，Rezac J，et al.J Phys Chem B，2013，117:16096

［6］Thellamurege N M，Si D J，Cui F C，et al.J Comput Chem，2013，34:2816

［7］Nakayama A，Arai G，Yamazaki S，et al.J Chem Phys，2013，139:214304

［8］Golze D，Iannuzzi M，Nguyen M T，et al.J Chem Theory Comput，2013，9:5086

［9］Bakowies D，Thiel W.J Phys Chem，1996，100:10580

［10］Riccardi D，Schaefer P，Cui Q.J Phys Chem B，2005，109:17715

［11］Maseras F，Morokuma K.J Comput Chem，1995，16:1170

［12］Humbel S，Sieber S，Morokuma K.J Chem Phys，1996，105:1959

［13］Vreven T，Morokuma K.Theor Chem Acc，2003，109:125

［14］MacKerell A D Jr，Brooks B，Karplus M，et al.CHARMM:The Energy Function and Its Parameterization with an Overview of the Program∥von Rague Schleyer P.Encyclopedia of Computational Chemistry.Vol 1.Chichester:Wiley，1998:271

［15］http:∥www.charmm.org/

［16］Case D A，Cheatham T E，Darden T，et al.J Comput Chem，2005，26:1668

［17］http:∥amber.scripps.edu/

［18］Singh U C，Kollman P A.J Comput Chem，1986，7:718

［19］Bakowies D，Thiel W.J Phys Chem，1996，100:10580

［20］Murphy R B，Philipp D M，Friesner R A.J Comput Chem，2000，21:1442

［21］Riccardi D，Li G，Cui Q.J Phys Chem B，2004，108:6467

［22］Antes I，Thiel W.J Phys Chem A，1999，103:9290

［23］Zhang Y，Lee T S，Yang W.J Chem Phys，1999，110:46

［24］Zhang Y.J Chem Phys，2005，122:024114

［25］Alary F，Poteau R，Heully J L，et al.Theor Chem Acc，2000，104:174

［26］Assfeld X，Rivail J L.Chem Phys Lett，1996，263:100

［27］Philipp D M，Friesner R A.J Comput Chem，1999，20:1468

［28］Gao J，Amara P，Alhambra C，et al.J Phys Chem A，1998，102:4714

［29］Zwanzig R W.J Chem Phys，1954，22:1420

［30］Senn H M，Thiel S，Thiel W.J Chem Theory Comput，2005，1:494

［31］Torrie G M，Valleau J P.J Comput Phys，1977，23:187

［32］Bartels C，Karplus M J.J Comput Chem，1997，18:1450

［33］Bouzida D，Swendsen R H，Kollman P A，et al.J Comput Chem，1992，13:1011

［34］Scott W R P，Hünenberger P H，Tironi I G，et al.J Phys Chem A，1999，103:3596

［35］Jorgensen W L，Maxwell D S，Tirado-Rives J.J Am Chem Soc，1996，118:11225

［36］Jorgensen W L.OPLS Force Fields∥von RaguéSchleyer P.Encyclopedia of Computational Chemistry.Vol 3.Chichester:Wiley，1986:1998

［37］Kaminski G A，Friesner R A，Tirado-Rives J，et al.J Phys Chem B，2001，105:6474

［38］Lii J H，Allinger N L.J Am Chem Soc，1989，111:8566

［39］Lii J H，Allinger N L.J Comput Chem，1991，12:186

［40］Allinger N L，Chen K S，Lii J H.J Comput Chem，1996，17:642

［41］Langley C H，Lii J H，Allinger N L.J Comput Chem，2001，22:1396

［42］Halgren T A.J Comput Chem，1996，17:490

［43］Halgren T A.J Comput Chem，1996，17:520

［44］Rappe A K，Casewit C J，Colwell K S，et al.J Am Chem Soc，1992，114:10024

［45］Casewit C J，Colwell K S，Rappe A K.J Am Chem Soc，1992，114:10035

［46］Case D A，Seetin M G，Sagui C，et al.AMBER 10.University of California，San Francisco，2008

［47］Bash P A，Field M J，Davenport R C，et al.Biochemistry，1991，30:5826

［48］Hao H，Yang W T.Annu Rev Phys Chem，2008，59:573

［49］Mo Y R，Zhang Y，Gao J L.J Am Chem Soc，1999，121:5737

［50］Bakowies D，Thiel W.J Phys Chem，1996，100:10580

［51］Ji C G，Zhang J Z H.J Am Chem Soc，2011，133:17727

［52］Wang X W，He X，Zhang J Z H.J Phys Chem A，2013，117:6015

［53］Xu J，Zhang J Z H，Xiang Y.J Phys Chem A，2013，117:6373

［54］Wu R B，Xie H J，Cao Z X，et al.J Am Chem Soc，2008，130:7022

［55］Wu R B，Gong W J，Ting L，et al.J Phys Chem B，2012，117:1984

［56］Zheng M，Xu D G.J Phys Chem B，2013，117:10161

［57］Shaik S，Cohen S，Wang Y，et al.Chem Rev，2010，110:949

［58］Jiang N，Ma J.J Phys Chem B，2010，114:11241

［59］Wang J H，Hou Q Q，Dong L H，et al.J Mol Graph Model，2011，30:148

［60］Sheng X，Gao J，Liu Y J，et al.J Mol Graph Model，2013，44:17