相对活度在物理化学课程中的应用*

2015-02-13宁爱民

大学化学 2015年2期

宁爱民

(河南农业大学理学院河南郑州450002)

有关活度、化学势及标准状态的概念，在20世纪80～90年代曾进行过较多的讨论［1-4］。这些内容在大部分物理化学教材中均用了较多的篇幅进行介绍［5-8］，在本科化学专业的课程教学中一般也都占有较多的学时，但是学生普遍认为这些内容既抽象不易理解，又难于系统掌握。如果引入相对活度的概念［9-13］，将有助于学生对化学势表达式和标准状态的理解和应用，增强课程中一些内容和知识点的系统性，既有利于学生深刻理解和掌握相关知识，又可减少教材中一些不必要的重复推导和文字介绍，从而提高教学效率。

1 相对活度的概念

1.1 化学势表达式的通式

通常可以由两种方法得到化学势表达式的通式。

1)根据国家标准［14］和国际标准［15］以及有关文献［1］，任意系统中组分B的绝对活度λB的定义为:

式中μB(T，p)为组分B在一定温度T和压力p时的化学势，与T、p及组成有关，R为气体常数。组分B的标准绝对活度的定义［15］为:

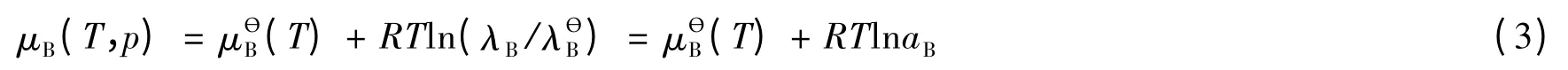
式中aB为组分B的相对活度。aB的定义式为:

相对活度的概念在一些国外的教材［9-12］中均有体现和应用，但在国内的教材中应用很少［13］。

2)分别对不同组分的化学势表达式进行推导，然后归纳为一个通式［13］:

式中FB对气体组分而言等于0;对非气体组分，有:

式中Vm，B为组分B在特定条件(不同系统中的组分，Vm，B的具体含义不同［2-3，13］)下的偏摩尔体积，pӨ为标准压力(105Pa)。FB是T和p的函数，与相对活度无关。对非气体组分，当p与pӨ相差不是很大时，FB值很小，通常可忽略［2-3，13］。这样，化学势表达式的通式就与式(3)相同了。

1.2 相对活度的定义

根据Mortimer R G编著的《Physical Chemistry》［9］，化学势表达式的通式用式(3)表示时，组分B相对活度的定义为“The activity is a dimensionless quantity that is equal to unity if the substance is in its standard state”(活度是物质在标准状态下等于1的无量纲的量)。对应的标准状态为:“温度为T，压力为pӨ，aB=1且活度系数γB=1的组分B”。若aB=1且γB=1的组分B并不真实存在，则标准状态为假想状态［2，4］。例如，对于非理想气体，aB=fB/pӨ=(γBpB)/pӨ(fB为逸度，γB为逸度系数或活度系数)，既要满足aB=1即fB=pӨ，又要满足γB=1即fB=pB，显然此状态对非理想气体并不存在，而是具有理想气体性质的假想状态［2，4］。这样，就可得到不同系统中组分相对活度的具体形式［9-12］及标准状态［2，4］，如表1所示。

表1 不同系统中组分的相对活度及标准状态

2 相对活度概念的应用

2.1 在平衡常数表达式及化学反应等温式中的应用

大部分物理化学教材在推导化学反应等温式及平衡常数表达式时，是将化学反应分为几种不同的类型(如理想气体反应，非理想气体反应，理想稀溶液反应，复相反应等)分别推导，这样既增加了教材中不必要的重复内容，也不利于学生系统掌握相关知识。在引入相对活度的概念后，根据化学势表达式的通式进行推导，可以克服这些弊端。

对于任意类型的化学反应(用通式aA+dD=gG+hH表示，简写为0=∑νBB，νB为B的化学计量系数，下同)，根据化学势表达式的通式(3)可推导得到化学反应等温式为［9-13］:

式中ΔrGm、Δr分别为化学反应的非标准和标准摩尔Gibbs自由能变，aB为反应系统中某反应物或产物的相对活度，Qa=∏B(aB)νB为反应的相对活度商。平衡常数KӨ表达式的通式为:

式中aeq，B为物质B平衡时的相对活度。从而，还可得到:

这样，只要把不同组分相对活度的具体形式代入式(7)～式(9)，就可得到任意类型化学反应的等温式和平衡常数表达式，包括弱酸和弱碱的电离常数、难溶电解质的溶度积常数、水的离子积常数以及分配定律表达式等。同时，由式(8)可以看出，KӨ与标准状态对应，仅是温度的函数。所以，其他的实验平衡常数(如Km、Kc、Kp、Kx、Kn等)都不遵守式(9)，均不能根据式(9)由ΔrGӨm直接计算。

2.2 在化学反应等压方程式中的应用

温度对化学反应平衡常数影响的等压方程式的定积分式可写为:

式中KӨ(T1)和KӨ(T2)分别为化学反应在温度T1和T2时的标准平衡常数，ΔHm为化学反应的摩尔焓变。该公式与溶液凝固点、沸点的计算公式以及温度对液体或固体饱和蒸气压影响的Clausius-Clapeyron公式的实质可以认为是一样的，它们之间的内在联系可通过平衡常数及相对活度的概念进行解释。

2.2.1 溶液凝固点的计算公式

KӨ(Tf)=1/aA。将和Tf两个温度时的KӨ代入式(10)即可得到稀溶液凝固点的计算公式为:

若为理想稀溶液，由于aA=xA，代入式(11)即可。若理想稀溶液中溶剂凝固时形成固溶体(固态混合物，用sln'表示，A的物质的量分数为xA')，即:

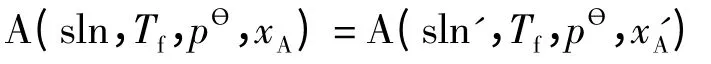
KӨ(Tf)=xA'/xA。代入式(10)即可。

2.2.2 溶液沸点的计算公式

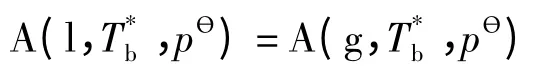
KӨ)=1，ΔHm=ΔvapHm(A)，ΔvapHm(A)为液体溶剂的摩尔蒸发焓。对于非挥发溶质形成的溶液，溶液中的溶剂在沸点Tb时蒸发为纯气体，溶液中溶剂与纯气体达到两相平衡，即:

KӨ(Tb)=1/aA。将和Tb两个温度时的KӨ代入式(10)即可得到溶液沸点的计算公式为:

若为理想稀溶液，由于aA=xA，代入式(12)即可。若是挥发性溶质形成的理想稀溶液，稀溶液中溶剂在沸点Tb时蒸发为混合气体中的气体溶剂，稀溶液中溶剂与混合气体中的气体溶剂(其物质的量分数为yA)达到两相平衡，即:

KӨ(Tb)=yA/xA。代入式(10)即可。

2.2.3 Clausius-Clapeyron公式

若纯液体(或固体)B在温度T1时的蒸气压为p1，纯液体(或固体)与纯气体(压力为p1)达到两相平衡，即:

KӨ(T1)=p1/pӨ，ΔHm为液体(或固体)的摩尔蒸发(或升华)焓。同理，若纯液体(或固体)在温度T2时的蒸气压为p2，则KӨ(T2)=p2/pӨ。代入式(10)即可得到Clausius-Clapeyron公式:

由前面的分析知，有了相对活度的概念和平衡常数表达式的通式后，式(10)～式(13)就具有一定的内在联系，只要有了式(10)，就可得到其他几个公式。

2.3 在稀溶液定律中的应用

根据相对活度的定义，稀溶液的拉乌尔定律和亨利定律可用如下通式表示:

式中pB为组分B在溶液液面上方气相中的分压，aB为该组分在溶液中的相对活度，ka为常数。对理想稀溶液中的溶剂A，ka为同温度下纯溶剂的饱和蒸气压，因此pA=xA，即拉乌尔定律。对理想稀溶液中的溶质B，ka为亨利系数。因理想稀溶液中溶质B的活度有mB/mӨ、cB/cӨ、xB3种形式，所以pB=km(mB/mӨ)=kc(cB/cӨ)=kxxB，即亨利定律。

稀溶液定律的公式用通式(14)表示后，具有以下几个优点:①对理想稀溶液和非理想稀溶液均成立;②对稀溶液中溶剂和溶质都适用;③亨利系数km、kc、kx的单位均统一为压力单位Pa;④在根据亨利定律推导理想稀溶液中溶质化学势表达式时，不需要人为地通过式子变换引入cӨ或mӨ的项［13］，避免了学生对一些公式推导产生的误解，有利于学生对标准状态的理解。

3 结语

综上所述，在引入相对活度的概念后，任意组分的化学势均可用一个通式来表示，组分标准状态的含义相对容易理解，热力学中一些重要知识的系统性更强，一些公式之间的内在联系更为清晰，同时还可减少相关知识点在物理化学教材中的简单重复，有利于学生深刻理解和系统掌握相关知识，对提高教师的授课效率和学生的学习效率均有一定的帮助。

［1］许海涵.化学通报，1987(4):51

［2］姚允斌.大学化学，1988，3(4):40

［3］刘晓地，童汝婷.化学通报，1991(5):40

［4］姚天扬.大学化学，1995，10(2):18

［5］韩德刚，高执棣，高盘良.物理化学.第2版.北京:高等教育出版社，2009

［6］傅献彩，沈文霞，姚天扬，等.物理化学(上册).第5版.北京:高等教育出版社，2005

［7］刘俊吉，周亚军，李松林.物理化学(上册).第5版.北京:高等教育出版社，2009

［8］胡英，吕瑞东，刘国杰，等.物理化学.第5版.北京:高等教育出版社，2007

［9］Mortimer R G.Physical Chemistry.3rd ed.New York:Elsevier Academic Press，2008

［10］Atkins P，Paula J.Physical Chemistry.8th ed.New York:W.H.Freeman＆Company，2006

［11］Ott J B，Boerio-Goates J.Chemical Thermodynamics:Principles and Applications.New York:Elsevier Academic Press，2000

［12］Kaufman M.Principles of Thermodynamics(Undergraduate Chemistry:A Series of Textbooks).New York:Marcel Dekker，2002