结构性软黏土损伤变量与扰动度的相关性研究
2015-02-13张彤炜徐海波邓永锋
张彤炜,徐海波,邓永锋
(东南大学 交通学院 岩土工程研究所,江苏 南京 210096)
1 引 言
地基土的工程施工、基坑的开挖等都会对结构性软黏土产生扰动,致使土体微观结构损伤和宏观强度衰减,给工程带来潜在危害。土体受到扰动,其相应的土体强度和压缩特性都会发生改变[1-2]。土体受到外界影响,发生性状改变的程度称为扰动度,国内外众多学者已经对土体扰动度展开了深入的研究。
Hvorslev[3]针对取样土体受扰动后孔隙水压力发生变化这一特征,定义扰动度为残余孔隙水压力与初始孔隙水压力的比值;徐永福等[4]为反映盾构施工对周围土体的应力扰动程度,采用土体的原位有效应力和受盾构掘进影响后土体的有效应力的比值来评价扰动度;Ladd等[5]认为,饱和土样的不排水模量受扰动的影响最为敏感,可以利用不排水模量的变化来评价土样受扰动的程度;Schmertmann[6]根据室内压缩试验的e-lgp 曲线,将原状土与完全扰动的重塑土样在屈服应力下的孔隙比差值与原状土和扰动土孔隙比的差值对比进行扰动评价;Nagaraj等[7]根据原状土、扰动土压缩曲线中屈服应力和回弹指数的变化给出土体扰动程度的评价方法;Hong等[8]则根据双对数坐标ln(1+e)-lgp 下取样扰动对土体压缩曲线的屈服前、后的斜率变化定义了扰动度;王军等[9]采用施打排水板前、后地基土的十字板剪切峰值强度比值来评价地基处理对土体施工扰动。
综上所述,扰动度是土体劣化状态及其对应工程参数的描述,而快速施工过程中更关注的是应力状态变化过程中土体参数的演化(如图1所示),为此需要明确扰动度随应力状态的演化规律。

图1 研究问题的来源Fig.1 Motivation of the research problem
为了将土体应力状态变化过程与土体扰动度建立关系,可引入土体损伤变量的概念。根据损伤力学定义,在外部因素(如力、温等)的作用下、材料内部将形成一定的微观缺陷,这些缺陷扩展、汇合将造成材料逐渐劣化甚至破坏。从本质上讲,这些缺陷是离散的,但作为一种简单的近似,在连续损伤力学中,所有的微缺陷被连续化,它们对材料的影响可用一个或几个连续的内部变量来表示,这种变量称为损伤变量。用损伤力学来描述土体在外力作用下破损过程的关键问题是寻找一个或多个能够反映土体破损规律的损伤变量,并建立其演化方程。
沈珠江[10]在弹塑性及非线性损伤模型中采用的损伤演化函数为基于体应变和剪应变的指数或双曲线函数;胡黎明等[11]在应变软化和剪胀现象的粗糙接触面问题中,假定损伤状态变量为接触面塑性剪切应变的函数。损伤变量与土体应变结合,借助应变的变化来反推损伤的变化,损伤变量函数比较复杂,一旦其中某个参数发生变化,得到的结果可能与实际工程相差较大。
Desai等[12]1986年提出扰动状态概念(DSC),其扰动因子可表示为由应力-应变历史、初始密度、初始压力、颗粒间接触面性质、温度和时间的参数。张孟喜[13]考虑了施工扰动对土体应力状态、应力路径和孔隙比的影响,认为土体受到扰动后,会沿着扰动应力路径和孔隙比变化路径到达破坏曲面。根据p-q-e 空间中类似于土体的破坏面,提出一种损伤变量的表达式为

式中:ΔF为由施工扰动引起的应力路径平均应力、偏应力和孔隙比变化的矢量和;F为按照潜在的应力路径及孔隙比的变化方式计算的从初始状态到破坏曲面的3个变量的矢量和;Δp、Δq 和Δe分别为扰动引起的平均应力增量、偏应力增量和孔隙比增量;pf、qf和 ef为从初始状态到破坏曲面的球应力增量、偏应力增量和孔隙比增量。饱和软土在不排水状态下,孔隙体积不发生明显改变(即e变化很小),在分析中该项影响较小。此后,卫振海等[14]通过建立颗粒结构模型对颗粒系统的强度问题进行了分析。熊春发等[15]以天津海积软黏土为研究对象,对原状土及重塑土进行了不同固结压力、应力路径、加荷速率、排水条件下的三轴剪切试验,以应力比结构性参数与应变的关系来描述结构性衰减,研究了不同加荷模式下的结构损伤特性。
基于以往研究,本文采用不同的应力加载路径制样,将平均应力和偏应力作为变量简化损伤变量表达式,然后对试样分别进行常规固结试验和无侧限抗压强度试验,用不同方法描述扰动度,探究劣化状态的扰动度和表示劣化过程的损伤变量的关系。
2 试验材料及方法
2.1 试验材料
试验土样取自江苏省临海高等级公路,属于典型的连云港海相软土。为了减少取样过程中扰动对土体的影响,采用薄壁取土器静压取样,取土器直径为30 cm。取样时先挖除表层土,再人工挖除上部土体,然后把直径30 cm的静压桶垂直匀速压入土中,人工挖除静压桶周围土体。
将取回的部分土样自然风干,碾碎后过0.5 mm直径的标准筛,通过蝶式仪测定液限,采用搓条法测定塑限,采用比重瓶法测定比重,具体操作参照土工试验方法标准[16]。获得的基本物理指标列于表1,同时根据指标绘制塑性图,如图2所示。从塑性图可以看出,连云港软土属于高液限黏土(CH)。图中CL代表低液限黏土,MH代表高液限粉土,ML代表低液限粉土,O代表含有机质。

表1 土样的主要物理指标Table 1 Physical properties of samples
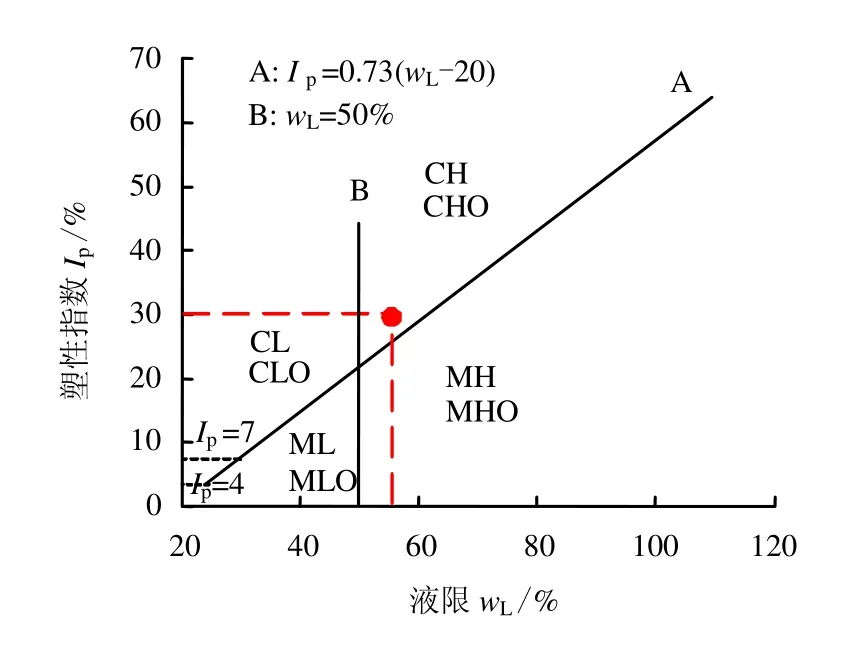
图2 连云港软土塑性图Fig.2 Plasticity chart of Lianyungang soft soil
2.2 试验方法
(1)三轴试验试样制备
将现场采集的土样用多层保鲜膜包裹并蜡封,放入养护室中储存。试验时,用钢丝锯和切土器制备直径100 mm,高度100 mm的土样。试验切削时尽量避免扰动,并取余土测定试样含水率。将所制得土样放入饱和器中进行抽真空饱和。
(2)三向等压固结试验
为了使土样达到一个同一均匀的初始状态,对土样施加一个大于先期固结压力和结构屈服应力的有效固结压力,本次试验根据土样埋深取有效固结压力为60 kPa。采用改进后GDS三轴试验系统。试验过程中先施加有效压力10 kPa进行反压饱和(围压为100 kPa,反压为90 kPa),然后进行孔隙水压力系数B 值测定,当B>0.95时,认为土样达到饱和。饱和完成后,施加60 kPa有效固结压力(围压为150 kPa,反压为90 kPa)进行固结。当孔隙水压力基本消散完毕和反压排水体积趋于恒定时,认为固结完成,以此作为初始应力状态。
(3)不同损伤程度试样制备
当三向等压固结试验完成后,认为土样达到同一状态,此时再对试样土体快速施加不同的偏应力,模拟不同的应力状态改变对土体的扰动。

表2 不同的应力路径列表Table 2 List of stress paths
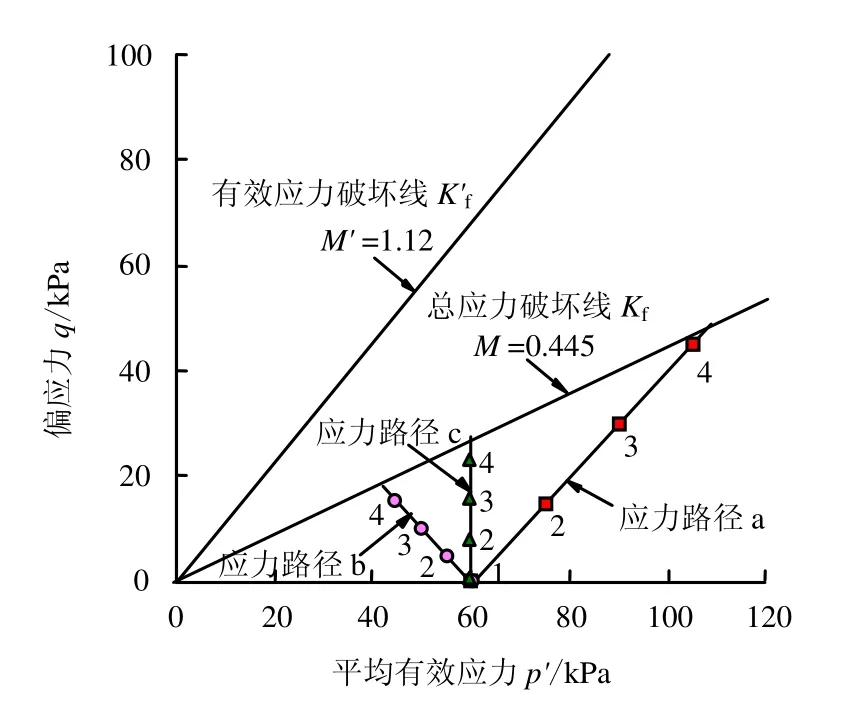
图3 应力加载路径示意图Fig.3 Schematic diagram of stress paths
制样之前先根据三轴抗剪强度试验作总应力圆和有效应力圆,得出土的固结不排水剪切试验(CU)的内摩擦角 φCU为12.0°,固结排水剪切试验(CD)的内摩擦角 φCD为28.3°。剑桥模型的破坏准则为q=Mp,其中M为破坏线的斜率,p=(σa+2σr)/3为三轴试验中平均应力,σa和σr分别为有效轴压与围压;q=(σa-σr)为三轴试验的偏应力。

根据式(2)得出有效应力破坏线斜率M′=1.12,总应力破坏线斜率 M=0.445。将总应力破坏线Kf作为控制线,在应力路径a、b、c选取应力状态点,通过GDS三轴仪中的应力路径系统进行快速加载,试验过程中关闭反压阀门。控制应力加载路径如图3所示,图中的1~4点为每一路径上的应力状态点,具体值列于表2,制作的损伤试样标号a-1代表应力路径a上的应力状态点1。
(4)常规固结试验
通过三轴试验装置施加不同的轴压与围压后,迅速释放三轴压力室中的压力,采用环刀法制备直径为61.8 mm,高度为20 mm的试样.固结试验中,预压1 kPa的荷载,然后进行加荷比为1的分级加载压缩试验,加载范围为12.5~1 600 kPa,记录固结过程中竖向变形,固结稳定的标准是变形量小于0.01 mm/h。
(5)无侧限抗压强度试验
紧接试验步骤(4),取同一批施加不同轴压与围压的试样,置于切土器中用钢丝锯切割土样,土样直径为38 mm,高度统一取70 mm。试样制备完成后放置于应变控制式无侧限抗压强度仪中,以轴向应变1%/min控制速度,传感器记录试验过程应力、应变读数。以最大轴向应力作为无侧限抗压强度,若最大轴向应力不明显,取轴向应变15%处的应力作为该试样的无侧限抗压强度。
3 试验结果与分析
3.1 扰动度
3.1.1 以变形定义的扰动度
Butterfield[17]通过对大量的固结试验数据进行分析,采用比容(v=1+e)和固结压力p 的双对数坐标描述固结压缩曲线。Hong等[8]根据Butterfield的研究,采用Butterfield体系改进了传统的体积压缩法,得到扰动度的定义为


图4 修正体积压缩法扰动度定义Fig.4 Definition of the disturbance degree using the revised volumetric compression method
式中:CCLB、CCLR分别为ln(1+e)-lgp 坐标下,土体扰动样和重塑样的压缩曲线屈服前的斜率如图4所示。Hong等[8]还通过研究发现,CCLR为液限的函数,即CCLR=-0.39+0.332lgwL。图5为不同应力状态下对扰动试样进行常规固结试验所得的土体的ln(1+e)-lgp 曲线。本文参照了式(3)对土体扰动度的描述,以变形定义的扰动度SDd描述不同应力路径下土体的压缩特性。根据图4,分别计算不同扰动试样在ln(1+e)-lgp 坐标下屈服应力前的斜率CCLB,将液限wL=57.6%代入Hong等建立的公式CCLR=-0.39+0.332lgwL,得到重塑样的压缩曲线斜率CCLR,带入式(3)后得到试样以变形定义的扰动度SDd,结果如表3所示。

图5 不同应力路径的ln(1+e)-lgp 曲线Fig.5 ln(1+e)-lgp curves for different stress paths

表3 扰动度SDdTable 3 Disturbance degree SDd
3.1.2 以强度定义的扰动度
王军等[9]以十字板剪切试验测定的不排水强度为特征量来定量评价地基处理的扰动程度,定义扰动度为

式中:Su、分别为施打排水板前、后的地基十字板剪切峰值强度。
无侧限抗压强度试验获得的qu与饱和黏性土的不排水抗剪强度的Cu关系为qu=2Cu,因此,可采用无侧限抗压强度的损失值来描述扰动度,本文以强度定义的扰动度SDs计算公式为

式中:qu为初始应力状态点无侧限抗压强度;qu′为土体从初始应力状态点到应力路径某一点后的无侧限抗压强度。无侧限抗压强度试验结果如图6所示,取轴向应变15%处的应力作为该试样的无侧限抗压强度。由于所有试样的有效固结压力为60 kPa,因此,将p′=60 kPa,q=0下制备的试样作为初始应力状态点,其无侧限抗压强度为式(5)中的qu,根据公式(5)计算扰动度SsD 列于表4。
3.2 描述应力状态的损伤变量
损伤变量为影响材料本构关系的内部变量。本文为了将结构性软黏土加载的某一应力状态与土体的扰动程度建立联系,引用损伤变量的概念。张孟喜[13]考虑了施工扰动对土体应力状态、应力路径和孔隙比的影响,将损伤变量在三维坐标中进行定义,如式(1)所示。这种方法既考虑了土体受力状态的改变,又考虑了土体主要物理参数的改变。而实际应用中,如果只考虑施工造成的土体应力状态的变化,可以在二维坐标系中简化损伤变量的定义,将平均应力和偏应力作为变量,最终简化损伤变量的表达式为
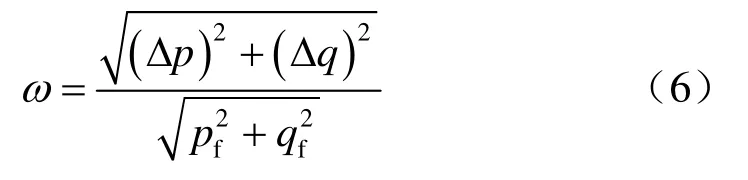
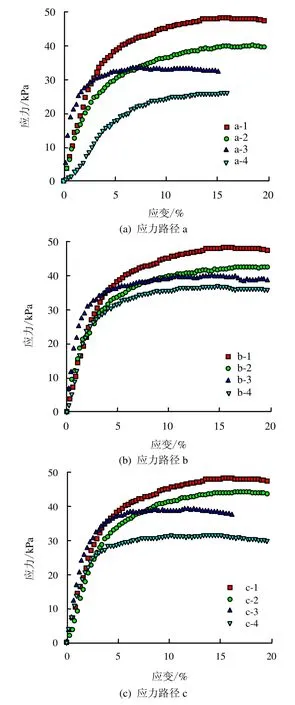
图6 不同应力路径的无侧限抗压强度试验结果Fig.6 Unconfined compressive strength testing results for different stress paths

表4 扰动度SDsTable 4 Disturbance degree SDs
式中:Δp、Δq 分别为扰动引起的平均应力增量和偏应力增量;pf和qf为从初始状态沿着某一应力路径到破坏线的平均应力和偏应力。a-1、b-1、c-1都为初始应力状态,所以Δp、Δq为0。计算不同的应力路径a、b、c下的ω 值,分别采用p-q 坐标下Kf与a、b、c的交点作为相应的pf和qf,如图3所示。根据式(6)计算所得损伤变量列于表5。需要强调的是,本文对损伤变量的定义,只用于描述土体应力状态改变。

表5 不同的应力路径的损伤变量Table 5 Damage variable of different stress paths
3.3 扰动度与描述应力状态的损伤变量关系的探讨
沈珠江等[18]认为,天然结构性土体的劣化过程,是从原状土向扰动土变化的过程,是其原生结构逐渐破坏,而次生结构逐渐产生的过程,这就意味着代表扰动过程的损伤变量和代表应力状态的扰动度可以建立关系。
结合上述试验结果,可以分别建立描述应力状态的损伤变量与以变形定义的扰动度SDd和以强度定义的扰动度SDs的关系,结果如图6、7所示。
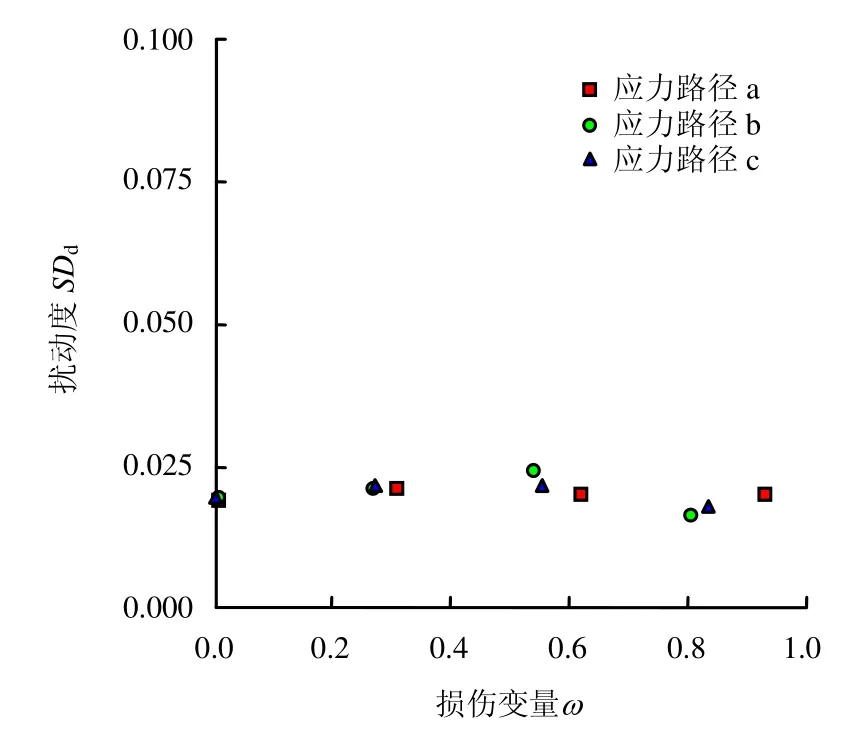
图7 损伤变量与扰动度SDd的对应关系Fig.7 Relationship between damage variable and disturbance degree SDd

图8 损伤变量与扰动度SDs的对应关系Fig.8 Relationship between damage variable and disturbance degree SDs
从结果可知,以变形定义的扰动度SDd,并未随着损伤变量的增加而产生明显的变化。这说明,不同的应力路径,对ln(1+e)-lgp 坐标下土体扰动样和重塑样的压缩曲线屈服前的斜率比值并未产生明显影响,因此,用土体体积的变化反映不同应力路径下土体损伤的程度并不容易。损伤变量与以强度定义的扰动度SDs具有很好的线性相关性,线性拟合公式为ω=0.41SDs,R2=0.95。这说明当土体沿着某一路径加载,越接近破坏线,其损伤程度越高,土体的强度也随之降低。
4 结 论
(1)通过在三轴试验仪中对土体施加不同的p、q 来制取不同损伤程度试样。根据本研究特点,优化了张孟喜等提出的损伤变量的表征方法。
(2)对不同损伤程度土体进行常规固结试验,参照Hong等关于取样土体扰动度的描述,采用以变形定义的扰动度SDd建立与损伤变量之间的关系,发现不同应力路径下的SDd并未随着损伤变量的增加而产生明显的变化。
(3)对不同损伤程度的土体进行无侧限抗压强度试验,采用无侧限抗压强度损失值SDs来描述扰动度,通过SDs与损伤变量的对应关系发现二者具有很好的相关性,即当土体沿着某一路径加载,越接近破坏线,其扰动程度越高,土体的强度也随之降低。
[1]杨守华,魏汝龙.土样扰动对正常固结粘土强度及压缩特性的影响[J].水利水运科学研究,1992,(1):73-83.YANG Shou-hua,WEI Ru-long.Influence of sampling disturbances on strength and consolidation behavior of normally consolidated clay[J].Hydro-Science and Engineering,1992,(1):73-83.
[2]邓永锋,刘松玉.扰动对软土强度影响规律研究[J].岩石力学与工程学报,2007,26(9):1940-1944.DENG Yong-feng,LIU Song-yu.Effect of sample disturbance on soft soil strength[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(9):1940-1944.
[3]HVORSLEV M J.Subsurface exploration and sampling of soils for civil engineering purposes[M].[S.l.]:ASCE,1949.
[4]徐永福,陈建山,傅德明.盾构掘进对周围土体力学性质的影响[J].岩石力学与工程学报,2003,22(7):1174-1179.XU Yong-fu,CHEN Jian-shan,FU De-ming.Effect of shield tunneling on mechanical properties of soils[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(7):1174-1179.
[5]LADD C C,LAMBE T W.The strength of "undisturbed"clay determined from undrained tests[M].[S.l.]:Department of Civil Engineering,Massachusetts Institute of Technology,1963.
[6]SCHMERTMANN J H.Estimating the true consolidation behavior of clay from laboratory test results[C]//Proceedings of ASCE.[S.l.]:[s.n.],1953,79(311):26.
[7]NAGARAJ T S,MURTHY B R S,VASTALA A,et al.Analysis of compressibility of sensitive soils[J].Journal of Geotechnical Engineering,ASCE,1990,116(1):105-118.
[8]HONG Z,ONITSUKA K.A method of correcting yield stress and compression index of Ariake clays for sample disturbance[J].Soils and Foundations,1998,38:211-222.
[9]王军,高玉峰,高红珍.结构性软土地基施工扰动定量分析[J].岩土力学,2005,26(5):789-794.WANG Jun,GAO Yu-feng,GAO Hong-zhen.Quantitative analysis of foundation treatment disturbance of structured soft clay ground[J].Rock and Soil Mechanics,2005,26(5):789-794.
[10]沈珠江.结构性粘土的弹塑性损伤模型[J].岩土工程学报,1993,15(3):21-28.SHEN Zhu-jiang.An elasto-plastic damage model for cemented clays[J].Chinese Journal of Geotechnical Engineering,1993,15(3):21-28.
[11]胡黎明,濮家骝.土与结构物接触面损伤本构模型[J].岩土力学,2002,23(1):6-11.HU Li-ming,PU Jia-liu.Damage model of soil-structure interface[J].Rock and Soil Mechanics,2002,23(1):6-11.
[12]DESAI C S,TOTH J.Disturbed state constitutive modeling based on stress-strain and nondestructive behavior[J].International Journal of Solids and Structures,1996,33(11):1619-1650.
[13]张孟喜.受施工扰动土体的工程性质研究[D].上海:同济大学,1999.
[14]卫振海,王梦恕,张顶立.土结构强度模型研究[J].岩土力学,2013,34(1) :41-46.WEI Zhen-hai,WANG Meng-shu,ZHANG Ding-li.Study of strength model of soil structure[J].Rock and Soil Mechanics,2013,34(1):41-46.
[15]熊春发,孔令伟,杨爱武.加荷模式对海积软黏土结构损伤性状的影响分析[J].岩土力学,2014,35(7):1893-1898.XIONG Chun-fa,KONG Ling-wei,YANG Ai-wu.Analysis of influence of loading mode on character of structural damage of marine soft clay[J].Rock and Soil Mechanics,2014,35(7) :1893-1898.
[16]中华人民共和国水利部.GB/T50123-1999土工试验方法标准[S].北京:中国计划出版社,1999.
[17]BUTTERFIELD R.A natural compression law for soils(an advance on e-lgp')[J].Geotechnique,1979,29(4):469-480
[18]沈珠江,章为民.损伤力学在土力学中的应用[C]//第三届全国岩土力学数值分析及解析方法讨论会论文集.武汉:武汉测绘科技大学出版社,1988.
