降雨条件下浅层滑坡稳定性探讨
2015-02-13常金源伍法权常中华
常金源,包 含,伍法权,常中华,罗 浩
(1.绍兴文理学院 土木工程学院,浙江 绍兴 312000;2.中国科学院地质与地球物理研究所,北京 100029;3.中国科学院大学,北京 100049;4中国地震局地质研究所 活动构造与火山重点实验室,北京 100029;)
1 引言
降雨条件下,特别是大雨或暴雨诱发下的浅层滑坡是一种常见、多发的地质灾害现象[1],如热带和亚热带地区(香港地区[2])的残积土滑坡,我国南方以及中南、西南部分地区山地或人工边坡[3-4]等。其分布范围广泛,危害性大,每年都会造成严重的生命财产损失,因此,开展对此类边坡的研究具有重要的现实意义。
这种地质灾害现象与降雨过程有着密切的联系。降雨入渗使得边坡的安全系数降低,主要表现在[5]:一方面增加了边坡体的自重,使得下滑力增加;另一方面,随着含水率的增高,土体的强度指标(内摩擦角φ 和黏聚力c)随之下降,而且在饱水的条件下降到最低点,使得边坡体的抗滑力大为降低。同时,边坡体内的水力渗流所产生的动水压力,也将使得边坡体下滑力增加,稳定性降低。
浅层滑坡由于滑坡的深长比小,一般都将其作为无限平面滑动型滑坡来研究。Skempton等[6]建立了平行与坡表入渗条件下的无限边坡模型,并求取了边坡的安全系数表达式;Pradel等[7]以南加利福尼亚为研究区,研究了均质边坡在长历时、高强度降雨条件下发生的浅层滑坡现象,提出无限平面滑动型边坡模型;Sung等[8]以Mein和Larson入渗模型[9]为基础,对Pradel等提出的方法进行了改进,考虑了坡表积水前的入渗情况;兰恒星等[10]指出,香港的降雨滑坡以浅层的风化残积层和堆积层为主,滑动类型一般为小型的平面或非圆弧滑动;许建聪等[11]利用数值模拟的方法分析了强降雨作用下的浅层滑坡稳定性,结果显示,边坡破坏的形式基本上与坡表是平行的。但这些研究并没有考虑边坡渗流中动水压力的作用,以及存在地下水位的情况。
Green-Ampt入渗模型[12]的假设条件是入渗边界为水平面,针对入渗边界与水平面呈一定角度的情况,即降雨条件下边坡的入渗情况,Philip[13]和Li等[14]进行了有益的研究探讨,扩展了Green-Ampt入渗模型的应用范围;顾成壮等[15]对强降雨诱发下的四川汉源二蛮山滑坡进行了研究,分析了强降雨饱和状态下平面滑动型(平滑型)滑坡的地下渗流的水流运动规律,并提出了饱和状态下此类滑坡的稳定性分析方法;何玉琼等[16]运用降雨阈值模型计算边坡单元变形失稳所需临界降雨量,分析降雨入渗以及地形坡度对边坡稳定性的影响。
本文以Green-Ampt入渗模型为基础,建立了降雨入渗条件下浅层滑坡的概念模型,并考虑动水压力的作用,分别探讨了有、无地下水位条件下的边坡安全系数与降雨时间的关系。以上研究均为本文提供了有益的参考。
2 Green-Ampt模型及其入渗分析
Green-Ampt模型研究的是初始干燥的土壤在薄层积水时的入渗问题,模型形式上较为简单,各参数具有明确的物理意义,便于建立特征参数与土壤物理特征间的联系。其计算结果也很精确,因此,得到了国内外学者的认同。该模型假设入渗条件下存在明显的湿润锋面,将湿润的和未湿润的区域截然分开,即在剖面上含水率的分布具有阶梯状特点,故也被称为活塞(或打气筒)模型[17]。其表达式为

式中:i为表面入渗率(m/s);Ks为饱和渗透系数(m/s);zf为湿润锋深度(m);sf为湿润锋处的土壤水吸力(为统一单位,此处单位用m,可以理解为某一高度水柱所产生的水压力);H为地表的积水深度(m)。
式(1)为地表水平假设条件下的Green-Ampt模型,对于边坡而言,由于入渗界面与水平面有一定夹角,模型需要相应地修正。Li等[14]根据边坡降雨入渗的特点,将式(1)修正为
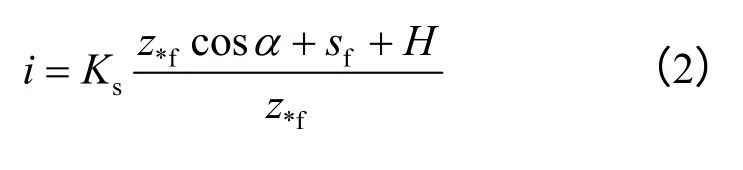
式中:z*f为垂直于边坡面的入渗深度(m);α为边坡面与水平面的夹角(°)。
将 z*f变换为竖直向入渗深度,由于 z*f=,则式(2)可表示为
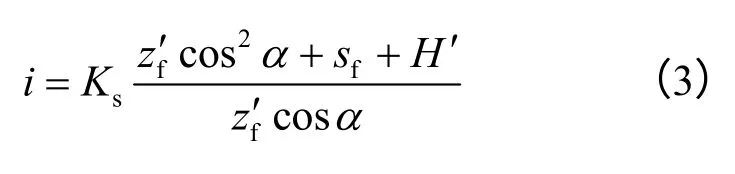
入渗量I(m3,单位宽度为1)可由水量平衡求得,即
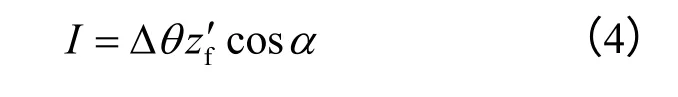
式中: Δθ为饱和、初始体积含水率之差。
而入渗率与入渗量的关系可表示为

联立式(3)和式(5)可得


积分上式,注意 t=0时 zf′=0,则有 zf′ -t 的关系式为
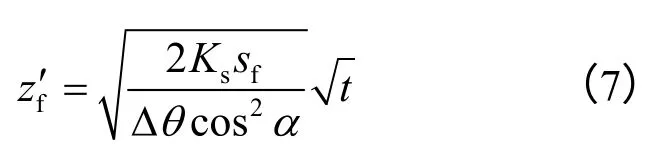
3 浅层滑坡稳定性分析
由于浅层滑坡往往深长比小,一般都将其作为无限平面滑动型滑坡来研究[6-10]。一次降雨过程对其稳定性的影响主要集中在降雨入渗量和入渗深度上。短历时、低强度的降雨往往仅使滑坡表层岩土体含水率增加,对整个滑坡稳定性影响非常有限;而长历时、高强度的降雨往往对滑坡稳定性产生很大影响,使得滑坡体在短时间内达到饱和状态,滑坡稳定性迅速降低[19]。下面将探讨此种情况下浅层滑坡稳定性与降雨历时之间的关系。
3.1 无地下水位条件下
3.1.1 假设条件(如图1所示)
(1)均质等厚土质坡体;(2)降雨强度大于坡体入渗率,坡体表层处于饱和状态;(3)滑坡沿滑带滑动。

图1 无地下水位条件下的模型示意图Fig.1 Model without groundwater
3.1.2 稳定性分析
取水平单位宽度坡体ΔL=1(m)进行分析,设h为边坡竖直向高度(m),h′为湿润锋竖直向入渗高度(m),α为坡角(°);γ为天然重度(kN/m3),γsat为饱和重度(kN/m3),γw为水的重度(kN/m3),Δγ=γsat-γ;φ为土体内摩擦角(°),c为土体黏聚力(kPa)。则单位宽度坡体重量为
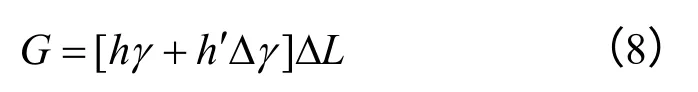
法向应力为

下滑力为

抗滑力为

渗透力为
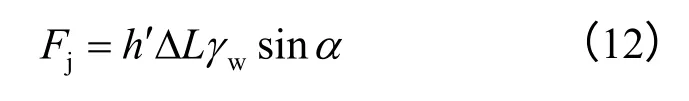
则由以上各式可得边坡的安全系数为
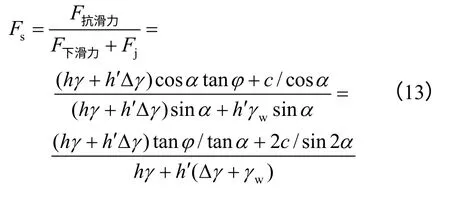
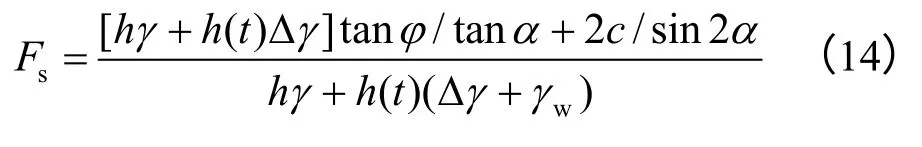
此式表示干燥边坡安全系数对于降雨入渗的响应。
假设在时刻t=tc时,湿润锋推进到滑带,滑带处于饱和状态,此时应取饱和条件下的有效内摩擦角φ′和有效黏聚力c′,则边坡的安全系数表达式为

由式(14)和式(15)可以得到边坡的安全系数表达式,如式(16)所示。表达式中Fs的值发生突变的主要原因归结于滑面在浸水饱和情况下,岩土体的强度迅速降低。

3.2 有地下水位条件下
3.2.1 假设条件(如图2所示)
(1)均质等厚土质坡体;
(2)降雨强度大于坡体入渗率,坡体表层处于饱和状态;
(3)滑坡沿滑带滑动;
(4)地下水位与滑带平行。
3.2.2 稳定性分析
取水平长度为ΔL=1(m)的坡体作为研究对象,其底部正应力为

图2 有地下水位条件下的模型示意图Fig.2 Model with groundwater

作用于滑面上的孔隙水压力[20]为

作用于滑面上的有效正应力为

滑带的抗剪强度为

则总抗滑力为

坡体下滑力为

则坡体安全系数为
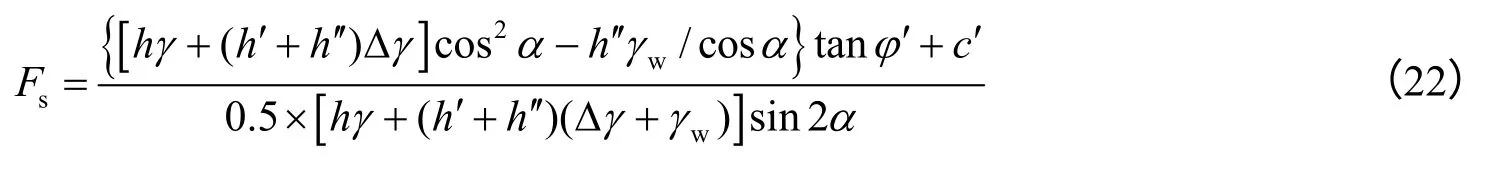
当湿润锋与地下水位线接触时,即h′+h ′=h 或t=(h-h′)2Δθcos2α/(2Kssf),滑面处的孔隙水压力会发生突变,将由原来的h ′γw/cosα 变为hγw/cosα 。孔隙水压力的突变也会造成滑面处有效应力的突变(减小),使得安全系数产生突降。由此得此种情况下的安全系数表达式为
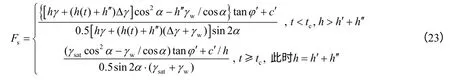
下面讨论湿润锋和地下水位接触时的情况。接触前的很短一段时间,h′+h ′≈ h,可以认为坡体饱和。此时滑面处的孔隙水压力为h ′γw/cosα,安全系数为
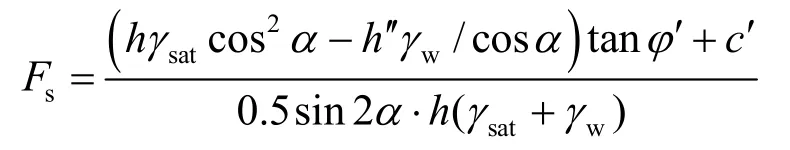
在湿润锋与地下水位接触的很短时间内,滑面处的孔隙水压力将发生迅速变化,由h ′γw/cosα→hγw/cosα,增加值Δ u=h ′γw/cosα 。此时由于孔隙水压力的增大使得安全系数降低值为

这可能就是降雨过程中或者降雨结束一定时间后浅层滑坡发生突然启动的内在原因。
3.3 试验验证
林鸿州[21]曾进行过降雨滑坡的模型试验(如图3所示),模型材料为粉细砂,材料参数如下:Ks=3.32×10-5m/s, Δθ=0.40,Gs=2.7,干密度dρ=1 500 kg/m3,γsat=19.4 kN/m3。模型参数如下:坡角α=33.7°,坡体的垂直厚度为0.5 m,4、6号张力计到坡面的垂直高度分别约为0.4、0.2 m,人工降雨强度为80 mm/h,大于Ks。
由图4可知,位于表层的1、3、6号张力计在一定时间内孔隙水压力读数保持在一个恒定的值,认为此时张力计周围土体已经饱和,即湿润锋已经通过张力计(之所以不等于0,是由于粉细砂中的一些小孔隙中仍有少量空气存在,难以排除)。由此可知,大约25 min时6号张力计周围土体饱和,大约72 min时4号张力计周围土体饱和,运用式(7)分别计算湿润锋此时的深度约为0.25 m和0.46 m,与张力计埋设深度接近。
由图4可知,在约83 min时,3号和4号张力计的读数有一个迅速增大的过程,随后渐趋平稳。认为此时滑带附近产生了剪切位移,形成超静水压所致。此时,根据提供的粉细砂土-水特征试验数据[22],通过内插可以得到当基质吸力为-3 kPa时,粉细砂的c′=3.2 kPa,φ′=34.3°。根据式(15)可以计算Fs为0.722。通过计算此时湿润锋的位置约为0.49 m,与坡体垂直厚度几乎一致。由此认为,Green-Ampt入渗模型和安全系数公式的应用是适用的。紧接着在90 min 52 s时,模型的坡脚开始出现挤出破坏现象。最终,试验确定的模型破坏时间为90 min 52 s。
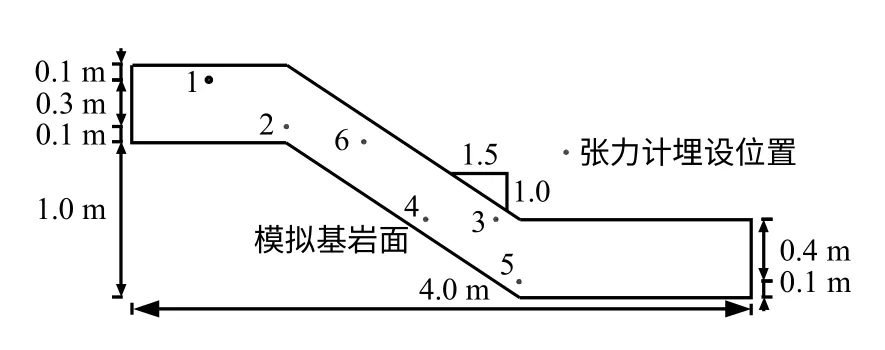
图3 张力计布置图[21]Fig.3 Locations of tensiometers
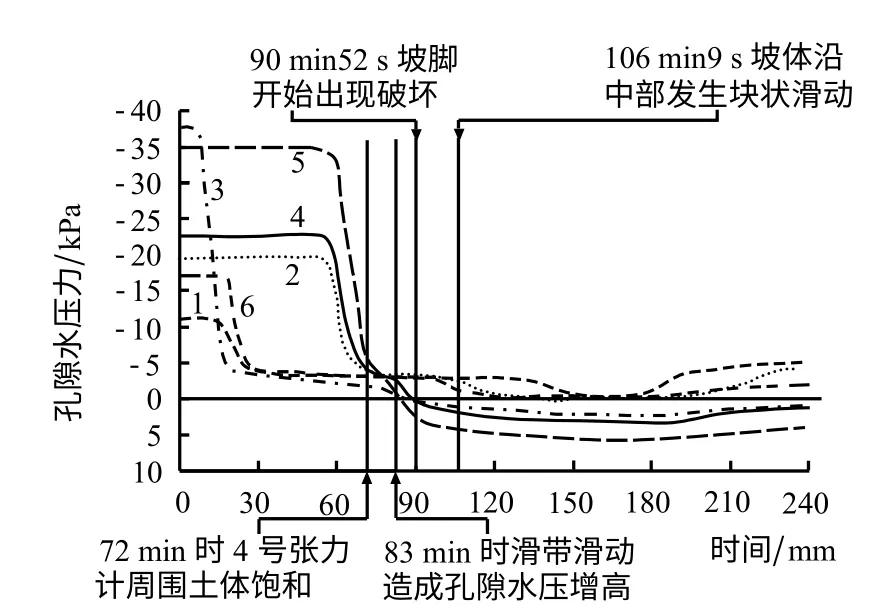
图4 张力计结果图[21]Fig.4 Result diagram of measurements
4 饱和临界时间
降雨初期,表面坡体基质吸力较大,入渗能力强,一般而言大于降雨强度,难以形成坡表径流。这一阶段称为通量控制阶段,属于无压入渗或自由入渗。随着降雨时间的增长,坡面土体逐渐饱和,在坡体内部也形成不断扩大的饱和区,含水率梯度不断减小,土壤入渗能力渐趋减弱,当土壤的入渗能力小于降雨强度时,将在坡表形成径流或积水。此阶段称为剖面控制阶段,为有压入渗。结合式(4)和式(7)可知:
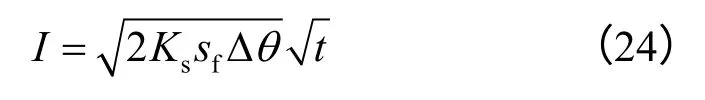
当降雨强度小于入渗率i 时,入渗量I 只取决于降雨强度的大小;而当降雨强度大于入渗率i 时,入渗量I 则与土壤的饱和渗透系数、基质吸力、饱和体积含水率和初始体积含水率的差值有着密切的联系。
由以上分析,可假设这样一种情况:对于一次强度(雨量)较大的降雨,整个降雨过程不仅使得坡体完全饱和,滑面或者潜在滑面也由于饱水抗剪强度降至最低值,坡体处于最不稳定状态,此时入渗量I 不再增加(实际情况应当为单位时间入渗量与坡体渗流排泄量相等,此时可认为降雨对坡体饱和程度没有贡献)。设降雨持续时间为t,降雨强度为R,降雨过程入渗量为I,使坡体完全饱和的临界降雨持续时间为 tc。如果降雨过程结束前坡体处于完全饱和状态,即湿润锋面与滑面或地下水位面相接触,此时,tc≤ t,I=Δθz′cosα,z '为非饱和带高度;如果降雨过程结束,湿润锋面与滑面或地下水位面没有接触,tc> t,I<Δθz′cosα。
对于 tc,可以这样求得:取边坡内一单位柱体,竖直厚度为z′,顶面为坡面,底面为地下水位面或潜在滑动面,如图5所示。

图5 降雨入渗模型Fig.5 Model of rainfall infiltration
设一次降雨过程使得单位宽度柱体刚刚饱和,此时的降雨持时即为 tc。柱体由非饱和到饱和转变过程中增加的水量为
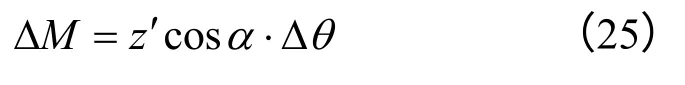
设想当降雨持时达到 tp时,i=R,此时即开始积水,则坡体表层饱和深度z′可由式(3)求得(认为H′≈0 m)

此时的累积入渗量为

降雨持时为
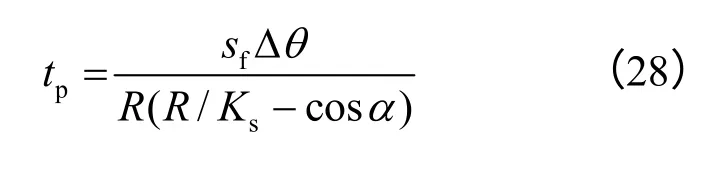
此时可将 tc分解为两个时间段,即为坡表积水后的降雨经历的时间。为求得 tp′,设想初始时间为0时即为饱和坡表入渗,则累计入渗量 I *为
式中:t *包含两个时间段,一个是使z′′饱和的时间t′′,剩下的为使(z ′ -z′′)饱和的时间,即。前者可以根据式(7)求得,于是:
将式(28)与式(30)相加即可得饱和临界时间为
对于暴雨而言,由于降雨强度大,在开始的很短时间内坡体表面即饱和,此时可以根据式(7)大概估计tc≈Δθ(z′cosα)2/(2Kssf)。
对于某一边坡,如果降雨持时小于 tc,则在整个降雨过程中坡体无法完全饱和;如果降雨持时大于 tc,则在降雨过程结束前,坡体将达到完全饱和,而在 tc以后,稳定系数一直处于最低点,这对边坡的稳定性极为不利,外部稍有扰动或岩土体自身强度降低到临界值即有发生滑坡的危险。
那么,根据在一次降雨过程中边坡是否会达到饱和可以将边坡划分为强渗型和弱渗型两种类型,对于强渗型边坡而言,单位时间内湿润锋入渗深度较大,往往一次较大强度(雨量)的降雨可以使边坡岩土体发生饱和,使得在降雨过程结束前边坡一直处于相对危险的状态;而对于弱渗型边坡,单位时间内湿润锋入渗深度较小,降雨过程结束后坡体仅发生部分饱和,此时坡体容易发生浅层破坏,即在坡体饱和部分发生剪切变形破坏,或者随着湿润锋的入渗,发生滞后于降雨过程的破坏。
5 结论
(1)对于没有地下水位的边坡而言,当湿润锋到达滑带位置时,安全系数将会发生突变,主要原因归结于滑带在浸水饱和情况下,土体的抗剪强度指标迅速降低。
(2)对于有地下水位的边坡而言,在湿润锋与地下水位面接触的很短时间内,滑面处的孔隙水压力将发生迅速变化,变化大小与湿润锋的运移高度呈正比;由于孔隙水压力的增大使得安全系数迅速降低,这可能就是降雨过程中或者降雨结束一定时间后浅层滑坡发生突然启动的内在原因。
在以上研究的基础上,提出边坡饱和临界时间tc的概念。认为,如果降雨持时小于 tc,则在整个降雨过程中坡体无法完全饱和;如果降雨持时大于tc,则在降雨过程结束前,坡体将达到完全饱和。对于后者而言,降雨过程结束时,边坡安全系数将一直处于最低点,这对边坡的稳定性极为不利,外部稍有扰动或岩土体自身强度降低到临界值即有发生滑坡的危险。这一临界时间在应用中可以结合实时降雨量的量测,对浅层滑坡的发生提供预警参数。
[1]刘新喜,夏元友,蔡俊杰,等.降雨入渗下强风化软岩高填方路堤边坡稳定性研究[J].岩土力学,2007,28(8):1705-1709.LIU Xin-xi,XIA Yuan-you,CAI Jun-jie,et al.Study of stability of high-filled embankment slope of highly weathered soft rock under rainfall infiltration[J].Rock and Soil Mechanics,2007,28(8):1705-1709.
[2]LUMB P.Slope failures in Hong Kong[J].Quarterly Journal of Engineering Geology and Hydrogeology,1975,8:31-65.
[3]李宁,许建聪,钦亚洲.降雨诱发浅层滑坡稳定性的计算模型研究[J].岩土力学,2012,33(5):1485-1490.LI Ning,XU Jian-cong,QIN Ya-zhou.Research on calculation model for stability evaluation of rainfallinduced shallow landslides[J].Rock and Soil Mechanics,2012,33(5):1485-1490.
[4]詹良通,李鹤,陈云敏,等.东南沿海残积土地区降雨诱发型滑坡预报雨强-历时曲线的影响因素分析[J].岩土力学,2012,33(3):872-880,886.ZHAN Liang-tong,LI He,CHEN Yun-min,et al.Parametric analyses of intensity-duration curve for predicting rainfall-induced landslides in residual soil slope in Southeastern coastal areas of China[J].Rock and Soil Mechanics,2012,33(3):872-880,886.
[5]胡明鉴,汪稔,张平仓.斜坡稳定性及降雨条件下激发滑坡的试验研究——以蒋家沟流域滑坡堆积角砾土坡地为例[J].岩土工程学报,2001,23(4):454-457.HU Ming-jian,WANG Ren,ZHANG Ping-cang.Primary research on the effect of rainfall on landslide—taking the slope piled by old landslide in Jiangjiagou valley as example[J].Chinese Journal of Geotechnical Engineering,2001,23(4):454-457.
[6]SKEMPTON A W,DELORY F A.Stability of natural slopes in London clay[C]//Proceedings of 4th International Conference on Soil Mechanics and Foundation Engneering.[S.l.][s.n.]1957:378-381.
[7]PRADEL D,RAAD G.Effect of permeability on surficial stability of homogeneous slopes[J].Journal of Geotechnical Engineering,1993,119(2):315-332.
[8]SUNG E C,SEUNG R L.Evaluation of surficial stability forhomogeneousslopesconsideringrainfall characteristics[J].Journal of Geotechnical and Geoenvironmental Engineering,2002,128:756-763.
[9]MEIN R G,LARSON C L.Modeling infiltration during a steady rain[J].Water Resources Research,1973,9(2):384-394.
[10]兰恒星,周成虎,李焯芬,等.瞬时孔隙水压力作用下的降雨滑坡稳定性响应分析:以香港天然降雨滑坡为例[J].中国科学E辑:技术科学,2003,33(增刊):119-136.
[11]许建聪,尚岳全,陈侃福,等.强降雨作用下的浅层滑坡稳定性分析[J].岩石力学与工程学报,2005,24(18):3246-3251.XU Jian-cong,SHANG Yue-quan,CHEN Kan-fu,et al.Analysis of shallow landslide stability under intensive rainfall[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(18):3246-3251.
[12]GREEN W H,AMPT C A.Studies on soil physics[J].Journal of Agriculture Science,1911,4(1):1-24.
[13]PHILIP J R.Hillslope infiltration:planar slopes[J].Water Resources Research,1991,27(1):109-117.
[14]LI C,MICHAEL H Y.Green-Ampt infiltration model for sloping surfaces[J].Water Resources Research,2006,42(7):1-9.
[15]顾成壮,胡卸文,张茂淳,等.强降雨下饱和平滑型滑坡坡体水流运动及其边坡稳定性效应分析——以四川汉源二蛮山滑坡为例[J].岩土力学,2013,34(4):1075-1081.GU Cheng-zhuang,HU Xie-wen,ZHANG Mao-chun,et al.Analysis of flow motion and its effect on the slope stability of plane sliding landslide saturated under heavy-rain—A case study of Ermanshan landslide in Hanyuan county of Sichuan province[J].Rock and Soil Mechanics,2013,34(4):1075-1081.
[16]何玉琼,徐则民,张勇,等.斜坡失稳的降雨阈值模型及其应用[J].岩石力学与工程学报,2012,31(7):1484-1490.HE Yu-qiong,XU Ze-min,ZHANG Yong,et al.Rainfall threshold model of rainfall-induced slope instability and its application[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(7):1484-1490.
[17]王靖泰,陈瑾,M塔捷亚娜,等.兰州附近黄土坡地的降雨模拟试验[J].中国地质灾害与防治学报,1993,4(3):44-52.WANG Jing-tai,CHEN Jin,MATIANA Muxart,et al.Rainfall simulation tests on loess slope of Golan Shan around Lanzhou[J].The Chinese Journal of Geological Harzard and Control,1993,4(3):44-52.
[18]雷志栋,杨诗秀,谢森传.土壤水动力学[M].北京:清华大学出版社,1988.
[19]杨文东.降雨型滑坡特征及其稳定分析研究[博士学位论文D].武汉:武汉理工大学,2006.
[20]李玉柱,苑明顺.流体力学[M].北京:高等教育出版社,1997.
[21]林鸿州.降雨诱发土质边坡失稳的试验与数值分析研究[博士学位论文D].北京:清华大学,2007.
[22]林鸿州,李广信,于玉贞,等.基质吸力对非饱和土抗剪强度的影响[J].岩土力学,2007,(9):1931-1936.LIN Hong-zhou,LI Guang-xin,YU Yu-zhen,et al.Influence of matric suction on shear strength behavior of unsaturated soils[J].Rock and Soil Mechanics,2007,28(9):1931-1936.
