振动频率和时间对扰动状态下软黏土压缩特性的影响

苗永红，范江桥，殷 杰

(江苏大学 土木工程与力学学院，江苏 镇江 212013)

软黏土广泛分布在我国沿海地区，由于经济快速发展，因此很多建筑物、隧道、高速公路、桥梁等不可避免地建设在软土地基之上。软黏土具有含水量大、孔隙比高、压缩性强、强度低、渗透性差等不利因素[1]，在外荷载作用下，土体破坏表现出较大的突发性，对工程安全造成潜在威胁。

建立在重塑土力学性质基础上的理论体系不能很好地用于实际工程，原因在于天然软黏土在沉积过程中产生了结构性，包括组构和颗粒间的黏结作用[2-3]，表现在原状土样相对重塑(完全扰动)土样在相同初始条件下具有更高的孔隙比和强度。在工程施工过程中，不可避免地对土体产生扰动作用，导致软土的结构性破坏，压缩性增强，强度降低，引发各类工程问题，因此需要探明扰动对软土结构性的影响规律和作用机制。国内外学者围绕扰动对软土的力学特性和结构性开展了大量的研究，取得了许多有意义的成果，如基于土的压缩特性提出扰动度的概念[4-6]，基于重塑土样提出土的固有压缩特性的概念[7]，基于强度提出灵敏度及触变性定量评价方法[8-9]等。已有的关于扰动影响的研究主要集中在扰动后软土的压缩强度等特性，少有研究关注施工机械的振动频率、振幅、时间等扰动源特性的影响。邓永锋等[10]的研究表明，振动时间对软土压缩特性有显著的影响。

本文中采用电磁振动台制备不同振动频率、时间条件下的扰动土样，对比原状土样及重塑土样，开展室内一维压缩试验，探讨振动频率、时间对不同扰动程度试样压缩性状的影响规律和作用机理。

1 试验

1.1 试验材料

试验土样取自江苏省连云港市某工程场地，采用内径、高度均为30 cm的大直径聚氯乙烯(PVC)管获取原状土样，取土深度为2.5 m，场地的地下水位为1.5 m。依据国家标准GB/T 50123—2019《土工试验方法标准》[11]测定土样的基本物理性质指标，结果如表1所示。由表可知，土样液限和塑限分别为56.4%和28.6%，相应的塑性指数为27.8。根据国家标准GB/T 50145—2007《土的工程分类标准》[12]，土样属于高液限黏土。

表1 试验土样的基本物理性质指标

1.2 试验方案

采用内径为6.18 cm、高度为2 cm的环刀，制备一组原状土样，并将环刀上、下用玻璃片封住，采用保鲜膜缠绕后，置于电磁振动台上，设置不同的振动频率和振动时间，制备不同扰动程度的土样，用于一维压缩试验，具体试验工况如下：振动时间分别为10、30、60 min，振动频率分别为1、5、10 Hz。为了对比，平行制备原状土样与重塑土样进行一维压缩试验。

2 结果与分析

图1所示为原状土样、重塑土样以及振动频率分别为1、5、10 Hz且振动时间分别为10、30、60 min时制得扰动土样的一维压缩曲线。从图中可以看出，原状土样的压缩曲线位于不同试验工况(振动频率、时间)时扰动土样压缩曲线的上方，随着竖向压力的增大，孔隙比随竖向压力的变化呈现出倒S型，与已有的天然原状土样的压缩曲线一致[4,13]。不同条件下的扰动土样也呈现出类似倒S型压缩曲线。一方面，当振动频率相同时，振动时间长的土样压缩曲线位于振动时间短的土样压缩曲线下方，并且振动时间越长，压缩曲线位置越低，表明当振动频率一定时，土样的压缩性随振动时间的增加而减弱，主要原因在于振动时间越长，振动传递到土样的能量越大，土样内部扰动越大，在相同竖向压力时的孔隙比越低；另一方面，当振动时间相同时，振动频率高的土样的压缩曲线位于振动频率低的压缩曲线下方，表明当振动时间一定时，土样的压缩性随振动频率的增加而减弱，主要原因在于振动频率越大，土样通过振动吸收的能量越大，土样内部扰动越大，导致在竖向压力相同时孔隙比有所降低。此外，重塑土样则呈现单线性压缩曲线，位于所有扰动土样压缩曲线的下方。原状土样以及不同程度的扰动土样的压缩曲线随着竖向压力的增大而逐渐与重塑土样的压缩曲线趋于一致。

e—孔隙比；p—竖向压力;1、5、10 Hz—振动频率；10、30、60 min—振动时间。图1 不同振动频率、时间时土样的e-lg p曲线

针对图1中的e-lgp(e为孔隙比，p为竖向压力)曲线，当采用传统的Cassagrande方法确定屈服压力时，最大曲率点难以确定，容易造成误差。采用ln(1+e)-lgp双对数坐标表示时，压缩曲线可以由双直线很好地表示[13]，双直线交叉点对应的竖向压力即为土的先期固结压力,如图2所示。从图中可以看出，原状土样的先期固结压力为64.7 kPa，而根据取样深度及土的天然重度，估算出土样的上覆压力约为29.5 kPa，超固结比为2.2，土样呈现出超固结土的性质。需要指出，连云港原状土样属于正常固结土，其先期固结压力大于土的上覆压力，原因是受到土结构性的影响。原状土样的超固结比被称为似超固结比或屈服应力比，与应力历史引起的超固结比本质上是不同的[14]。受到土结构性影响的天然软黏土的先期固结压力也被称为屈服压力py，当竖向压力小于py时，对应的压缩曲线段称为屈服前阶段，当竖向压力大于py时，对应的压缩曲线段称为屈服后阶段。图2中不同工况时扰动土样的压缩曲线在ln(1+e)-lgp坐标下均呈现出良好的双折线型，可以确定不同工况时扰动土样的屈服压力py。

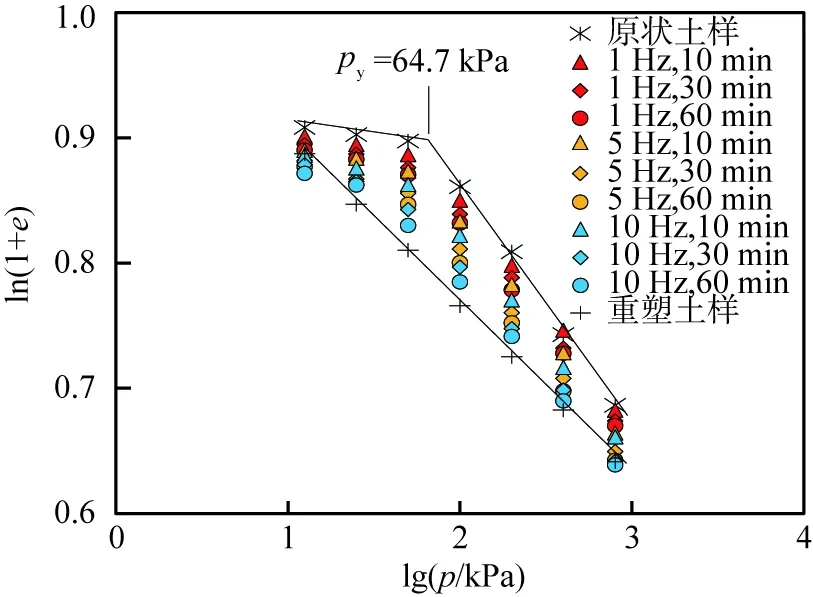
e—孔隙比；p—竖向压力；py—屈服压力；1、5、10 Hz—振动频率；10、30、60 min—振动时间。图2 不同振动频率、时间时土样的ln(1+e)-lg p曲线

图3所示为不同试验工况时屈服压力py随振动时间t和振动频率f的变化。从图中可以看出，一方面，当振动频率一定时，py随振动时间的增加而线性减小，并且振动频率越高，py越小；另一方面，当振动时间一定时，py随振动频率的增加而线性减小，并且振动时间越长，py越小。当振动时间从10 min增至30 min且振动频率为1 Hz时，py从63.2 kPa减小到62 kPa，减小了1.7%，而当振动频率为10 Hz时，py从58.1 kPa减小到49.1 kPa，减小了15.4%。当振动时间从10 min增至30 min且振动频率从1 Hz增至10 Hz时，py减小的幅度从1.7%变为15.4%，表明屈服压力受振动频率和时间的影响较显著，主要原因是原状土样在高频率、长时间的振动作用下，振动对土样施加的扰动能量增加，土样内部结构的扰动程度逐渐增加，结构性的影响因扰动而逐渐减少。

为了定量评价土体的扰动程度，Hong等[4]基于土样在ln(1+e)-lgp坐标下的压缩曲线，提出扰动度D的定量计算公式[4]，即

(1)

式中：Cclb为扰动土样屈服前压缩指数，即扰动土样在屈服前阶段压缩曲线的斜率；Cclr为重塑土样压缩指数，即重塑土样在ln(1+e)-lgp坐标下的压缩曲线的斜率。扰动度D定义示意图如图4所示。通过开展一维压缩试验可以确定扰动土样在不同工况时的Cclb和Cclr，代入式(1)即可计算得到扰动度D。

e—孔隙比；Cclb、Ccla—扰动土样屈服前、后压缩指数；Cclr—重塑土样压缩指数；py—屈服压力。图4 扰动度D定义示意图

图5所示为屈服压力py随扰动度D的变化。从图中可看出，扰动引起py呈线性减小，关系式为

py=-0.58D+73.1。

(2)

图6所示为扰动度随振动时间和振动频率的变化。从图中可以看出，D随振动时间和振动频率的增加而呈现线性增加的趋势。本文中扰动度与振动时间的关系数据与文献[10]中连云港软土扰动度与振动时间的关系数据进行对比，即振动时间为30、60、90 min时的扰动度分别为11.9%、20.5%、29.4%，得出D随振动时间和振动频率的增加而呈现线性增大的结论。主要原因是土样在振动时间和振动频率增加的情况下，土样结构发生扰动，并且扰动程度越来越大。

R—相关系数。图5 屈服压力py随扰动度D的变化

图7、8所示分别为Cclb、扰动土样屈服后压缩指数Ccla随振动时间和振动频率的变化。从图7(a)中可以看出，当振动频率一定时，随着振动时间的增加，Cclb不断增大。本文中扰动土样屈服前压缩指数Cclb、振动时间的数据与文献[10]中连云港软土扰动土样屈服前压缩指数Cclb、振动时间数据进行对比，即振动时间为30、60、90 min时，扰动土样屈服前压缩指数Cclb分别为0.027、0.046、0.065，得出扰动土样屈服前压缩指数Cclb随振动时间的增加而呈现线性增加的结论。从图7(b)中可以看出，随着振动频率的增加，Cclb不断增大。从图8(a)中可以看出，随着振动时间的增加，Ccla不断减小，频率增加导致振动频次增加，因此土样吸收能量增加。从图8(b)中可以看出，随着振动频率的增加，Ccla不断减小。

Burland[7]采用孔隙指数将初始含水质量分数为液限的1.0～1.5倍的重塑土样压缩曲线归一化为固有压缩曲线(ICL)，孔隙指数Iv[7]为

(3)

(4)

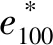
经过大量数据拟合，得到ICL定量表达式[7]为

Iv=2.45-1.285lgp+0.015(lgp)3。

(5)

采用孔隙指数Iv将不同试验工况(振动频率、时间)时获得的压缩曲线进行处理，结果如图9所示。从图中可以看出，重塑土样的压缩曲线很好地归一化为ICL，原状土样Iv-lgp曲线位于所有曲线最上方，屈服前变化较小，屈服后随着p的增加，各工况时的Iv-lgp曲线逐渐与ICL重合，其他工况时的Iv-lgp曲线介于重塑土样和原状土样的Iv-lgp曲线之间，扰动土样屈服前的Iv-lgp曲线位置缓慢降低，扰动土样屈服后的Iv-lgp曲线位置降低幅度逐渐增加，部分曲线在p较小时穿过ICL。

Iv—孔隙指数；ICL—固有压缩曲线；p—竖向压力；1、5、10 Hz—振动频率；10、30、60 min—振动时间。图9 不同振动频率、时间时土样的Iv-lg p曲线

一方面，在振动频率相同时，振动时间长的土样的Iv-lgp曲线位于振动时间短的土样的Iv-lgp曲线下方，并且振动时间越长，压缩曲线位置越低；另一方面，在振动时间相同时，振动频率高的土样的Iv-lgp曲线位于频率低的压缩曲线的下方，说明随着振动时间和振动频率的增加，土样结构破坏越严重，越接近重塑土状态。

3 结论

通过开展不同扰动程度的软黏土试样的一维压缩试验，研究了振动频率、振动时间对不同扰动程度土样的压缩特性的影响规律及作用机制，主要结论如下：

1)在相同的振动频率条件下，由压缩曲线获得的扰动土样屈服后压缩指数Ccla、屈服压力py随着振动时间增加而逐渐减小，屈服前压缩指数Cclb和扰动度D随时间增加而逐渐增大，并且屈服压力py随着扰动度的增加呈线性衰减关系。

2)在相同的振动时间条件下，振动频率高的土样压缩曲线位于振动频率低的下方，随着振动频率的提高，软黏土相应的压缩性、扰动土样屈服后压缩指数Ccla、屈服压力py逐渐减小，而扰动土样屈服前压缩指数Cclb和扰动度D则随振动频率增大而逐渐增大。

3)Burland[7]提出的孔隙指数可以将重塑土样压缩曲线归一化为ICL，不同扰动程度的土样压缩曲线位于ICL上方，扰动土样屈服前Iv-lgp曲线位置缓慢降低，扰动土样屈服后Iv-lgp曲线位置降低幅度增大，随着振动频率和振动时间的增加，不同扰动程度的Iv-lgp曲线都逐渐接近于ICL曲线。