基于Bootstrap方法的岩土体参数联合分布模型识别

唐小松 ，李典庆 ，周创兵 ，方国光

（1.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2.武汉大学 水工岩石力学教育部重点实验室，湖北 武汉 430072）

1 引 言

岩土工程可靠度分析中经常包含相关非正态变量，如岩土体的抗剪强度参数黏聚力和内摩擦角间存在统计负相关性[1－2]、基桩荷载-位移双曲线参数具有负相关性[3－5]，非饱和土的土-水特征曲线参数亦具有明显的负相关关系[6]，而且这些参数一般都服从非正态分布。众所周知，岩土工程可靠度分析通常需要已知相关非正态岩土体参数的联合概率分布函数。近年来，Copula理论[7]为相关非正态岩土体参数联合概率分布函数的建立提供了一种新的途径，它在岩土工程领域中逐渐得到应用[8－10]。究其原因，在Copula理论框架下构造岩土体参数联合概率分布函数具有以下2方面不可替代的优点[7]：其一是该方法将岩土体参数联合概率分布函数的构造简化为岩土体参数边缘分布函数估计和Copula函数选择问题，且边缘分布函数估计和Copula函数选择分开独立进行；其二是该方法能够将不同类型的边缘分布函数和Copula函数结合在一起，从而构造出具有任意边缘分布函数及任意相关结构岩土体参数的联合概率分布函数。鉴于Copula理论的上述优点，本文主要研究基于Copula理论的相关非正态岩土体参数联合概率分布函数构造方法。

基于Copula理论的岩土体参数联合概率分布函数构造方法中，岩土体参数的最优边缘分布函数和最优Copula函数都是基于实测数据采用AIC（Akaike information criterion）准则[11]优化比较选择确定的，即具有最小AIC 值的边缘分布函数和Copula函数被认为是拟合原始观测数据概率分布特性和相关结构最优的概率分布模型。AIC 准则中的AIC 值是岩土体参数实测数据的函数，因此，是样本的函数。而样本是一个N 维随机向量，N为样本容量，从而样本的函数亦是一个随机变量，这个随机变量称为统计量。统计量的变异性大小由样本容量决定，样本容量越小，变异性越大。一般来说，样本数目小于100时属于小样本容量。岩土体参数具有小样本容量是岩土工程中一个客观存在的事实[1－6]，基于有限岩土体参数试验数据计算得到的AIC 值通常具有较大的变异性。传统方法没有考虑AIC 值的变异性，而仅仅基于岩土体参数实测数据求得不同备选边缘分布函数和Copula函数的单一AIC值识别最优边缘分布函数和最优Copula函数。众所周知，随机变量的单一取值并不能代表这个变量的实际分布，因而基于单一AIC 值的最优边缘分布函数和最优Copula函数识别方法是不合理的。为了得到合理的识别结果，应该充分考虑小样本容量岩土体参数引起的统计量AIC 值的变异性，其关键难点主要体现在以下两方面：①已知岩土体参数实测数据如何模拟AIC 值的变异性；②考虑AIC 值变异性时如何表述识别结果。对于上述问题，迄今为止还未见系统的研究。

近年来在统计学领域应用较多的Bootstrap方法[12]为小样本条件下统计量分布的直接模拟提供了一种新的工具。Bootstrap方法最早由Efron[12]于1979年提出，近年来在岩土工程领域中得到了应用[13－14]；如谢桂华等[13]采用Bootstrap方法模拟了地基沉降计算经验系数均值的分布及置信区间；Luo等[14]利用Bootstrap方法研究了小样本容量引起的土性参数统计量变异性对支护开挖失效概率的影响。Bootstrap方法的基本思想是通过对原始观测样本数据进行有放回地随机抽样得到大量与原始观测样本相同样本容量的Bootstrap子样本，然后基于Bootstrap子样本计算统计量的估计值，最终获得统计量的变异系数及其概率分布。该方法只依赖于给定的原始观测样本数据，且能够充分挖掘原始观测数据所携带的总体信息，不需要对岩土体参数的实际分布作任何假设以及增加新的数据观测，因此，该方法是一种非参数统计方法。从本质上说，Bootstrap方法是一种将小样本问题转化为大样本问题的分析方法。鉴于Bootstrap方法的上述优势，本文将Bootstrap方法应用于小样本容量岩土体参数AIC 值分布的模拟问题，提出了基于Bootstrap方法的岩土体参数最优边缘分布函数和最优Copula函数识别方法。最后以基桩荷载-位移双曲线参数试验数据为例证明了所提方法的有效性。

2 岩土体参数联合分布函数构造的Copula函数方法

本文采用Copula函数构造岩土体参数的联合概率分布函数，下面简要介绍Copula函数基本定义以及基于Copula函数的岩土体参数联合概率分布函数构造方法。Copula函数是将变量的联合分布与其边缘分布联结起来的函数，它惟一地描述了变量间相关性信息，包括变量间相关系数大小以及变量间相关结构类型。对于二维情况，Copula函数定义为[0，1]2空间中边缘分布为[0，1]区间内均匀分布的二维联合概率分布函数[7]：

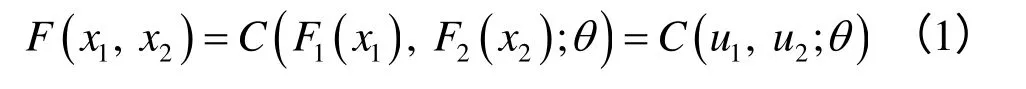
式中：F(x1，x2)为变量X1和X2的联合概率分布函数；u1=F1(x1)和u2=F2(x2)分别为变量X1和X2的边缘分布函数；C为Copula函数；θ为Copula函数的相关参数。相应地，若已知变量X1和X2的概率密度函数f1(x1)和f2(x2)，则通过对式（1）两边求导可得变量X1和X2的联合概率密度函数f (x1，x2)为

式中：c（F1（x1），F2（x2）;θ）=∂2C（u1，u2;θ）/∂u1∂u2，为Copula密度函数。因此，若已知变量X1和X2的边缘分布函数和Copula函数，利用式（1）和式（2）就可以建立变量X1和X2的二维联合概率分布模型。Copula函数的相关参数θ 可由变量X1和X2间的Kendall秩相关系数τ 由下式直接求出[7]：

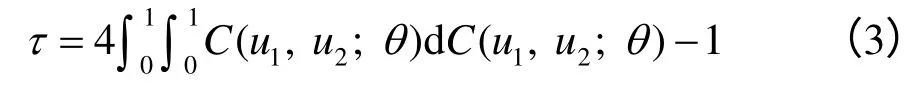
因此，当变量X1和X2间的Kendall秩相关系数τ 已知时，通过求解式（3）所示的非线性积分方程就可得出参数θ 。从式（1）和式（2）可以看出，相关非正态岩土体参数联合概率分布模型的建立包括2个步骤：第1步是建立岩土体参数的边缘分布函数；第2步是选择最优的Copula函数描述岩土体参数间的相关结构。如前所述，上述2步可以分开独立进行，下面分别给出岩土体参数最优边缘分布函数和最优Copula函数识别方法。

本文采用工程上常用的AIC准则[11]识别最优的边缘分布函数，即具有最小AIC 值的边缘分布函数被认为是拟合原始观测数据概率分布特性最优的边缘分布函数。AIC 值定义为变量原始观测数据点处概率密度函数值对数和的-2倍与2倍概率密度函数分布参数数目之和，表达式为

式中：ε为边缘分布函数的分布参数向量；k1为边缘分布函数中分布参数的数目；N为原始观测数据的样本容量。因此，已知岩土体参数的一组观测数据，就可以采用式（4）求出多种备选边缘分布函数的AIC 值，从而识别出拟合原始观测数据概率分布特性最优的边缘分布函数。本文选取岩土工程中常用的正态分布、对数正态分布、极值I型分布和威布尔分布作为备选边缘分布函数拟合岩土体参数的概率分布特性[15－18]。为了避免出现负值，正态分布和极值I型分布在0处进行左截尾。上述4种边缘分布函数都包含2个分布参数，因此k1=2，这些分布参数ε 可以利用岩土体参数观测数据的均值和标准差求出。

最优的Copula函数也可以采用AIC准则[11]识别，即具有最小AIC 值的Copula函数被认为是拟合原始观测数据相关结构最优的Copula函数。AIC 值定义为变量原始观测数据点处Copula密度函数值对数和的-2倍与2倍Copula函数相关参数数目之和，表达式为

式中：k2为Copula函数中相关参数的数目，对于二维Copula函数来说k2=1；(u1i，u2i)，为原始观测数据(x1i，x2i)的经验分布值，可由下式计算：

式中：rank(x1i)和rank(x2i)分别为按升序排列时实测值x1i和x2i在整列观测数据x1={x11，x12，···，x1N}和x2={x21，x22，···，x2N}中的秩次。因此，已知岩土体参数的一组观测数据，就可以采用式（5）求出多种备选Copula函数的AIC 值，从而识别出拟合原始观测数据相关结构最优的Copula函数。本文选取岩土工程中常用的Gaussian、Plackett、Frank和No.16 Copula函数作为备选Copula函数拟合岩土体参数间的相关结构[8－10]。上述4种Copula函数都能描述变量间的负相关性，且相关系数都能达到-1，它们非常适合描述负相关性较强的岩土体参数间相关关系[8－10]。这些Copula函数的相关参数θ 可以利用岩土体参数观测数据的Kendall秩相关系数由式（3）求出。

从式（4）和式（5）可以看出各备选边缘分布函数和Copula函数的AIC值都是岩土体参数试验数据的函数，因此，都是样本的函数。由统计学理论可知，样本是一个N 维随机向量，从而AIC 值这个样本的函数亦是一个随机变量，它称为统计量。统计量的变异性大小由样本容量决定，样本容量越小变异性越大。实际工程中岩土体参数试验数据通常具有较小的样本容量，基于这些有限试验数据计算得到的AIC 值具有较大的变异性。传统方法没有考虑AIC 值变异性，而仅仅基于岩土体参数实测数据求得不同备选边缘分布函数和Copula函数的单一AIC 值识别最优边缘分布函数和Copula函数。众所周知，随机变量的单一取值并不能代表这个变量的实际分布，因而基于单一AIC 值的最优边缘分布函数和Copula函数识别方法是不合理的。为了得到合理结果，应该充分考虑小样本容量岩土体参数引起的统计量AIC 值的变异性。下面介绍统计量AIC 值变异性模拟的Bootstrap方法以及基于Bootstrap的最优边缘分布函数和Copula函数识别方法。

3 岩土体参数联合分布函数识别的Bootstrap方法

本文采用Bootstrap方法模拟统计量AIC值的变异性，下面简要介绍Bootstrap方法基本原理以及基于Bootstrap的岩土体参数最优边缘分布函数和最优Copula函数识别方法。Bootstrap方法最早由Efron[12]于1979年提出。它通过对原始观测样本数据进行有放回地随机抽样获得大量Bootstrap子样本，然后基于这些子样本计算统计量的估计值，最终获得统计量的变异系数及其概率分布。该方法只依赖于给定的岩土体参数的原始观测样本，且能够充分挖掘原始观测样本所携带的岩土体参数总体信息，不需要对岩土体参数的实际分布作任何假设和增加新的数据观测。尽管简单，但该方法的理论依据及其良好的收敛性早已被统计学家所证明[12]。Bootstrap方法不仅被证明对于大部分统计量满足大样本的相合性，而且对于小样本分析更具有不可替代的优越性。基于Bootstrap的统计量AIC 值的变异性模拟主要包括以下3步：

（1）令岩土体参数的原始观测样本数据为X0={(x1i，x2i)，i=1，2，···，N}，从中有放回地随机抽样N次，每次抽取岩土体参数的一次观测，从而得到第1个与X0相同样本容量的Bootstrap子样本

（2）重复上述步骤B 次，即可获得B 个Bootstrap子样本i=1，2，···，N;b=1，2，···，B}；

（3）基于每个Bootstrap子样本估计岩土体参数的样本均值、标准差和Kendall秩相关系数，然后采用式（4）和式（5）分别计算4种备选边缘分布函数和Copula函数的AIC 值，从而得到AIC 值的变异系数及其概率分布。

一般来说，为了达到良好的收敛效果，Bootstrap子样本数目通常取值较大。如文献[14]研究表明，B=104时能够保证Bootstrap模拟的土性参数的样本均值和标准差收敛于总体均值和标准差。因此，本文亦采用B=104模拟AIC 值的变异性。基于每个Bootstrap子样本计算的4种备选边缘分布函数和Copula函数的AIC 值即可识别出该子样本的最优边缘分布函数和最优Copula函数。统计所有B个Bootstrap子样本的4种备选边缘分布函数和Copula函数被识别为最优边缘分布和最优Copula的次数[19－20]，从而得到4种备选边缘分布函数和Copula函数为最优边缘分布和最优Copula的权重系数。与传统方法不同，本文在考虑AIC 值变异性基础上，将识别结果表示为4种备选边缘分布函数，Copula函数被识别为最优边缘分布和最优Copula的权重系数集合。这种表述方法充分考虑了小样本容量岩土体参数引起的AIC 值的变异性，从而更加合理地描述了岩土体参数最优边缘分布函数和最优Copula函数识别结果。与传统方法一样，本文方法得出的识别结果亦可直接代入岩土工程可靠度分析中，从而反映小样本容量岩土体参数引起的AIC 值变异性对岩土结构物可靠度结果的影响。

4 算 例

4.1 基桩荷载-位移双曲线参数试验数据

本文以基桩荷载-位移双曲线参数试验数据为例，研究Bootstrap方法在小样本岩土体参数最优边缘分布函数和最优Copula函数识别中的应用。对于基桩荷载-位移关系的预测问题，国内外研究人员提出了多种基桩荷载-位移关系曲线模型，如双曲线模型、幂函数模型、指数函数模型、GM（1，1）模型等，其中双曲线模型在基桩中应用最为广泛。原因在于双曲线模型中参数较少，而且物理意义明确。为了降低实测基桩荷载-位移双曲线数据的离散性，文献[3－5]提出了采用标准化的荷载-位移双曲线模型去表征实测荷载-位移关系曲线，该标准化的荷载-位移双曲线模型为

式中：Q为轴向荷载；QSTC为基桩实测极限承载力；y为桩端位移；a 和b 是双曲线两个参数，它们具有明确的物理意义，其中a为双曲线初始斜率的倒数，b为双曲线极限值的倒数，其物理意义见图1。

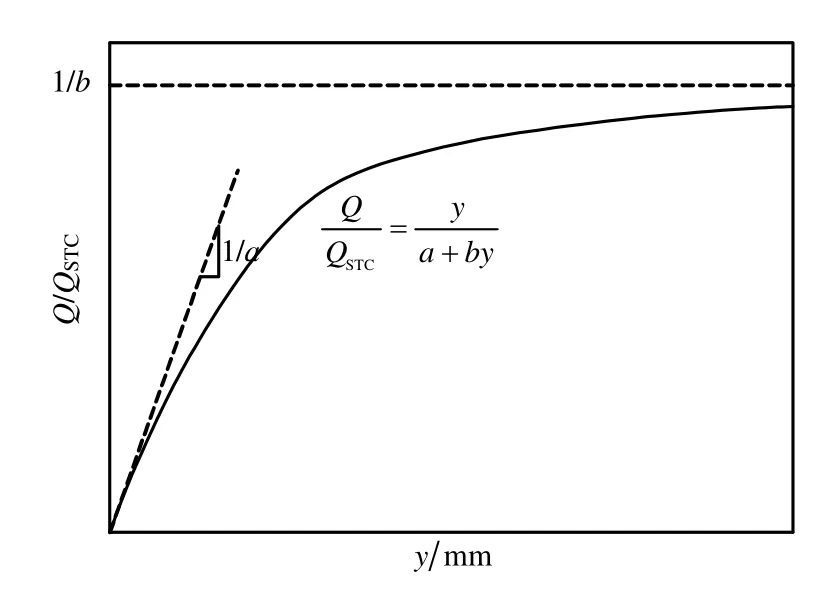
图1 基桩标准化荷载-位移双曲线模型Fig.1 Definition of the normalized hyperbolic load-settlement curve of foundation pile

考虑文献[5]中4类基桩荷载-位移双曲线参数试验数据，这4类数据分别是无黏性土中打入桩（D-NC）、无黏性土中灌注桩（B-NC）、黏性土中打入桩（D-C）和黏性土中灌注桩（B-C），它们的样本容量分别为28、30、59和53，可见这些数据都属于小样本容量数据。图2给出了上述4类双曲线参数数据a 和b 的散点图。由这些数据计算的双曲线参数的均值、标准差和相关系数见表1。可以看出，双曲线参数具有明显的负相关关系，它们的Kendall秩相关系数分别为-0.597、-0.750、-0.740和-0.755。基于这些数据采用本文方法就可以模拟AIC 值的变异性并识别出拟合数据概率分布特性和相关结构最优的边缘分布函数和Copula函数，从而建立双曲线参数a 和b 的联合概率分布模型，为基桩正常使用极限状态可靠度分析奠定基础[8]。

图2 双曲线参数试验数据的散点图Fig.2 Scattering plots of the measured parameters of the hyperbolic curve

表1 双曲线参数试验数据的统计特性Table 1 Statistical properties of the measured parameters of the hyperbolic curve

4.2 双曲线参数最优边缘分布函数的识别

在采用本文方法识别双曲线参数a 和b 的最优边缘分布函数之前，首先给出基于传统方法的最优边缘分布函数识别结果。为此，表2给出了基于双曲线参数原始观测样本数据（见图2）计算的4种备选边缘分布函数的单一AIC 值。可以看出，除了B-C数据的参数a 和D-NC数据的参数b 最优边缘分布函数分别是极值I型分布和对数正态分布外，其余数据参数a 和b 的最优边缘分布都是威布尔分布。可见，采用威布尔分布能够较好地描述双曲线参数试验数据的概率分布特性。

下面采用本文方法识别双曲线参数a 和b 的最优边缘分布函数。在给出AIC 值的概率分布之前，首先研究小样本数据对样本均值和标准差的影响。图3给出了基于Bootstrap模拟的参数a 的样本均值和标准差概率密度函数。为了比较，图中还给出了基于参数a 的原始观测数据计算的样本均值和标准差（见竖直线）。可以看出，小样本岩土体参数数据的样本均值和标准差具有较大的离散性，如D-NC、B-NC、D-C和B-C数据的样本均值变异系数分别为0.10、0.14、0.07和0.10，它们的样本标准差变异系数分别为0.14、0.11、0.10和0.22。总的来说，小样本岩土体参数数据对样本标准差变异性的影响要大于对样本均值的影响，这符合统计学理论的一般规律。此外，基于参数a 的原始观测数据计算的样本均值和标准差仅仅是样本均值和标准差实际分布的单一取值，该取值能够较好地被Bootstrap方法所模拟。因此，Bootstrap方法除了保留原始观测数据的相关特性外，还能充分挖掘原始观测数据所隐藏的总体信息，这也是Bootstrap方法被广泛应用于统计量变异性模拟的原因所在。同理，采用本文方法可以得出参数b 的样本均值和标准差的概率密度函数，限于篇幅，这里不再列出。小样本岩土体参数数据样本均值和标准差的这种变异性将直接导致计算的边缘分布函数AIC 值具有较大变异性，这是因为计算AIC 值时各备选边缘分布函数的分布参数都是基于样本均值和标准差确定的。

图3 参数a 的样本均值和标准差概率密度函数Fig.3 PDFs of mean and standard deviation of a

为了研究小样本岩土体参数试验数据对AIC 值变异性的影响，图4以参数a为例给出了4种备选边缘分布函数AIC 值的概率密度函数。小样本岩土体参数试验数据对AIC 值变异性具有重要的影响，如B-C数据计算的正态分布、对数正态分布、极值I型分布和威布尔分布AIC 值的变异系数分别为0.10、0.14、0.08和0.08。不同边缘分布函数AIC值的概率密度函数重叠区域较大，这进一步说明识别最优边缘分布函数时4种备选边缘分布都有可能被识别为最优的边缘分布函数。传统方法基于单一AIC 值识别最优的边缘分布函数忽略了其余备选边缘分布函数为最优边缘分布的概率，因此，是不合理的。此外，基于参数a 的原始观测数据计算的边缘分布函数AIC 值是实际分布的单一取值，该取值亦能较好地被Bootstrap方法所模拟。

为了充分考虑不同备选边缘分布为最优边缘分布的概率，表3给出了104个Bootstrap子样本中4种备选边缘分布被识别为最优边缘分布的次数及权重系数。可以看出，由于小样本岩土体参数试验数据的影响，没有一种备选边缘分布能够被100%地识别为最优的边缘分布函数。除了B-C数据的参数a 和D-NC数据的参数b 权重系数最大边缘分布分别是极值I型分布和对数正态分布外，其余数据参数a 和b 的权重系数最大边缘分布都是威布尔分布。上述结果与传统方法识别结果保持了较好的一致性。然而，传统方法没有考虑其余备选边缘分布函数为最优边缘分布的概率。如对于D-NC数据的参数b 来说，除去对数正态分布后其余3种备选边缘分布函数为最优边缘分布的概率达到了64.40%。因此，本文提出的基于Bootstrap的岩土体参数最优边缘分布函数识别方法比传统方法要优越。

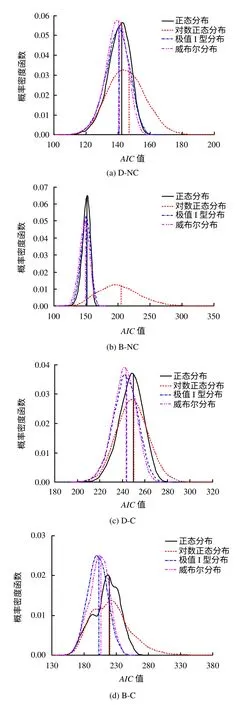
图4 不同边缘分布计算的参数a 的AIC 值概率密度函数Fig.4 PDFs of AIC values of various margins for a

表2 基于双曲线参数试验数据计算的4种备选边缘分布函数AIC 值Table 2 AIC values associated with various margin distribution functions using the measured data for hyperbolic curve-fitting parameters

表3 10 000个Bootstrap子样本中不同边缘分布被识别为最优边缘分布的次数及权重系数Table 3 Numbers of times and weight factors being the best-fit one for different margin distribution functions over 10 000 bootstrap samples

4.3 双曲线参数最优Copula函数的识别

在采用本文方法识别双曲线参数a 和b 间最优Copula函数前，首先给出基于传统方法的最优Copula函数识别结果。为此，表4给出了基于双曲线参数原始观测数据计算的4种备选Copula函数的单一AIC 值。可以看出，对于D-NC数据来说，Gaussian Copula函数计算的AIC 值最小，它是拟合D-NC数据间相关结构最优的Copula函数。而对于B-NC、D-C和B-C数据来说，最优的Copula函数都是Plackett Copula函数。因此，大部分情况下采用Plackett Copula函数能够较好地描述双曲线参数试验数据的相关结构。

表4 基于双曲线参数试验数据计算的4种备选Copula函数AIC 值Table 4 AIC values associated with various Copula functions using measured data for hyperbolic curve-fitting parameters

下面采用本文方法识别双曲线参数a 和b 间最优Copula函数。在给出AIC 值的概率分布之前，首先研究小样本岩土体参数试验数据对相关系数的影响。图5给出了基于Bootstrap模拟的参数a 和b间Kendall秩相关系数的概率密度函数。图中同时给出了基于参数a 和b 的原始观测样本数据计算的Kendall秩相关系数。可以看出，小样本岩土体参数试验数据的相关系数亦具有较大的离散性，如D-NC、B-NC、D-C和B-C数据的相关系数变异系数分别为0.19、0.12、0.06和0.08。此外，基于参数a 和b 的原始观测样本数据计算的Kendall秩相关系数仅仅是相关系数实际分布的单一取值，该取值亦能够较好地被Bootstrap方法所模拟。Bootstrap方法不仅能够重复原始观测样本数据的Kendall秩相关系数，它还能模拟相关系数的变异性及其概率分布。小样本岩土体参数试验数据相关系数的这种变异性将直接导致计算的Copula函数AIC值具有较大变异性，这是因为计算AIC 值时各备选Copula函数的相关参数都是基于Kendall秩相关系数采用式（3）确定的。

图5 双曲线参数间相关系数的概率密度函数Fig.5 PDFs of correlation coefficient between a and b

图6给出了4种备选Copula函数计算的AIC值概率密度函数。可以看出，小样本岩土体参数试验数据对AIC 值变异性具有重要的影响，如样本容量最小的D-NC数据计算的Gaussian、Plackett、Frank和No.16 Copula函数AIC 值的变异系数分别为0.40、0.41、0.42和0.65。可见二维Copula函数AIC 值变异系数明显大于一维边缘分布函数AIC 值变异系数。与边缘分布函数一样，不同Copula函数AIC 值的概率密度函数重叠区域较大，识别最优Copula函数时4种备选Copula函数都有可能被识别为最优的Copula函数。传统方法忽略了其余备选Copula函数为最优Copula的概率，因此，是不合理的。同理，基于参数a 和b 的原始观测数据计算的不同备选Copula函数AIC值是实际分布的单一取值，该取值能较好地被Bootstrap所模拟。此外，Bootstrap方法还能有效模拟AIC 值变异性及其概率分布，这是传统方法所无法比拟的。

为了考虑不同备选Copula函数为最优Copula的概率，表5给出了104个Bootstrap子样本中4种备选Copula函数被识别为最优Copula的次数及权重系数。由于小样本岩土体参数试验数据的影响，4种备选Copula函数都不能被100%地识别为最优的Copula函数。对于D-NC数据而言，权重系数最大的Copula函数是Gaussian Copula。对于D-C数据来说，权重系数最大的Copula函数是Frank Copula。而B-NC和B-C数据权重系数最大的Copula函数都是Plackett Copula。除了样本容量最大的D-C数据外，上述结果与传统方法识别结果亦保持了较好的一致性。由于传统方法没有考虑AIC 值变异性，由传统方法识别的D-C数据最优的Plackett Copula函数的权重系数只有17.87%，远低于非最优的Frank Copula函数的66.14%。可见，传统方法容易给出错误的识别结果。此外，传统方法亦没有考虑其余备选Copula函数为最优Copula的概率。如对于B-NC数据来说，除去Plackett Copula函数后其余3种备选Copula函数为最优Copula的概率达到了54.01%。因此，本文提出的基于Bootstrap的岩土体参数最优Copula函数识别方法远比传统方法优越。

图6 不同Copula函数计算的AIC 值概率密度函数Fig.6 PDFs of AIC values of various Copulas functions

表5 10 000个Bootstrap子样本中不同Copula函数被识别为最优Copula的次数及权重系数Table 5 Numbers of times and weight factors being best-fit Copula function for different Copula functions over 10 000 bootstrap samples

5 结 论

（1）Bootstrap方法能够有效地模拟统计量的变异性及其概率分布，该方法只依赖于岩土体参数的原始观测样本数据，且能够充分挖掘原始观测样本所携带的岩土体参数总体信息，不需要对岩土体参数的实际分布作任何假设以及增加新的数据观测，它为小样本容量岩土体参数统计量的变异性模拟提供了一条有效的途径。

（2）提出的基于Bootstrap的最优边缘分布函数和最优Copula函数识别方法，不仅可以有效地考虑统计量AIC 值的变异性，而且能够综合地反映不同备选边缘分布函数和Copula函数为最优边缘分布和最优Copula的概率，相比传统的基于单一AIC值的最优边缘分布函数和最优Copula函数识别方法要优越，建议优先采用。

（3）基于小样本容量岩土体参数试验数据估计的样本均值、标准差和相关系数具有较大的离散性，这种离散性进一步导致了识别最优边缘分布函数和最优Copula函数时统计量AIC 值存在较大的变异性。为了提高岩土体参数最优边缘分布函数和最优Copula函数的识别精度，建议尽可能多地收集岩土体参数试验数据。

（4）尽管Bootstrap方法只依赖于给定的岩土体参数原始观测样本数据，该原始观测样本的样本容量以及数据质量仍对最优边缘分布函数和最优Copula函数的识别结果有重要的影响。为了使得识别结果收敛于总体情况，建议采取合理措施保证原始观测样本数据的代表性和准确性。

[1]范明桥，盛金保.土强度指标φ，c 的互相关性[J].岩土工程学报，1997，19(4):100－104.FAN Ming-qiao，SHENG Jin-bao.Cross correlation of soil strength indexes φ and c[J].Chinese Journal of Geotechnical Engineering，1997，19(4):100－104.

[2]TANG X S，LI D Q，CHEN Y F，et al.Improved knowledge-based clustered partitioning approach and its application to slope reliability analysis[J].Computers and Geotechnics，2012，45:34－43.

[3]PHOON K K，KULHAWY F H.Characterization of model uncertainties for laterally loaded rigid drilled shafts[J].Geotechnique，2005，55(1):45－54.

[4]DITHINDE M，PHOON K K，DE WET M，et al.Characterization of model uncertainty in the static pile design formula[J].Journal of Geotechnical and Geoenvironmental Engineering，2011，137(1):70－85.

[5]LI D Q，TANG X S，PHOON K K，et al.Bivariate simulation using Copula and its application to probabilistic pile settlement analysis[J].International Journal for Numerical and Analytical Methods in Geomechanics，2013，37(6):597－617.

[6]PHOON K K，SANTOSO A，QUEK S T.Probabilistic analysis of soil-water characteristic curves[J].Journal of Geotechnical and Geoenvironmental Engineering，2010，136(3):445－455.

[7]NELSEN R B.An introduction to Copulas[M].New York:Springer，2006.

[8]唐小松，李典庆，周创兵，等.基于Copula函数的基桩荷载-位移双曲线概率分析[J].岩土力学，2012，33(1):171－178.TANG Xiao-song，LI Dian-qing，ZHOU Chuang-bing，et al.Probabilistic analysis of load-displacement hyperbolic curves of single pile using Copula[J].Rock and Soil Mechanics，2012，33(1):171－178.

[9]唐小松，李典庆，周创兵，等.基于Copula函数的抗剪强度参数间相关性模拟及边坡可靠度分析[J].岩土工程学报，2012，34(12):2284－2291.TANG Xiao-song，LI Dian-qing，ZHOU Chuang-bing，et al.Modeling dependence between shear strength parameters using Copulas and its effect on slope reliability[J].Chinese Journal of Geotechnical Engineering，2012，34(12):2284－2291.

[10]唐小松，李典庆，周创兵，等.不完备概率信息条件下边坡可靠度分析方法[J].岩土工程学报，2013，35(6):1027－1034.TANG Xiao-song，LI Dian-qing，ZHOU Chuang-bing，et al.Reliability analysis of slopes with incomplete probability information[J].Chinese Journal of Geotechnical Engineering，2013，35(6):1027－1034.

[11]AKAIKE H.A new look at the statistical model identification[J].IEEE Transactions on Automatic Control，1974，19(6):716－723.

[12]EFRON B.Bootstrap methods:another look at the jackknife[J].The Annals of Statistics，1979，7(1):1－26.

[13]谢桂华，张家生，刘荣桂.沉降计算经验系数的Bootstrap法置信区间估计[J].中南大学学报(自然科学版)，2011，42(9):2843－2847.XIE Gui-hua，ZHANG Jia-sheng，LIU Rong-gui.Estimation of confidence interval of empirical coefficients in calculating foundation settlement by Bootstrap method[J].Journal of Central South University(Science and Technology)，2011，42(9):2843－2847.

[14]LUO Z，ATAMTURKTUR S，JUANG C H.Bootstrapping for characterizing the effect of uncertainty in sample statistics for braced excavations[J].Journal of Geotechnical and Geoenvironmental Engineering，2013，139(1):13－23.

[15]陈立宏，陈祖煜，刘金梅.土体抗剪强度指标的概率分布类型研究[J].岩土力学，2005，26(1):37－40.CHEN Li-hong，CHEN Zu-yu，LIU Jin-mei.Probability distribution of soil strength[J].Rock and Soil Mechanics，2005，26(1):37－40.

[16]苏永华，何满潮，孙晓明.大子样岩土随机参数统计方法[J].岩土工程学报，2001，23(1):117－119.SU Yong-hua，HE Man-chao，SUN Xiao-ming.Approach on asymptotic approximations of polynomials for probability density function of geotechnics random parameters[J].Chinese Journal of Geotechnical Engineering，2001，23(1):117－119.

[17]蒋水华，冯晓波，李典庆，等.边坡可靠度分析的非侵入式随机有限元法[J].岩土力学，2013，34(8):2347－2354.JIANG Shui-hua，FENG Xiao-bo，LI Dian-qing，et al.Reliability analysis of slope using non-intrusive stochastic finite element method[J].Rock and Soil Mechanics，2013，34(8):2347－2354.

[18]蒋水华，李典庆，周创兵，等.考虑参数空间变异性的非饱和土坡可靠度分析[J].岩土力学，2014，35(9):2569－2578.JIANG Shui-hua，LI Dian-qing，ZHOU Chuang-bing，et al.Reliability analysis of unsaturated slope considering spatial variability[J].Rock and Soil Mechanics，2014，35(9):2569－2578.

[19]SILVA R S，LOPES H F.Copula，marginal distributions and model selection:a Bayesian note[J].Statistics and Computing，2008，18(3):313－320.

[20]HUARD D，ÉVIN G，FAVRE A C.Bayesian copula selection[J].Computational Statistics &Data Analysis，2006，51(2):809－822.