黏性土填料下考虑土拱效应的非极限主动土压力计算方法

娄培杰

（1.安徽理工大学 土木建筑学院，安徽 淮南 232001；2.安徽理工大学 土木工程博士后科研流动站，安徽 淮南 232001）

1 引言

现今，学者们对挡土墙土压力的影响因素有了更深入地认识与了解，包括：位移条件、位移模式以及土拱效应等。为了考虑这些因素的影响，学者们不断地进行探索，并且发展了很多的土压力计算理论[1－5]。

为了研究土体在非极限状态下的土压力，众多学者如Bang[1]、Chang[2]、蒋波[3]、卢坤林[4]、张永兴[5－6]、贾宁[7]等采用了内摩擦角发挥角的概念来对此问题进行求解，这一概念的好处在于将应用于极限状态分析的摩尔-库仑准则用于非极限状态的土力学分析中。而如何确定内摩擦角发挥角则成为一个关键性的问题，Chang[2]假设内摩擦角发挥角与位移呈线性关系，徐日庆[8]、龚慈[9]等在Chang基础上假设内摩擦角发挥角与位移呈非线性关系。施建勇等[10]从应力路径的角度给出了内摩擦角发挥角，这一方法在理论上更加合理，因而得到了多数学者们的采用[4，11]。上述研究成果仅仅适用于砂性土，徐日庆等[11]运用坐标平移法，给出了黏性土内摩擦角发挥角和黏聚力发挥值，在此基础上运用薄层微分层法给出了黏性土非极限状态土压力计算结果。但上述结果并未考虑土拱效应的影响。

土拱效应是自然界中很普遍的一种现象，其力学效应已应用于基坑[1－5]、抗拔桩承载力[12]、煤矿巷道充填[13]等方向。因而，在计算挡土墙非极限状态土压力时考虑土拱效应得到的结果会更加科学。

蒋波[3]、卢坤林[4]等对比研究了砂性土填料下考虑土拱效应和不考虑土拱效应下对非极限土压力的影响，结果表明，考虑土拱效应时其求解结果更加接近于试验结果；涂兵雄[14]、朱建明[15]等解决了黏性土土拱效应在极限状态下的主动土压力。从上述研究发展趋势来看，将土拱效应用于分析黏性土填料下非极限状态主动土压力计算理论可以进一步完善土压力计算理论。

本文基于挡土墙后填土应力路径推导的内摩擦角发挥角及黏聚力发挥值，假定土拱形状为圆弧形，给出了倾斜墙下侧向主动土压力系数的求解公式。采用微分层析法研究了倾斜墙下的层间竖向平均应力，最终得到了黏性土填料下倾斜墙非极限主动土压力系数计算理论。然后通过与已有的方法及相关室内模拟试验进行对比验证本文法的合理性，研究了相关参数如位移比η，墙土摩擦角与内摩擦角之比δ/φ，墙体倾角ε，黏聚力c 等对主动土压力分布的影响。

2 土拱效应分析

2.1 非极限装填下的土拱效应分析

如图1所示，墙后土体在非极限状态下，其土力学分析采用内摩擦角发挥角、墙土摩擦角发挥角、黏聚力发挥值，即确定不同应变约束条件下内摩擦角，墙土摩擦角，黏聚力的发挥程度。对于平动模式而言，文献[11]根据应力路径给出了上述3个参数的确定方法：

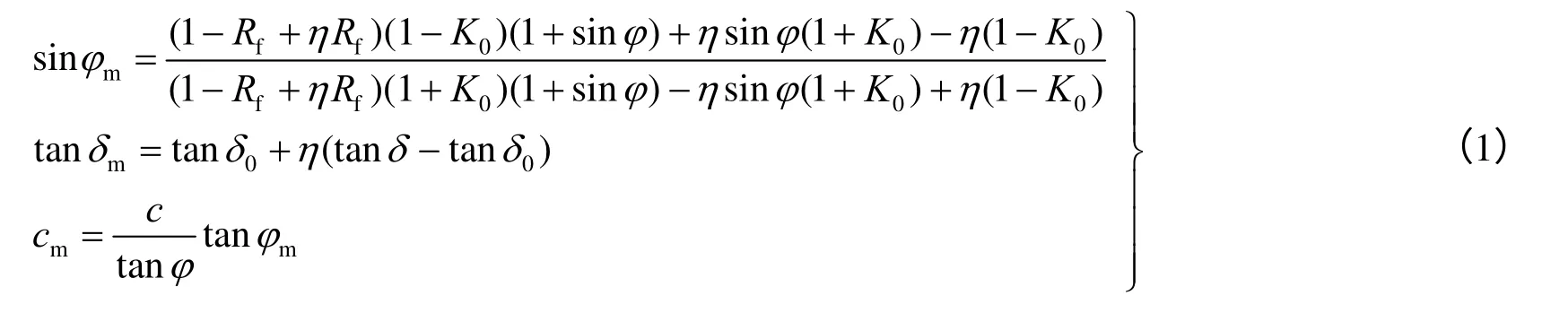
式中：cm、φm、δm为非极限状态下的黏聚力、土体内摩擦角、墙土摩擦角。Rf为破坏应力比，其取值大小在0.75～1.00之间。η为墙体土体位移的影响，其大小为η=S /Sa（S为位移，Sa为达到主动极限土压力状态的位移），当S=0时，即土体处于静止状态时，内摩擦角发挥角、墙土摩擦角发挥角取值可采用Federico等[16]的研究成果：φ0=0.64φ即K0=(1 -sin 0.64φ)/(1 +sin 0.64φ)。墙土激发角[2]采用 δ0=φ/2。

倾斜墙条件下，定义非极限状态下的侧向主动土压力系数为

式中：σw为倾斜墙法向应力；为土拱曲线上平均竖向应力。

分析黏性土的非极限状态土拱效应时，假定非极限状态下的墙土黏聚力为

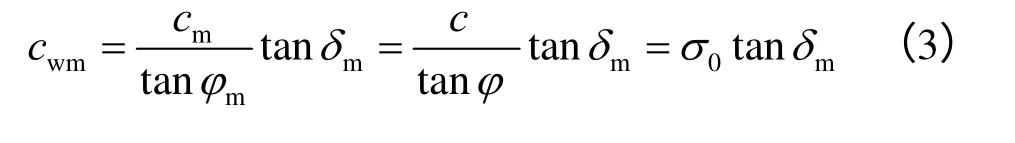
如图2所示，将纵坐标轴向右移动σ0个单位。分析倾斜墙后土体应力状态可知，σw在新坐标系为

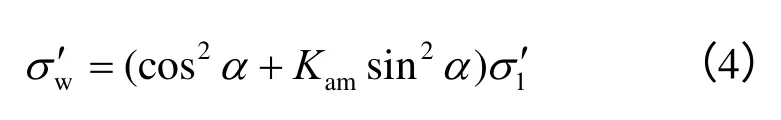
式中：Kam为朗肯主动土压力系数，大小为Kam=(1 -sin φm)/(1 +sin φm)；α为大主应力方向与墙背法向夹角，其大小为

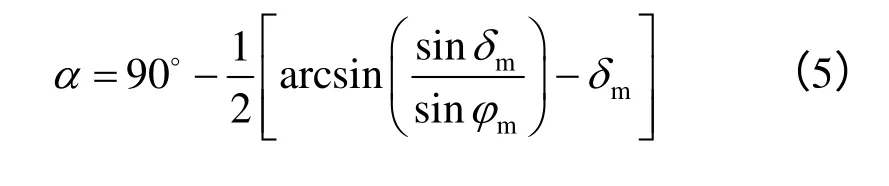
图1 挡土墙后土体应力摩尔圆Fig.1 Mohr circle for stress behind retaining wall

图2 挡土墙后土体应力摩尔圆Fig.2 Mohr circle for stress behind the retaining wall

求解竖向平均应力时，与涂兵雄等[14]一样，采用总的竖向应力除以微分层宽度：

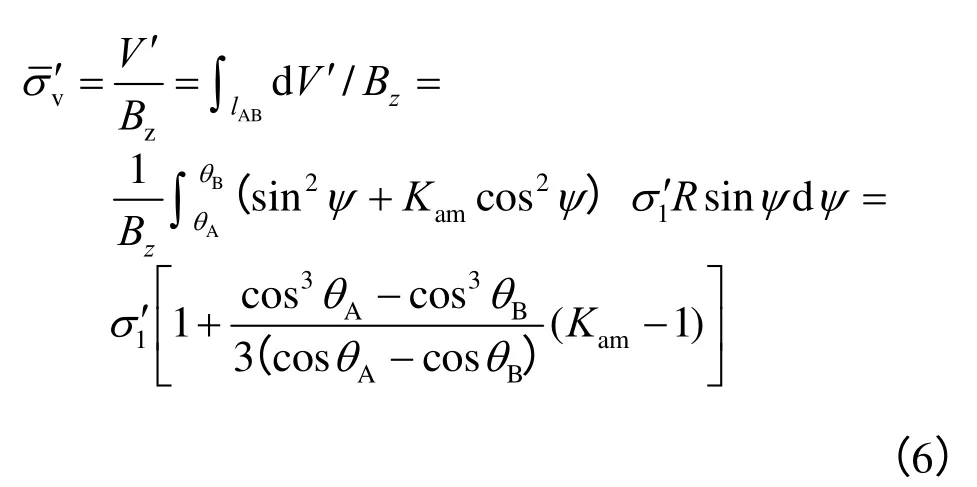
式中：θA、θB为A、B 两点的大主应力与水平向夹角。由几何关系可知，两者的大小为

式中：β为库仑滑动面倾角，可采用文献[17]的结论。由式（1）、（5）可得

2.2 主动土压力计算

图3为求解倾斜墙挡土墙的微分层单元模型。分别建立竖向及水平微分方程为

式中：Fw为倾斜墙法向作用力，大小为为倾斜墙切向作用力，大小为Fn为滑动面法向作用力，大小为Sn为滑动面切向作用力，大小为V为微分层上表面作用力，大小为F为微分层下表面作用力，大小为

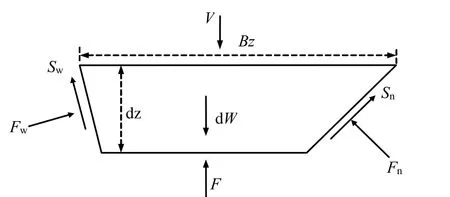
图3 水平微分层析法单元模型Fig.3 Analytical model of horizon different elements in both active pressure state and passive pressure state

为化简式（9），引入K'：

将式（10）代入式（9）可得

式中：P、Q 计算公式分别为

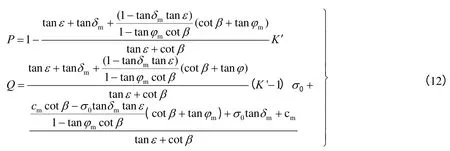
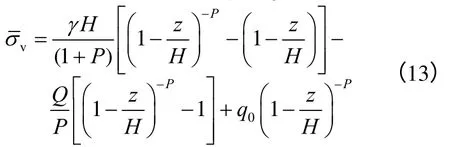
式（13）即为考虑了土拱效应的倾斜墙下的黏性土非极限状态主动土压力计算理论公式。当c=0 kPa，ε=0°时，式（13）得到的结果与文献[5]得到的结果一致。

根据式（2）的定义可知，倾斜墙后法向应力为

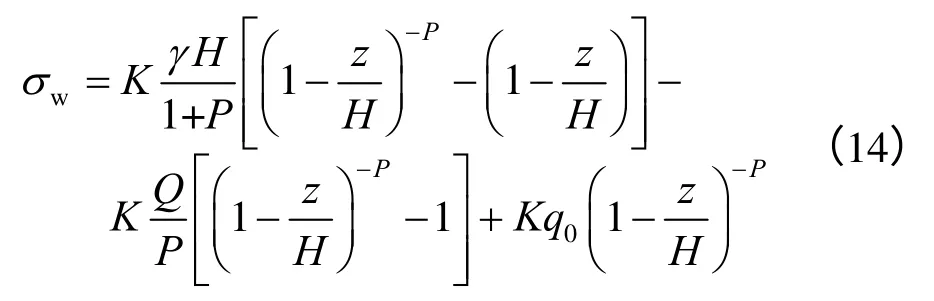
由式（14）可得，倾斜墙下非极限状态的主动土压力法向合力可表达为

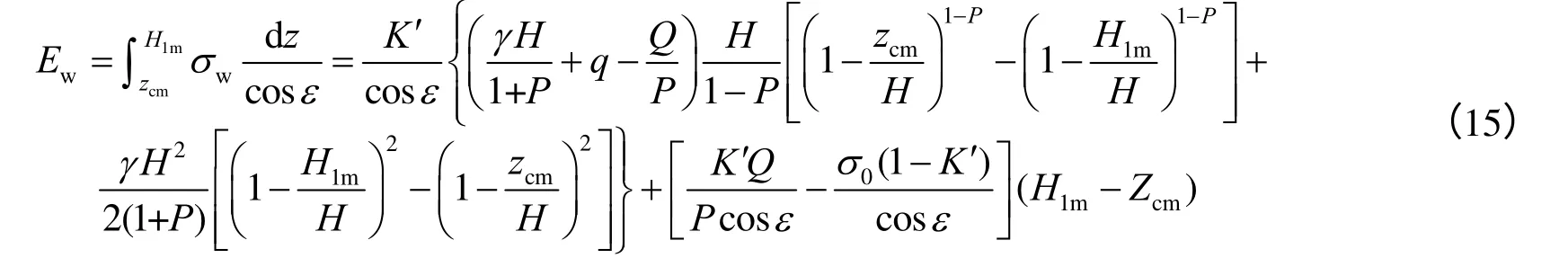
H1m为非极限状态下墙底零应力区高度，其大小通过令式（14）=0试算得到。

土压力合力为

倾覆力矩为

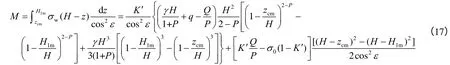
土压力作用点到墙底竖向距离为

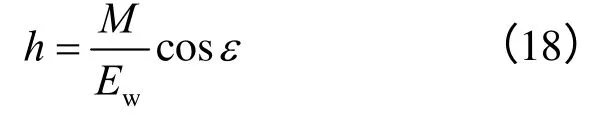
式（15）～（17）中，Zcm为非极限状态下的张拉裂缝高度，其大小可令式（8）K=0得到：

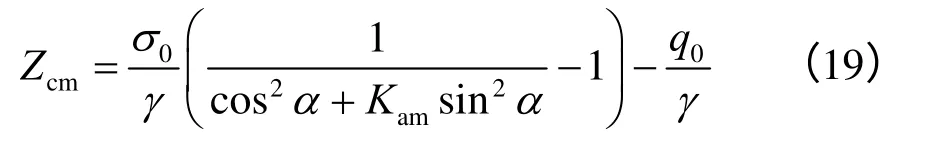
3 试验验证

3.1 周应英试验

试验条件如下[18]：模型尺寸为5.5 m（长）×2.0 m（宽）×4.5 m（高）。土样参数如下：φ=24.3°，c=1.47 kPa，γ=14.3 kN/m3，δ=0.9φ=21.4°。其他计算参数如下：ε=0°，β=51.4°，Rf=0.85，cw=1.28 kPa。静止状态下位移比η=0，平移3.9 cm时位移比η=1.0。图4及表1对比了本文法与徐日庆[11]法（不考虑土拱效应）的计算结果。由此可知，墙后填土不管是在静止状态还是在平移状态下，土压力均呈非线性分布，并且在墙底土压力会急剧减小，本文法及徐日庆法给出的规律是一致的。在静止状态下，本文法较徐日庆法计算结果更接近于试验结果。在极限主动土压力状态下，本文法与徐日庆法计算结果相差不大，均接近于试验结果。

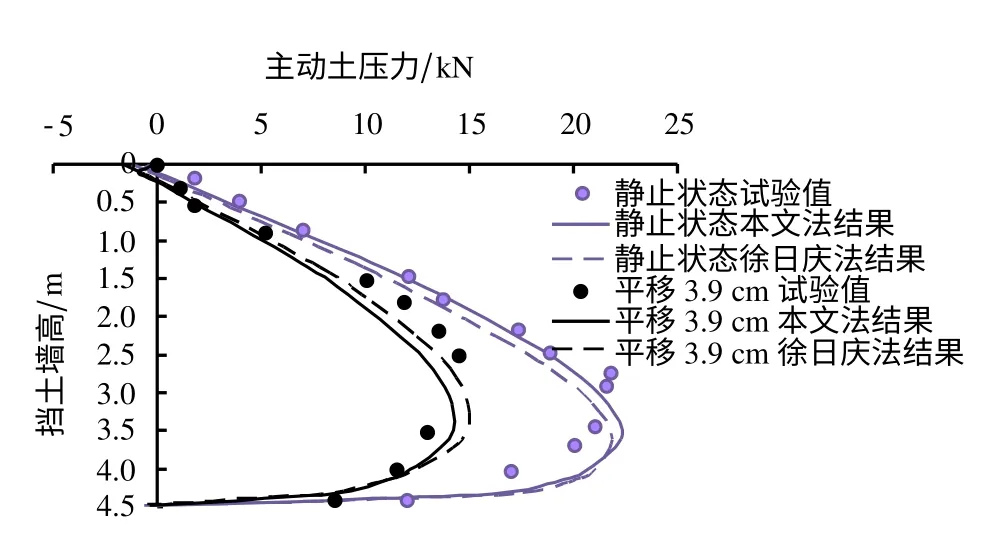
图4 挡土墙后主动土压力计算比较Fig.4 Comparison of calculated active pressure behind retaining wall based on various methods

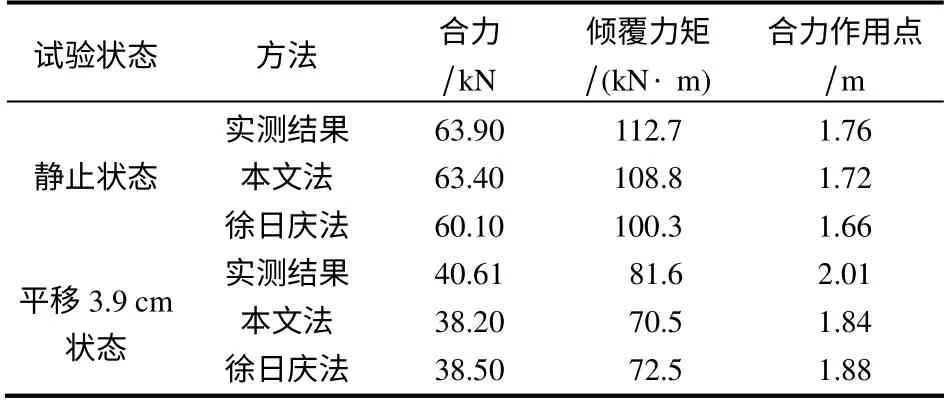
表1 试验计算结果对比Table 1 Comparison of earth pressures obtained with different methods

4 规律研究

本文重点研究了η、δ/φ、ε、c 对非极限主动土压力分布和作用点的影响，计算分析各情况下的基本参数统一取值为γ=18 kN/m3，φ=25°，c=10 kPa（在具体考虑c 值影响时另取c 值），H=10 m，Rf=0.85，其他参数在具体计算时再分别给出。

4.1 位移比η 的影响

计算参数同上，其他参数δ/φ=1.0。图5给出了倾角ε 分别取0°、10°、15°下的非极限状态主动土压力分布。随着η 的增大，主动土压力逐渐从静止土压力状态转向极限主动土压力状态，土压力分布的非线性趋势加强，土压力强度最大作用点会逐渐上移。而随着ε 的增加，土压力分布非线性强度会减弱，并且η 越小，改变会更加明显，这点也说明土拱效应在极限状态下的影响较非极限状态的影响大。

图6给出η 对土压力合力作用点的影响，随着η 的增大，土压力作用点呈先下降后上升的趋势，这是与砂性土不同的地方，其原因可能是因为上部张拉裂缝的影响。但总体土压力作用点呈上升趋势，说明土拱效应的影响随着η 的增大而增强，并且这种影响随着ε 的增加会减弱。

图5 η 对挡土墙后主动土压力分布影响Fig.5 Effect of η on the active earth pressure distribution

4.2 δ/φ 的影响

计算参数同上，其他参数η=1.0。图7为ε 分别取0°、5°、10°下的δ/φ 对主动土压力的影响。随着δ/φ 的增加，土拱效应逐渐增强，土压力非线性分布逐渐增强。由图8可知，土压力作用点随着δ/φ 的增加而上升，随着ε 的增大而下降。对比η 取1.0、0.5两种状态下土压力作用点的变化规律，表明δ/φ 的影响随着η 的增加而增加。

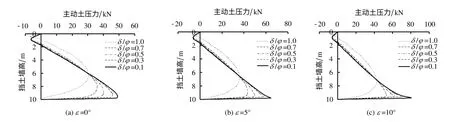
图7 δ/φ 对挡土墙后主动土压力分布影响Fig.7 Effect of δ/φ on the active earth pressure distribution

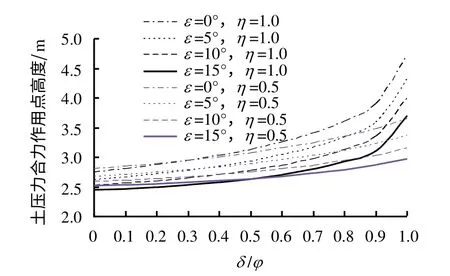
图8 δ/φ 对主动土压力合力作用点的影响Fig.8 Effect of δ/φ on the acting point of the active earth pressure resultant

4.3 ε 的影响

本节的计算参数同上，其他参数η=1.0，δ/φ=1.0。图9的计算结果表明，随着ε 的增大，土压力非线性强度趋势逐渐减弱，土压力强度最大作用点逐渐下降。图10为ε 对土压力合力作用点高度的影响，其计算参数除δ/φ、η为图中所示外，其余参数与图9参数一致，结果表明，ε 越大，土压力作用点高度降低，即挡土墙越倾斜，墙后土体的土拱作用影响越小。

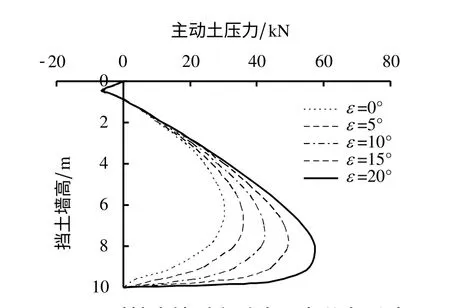
图9 ε 对挡土墙后主动土压力分布影响Fig.9 Effect of ε on the active earth pressure distribution

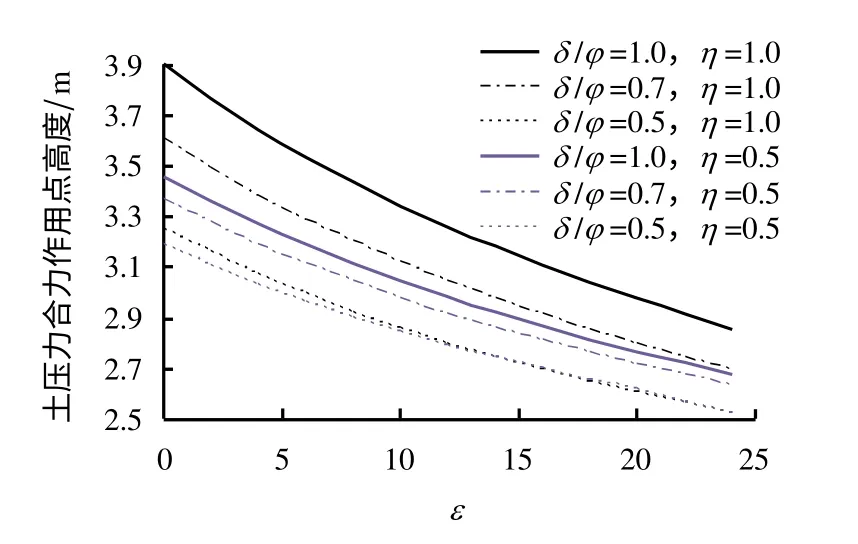
图10 ε 对主动土压力合力作用点的影响Fig.10 Effect of ε on the acting point of the active pressure resultant

4.4 c 的影响

本节的计算参数同上，其他参数δ/φ=2/3，η=1.0，ε=0°。由图11可知，随着c 的增加，主动土压力逐渐减小。

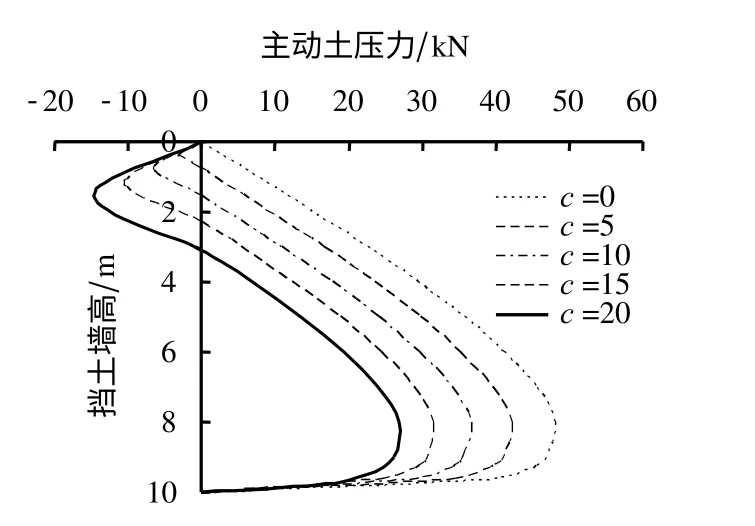
图11 c 对挡土墙后主动土压力分布影响Fig.11 Effect of c on the active earth pressure distribution

图12则研究了c 对土压力作用点高度的影响，其计算参数除ε、η为图中所示外，其余参数与图11参数一致。结果表明：随着黏聚力的增加，土压力合力作用点均呈下降趋势。并且η 越大，c 的影响越小。

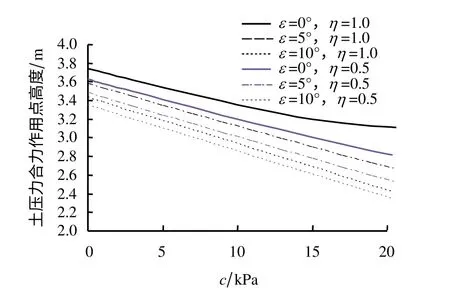
图12 c 对主动土压力合力作用点的影响Fig.12 Effect of c on the acting point of the active pressure resultant

5 结论

（1）给出了考虑土拱效应的非极限主动土压力计算公式。通过与室内相似试验及其他理论进行对比，本文方法的合理性得到了验证。

（2）研究了非极限主动土压力变化规律，研究了各参数如位移比η、墙土摩擦角与内摩擦角之比δ/φ、墙体倾角ε、黏聚力c 对主动土压力分布及其作用点高度的影响。

（3）土体由静止状态向极限主动土压力状态发展时，土拱效应对土压力的影响总体趋势是增大，土压力合力作用点高度会上升。对于黏性土而言，与砂性土不同，土压力合力作用点可能会呈现先下降后上升的规律，这与上部张拉裂缝的发展可能有较大关系。

（4）墙土摩擦角与内摩擦角δ/φ 对土压力分布有较大的影响。随着δ/φ 的增大，土压力分布曲线非线性强度会增强，土压力合力作用点高度上升。并且，δ/φ 的影响会随着位移比η的增大而增大。

（5）挡土墙倾斜角度越大，得到的主动土压力非线性强度越小，合力作用点高度越低即土拱效应对非极限主动土压力的影响越小。

（6）墙后土体填料黏聚力越大，土压力合力作用点呈下降趋势。并且，土体越接近于极限主动土压力状态，黏聚力c 对土压力的影响越小。

（7）本文给出的土拱效应分析思路同样适用于煤矿巷道采空区充填，管涵回填等土压力计算分析。

[1]BANG SANGCHUL.Active earth pressure behind retainingwalls[J].JournalofGeotechnical Engineering，1985，111(3):407－412.

[2]CHANG M F.Lateral earth pressure behind rotating wall[J].Canadian Geotechnical Journal，1997，34(2):498－509.

[3]蒋波，应宏伟，谢康和，等.平动模式下挡土墙非极限状态主动土压力计算[J].中国公路学报，2005，18(2):24－27.JIANG Bo，YING Hong-wei，XIE Kang-he，et al.Computation of active earth pressure under non-limit state for retaining wall with mode of translation[J].China Journal of Highway and Transport，2005，18(2):24－27.

[4]卢坤林，朱大勇，杨扬.考虑土拱效应的非极限主动土压力计算方法[J].中国公路学报，2010，23(1):19－25.LU Kun-lin，ZHU Da-yong，YANG Yang.Calculation method of active earth pressure under non-limit state considering soil arching effects[J].China Journal of Highway and Transport，2010，23(1):19－25.

[5]张永兴，陈林.挡土墙非极限状态主动土压力分布[J].土木工程学报，2011，44(4):112－119.ZHANG Yong-xing CHEN Lin.Active earth pressure on retaining walls in non-limit state[J].China Civil Engineering Journal，2011，44(4):112－119.

[6]胡俊强，张永兴，陈林，等.非极限状态挡土墙主动土压力研究[J].岩土工程学报，2013，35(2):381－387.HU Jun-qiang，ZHANG Yong-xing，CHEN Lin，et al.Active earth pressure on retaining wall under non-limit state[J].Chinese Journal of Geotechnical Engineering，2013，35(2):381－387.

[7]贾宁.有限填土静止土压力系数计算方法研究[J].岩土工程学报，2012，34(7):1333－1337.JIA Ning.Coefficient of at-rest earth pressure from limited backfill[J].Chinese Journal of Geotechnical Engineering，2012，34(7):1333－1337.

[8]徐日庆，龚慈，魏纲，等.考虑平动位移效应的刚性挡土墙土压力理论[J].浙江大学学报(工学版)，2005，39(1):119－122.XU Ri-qing，GONG Ci，WEI Gang，et al.Theory of earth pressure against rigid retaining walls considering translational movement effect[J].Journal of Zhejiang University(Engineering Science)，2005，39(1):119－122.

[9]龚慈，魏纲，徐日庆.RT模式下刚性挡墙土压力计算方法研究[J].岩土力学，2006，27(9):1588－1592.GONG Ci，WEI Gang，XU Ri-qing.Earth pressure against rigid retaining wall rotating about top[J].Rock and Soil Mechanics，2006，27(9):1588－1592.

[10]施建勇，雷国辉，艾英钵，等.土压力变化规律的应力路径三轴试验研究[J].岩土力学，2005，26(11):1700－1704.SHI Jian-yong，LEI Guo-hui，AI Ying-bo，et al.Stress path controlled triaxial experimental study of lateral earth pressure behavior[J].Rock and Soil Mechanics，2005，26(11):1700－1704.

[11]徐日庆，廖斌，吴渐，等.黏性土的非极限主动土压力计算方法研究[J].岩土力学，2013，34(1):148－154.XU Ri-qing，LIAO Bin，WU Jian，et al.Computational method for active earth pressure of cohesive soil under nonlimit state[J].Rock and Soil Mechanics，2013，34(1):148－154.

[12]TING C H，SHUKLA S K，SIVAKUGAN N.Arching in soils applied to inclined mine stopes[J].International Journal of Geomechanics，2011，11(1):29－35.

[13]SHELKE A，PATRA N R.Effect of arching on uplift capacity of pile groups in sand[J].International Journal of Geomechanics，2008，8(6):347－354.

[14]涂兵雄，贾金青.考虑土拱效应的黏性填土挡土墙主动土压力研究[J].岩石力学与工程学报，2012，31(5):1064－1070.TU Bing-xiong，JIA Jin-qing.Research on active earth pressure behind rigid retaining wall from clayey backfill considering soil arching effects[J].Chinese Journal of Rock Mechanics and Engineering，2012，31(5):1064－1070.

[15]朱建明，赵琦，郑雨婷.对“考虑土拱效应的黏性填土挡土墙主动土压力研究”的讨论[J].岩石力学与工程学报，2013，32(5):1073－1075.ZHU Jian-ming，ZHAO Qi，ZHENG Yu-ting.Discussion on“ research on active earth pressure behind rigid retaining wall from clayey backfill considering soil arching effects”[J].Chinese Journal of Rock Mechanics and Engineering，2013，32(5):1073－1075.

[16]FEDERICO A，ELIA G，GERMANO V.A short note on the earth pressure and mobilized angle of internal friction in one-dimensional compression of soils[J].Journal of Geo Engineering，2008，3(1):41－46.

[17]GRECO VENANZIO R.Discussion of“active earth pressure on retaining wall for c-φ soil backfill under seismic loading condition”by S.K.Shukla，S.K.Gupta，and N.Sivakugan[J].Journal of Geotechnical and Geoenvironmental Engineering，2010，136:1583－1584.

[18]周应英，任美龙.刚性挡土墙主动土压力的试验研究[J].岩土工程学报，1990，12(2):19－26.ZHOU Ying-ying，REN Mei-long.An experiment study on active earth pressure behind rigid retaining wall[J].Chinese Journal of Geotechnical Engineering，1990，12(2):19－26.