Fibonacci数列一类推广数列的性质与应用

文/黄秋茂

(作者单位：汕头市潮阳建筑职业技术学校)

Fibonacci数列一类推广数列的性质与应用

文/黄秋茂

使用矩阵的方法，对Fibonacci数列的一类推广数列{fn}进行深入的讨论，得到它的矩阵，并得到相应的性质，同时也涉及了这类数列的一些应用问题。

Fibonacci数列;通项公式;矩阵

主要内容

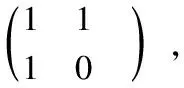
矩阵表示形式:

行列式形式:

随着人们对Fibonacci数列的深入研究，Fibonacci数列的推广形式也进一步丰富起来，如彭黎霞的《三阶Fibonacci数列的性质与应用》，就通过对三阶Fibonacci数列的分析，求得通项公式，并得到一些性质，同时举例加以应用。本文利用高等代数的方法，对Fibonacci数列的推广数列{fn}进行定义，即f0=1,f1=1,f2=1,,当n≥2时,fn+1=fn+fn-2，同时求得相应的矩阵，并得到与Fibonacci数列相似的性质，并举例加以应用。

1.fn+1=fn+fn-2数列与fn+1=fn+fn-2矩阵

定义1数列{fn},f0=1,f1=1,f2=1,fn+1=fn+fn-2,n=2,3,4….称数列{fn}为Fibonacci数列的推广数列.

定理1对于{fn},有

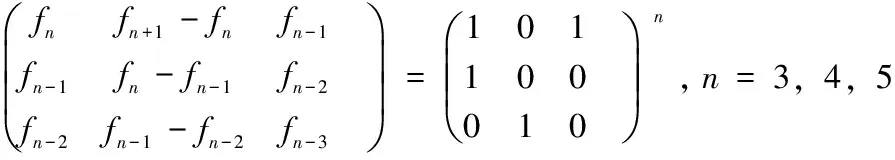
证:当n=3时,

等式成立.

假设当n=k时,等式成立.即

当n=k+1时,

即等式成立.

综上所述,对于一切大于或等于3的正整数n都成立.证毕.

2.Fibonacci数列一类推广数列{fn}中的性质

性质1 对于{fn}中三个连续的数,它们的最大公因子为1.即(fn+2,fn+1,fn)=1

证由推论1得

将它们按第一列展开得:

设(fn+2,fn+1,fn)=d,则有d=1,即(fn+2,fn+1,fn)=1.

3.数列{fn}通项的组合数和形式

设爬n阶楼梯,一次可跨三阶或一阶,爬到n阶时不同的方法有多少种?

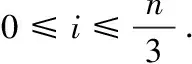
即得.

定理4 对于Fibonacci数列一类推广数列{fn},有

4.数列{fn}在组合上的应用

例1有雌雄一对兔子,假定过三个月后,每个月便可繁殖雌雄各一的一对小兔子,小兔子经过三个月后,每一对兔子每个月也能繁殖雌雄各一的一对小兔子.问过n个月后共有多少对兔子?

分析:设第n个月底,共有F(n)对兔子.易知F(1)=1,F(2)=1,F(3)=2.当n≥4时,第F(n)个月底,共有F(n)对兔子,他们可分成如下两类:①在第n-1个月或以前出生的兔子.属于此类的兔子共有F(n-1)对.②在第n个月出生的兔子.属于此类的兔子是由第n-3个月底的F(n-3)对兔子的繁殖.故共有F(n-3)对兔子.由加法原则,有F(n)=F(n-1)+F(n-3).

例2现有红蓝两种颜色的小球(两种小球的数量都足够多)，将其排成一行，要求每个蓝球的后面至少有两个红球，假设一行有n个位置，问满足条件的排法有多少种。

分析：设共有f(n)种不同的排法。当n=1时，这时只有一个位置，这时只能放红球，蓝球不满足要求，这时只有一种排法，可得f(1)=1；当n=2时，这时有两个位置，但只能放两个红球，蓝球放在任何一个位置都不合适，这时只有一种排法，可得f(2)=1；当n>2时，这时有三个或更多的位置，如果第一个位置放置红球，则后面的n-1个位置只要按要求排放即可，有f(n-1)中排法，如果第一个位置放蓝球，根据要求后面两个位置只能放红球，则后面n-3个位置有f(n-3)种排法，综合起来有f(n)=f(n-1)+f(n-3)，且f(1)=1，f(2)=1，即排法f(n)构成Fibonacci数列。

例3某社团社长要把某个通知传达下去，他决定在QQ上把通知传达出去(不考虑群发)，他把这则通知发给两个社员，两位社员收到消息后也立即转发给其他人，假设两位部长每人转发通知两次，其他人收到通知后也会同样转发两次，同时假设这中间没有重复现象出现，发送和转发一次需要1秒钟，并且转发后需要隔一秒钟才能再转发一次，则10秒钟后，有多少人收到通知？

分析:根据题意可知，第一秒钟，社长发送通知，第二秒钟有一个部长接到通知，到了第三秒钟，共有两个人新接到通知，第四秒钟就有1+2=3人接到通知，第五秒钟发布社长已经通知了两个部长就不再通知其他人了，此时接到通知的人有1+3=4人，依次类推，到了第n秒钟，接到通知的人数刚好是前一秒钟接到通知人数与前三秒钟接到通知人数的总和，如此则刚好构成Fibonacci数列，则有10秒钟后接到通知的人数是f0+f1+f2+…+f10=87。

(作者单位：汕头市潮阳建筑职业技术学校)

[1]吴振奎.斐波那锲数列[M].沈阳:辽宁教育出版社,1987

[2]邵品琮.广义Fibonacci序列及其应用[J].青岛教育学院报,2001,14(1):36-38

[3]及万会.r阶Fibonacci数列[J].高师理科学刊,2005,25(1):13-16.

[4]彭黎霞.三阶Fibonacci数列的性质与应用[J].莆田学院学报,2006,13(5):5-8

[5]曹汝成.组合数学[M].广州:华南理工大学出版社,2001.

黄秋茂，汉，汕头市潮阳建筑职业技术学校，助理讲师，学历：本科。

O611.4

：A

：2095-9214(2015)03-0132-02