应用R软件metafor程序包实现轮廓增强漏斗图

魏雪梅，胡定伟，敬媛媛，张超，张永刚，曾宪涛

• 循证理论与实践 • 论著 •

应用R软件metafor程序包实现轮廓增强漏斗图

魏雪梅，胡定伟，敬媛媛，张超，张永刚，曾宪涛

目的介绍轮廓增强漏斗图应用R软件metafor程序包的实现方法及其作用。方法通过实例展示应用“funnel( )”函数绘制传统漏斗图和轮廓增强漏斗图的方法，并进行比较分析。结果R软件metafor程序包能够实现普通的轮廓增强漏斗图和结合剪补法的轮廓增强漏斗图。相对于传统漏斗图，轮廓增强漏斗图对对称性的识别更为敏感，且能识别纳入研究分布在有无统计学意义的区域。结论轮廓增强漏斗图利于判断漏斗图是否真正不对称以及这种不对称是否由发表偏倚所致。

发表偏倚；Meta分析；轮廓增强漏斗图；R软件；metafor程序包

Meta分析（meta-analysis）是一种定量综合多个同类研究效应的定性研究方法[1]，广泛应用于医学、教育、经济、犯罪、心理学等领域，其结论是否可信和有价值取决于在制作时是否能够客观、全面地评价分析研究过程中的各种偏倚。Meta分析的偏倚是指制作Meta分析过程中产生的偏倚。《Cochrane Handbook for Systematic Reviews of Interventions》5.0及以上版本中认为Meta分析中纳入研究的完整性主要通过报告偏倚来衡量，并将报告偏倚分成了7类：发表偏倚、时滞偏倚、多重/重复发表偏倚、发表位置偏倚、引用偏倚、语言偏倚和结果报告偏倚[2]。

这些偏倚中，最受关注和研究最多的为发表偏倚。发表偏倚是指由研究结果的性质和方向导致研究成果的发表与未发表造成的偏倚，目前评价的方法有很多种，最常用的是漏斗图法（funnel plot）[2,3]。一般认为，若漏斗图不对称或对称性差则认为存在发表偏倚。但引起漏斗图不对称的原因除发表偏倚外，还有引用偏倚、真实的异质性、（重复）发表偏倚、选择性偏倚、语言偏倚等[2,3]。传统的漏斗图不能鉴别不对称的原因，因此Peter及其同事在2008年研发了一种改良的方法用以鉴别漏斗图不对称是否由发表偏倚所引起，即轮廓增强漏斗图法（contour-enhanced funnel plot）[4]。当前，已有文章介绍应用R软件meta程序包实现[5]，本文介绍如何使用R软件metafor程序包实现。

1资料和方法

1.1 资料来源本文以《Efficacy of BCG vaccine in the prevention of tuberculosis. Meta-analysis of the published literature》文中[6]的数据（表1）为例进行演示，该Meta分析是探讨BCG对结核病的疗效，纳入研究间存在异质性。将表1中的数据使用Excel 2007命名为“bcg.xlsx”存储在C盘，以备加载。

1.2 程序包安装与加载本文使用R软件的版本为R 3.1.2版，R的下载及安装见《R软件Metafor程序包在Meta分析中的应用》一文[7]。

R安装完成后，通过下述命令安装与加载metafor程序包：

install.packages("metafor")

library(metafor)

此外，因为数据存取格式为“.xlsx”，故还需同时安装与加载对应的程序包：

install.packages("xlsx ")

library(xlsx)

1.3 加载数据与模型拟合与meta程序包不同，metafor程序包模型拟合的方法有两种：一是在采用“escalc( )”函数计算出效应量及其方差后进行拟合运算，二是直接采用原始数据进行模型的拟合运算。本文采用直接拟合的方式。

首先，采用下述命令进行数据的读取：

bcg＜-read.xlsx("c:/bcg.xlsx", 1)

bcg

第一行命令中的“1”表示是读取的excel表格的“Sheet1”。

接着，以RR为效应量，使用“rma( )”函数基于随机效应模型（因具有异质性）进行拟合，命令如下：

res＜-rma(measure="RR", ai=a, bi=b, ci=c, di=d, data=bcg, method="REML")

res

1.4 图形绘制方法首先，使用“funnel( )”函数绘制传统漏斗图。命令为：

funnel(res, main="Funnel Plot")

接着，在传统漏斗图的基础上添加相关的参数进行限定以绘制轮廓增强漏斗图。具体命令如下：

funnel(res, level=c(90, 95, 99), shade=c("white", "gray", "darkgray"), refline=0, atransf=exp, at=log(c(.10, .25, .5, 1, 2, 4, 10)))

legend(1, 0.02, c("0.1 ＞ p ＞ 0.05", "0.05 ＞ p ＞0.01", "＜ 0.01"), fill=c("white", "gray", "darkgray"))

par(mfrow=c(2, 2))

第三，联合实现剪补法[2,3,8]的“trimfill( )”函数绘制剪补后的轮廓增强漏斗图。命令如下：

trf＜-trimfill(res)

funnel(trf, level=c(90, 95, 99), shade=c("white", "gray", "darkgray"), refline=0, atransf=exp, at=log(c(.10, .25, .5, 1, 2, 4, 10)))

legend(1, 0.02, c("0.1 ＞ p ＞ 0.05", "0.05 ＞ p ＞0.01", "＜ 0.01"), fill=c("white", "gray", "darkgray"))

par(mfrow=c(2, 2))

2 结果

2.1 传统漏斗图传统漏斗图，从图来看，图形左右对称性好，因此可能不存在发表偏倚。使用Egger线性回归法[2,3,9]的结果也表明不存在发表偏倚（P=0.4218）（图1）。

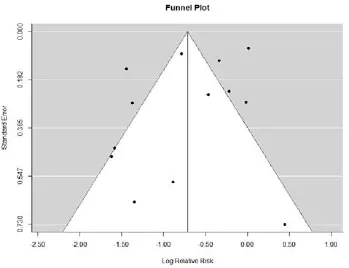
图1 传统漏斗图

2.2 轮廓增强漏斗图轮廓增强漏斗图，该图从统计学99%、95%和90%三个水平层面进行检测。从图2可看出，研究左右分布不均，主要分布在左侧，5项研究分布在无统计学意义区域中（白色区域），表明可能存在发表偏倚（图2）。

2.3 剪补后的轮廓增强漏斗图剪补后的轮廓增强漏斗图，由图可知，需要再增补一项研究（图中虚心圆圈）可以纠正漏斗图的不对称；但增补的该项研究仍旧分布在无统计学意义区域（白色区域），表明存在不具有统计学意义的研究未发表。因此，可以表明本Meta分析存在一定程度的发表偏倚（图3）。

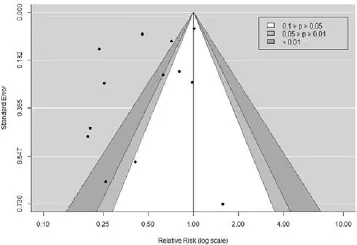
图2 轮廓增强漏斗图

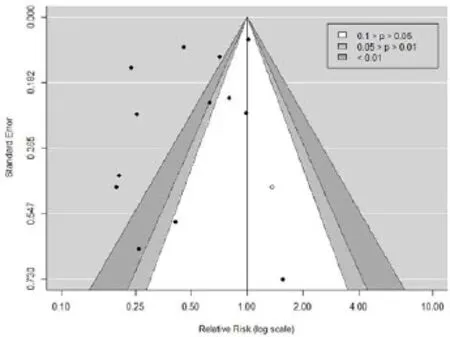
图3 剪补后的轮廓增强漏斗图

3 讨论

漏斗图是定性测量发表偏倚的常用方法，它是将单个研究的效应量（或其对数）作横轴，标准误（研究规模）作纵轴所作的散点图[2-4]。由于漏斗图所基于的假设是效应量的精度随着样本量的增加而增加，因此样本量小的研究，精度低，分布在漏斗图的底部，且向周围分散；样本量大的研究，精度高，分布在漏斗图的顶部，且向中间集中；如果没有偏倚的存在时，散点形成一个对称的倒置漏斗型，故此得名。如果存在偏倚，例如因为没有统计学意义的小样本试验没被发表，这将导致在漏斗图的底部出现一个角落的缺失而表现为不对称[2,3,10]。

然而，除发表偏倚外，其它导致漏斗图不对称的原因有：①低质量小样本试验，包括方法学设计差、分析不充分及造假；②真实的异质性，即因研究尺度不同导致效应量的差异（例如，因为研究尺度不同而导致干预措施的强度不同或潜在危险因素不同）；③假象；④机遇[2,3]。因此，单纯从漏斗图对称与否判断是否存在发票偏倚是不太准确的[3,10]。

传统的漏斗图只能判断纳入研究分布的范围，不能判断哪些研究落在无统计学意义的区域；即便是结合了剪补法的漏斗图亦无法判断。因此，需要一种新的、更为准确的方法判断漏斗图的不对称到底是否是由发表偏倚所引起。轮廓增强漏斗图就这样应运而生了[3-5]。

轮廓增强漏斗图的绘制方法与传统漏斗图相似，只是在传统漏斗图的基础上分为3个水平增加了识别统计学差异的区域。从而利于判断是否真正的对称或不对称，以及哪些研究分布在无统计学意义区域。若存在不对称，那么则建议结合剪补法进一步判断需要增补的研究分布在具有统计学意义的区域还是不具有统计学意义的区域。若增补的研究分布在无统计学意义的区域，表明存在无统计学意义的研究未行发表，从而说明漏斗图的不对称是由发表偏倚所致，即存在发表偏倚；反之，若分布在具有统计学意义的区域，则表明不对称不是由发表偏倚所致，也即不存在发表偏倚[4,5]。

从本文结果看，传统漏斗图对称性较好，且Egger线性回归检验[2,3,9]亦表明不存在发表偏倚。然而，轮廓增强漏斗图显示对称性较差，可能存在发表偏倚；进一步结合剪补法，表明需要增补的一项研究分布在无统计学意义区域，即本Meta分析很可能存在发表偏倚。因此建议作者若使用的是R、Stata或SAS软件制作Meta分析时[11]，能够绘制轮廓增强漏斗图来明确是否存在发表偏倚。

需要说明的是，任何一种方法都具有其局限性，轮廓增强漏斗图法也不例外。此外，就算R软件的不同程序包，给出的结果也不一定相同；本例若使用Meta程序包[5]，则所需增补的4项研究全部分布在具有统计学意义的区域，表明不存在发表偏倚。因此，需要制作者根据实际情况综合考虑选用，并根据Meta分析的主题结合专业背景做出合理的解读、讨论与给出相关的启示。

[1] 曾宪涛,冷卫东,郭毅,等. Meta分析系列之一: Meta分析的类型[J].中国循证心血管医学杂志,2012,4(1):3-5.

[2] Higgins JPT,Green S (editors). Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0[updated March 2011]. The Cochrane Collaboration,2011,Available from www.cochranehandbook.org.

[3] 罗杰,冷卫东. 系统评价/Meta分析理论与实践[M]. 北京:军事医学科学出版社,2013.

[4] Peters JL,Sutton AJ,Jones DR,et al. Contour-enhanced meta-analysis funnel plots help distinguish publication bias from other causes of asymmetry[J]. J Clin Epidemiol,2008, 61(10):991-6.

[5] 张天嵩,熊茜,袁婷. 附加轮廓线漏斗图的绘制在R软件中的实现[J]. 循证医学,2013,13(5):307-13.

[6] Colditz GA,Brewer TF,Berkey CS,et al. Efficacy of BCG vaccine in the prevention of tuberculosis. Meta-analysis of the published literature[J]. JAMA,1994,271(9):698-702.

[7] 董圣杰,曾宪涛,郭毅. R软件Metafor程序包在Meta分析中的应用[J]. 中国循证医学杂志,2012,12(9):1141-7.

[8] Duval S,Tweedie R. Trim and fill:A simple funnel-plot-based method of testing and adjusting for publication bias in meta-analysis[J]. Biometrics,2000,56(2):455-63.

[9] Egger M,Davey Smith G,Schneider M,et al. Bias in meta-analysis detected by a simple, graphical test[J]. BMJ,1997,315(7109):629-34.

[10]Peters JL,Sutton AJ,Jones DR,et al. Comparison of two methods to detect publication bias in meta-analysis[J]. JAMA,2006,295(6):676-80.

[11] 曾宪涛,田国祥,张超,等. Meta分析系列之十五:Meta分析的进展与思考[J]. 中国循证心血管医学杂志,2013,5(6):561-87.

Application contour-enhanced funnel plot using metafor package in R

WEI Xue-Mei*, HU Ding-Wei, JING Yuan-Yuan, ZHANG Chao, ZHANG Yong-Gang, ZENG Xian-Tao*Nursing Department, Affiliated Hospital of North Sichuan Medical College, Nanchong 637000, Sichuan, China.

ZENG Xian-Tao, E-mail: zengxiantao1128@163.com

ObjectiveTo introduce the function of the contour-enhanced funnel plot and how to implement it using metafor package inR. MethodsWe introduced the implementation method based on the "funnel( )" function using a example. Then we compared the results of contour-enhanced funnel plot and traditional funnel plot.ResultsThe metafor package can finish the common contour-enhanced funnel plot and combine with trim and fill method. Relative to traditional funnel plot, the contour-enhanced funnel plot is more sensitivity and it can also distinguish the statistic distributions of included studies.ConclusionsThe contour-enhanced funnel plot can further to detect the symmetry or asymmetry is true and help to investigate whether the asymmetry is caused by publication bias.

Publication bias; Meta-analysis; Contour-enhanced funnel plot; R software; metafor package

R3

A

1674-4055(2015)03-0289-04

2015-02-13）

（责任编辑：姚雪莉）

国家自然科学基金青年项目(81403276);四川省卫生厅2013年度科研项目(130351);四川省教育厅2013年度课题;武汉大学“985”工程建设项目2014-2015年度专项资金

637000 四川,南充川北医学院附属医院护理部(魏雪梅,胡定伟);川北医学院预防医学系(敬媛媛);湖北医药学院附属太和医院循证医学与临床研究中心(张超,曾宪涛);四川大学华西医院中国循证医学中心(张永刚,曾宪涛);武汉大学中南医院循证与转化医学中心(曾宪涛)

曾宪涛,E-mail:zengxiantao1128@163.com

10.3969/j.1674-4055.2015.03.01