西安地区地裂缝带Q3原状黄土流变特性试验研究

邓亚虹 ，李 丽 ，慕焕东 ，王 鹏，李飞霞

（1.长安大学 地质工程系，陕西 西安 710054；2.长安大学 国土资源部岩土工程开放研究实验室，陕西 西安 710054；3.长安大学 西部矿产资源与地质工程教育部重点实验室，陕西 西安 710054；4.甘肃省交通科学研究院有限公司，甘肃 兰州 730050；5.甘肃省地矿局第三地质矿产勘查院，甘肃 兰州 730050）

1 引 言

地裂缝是一种危害严重的地质灾害，在世界上许多国家普遍存在，尤以我国和美国最为严重。自20 世纪中、后期以来，我国的汾渭盆地已有56 个县市、170 处发现地裂缝，总计约400 条，已成为我国乃至全世界地裂缝灾害最为发育、灾害最为严重的地区之一。而西安是汾渭盆地中地裂缝发育最具典型代表的地区，也是遭受地裂缝灾害最为严重的城市[1-3]。目前西安地裂缝造成的经济损失已超过50 亿，严重制约着城市的规划和发展。

目前，对地裂缝成因机制的研究已趋于成熟。美国是开展地裂缝研究最早的国家，构造成因观提出者Leonard[4]认为，地裂缝及地面破裂与附近的地震活动有关。Lofgren[5-6]用竖向和横向渗透应力解释了地面变形和地裂缝的形成。综合成因的提出者Holzer[7]认为，构造条件和开采地下水是影响地裂缝形成和活动的两个主要因素。我国对地裂缝的研究主要是以张家明的构造成因说[2]、易学发的水成说[8]以及刘国昌、彭建兵等的综合成因说[9-10]为代表。土流变特性的研究也早已开始，在Тердаги 著的《土力学原理》[11]一书中所列黏土的长期试验数据表明，黏土表现出明显的弹性后效特性。土的蠕变本构是以室内流变试验为基础，得到土体应力-应变随时间的变化规律，可以定量表征土体的流变特性。对黄土蠕变本构的研究是土流变力学理论中最基本也是最重要的组成部分，其选取原则是在能反映黄土流变规律的前提下尽量选择最简单的模型。最常用的模型形式就是元件模型，既直观、简单，又能全面反映流变介质的各种流变特性。如夏才初等[12-14]提出了统一流变力学模型，涵盖了介质的所有流变性态。王艳婷[15]用五元件广义的Kelvin 模型描述Q2黄土的黏弹性特性。李良权等[16]提出了一维、三维非线性黏弹塑性蠕变模型。但与地裂缝的流变特性相关的研究则几乎处于空白状态，考虑到汾渭盆地地裂缝多发育于黄土介质中，探索隐伏地裂缝的破裂扩展模式就必须考虑到黄土介质的力学特性，这就需要通过室内试验手段来实现。已有大型物理模型试验和数值模拟结果均显示隐伏地裂缝的破裂扩展具有反倾特征，与实际地裂缝剖面结构揭示的倾向一致性不符[17-18]。而地裂缝又是一种缓变型地质灾害，考虑其发育介质的流变特性，通过室内蠕变试验方法来探索隐伏地裂缝的破裂扩展模式及其力学机制应该是更为合理的途径。

本文以西安地区长安地裂缝（fc1）带Q3原状黄土为研究对象，采用分级加、卸载方式进行室内三轴流变试验，得到了不同围压下地裂缝带Q3原状黄土的蠕变曲线及应变速率与时间关系曲线。并基于统一流变力学模型理论，分析了不同围压、不同应力水平下的蠕变曲线特征，建立了能够全面描述各流变性态的三维蠕变本构模型，对模型及参数进行辨识，并建立了相应的三维蠕变本构方程。

2 试验方案

试验所用Q3原状黄土取自西安地区长安地裂缝（fc1）金滹沱探槽东壁裂缝上盘，取样点距主裂缝水平距离6.7 m，取土深度5.5 m，其基本物理力学性质指标见表1。

表1 基本物理力学性质指标Table 1 Basic physical and mechanical properties

试验在CSS-2901TS 三轴流变试验机上进行，土样为直径为39.1 mm，高为80 mm 的圆柱形试样[19]。采用同一含水率（按天然含水率进行统一配置），固结压力σ3分别取100、200、300 kPa。试验控制条件为固结不排水，采用分级循环加、卸载方式，试验加载速率为0.001 kPa/s，卸载速率为0.005 kPa/s。按照常规三轴压缩试验获取的抗剪强度值，将应力分为5～8 级进行加载。对于每一级荷载设定相同的加、卸载稳定标准，即24 h 内加载蠕变量或卸载回弹蠕变量小于0.005 mm 或以恒定变形速率发展时即可认为稳定，然后卸载至围压状态，观测24 h 内无滞后恢复时，再施加下一级荷载，依此类推逐级进行。当蠕变曲线出现等速蠕变阶段后，势必会出现加速蠕变阶段，此时试样的应变速率急剧增大，试样在短时间内即达到破坏[20]。

3 试验结果及分析

3.1 蠕变曲线

按照“坐标平移法”对试验数据进行处理，得到了地裂缝带Q3原状黄土在100、200、300 kPa 围压下的蠕变加卸载曲线，如图1 所示。

图1 不同围压下试样的蠕变加、卸载试验曲线Fig.1 Creep loading and unloading curves of samples under different confining pressures

对比3 个围压下的蠕变曲线可知，同一围压下，应力越大，试样达到稳定的时间越长，反之越短；不同围压的相同应力下，试样的蠕变变形量基本一致，且到达稳定所需的时间也基本一致；围压越大，试样达到破坏时所需应力越大；蠕变曲线一旦出现等速蠕变阶段，则必将出现加速蠕变阶段，最终导致试样破坏。相应的试样破坏形态如图2 所示。

从图2 可以看出，100、200 kPa 围压下试样破坏时鼓胀型特征不明显，300 kPa 围压下试样破坏形态呈明显鼓胀型；随着围压的增大，试样的变形量逐渐增大。

3.2 应变速率与时间关系曲线

为了更好地分析蠕变特性，从相应的蠕变曲线中选择数条典型曲线进行分析，绘制相应的应变速率与时间关系曲线，如图3 所示。

图2 不同围压下试样的破坏形态Fig.2 Failure modes of samples under different confining pressures

图3 不同围压时低应力及高应力下应变速率与时间关系曲线Fig.3 Curves of strain rate vs.time under low and high stresses and different confining pressures

图3(a)、3(b)、3(c)分别为100、200、300 kPa围压下低应力及较高应力（左图）和高应力（右图）水平下的应变速率与时间关系曲线。从图可以看出，在低应力及较高应力水平下，应变速率随时间逐渐减小，最终趋于0，符合减速蠕变阶段特征，且随着应力水平的增大，相应的应变速率也越大；在高应力水平下，应变速率随时间先减小，后恒定，最后急剧增大，符合蠕变曲线经历减速蠕变、等速蠕变和加速蠕变3 个阶段的过程；加速蠕变段最终应变速率比初始应变速率大，且随着破坏应力的增大，相应的应变速率也越大，破坏所需时间越短。

对比3 个围压下的应变速率与时间关系曲线可知，无论围压大小，试样在破坏之前的各级应变速率均是由大到小变化，最终为0；一旦出现应变速率持续相等的情况，最终必将出现应变速率急剧变大直至试样破坏；试样最终破坏时的应变速率总是大于加载时的初始应变速率；随着围压的增大，试样出现加速蠕变即达到破坏所需应力越大，应变速率也越大。

4 蠕变本构模型的建立

4.1 模型辨识

力学模型理论是根据不同情况将材料抽象成弹簧、黏壶和滑块等元件组成的复杂体系，元件之间不同的组合代表材料的不同蠕变特性。基本力学模型是由这3 个元件的串并联组成的，共形成7 个模型[21]。将其中4 个与时间有关的模型即黏弹性、黏弹塑性、黏性和黏塑性称为基本流变力学模型[12]。为了研究与时间有关的变形形态，考虑材料一般均具有瞬时弹性变形，从而可以将弹簧与基本流变力学模型进行串联组合，共形成15 个流变力学模型。统一流变力学模型（如图4 所示）是将弹簧与4 个基本流变力学模型同时串联组成的模型，它是包含所有流变形态的最复杂最完整的一个模型[12-14]。

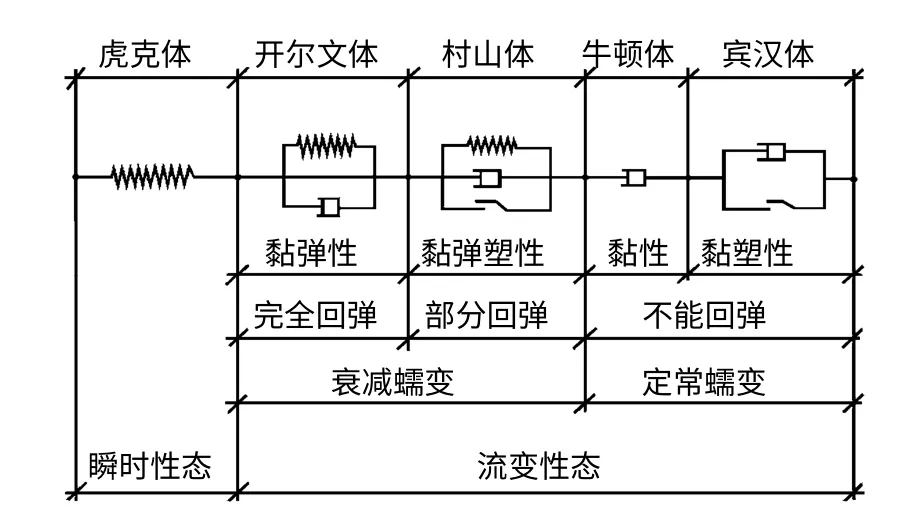
图4 统一流变力学模型[14]Fig.4 Unified rheological model[14]

基于统一流变力学模型理论，结合此次试验蠕变曲线对模型进行辨识：

（1）在加载瞬间均有瞬时变形产生，说明具有瞬时弹性变形性态，即本构模型中应串联有单独的弹簧元件。

（2）在很低应力下，蠕变曲线为减速蠕变类型，且能够完全回弹，说明具有黏弹性形态。

（3）在低应力及较高应力水平下，蠕变试验曲线均为减速蠕变，说明不具有完全黏性形态，即模型中没有单独的黏壶存在。

（4）在高应力水平下，蠕变试验曲线出现等速蠕变阶段，且最终出现加速蠕变阶段，说明低应力下该元件不起作用，当应力达到一定值时才起作用，为黏塑性体。

（5）分析较高应力下加卸载曲线，卸载后蠕变变形有且仅有部分回弹，则必有黏弹塑性体。

于是辨识出的本构模型与统一流变力学模型相比仅少了一个黏性体，是由西原体和村山体串联而成，命名为“改进西原模型”，如图5 所示。

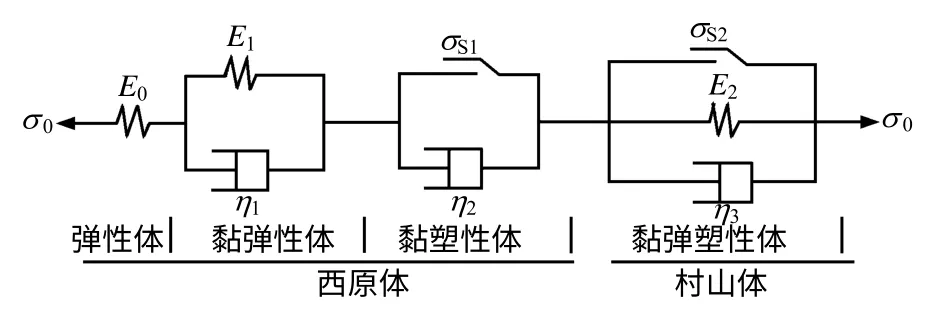
图5 改进西原模型（一维）Fig.5 Improved Nishihara model(one-dimensional)

根据模型的特点，屈服应力的大小不同，蠕变曲线表现出两种形式，如图6 所示。从图可以看出，在低应力水平下，无论屈服应力大小，蠕变曲线均仅有减速蠕变阶段，且卸载后变形完全回弹；在较高应力水平下，图6(a)的蠕变曲线具有减速蠕变和等速蠕变阶段，卸载后变形部分回弹；图6(b)的蠕变曲线仅具有减速蠕变阶段，卸载后变形部分回弹；在高应力水平下，无论屈服应力大小，蠕变曲线均具有减速蠕变和等速蠕变阶段。

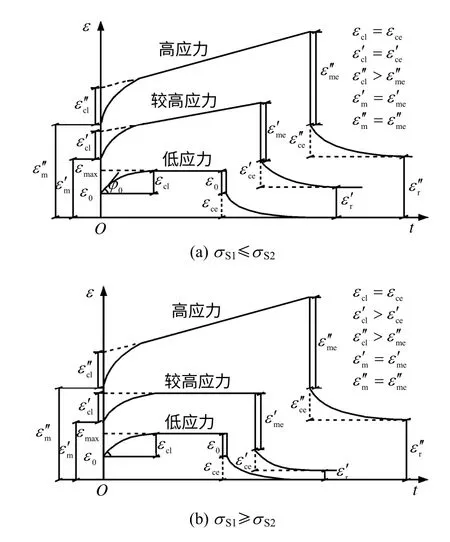
图6 改进西原模型蠕变曲线特征Fig.6 Creep characteristics of improved Nishihara model

从前述试验结果可以看出，蠕变曲线在低应力及较高应力水平下均表现为减速蠕变阶段，符合图6(b)情况，相应的一维本构方程为

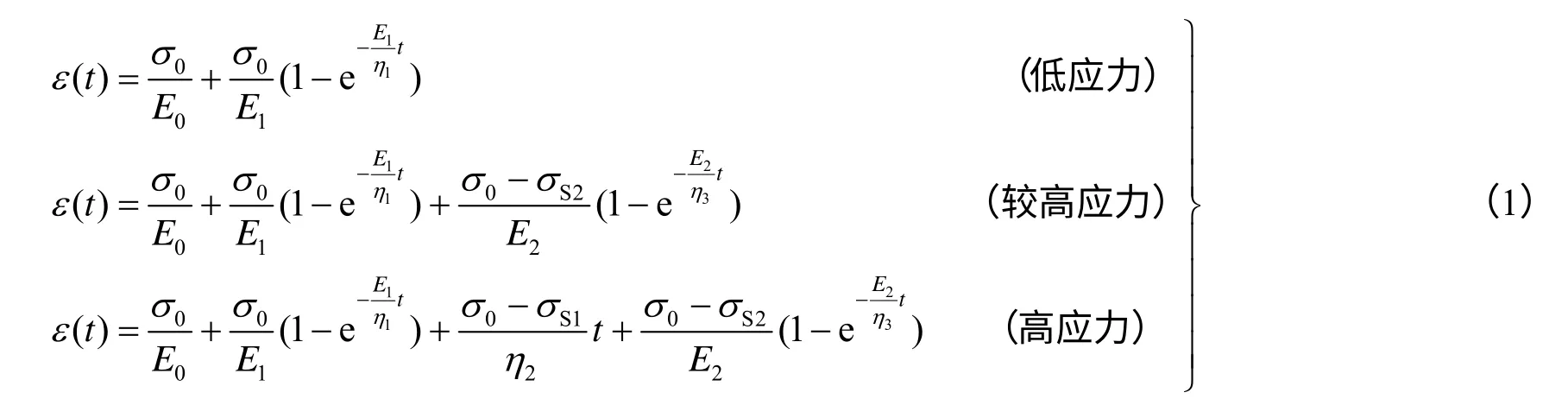
式中：ε(t)为蠕变量；t为施加应力的时间；σ0为施加的应力；E0、E1、E2分别为弹性体、黏弹性体及黏弹塑性体中弹簧的弹性模量；η0、η1、η2分别为黏弹性体、黏塑性体及黏弹塑性体中黏壶的黏滞系数；σS1、σS2分别为黏塑性体和黏弹塑性体的屈服应力。

考虑实际工程问题均为复杂的三维问题，进行蠕变试验研究及数值模拟时也是三维状态，因此，需要将一维本构方程推广为三维形式。

采用德鲁克-普拉格（D-P）（广义米塞斯）屈服准则，可以得到平面应变状态下的三维蠕变本构模型[22-23]，如图7 所示，相应的本构方程见式（2）。

图7 改进西元模型（三维）Fig.7 Improved Nishihara model(three-dimensional)

式中：σ1、σ2为施加的应力；K为弹性体积模量；G0为弹性剪切模量；G1、G2分别为黏弹性及黏弹塑性剪切模量；H1、H2、H3分别为黏弹性、黏塑性和黏弹塑性体积模量；F为屈服函数，F=，其中，I1、J2分别为第一应力不变量、第二应力偏量不变量，α为与黏聚力c 有关的系数，k为与内摩擦角φ 有关的系数，分别为

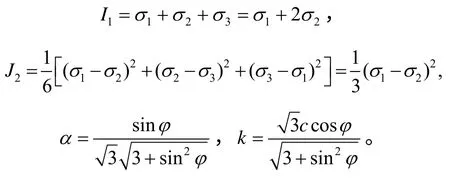
4.2 参数辨识

根据蠕变试验数据，分别对一维和三维本构方程各参数进行一一辨识。

4.2.1 一维本构方程参数辨识方法[13]

通过蠕变曲线上的瞬时变形 ε0，可以求得不同应力水平下对应的弹性模量 E0，即

通过低应力水平即σ0≤σS1、σS2时，蠕变曲线达到稳定时的最终蠕变量 εc(∞)确定黏弹性参数 E1和η1，即按式（1）中低应力对应的本构方程，当，可得

在蠕变曲线上任取一点(εc(t),t)，可得

通过高应力水平即σ0≥σS1、σS2时，蠕变曲线直线段斜率k1来确定黏塑性参数η2，即

通过较高应力水平即σS2≤σ0≤σS1时，对应的蠕变和回弹曲线及已辨识的 E1和η1求得黏弹塑性参数。按式（1）中较高应力对应的本构方程，可得：

在蠕变加载状态下，蠕变量 εc(t)与加载历时t的关系为

在蠕变卸载状态下，可恢复的蠕变量 εce(t)与卸载历时t 的关系为

式（7）减式（8），可得卸载状态下不可恢复的蠕变量 εcir(t)与卸载历时t 的关系为

当 t→∞时，

于是可得

将式（13）代入式（11），在蠕变曲线上任取一点(εcir(t),t)代入，得

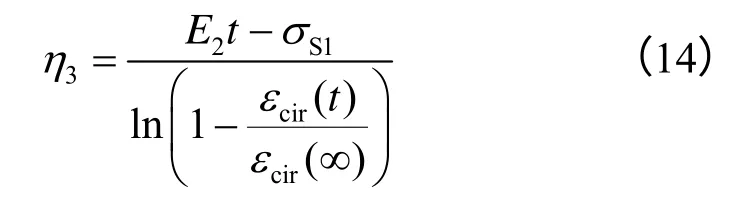
4.2.2 三维本构方程参数辨识方法[22-23]

根据弹性剪切模量 G0、弹性体积模量K、弹性模量E 及泊松比μ 之间的关系可得，

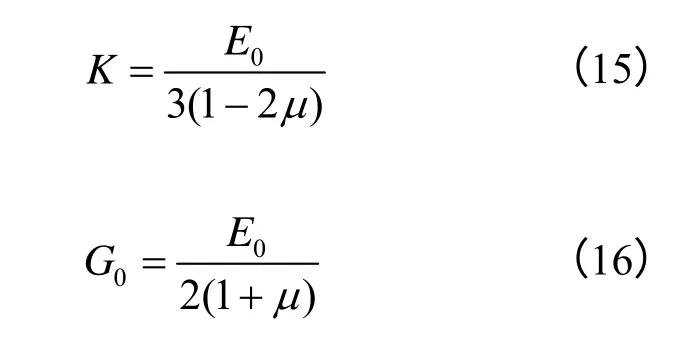
当 t=0时，式（2）中高应力对应的本构方程变为

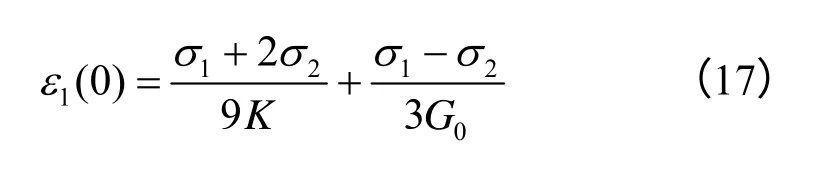
当 t→∞时，式（2）中高应力对应的本构方程变为

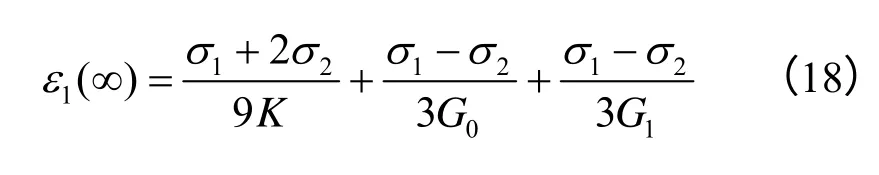
将式（17）、（18）代入式（2）中高应力对应的本构方程中，可得

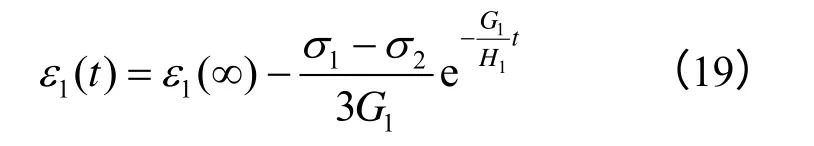
移项后得

对上式两边取对数：

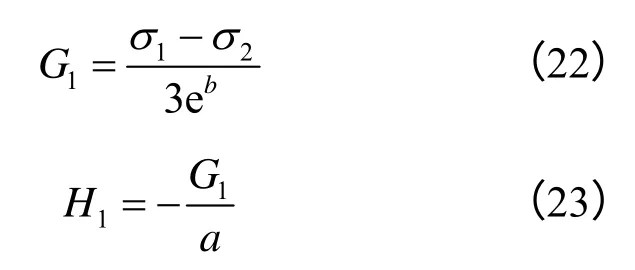
根据高应力下蠕变曲线直线段斜率k2，即式（2）中高应力对应的本构方程与时间呈线性关系的黏塑性体的系数确定H2：

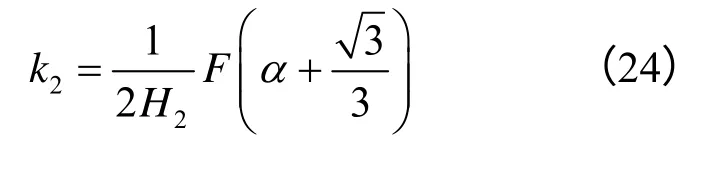
在蠕变加载状态下，蠕变量 εc(t)与加载历时t的关系为

在蠕变卸载状态下，可恢复的蠕变量 εce(t)与卸载历时t 的关系为

二者相减可得卸载状态下不可恢复的蠕变量εcir(t)与卸载历时t 的关系：

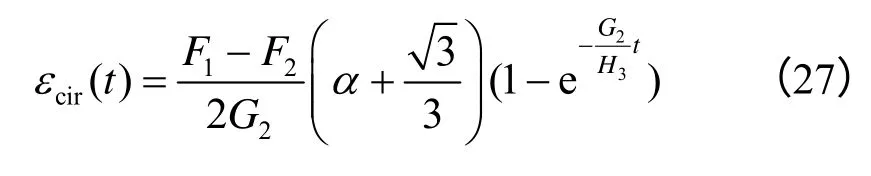
式中：F1、F2分别为加载时、卸载后的屈服函数。

当 t→∞时，式（25）、（27）分别化为

可得

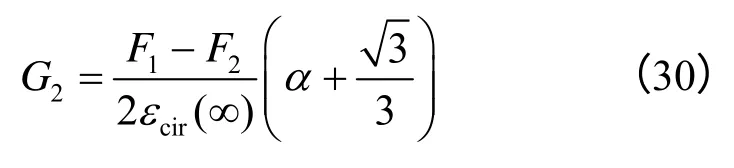
将式（29）代入式（27），在蠕变曲线上任取一点(εcir(t),t)，得

依据上述步骤，选取适合的蠕变试验曲线便可辨识出三维本构方程的所有参数，见表2。

从表2 可以看出，随着围压增大，试样达到破坏所需的应力越大；随着应力增大，除黏弹性参数不变外，其他参数均呈现先增大后减小的现象；相同应力条件下，围压越大，相应的参数越小。

为验证参数的合理性，将由上述参数所得本构方程绘制的曲线与相对应的试验数据点进行对比分析，如图8 所示。

从图中可以看出，模型曲线与试验数据点拟合的较好，说明通过辨识后选取的模型和确定的模型参数都较好。限于篇幅，在此仅给出了模型参数的辨识方法。

图8 不同围压下模型曲线与试验数据点对比图Fig.8 Comparison between simulated curves and experimental data points under different confining pressures

5 结 论

（1）在天然含水率状态下，西安地区地裂缝带Q3原状黄土的蠕变曲线表现为：加载瞬间均有瞬时变形产生，在低应力水平下，蠕变曲线表现为减速蠕变阶段，卸载时变形完全回弹。

（2）在较高应力水平下，蠕变曲线表现为减速蠕变阶段，卸载时变形部分回弹。

（3）在高应力水平下，蠕变曲线表现为等速蠕变阶段，且最终出现加速蠕变阶段直至试样破坏。

（4）通过模型曲线与试验数据点的对比可知，所得本构模型、参数均合理，能够较好地描述西安地区地裂缝带Q3原状黄土的流变特性。

[1]李永善.西安地裂缝[M].北京:地震出版社,1986.

[2]张家明.西安地裂缝研究[M].西安:西北大学出版社,1990.

[3]李永善,等.西安地裂缝及渭河盆地活动断层研究[M].北京:地震出版社,1992.

[4]LEONARD R J.An earth fissure in southern Arizona[J].Journal of Geology,1929,37(8):765－774.

[5]LOFGREN B E.Hydraulic stresses cause ground movement and fissures,Picacho,Arizona[J].Geological Society American Abstracts Programs,1978,10(3):113.

[6]LOFGREN B E.Earth cracks caused by horizontal stresses[J].Earth Observation System,1984,65:882－883.

[7]HOLZER T L,GABRYSCH R K.Effect of water-level recoveries on fault creep,Houston,Texas[J].Ground Water,1987,25(4):392－397.

[8]易学发.西安市地面沉降及地裂缝成因的讨论[J].地震,1984,12(6):50－54.YI Xue-fa.A discussion on the ground subsidence and the genesis of ground fissure in Xi’an city[J].Earthquake,1984,12(6):50－54.

[9]刘国昌.西安的地裂缝[J].西安地质学院学报,1986,8(4):9－22.LIU Guo-chang.The ground fissures in Xi’an,Shaanxi[J].Journal of Xi 'an Institute of Geology,1986,8(4):9－22.

[10]彭建兵,等.渭河盆地活动断裂与地质灾害[M].西安:西北大学出版社,1992.

[11]SCOTT R F.土力学原理[M].张孟喜译.武汉:华中科技大学出版社,2007.

[12]夏才初,王晓东,许崇帮,等.用统一流变力学模型理论辨识流变模型的方法和实例[J].岩石力学与工程学报,2008,27(8):1594－1600.XIA Cai-chu,WANG Xiao-dong,XU Chong-bang,et al.Method to identify rheological models by unified rheological model theory and case study[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(8):1594－1600.

[13]夏才初,许崇帮,王晓东,等.统一流变力学模型参数的确定方法[J].岩石力学与工程学报,2009,28(2):425－432.XIA Cai-chu,XU Chong-bang,WANG Xiao-dong,et al.Method for parameters determination with unified rheological mechanical model[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(2):425－432.

[14]夏才初,孙钧.统一流变力学模型的若干问题研究[C]//第六次全国岩石力学与工程学术大会论文集.武汉:中国学术期刊电子出版社,2000.

[15]王艳婷.黄土流变特性试验分析及本构模型的研究[D].西安:长安大学,2006.

[16]李良权,徐卫亚,王伟.基于西原模型的非线性黏弹塑性流变模型[J].力学学报,2009,41(5):671－680.LI Liang-quan,XU Wei-ya,WANG Wei.A nonlinear viscoelastoplastic rheological model based on Nishihara’s model[J].Chinese Journal of Theoretical and Applied Mechanics,2009,41(5):671－680.

[17]彭建兵,陈立伟,黄强兵,等.地裂缝破裂扩展的大型物理模拟试验研究[J].地球物理学报,2008,51(6):1826－1834.PENG Jian-bing,CHEN Li-wei,HUANG Qiang-bing,et al.Large-scale physical simulative experiment on ground fissure expansion mechanism[J].Chinese Journal of Geophysics,2008,51(6):1826－1834.

[18]徐继山,彭建兵,马学军,等.邢台市隆尧地裂缝发育特征及成因分析[J].工程地质学报,2012,20(2):160－169.XU Ji-shan,PENG Jian-bing,MA Xue-jun,et al.Characteristic and mechanism analysis of ground fissuresin Longyao,Xingtai[J].Journal of Engineering Geology,2012,20(2):160－169.

[19]南京水利科学研究院.SL237-1999 土工试验规程[S].北京:中国水利水电出版社,1999.

[20]袁聚云,徐超,赵春风,等.土工试验与原位测试[M].上海:同济大学出版社,2004.

[21]周德培.流变力学原理及其在岩土工程中的应用[M].成都:西南交通大学出版社,1995.

[22]王芝银,李云鹏.岩体流变理论及其数值模拟[M].科学出版社,2008.

[23]孙钧.岩土材料流变及其工程应用[M].中国建筑工业出版社,1999.