湘南地区红黏土动态回弹模量试验与预估模型研究
2015-02-04李志勇邹静蓉邹维列
李志勇,董 城,邹静蓉,邹维列
(1.湖南省交通科学研究院,湖南 长沙 410015;2.中南林业科技大学 土木工程与力学学院,湖南 长沙 410004;3.武汉大学 土木建筑工程学院,湖北 武汉 430072)
1 引 言
湘南地区由于特殊的气候及地质条件,广泛分布着高液限红黏土,它具有高的天然含水率、大的孔隙比和较强的结构性等特点。用红黏土作为路堤填料主要存在三大问题,即天然含水率高、水稳定性较差和压实困难。在当前节能环保要求不断提高和用地日趋紧张的情况下,充分利用当地红黏土填筑路基是发展的方向与必然趋势。随着我国经济的发展,高速和重载是未来交通线路必然的趋势。潮湿多雨的气候特点与重载交通的不利组合,使得湘南红黏土路基的稳定问题尤为突出。目前,关于红黏土的填筑控制国内已有一些报道[1-2],但很少涉及红黏土路基在交通荷载作用下的稳定性研究。
路基土动态回弹模量(简称回弹模量)作为柔性路面力学-经验设计方法中表征路基土力学特性的主要参数之一[3],能很好地反映路基土的稳定性能。研究表明,路基土回弹模量的主要影响因素有土的类型[4]、应力状态[5]、含水率[6]、加载序列[7]、基质吸力[8]和压实度[9]等。当土的类型和压实度确定后,回弹模量主要受含水率和应力状态的影响。
路基土动态回弹模量的测量主要分为室内和室外两种方式。室外现场测试主要是基于无损检测技术,通过模量反算法来获得回弹模量[10]。室内测试通过现场取样、室内制样,进行重复加载动三轴试验来测定回弹模量[9],可全面研究各种影响因素,已成为目前主流的回弹模量测试方法。基于国外已有路基土回弹模量的影响因素研究成果[11],并结合我国典型路面结构应力水平、路基土类型,国内学者构建了基于室内重复加载三轴试验确定不同路基土回弹模量的标准方法[12]。
对于路基土动态回弹模量试验结果,通过选取应力、土的物理性质参数和环境状态为变量,运用多元回归的方法,可建立相应的回弹模量预估模型。最早的回弹模量预测模型由Seed 等[13]在研究路基土回弹特性与沥青路面疲劳损坏关系过程中提出,该模型认为回弹模量与体应力相关。许多学者在此工作基础上提出了拓展的回弹模量模型。根据所选应力变量的不同,它们大致可分为3 类:考虑体应力影响的单因素模型[13]、考虑剪应力和围压影响的复合模型[14]、考虑剪应力和体应力的复合模型[15]。为探讨各预估模型对于湘南地区红黏土的适用性,需要利用典型的回弹模量预估模型对试验数据进行拟合,遴选出最佳的模型。
本文以湘南地区红黏土为研究对象,通过室内动三轴试验测定不同应力状态、含水率和压实度下红黏土的回弹模量,分析影响红黏土动态回弹模量的因素及其规律。通过考虑偏应力、围压和体应力组合的复合回弹模量预估模型对试验数据进行评估,进而遴选出最佳的预估模型。
2 试验结果及分析
2.1 试验概况
2.1.1 试样制备
试验用红黏土试样基本物理性质列于表1,试验方法和条件沿用国内已有成果[5]。为分析应力状况、含水率、压实度和材料性质等上述因素对湘南地区红黏土回弹模量的影响规律,分别制作不同含水率ω(ωop-2%、ωop、ωop+2%、ωop+4%)和不同压实度P(90%、94%、96%)的试样,每组3 个平行试样。试验过程中,试样实际含水率与目标含水率误差不超过1%,压实度与目标压实度误差不超过2%。每个试样高度和含水率与平行试样均值误差不超过1%。

表1 土样基本物理性质Table 1 Physical properties of soil
2.1.2 试验过程
试验采用美国GCTS 公司动三轴测试系统,加载波形为半正弦波,荷载频率为1 Hz。路基土应力加载序列采用国内已有研究成果[12],路基土动态回弹模量测试中,某一加载级位下荷载循环次数为100 次,记录各级重复荷载作用下最后5 次循环的回弹变形平均值,按下式计算试件的动态回弹模量。

式中:MR为动态回弹模量;σd为偏应力;εR为轴向回弹应变均值。
2.2 应力状态与回弹模量关系
图1、2为红黏土在最佳含水率和96%压实度下动态回弹模量随偏应力和围压的关系曲线。当围压保持一定值时,动态回弹模量随偏应力的增加而减小:当偏应力一定时,动态回弹模量随围压的增加而增大,即湘南地区红黏土的动态回弹模量具有较强的应力依赖性。由于三轴试验中σ2=σ3=围压,体应力θ=σ1+σ2+σ3=3 σ3+σd,八面体剪应力τoct=,因此,方差分析时可仅讨论偏应力和围压。对红黏土在最佳含水率和96%压实度下动态回弹模量进行双因素方差分析,分析结果见表2。

表2 回弹模量双因素方差分析Table 2 Dual-factor analysis of variance for resilient modulus
由表2 可知,偏应力与围压对红黏土的动态回弹模量均有显著性影响,但相比较而言,红黏土动态回弹模量受偏应力的影响更为显著。

图1 动态回弹模量与偏应力关系Fig.1 Relation between dynamic resilient modulus and deviatoric stress

图2 动态回弹模量与围压应力关系Fig.2 Relation between dynamic resilient modulus and confining stress
2.3 含水率与压实度对回弹模量影响
为研究红黏土含水率和压实度对回弹模量的影响,分别进行了4 种含水率和3 个压实度的动三轴试验,结果如图3 所示。由图可知,回弹模量受含水率的影响较大。在ωop干侧,动态回弹模量随含水率的增大而增大;在 ωop湿侧,动态回弹模量随着含水率的增大而降低,但在ωop湿侧随含水率的变化较干侧更明显;同时,回弹模量最大值出现在最佳含水率附近。例如,当压实度为96%、围压为60 kPa、偏应力为35 kPa 时,相对于含水率 ωop,含水率为 ωop-2%、ωop+2%和opω+4%时的回弹模量分别减少了31.23%、34.82%和40.45%。鉴于红黏土的天然含水率一般大于最佳含水率,为防止含水率增加导致的路基土动态回弹模量的过大衰弱,一般要求碾压含水率控制在ωop~ωop+4%范围内。

图3 含水率和压实度对动态回弹模量的影响Fig.3 Effect of water content and compaction degree on dynamic resilient modulus
从图3 还可看出,在相同含水率下,红黏土动态回弹模量随着压实度的提高而增大。不同含水率下提高压实度能有效的提高路基土动态回弹模量。如围压为60 kPa、偏应力为35 kPa 时,在最佳含水率下,相对于90%压实度、压实度为94%和96%时的动态回弹模量分别提高了3.92%和52.79%。同时,压实度对回弹模量的影响随着含水率的增加而减弱。因此,对于红黏土路基而言,在保证路基强度要求前提下,压实度一般要求控制在90%以上。
3 回弹模量预估与分析
3.1 回弹模量预估模型
已有研究表明,路基土动态回弹模量主要受其应力状况、含水率、压实度和材料性质等因素的影响[16-17]。回弹模量预估模型主要回弹模量的应力相关性,考虑偏应力、体应力和围压对它的影响。对于湘南地区红黏土动态回弹模量的预估,采用如下3 个典型复合模型。
3.1.1 UZAN 模型
UZAN 在回弹模型中引入偏应力和体应力项,以表征剪应力和体应力的共同影响[11],见下式:

式中:k1、k2和k3为材料参数,通过对试验数据进行回归得到。
由于模型中既包含了体应力θ 项,又包含了偏应力 σd项,所以式(2)对应力软化和应力强化材料都适用。该模型的缺点在于:①存在量纲问题;②存在模量不定值问题:当σd=0时,MR→∞;当 σ1=σ3=0,MR=0·∞。
3.1.2 NI 模型
NI 等[14]通过试验发现,回弹模量对围压非常敏感,通过引入围压和偏应力对UZAN 模型进行如下修正:

式中:pa为参照大气压(这里取 pa=100 kPa)。
通过对式(2)的改进,式(3)消除了量纲和模量不定值问题。
3.1.3 N37A 模型
美国国家公路联合研究计划(NCHRP)开展了新的路面设计方法研究,并在2004年NCHRP 1-37A项目中提出公路路基设计的动态回弹模量模型[18],(文后简称N37A 模型)。其方程如下:

式中:τoct为八面体剪应力。
该模型综合考虑了体应力和剪应力对回弹模量的影响,同时克服了量纲不统一、模量不定值等问题,因而具有较广泛的适用性。对比式(2)、(4)发现,N37A 模型将偏应力替换成八面体剪应力,这在本质上与UZAN 模型是一致的(动三轴情况下,八面体剪应力和体应力成比例关系)。同时,N37A 模型在在八面体剪应力后加了常数1,不仅克服了模量不定值问题,还削弱了偏应力变化对回弹模量的影响。
3.2 不同回弹模量预估模型预测结果
对各种工况下试验数据进行回归分析,分别得到了不同回弹模量预估模型粉土在不同含水率、压实度的情况下的预估参数和决定系数,模拟结果见图4、5和表3。从表3 的回归结果可以看出,对于湘南地区的红黏土,NI 模型对试验数据拟合程度最好,N37A 模型次之,UZAN 模型最差。
表4和图6 给出了最佳含水率、压实度为96%的红黏土回弹模量实测数据和3 种模型预估数据及相对误差,可以发现 NI 模型的最大误差值为7.461%,N37A 模型误差值最大为8.425%,UZAN模型误差值最大为8.008%。对于N37A、NI和UZAN模型的平均误差和方差分别为 3.33%±2.85%,3.15%±2.55%和3.18%±2.69%。由此可知,NI 模型的平均误差和方差均最小。
需要指出,上述评估结果仅适用于文中试验条件下的湘南地区红黏土的回弹模量预测。

图4 不同回弹模量模型的预测值和试验值Fig.4 Predicted and experimental resilient moduli with different prediction models
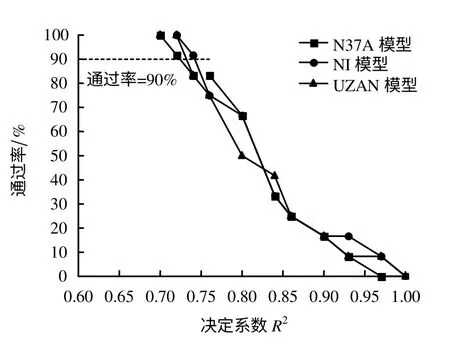
图5 不同回弹模量预估模型决定系数Fig.5 Determination coefficients of different prediction models for resilient modulus

表3 不同回弹模量预估模型参数Table 3 Parameters of different prediction models for resilient modulus

表4 不同回弹模量预测结果和试验结果Table 4 Predicted and experimental resilient moduli with different prediction models

图6 不同回弹模量模型预测误差Fig.6 Prediction errors of different prediction models for resilient modulus
3.3 回弹模量预估模型参数分析
通过第3.2 节的分析可知,NI 模型对红黏土的回弹模量拟合最佳。本节对NI 模型的材料参数k1、k2、k3分布进行分析,结果如图7 所示。对于红黏土,k1为表征路基土刚度的参数,与路基土动态回弹模量成正比,其值随有效应力的增加而增大,总体上其在最优含水率附近达到最大值,而在最优含水率干侧和湿侧其值降低,同时随着压实度提高而增大。k2反映了路基土动态回弹模量随体应力的增加而硬化的特性,总体上随着含水率的增加而减小,随压实度的增加而增大。k3表现为负值,表征了路基土动态回弹模量随着剪应力的增加而软化的特性,其值随着含水率和压实度的变化不明显。

图7 参数k1、k2、k3的分布Fig.7 Distributions of parameters k1,k2,k3
4 结 论
(1)在围压一定时,红黏土回弹模量随偏应力的增大而减小,随体应力的增加而增大;在偏应力一定时,随围压的增加而增大;偏应力和围压对红黏土回弹模量均有显著性影响,但偏应力的影响更为显著。
(2)红黏土回弹模量受含水率影响较大,整体上随含水率的增加先增大后变小,并在最佳含水率附近达最大值;在相同含水率下,回弹模量随着压实度的提高而增大,并且在最佳含水率时提高最大。为防止含水率增加和压实度降低导致路基土回弹模量过大衰减,在保证路基强度要求的前提下,对于红黏土路基而言,一般要求碾压含水率控制在ωop~ ωop+4%范围内,压实度控制在90%以上。
(3)采用3 种应力相关的典型动态回弹模量预估模型对试验数据进行回归分析,误差分析表明,对于湘南地区红黏土,NI 模型具有更高的决定系数,能更好地拟合红黏土动态回弹模量;同时,给出了NI 材料参数的分布图。
上述试验和理论研究结果为湘南地区评价红黏土路基在环境和交通荷载作用下的稳定性分析提供了依据。
[1]万智,郭爱国,谈云志,等.湘西南红黏土路堤填筑技术研究[J].岩土力学,2011,32(8):2281-2286.WAN Zhi,GUO Ai-guo,TAN Yun-zhi,et al.study of embankment filled technology of laterite soil in Southwest Hunan[J].Rock and Soil Mechanics,2011,32(8):2281-2286.
[2]谈云志,孔令伟,郭爱国,等.红黏土路基填筑压实度控制指标探讨[J].岩土力学,2010,31(3):851-855.TAN Yun-zhi,KONG Ling-wei,GUO Ai-guo,et al.Discussion on the compaction degree index of subgrade filled with laterite[J].Rock and Soil Mechanics,2010,31(3):851-855.
[3]黄仰贤.路面分析与设计[M].北京:人民交通出版社,1998:215-220.
[4]凌建明,苏华才,谢华昌,等.路基土动态回弹模量的试验研究[J].地下空间与工程学报,2010,6(5):919-925.LING Jian-ming,SU Hua-cai,XIE Hua-chang,et al.Library research on dynamic resilient modulus of subgrade soil[J].Chinese Journal of Underground Space and Engineering,2010,6(5):919-925.
[5]董城,冷伍明,李志勇.粉土动态回弹模量试验研究[J].中南大学学报(自然科学版),2012,43(12):4834-4839.DONG Cheng,LENG Wu-ming,LI Zhi-yong.Dynamic resilient modulus of silt[J].Journal of Central South University(Science and Technology),2012,43(12):4834-4839.
[6]凌建明,陈声凯,曹长伟.路基土回弹模量影响因素分析[J].建筑材料学报,2007,10(4):446-451.LING Jian-ming,CHEN Sheng-kai,CAO Chang-wei.Analysis of influence factors on resilient modulus of subgrade soils[J].Journal of Building Materials,2007,10(4):446-451.
[7]MUHANNA A S,RAHMAN M S,LAMBE P C.Resilient modulus measurement of fine-grained subgrade soils[R].Washington D C:National Research Council,1999.
[8]杨树荣,拱祥生,黄伟庆,等.非饱和黏性路基土回弹模量之研究[J].岩土工程学报,2006,28(2):225-229.YANG Shu-rong,KUNG Johnson H S,HUANG Wei-hsing,et al.Resilient modulus of unsaturated cohesive subgrade soils[J].Chinese Journal of Geotechnical Engineering,2006,28(2):225-229.
[9]LEKARP F,ISACSSON U,DAWSON A.State of the art I:Resilient response of unbound aggregates[J].Journal of Transportation Engineering,2000,126(1):66-75.
[10]查旭东.基于同伦方法的路面模量反算的研究[D].西安:长安大学,2001.
[11]罗志刚.路基与粒料层动态模量参数研究[D].上海:同济大学,2007.
[12]陈声凯,凌建明,张世洲.路基土动态回弹模量室内试验加载序列的确定[J].公路,2006,11(5):148-152.CHEN Sheng-kai,LING Jian-ming,ZHANG Shi-zhou.Fixing loading sequence for resilient modulus test of subgrade soil[J].Highway,2006,11(5):148-152.
[13]SEED H B,CHAN C K,MONISMITH C L.Effects of repeated loading on the strength and deformation of compacted clay[J].HRB Proceedings,1955,34:541-558.
[14]NI B,HOPKINS T C,SUN L,et al.Modeling the resilient modulus of soils[C]//Proceedings of the 6th International Conference on the Bearing Capacity of Roads,Railways and Airfields.Lisbon:A.A.Balkema,2002:1131-1142.
[15]UZAN J.Characterization of granular materials[R].Washington D C:National Research Council,1985.
[16]张世洲,凌建明,罗志刚,等.路基土动态模量试验研究[J].北方交通,2008,6(4):18-21.ZHANG Shi-zhou,LING Jian-ming,LUO Zhi-gang,et al.Research on experiment of dynamic modulus of subgrade soil[J].Northern Communications,2008,6(4):18-21.
[17]董城,冷伍明,李志勇,等.水泥改良高液限黏土动态回弹模量试验研究[J].岩土力学,2013,34(1):133-138.DONG Cheng,LENG Wu-ming,LI Zhi-yong,et al.Experimental study of dynamic resilient modulus of cement-improved high liquid limit clay[J].Rock and Soil Mechanics,2013,34(1):133-138.
[18]陈声凯,凌建明 罗志刚.路基土回弹模量应力依赖性分析及预估模型[J].土木工程学报,2007,40(6):95-99.CHEN Sheng-kai,LING Jian-ming,LUO Zhi-gang.Stress-dependent characteristics and prediction model of the resilient modulus of subgrade soils[J].China Civil Engineering Journal,2007,40(6):95-99.
