考虑围岩蠕变全过程与扩容的深埋隧洞非线性位移解
2015-02-04蔡燕燕张建智陈士海
蔡燕燕 ,张建智,俞 缙 ,陈士海
(1.华侨大学 岩土工程研究所,福建 厦门 361021;2.中国矿业大学 深部岩土力学与地下工程国家重点实验室,江苏 徐州 221008)
1 引 言
陈宗基院士在1959年首次对一个完整隧洞进行蠕变试验,指出必须把坚牢的岩石视为弹黏塑性材料,它能通过向内运动把内应变能释放一部分[1]。之后,人们开始将时效变形概念引入隧洞围岩应力、应变分析中[2]。目前,隧洞正在向“长大深”方向发展,深埋隧洞工程遇到的蠕变问题更为突出,越来越受到学者的重视。深埋隧洞开挖支护后,在高地应力下中等强度围岩蠕变表现为非线性[3],一段时间后,可能发生累积大变形而导致隧洞支护结构破坏。深入研究深埋隧洞围岩非线性蠕变问题和解析方法,具有重要的理论价值和实践意义。
当深埋隧洞围岩长期强度低于高地应力时,岩体会出现蠕变全过程中的加速阶段,这与一般隧洞围岩多处于蠕变衰减和稳定阶段有显著差异。另一方面,研究表明,岩体塑性体积变化(多表现为扩容)会影响围岩应力分布,进而改变围岩位移场,在分析时特别需要重视。若忽略其影响,则会低估围岩径向应变和塑性区半径。因此,深埋隧洞应力和位移解析分析需同时考虑围岩塑性体积变化及加速蠕变的影响,然而现有的研究还很不成熟。于学馥[4]、Nomikos[5]和Sulem[6]等推导的黏弹性解或黏弹塑性解,没能考虑围岩蠕变加速阶段和塑性体积变化的影响。Fahimifar 等[7]推导静水压力圆形隧洞变形解并预测了蠕变位移。卢爱红等[8]探讨隧洞位移、支护反力与黏性系数与时间的关系,二者均忽略了塑性体积变化的影响。Fritz[9]考虑应变软化因素推导围岩黏弹塑性解。卞跃威等[10]考虑塑性软化、塑性体胀和应力释放,推导圆形隧洞黏弹塑性解并对围岩衰减蠕变特性做了探讨。余东明等[11]假设围岩为Burgers 体与Drucker-Prager 准则组合的黏弹塑性材料,获得剪胀影响下的隧洞黏弹塑性蠕变位移解析式,但他们均未考虑围岩蠕变全过程的3个阶段,尤其忽略了蠕变加速阶段。最近,国外学者注意到该问题,试图建立考虑围岩加速蠕变和扩容影响的分析方法。Sterpi 等[12]采用考虑弹塑性、黏弹性和的黏塑性蠕变模型,研究高地应力下隧洞围岩的3 阶段蠕变行为,可惜未得出解析解。
由研究现状可知,深埋隧洞围岩蠕变是一个多因素影响的非线性力学问题,围岩蠕变模型的合理使用是解析求解的关键。常用的围岩蠕变力学模型,如西原模型、Burgers 体组合模型、宾汉姆模型等,均不能反映围岩加速蠕变特性。为获得围岩蠕变3阶段的深埋隧洞位移解,文中基于一定假设,尝试采用河海模型进行理论求解。河海模型是由西原模型发展得到的黏弹塑性模型(后者为前者在流变指数为1 时的特例),可充分反映岩石的加速蠕变特性。在解析中同时考虑岩石塑性扩容特性,推得了考虑与不考虑洞周面力的初始弹塑性应力解及围岩黏弹塑性区非线性蠕变位移表达式。针对蠕变参数(NVPB 黏滞系数η3和蠕变指数n)以及在不同m值情况下,讨论了洞周面力与扩容角对隧洞洞壁蠕变位移的影响规律。研究结论对隧洞围岩的临崩预报有一定指导意义。
2 基本假设与围岩蠕变模型
2.1 基本假设
(1)如图1 所示,深隧半径为R0,且纵向无限长,原岩应力p0表现为静水状态,洞周面力为pi,含隧洞内径处围岩自身及掌子面提供的假想支护力pc和支护结构提供的抗力ps。
(2)隧洞开挖产生的应力重分布完成后,围岩应力场恒定,在此应力场作用下围岩发生蠕变。蠕变现象符合空间轴对称假设。
(3)隧洞围岩进入屈服前为黏弹性不可压缩体,服从Hooke 定律,同时考虑蠕变现象。进入屈服后为黏弹塑性可压缩体,蠕变应变含弹性应变、黏弹性应变和黏塑性应变。
(4)围岩弹、塑性区长期强度相同,塑性区围岩变形模量随着塑性应变的增加而逐渐降低,假设蠕变参数G、η 线性弱化。
(5)围岩应力以受压为正,相应的应变亦为正,以向隧洞中心发展的位移为正。

图1 隧洞力学模型Fig.1 Mechanical model of tunnel
2.2 围岩蠕变模型
当深埋隧洞围岩长期强度低于高地应力时,须考虑蠕变的全过程,蠕变模型必须充分反映围岩的衰减、稳定和加速蠕变。徐卫亚等[13]采用非线性蠕变元件代替法建立了河海模型,可完整地描述岩石蠕变的3 个阶段。河海模型是指在五元件线性黏弹性蠕变模型上串联一个非线性黏塑性体(nonlinear viscous-plastic body,NVPB)而组成的模型,文献[13]通过岩石全自动流变伺服仪进行三轴蠕变试验、FLAC3D数值程序模拟以及锦屏一级水电站工程验证,说明该模型可充分反映岩石的加速蠕变特性,模型如图2 所示。图中,河海模型由Hooke 体、2 个线性黏弹性体(广义Kelvin 体)、非线性黏塑性体(NVPB)串联而成。其中,σ为一维应力(MPa),E0为Hooke 体弹性模量,E1和E2、η1和η2均为广义Kelvin 体弹性模量和黏滞系数,η3为NVPB 黏滞系数,n为蠕变指数,σs为长期强度。当σ ≤σs时,NVPB 部分表现为刚体,不参与蠕变,模型将退化为理想黏弹性蠕变模型,适于描述岩石蠕变衰减及稳定阶段。当σ>σs时,河海模型适于描述岩石蠕变全过程行为。

图2 一维岩石非线性蠕变模型Fig.2 One-dimensional nonlinear creep model of rock
利用Laplace 变换及其逆变换可得蠕变应变表达式,见式(1)。由式(1)可知,当n≤1 时,dε/dt>0,d2ε/dt2<0,模型无法反映蠕变加速阶段。当n>1时,dε/dt>0,且存在 d2ε/dt2<0、d2ε/dt2=0 或d2ε/dt2>0 这3 种情况,分别对应岩石蠕变3 阶段行为,详见图3。


图3 岩石蠕变特征曲线Fig.3 Creep characteristic curve of rock
深埋隧洞围岩变形是复杂的三维问题,文献[13]给出了三维应力状态下岩石蠕变方程,见式(2)。经文献[14]修正,在三维本构关系中,黏弹性模量Ei(E0、E1和E2)应替换成黏弹性剪切模量Gi(G0、G1和G2),式(3)给出了两种模量关系式。
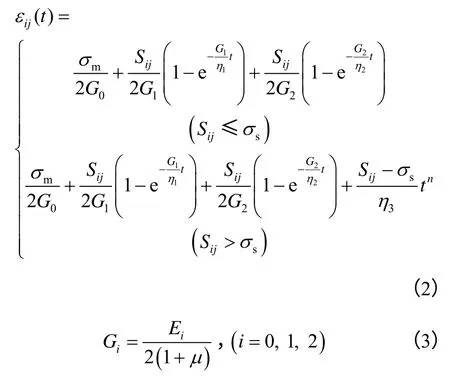
式中:t为时间;μ为泊松比;σm为平均应力;Sij为偏应力;则
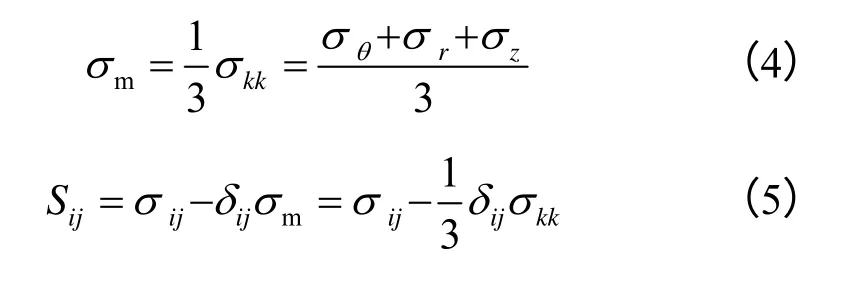
式中:σkk为应力张量第一不变量;σθ、σz和σr分别为围岩环向应力、轴向应力与径向应力;δij为Kronecker 符号。
3 隧洞围岩蠕变初始应力场
深埋隧洞开挖支护符合平面应变假设。由2.1节中基本假设(2)可知,围岩应力场形成以后保持恒定,并作为围岩蠕变前的初始应力场。因此,必须先求得该应力场,本文采用Hoek-Brown 屈服准则求解。Hoek-Brown 屈服准则作为非线性破坏准则,相比于线性Mohr-Coulomb 屈服准则更能反映深隧围岩的固有特点和非线性破坏特征,以及结构面组数、岩石强度、所处应力状态对围岩强度的影响。其常用公式为
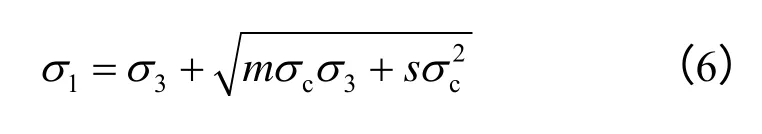
式中:σ1和σ3分别为岩体屈服时的最大主应力和最小主应力(MPa);σc为完整岩石的单轴抗压强度(MPa);m、s 均为与岩体特性有关的材料参数,量纲为1,m 反映岩体的软硬程度,取值为10-7~25,s 反映岩体破碎程度,取值为0~1。Hoek-Brown公式中岩体力学参数可通过文献[15]确定。令σ1= σθ,σ3= σr。
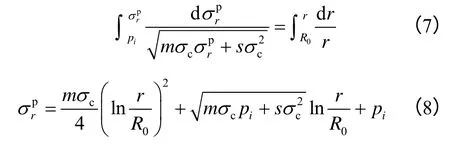
进而可得环向应力为
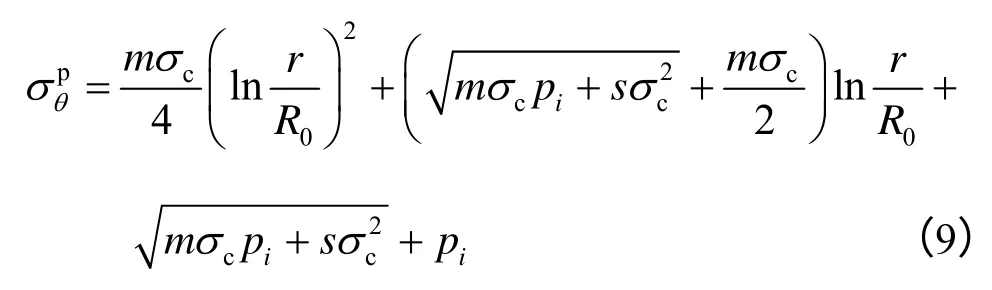
考虑到塑性体积变化的影响,采用文献[16]基于塑性势函数推得的平面应变条件下塑性中主应力计算式如下:
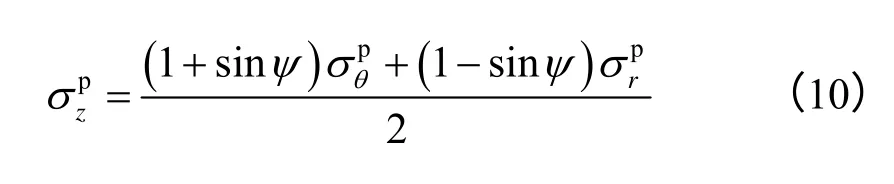
式中:ψ为岩体材料扩容角;则

在围岩弹性区,当r=Rp时,;且当r→∞时,σθ= σr=p0;故由平面应变理论可得弹性解:

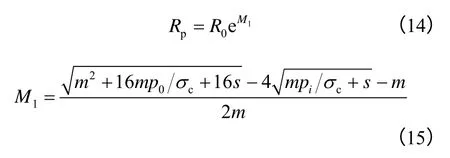
将式(14)代入式(12)、(13),可得弹性区应力场为
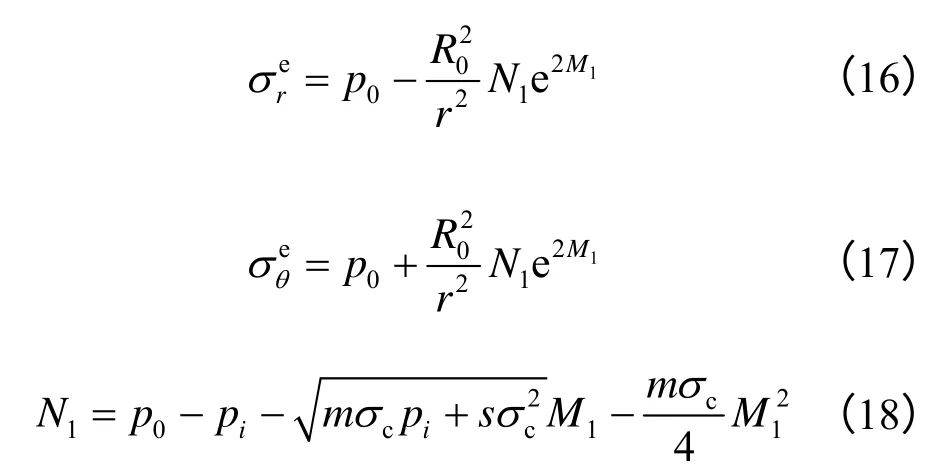
在弹性区,弹性中主应力表达式[17]为

特别注意,考虑隧洞内边界条件时,使用如下关系式:

孙钧[3]指出,空间约束效应使毗邻开挖面的围岩存在等效的假想支护力pc。该支护力随着开挖面的推进而逐渐减小(应力释放所致),随之支护结构发挥作用,其支护抗力ps从0 开始逐渐增加。当空间约束效应基本消失时,pc=0,ps=ps,max。卞跃威等[10]指出,在t=43 d 时,或者在开挖面后方4 倍洞跨处,围岩的应力释放率接近于1,其空间约束效应基本消失;侯公羽等[17]认为,空间约束效应基本消失在开挖面后方5 倍洞跨处。因此,在0~43 d内(或者在4~5 倍洞跨范围内),需考虑空间约束效应对围岩应力重分布的影响,建议选取式(8)、(9)、(11)和式(16)、(17)、(19)计算。若t>43 d(或者支护结构的架设滞后于开挖面的推进,架设在4~5 倍洞跨范围外),则架设处围岩应力重分布已经完成,支护结构只能支护到围岩的蠕变变形,解析式不需要考虑pi作用。若使洞周面力pi=0,根据上述的解析思路可得围岩蠕变初始应力场,具体如下:
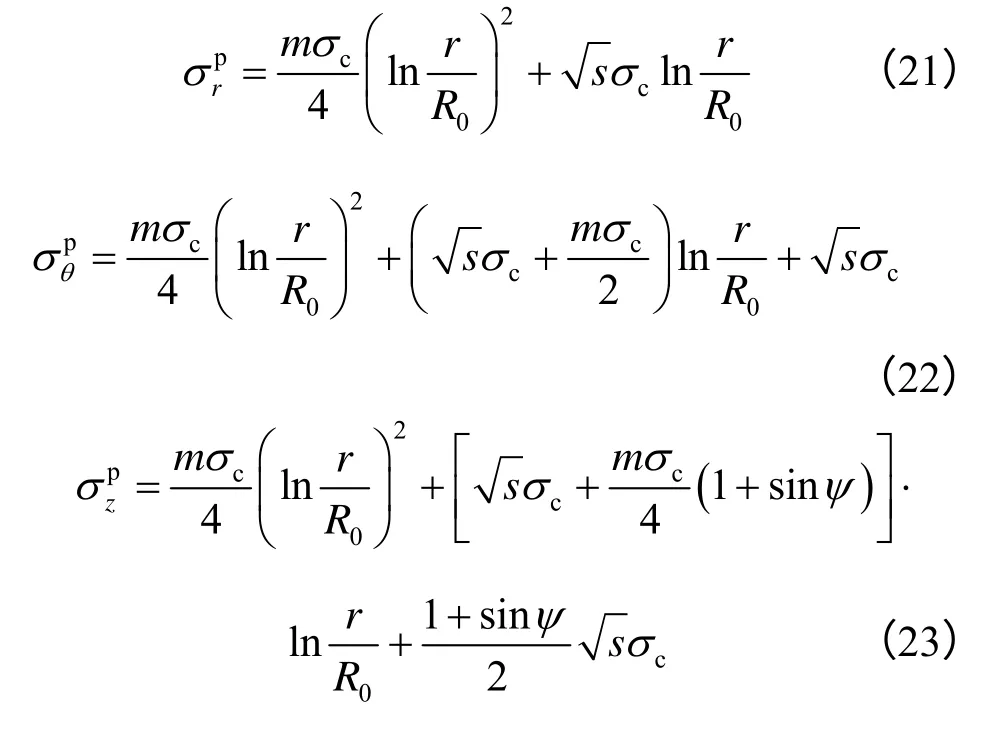

4 隧洞围岩非线性蠕变位移解
在解析中,假设应力重分布完成后应力场恒定。从以上各式可知,围岩内部偏应力Sij≠0;在偏应力作用下围岩将产生随时间增加的蠕变变形。
4.1 黏弹性区
由基本假设(3)可知,围岩黏弹性区应变含弹性应变和黏弹性应变。在非线性蠕变模型中,当NVPB 部分不参与蠕变时,模型将退化为含Hooke体和广义Kelvin 体的线性黏弹性蠕变模型,可充分反映围岩黏弹性区蠕变特性。在形式上等价于Sij≤σs情况。隧洞围岩蠕变符合空间轴对称假设,因此,几何方程 εθ=u/r、εr=du/dr 成立。
将式(16)、(17)、(19)代入式(4)、(5),再代入式(2),并结合/r 可得

4.2 黏塑性区
由基本假设(3)可知,围岩黏塑性区应变含弹性应变、黏弹性应变和黏塑性应变。相应地,蠕变模型由Hooke 体、广义Kelvin 体和NVPB 构成。
在黏塑性区,随着蠕变的进行,围岩裂隙发展并张开,使扩容效应增大。因此,黏塑性区蠕变位移的确定采用非关联流动法则,结合几何方程有
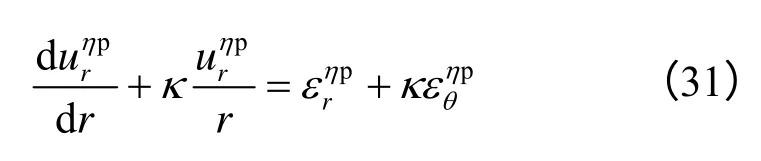
将式(2)代入式(31),可得

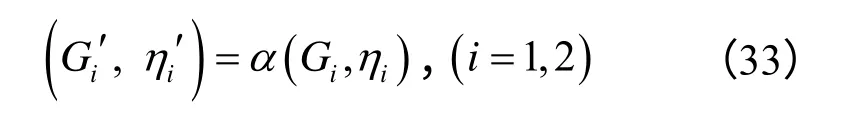
将式(8)、(9)、(11)代入式(4)、(5),再代入式(32),并结合边界条件,可得
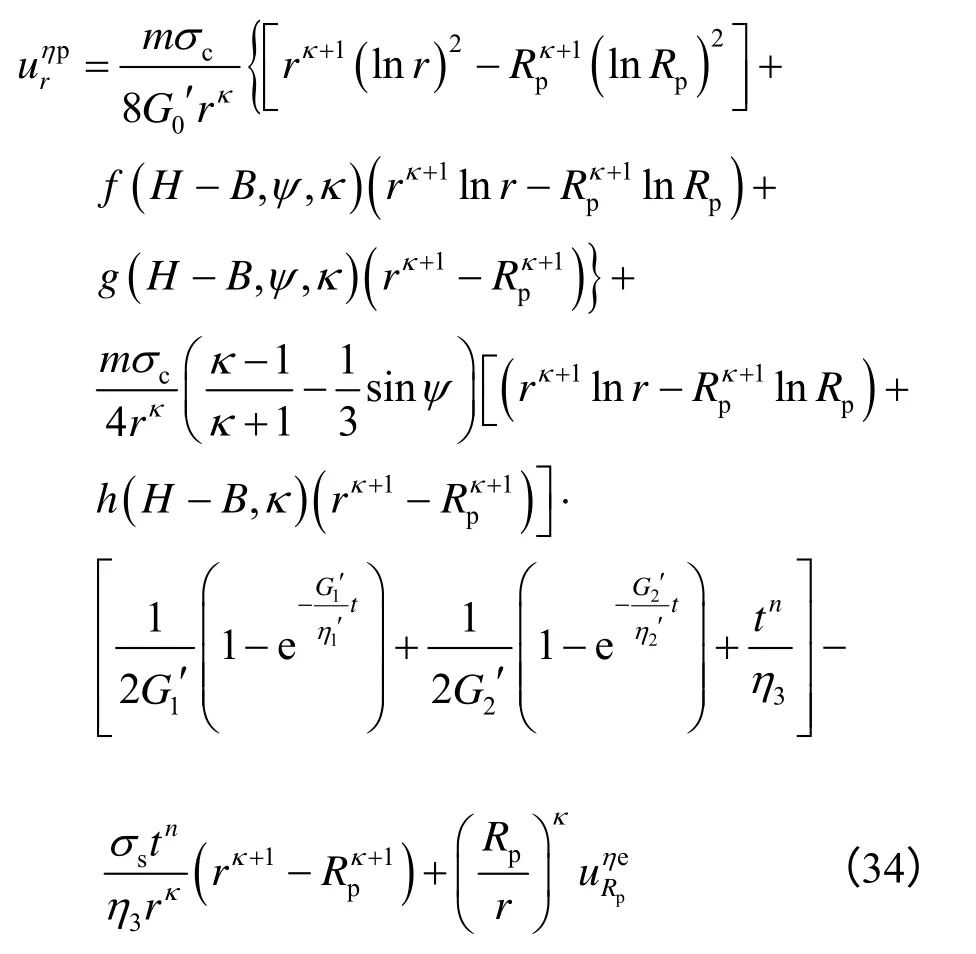
随着掌子面推进,隧洞内壁出现了自由面,围岩黏弹、黏塑性区均产生向内的位移。因此,黏塑性区总蠕变位移urcp,应包含黏弹性区产生的蠕变量。同时,考虑原岩应力作用下产生的初始地层位移u0。计算公式如下:
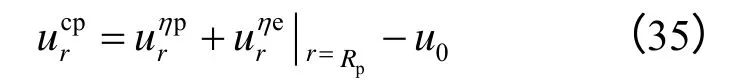

其中,材料函数如下:

若不计洞周面力影响,则把pi=0 代入材料函数式(37)~(39)可得结果。
5 分析与讨论
5.1 NVPB 参数η3和n
河海模型含7 个蠕变参数,因为参数众多,这里仅选取可充分反映围岩蠕变加速特性的NVPB 蠕变参数η3和n 进行分析。采用文献[18]的绿片岩蠕变参数进行分析,详见表1。影响围岩应力分布的相关参数取值:m=15,s=0.8,R0=3 m,φ=25°,ψ=10°,μ=0.25,α=0.8,pi=0.8 MPa,p0=40 MPa,σc=45 MPa;根据文献[19]确定σs=0.8,σc=36 MPa。

表1 绿片岩蠕变参数[18]Table 1 Creep parameters of green schist[18]
图4 给出了NVPB 蠕变参数η3和n 影响下绿片岩隧洞洞壁蠕变特征曲线。容易发现,在高地应力作用下,采用非线性蠕变模型可获得蠕变全过程曲线。如图所示,蠕变衰减及稳定阶段产生的位移量很小,一旦进入加速阶段,洞壁位移呈现出非线性剧烈增长,故在蠕变全过程曲线中往往难以体现出前两个阶段的蠕变规律(下同)。随着蠕变指数n增大和黏滞系数η3减小,围岩蠕变行为逐渐由黏弹性向黏弹塑性过渡。可见,参数η3和n 对隧洞围岩蠕变规律影响极大,决定了其是否进入加速阶段以及出现该阶段的时间,进而决定了隧洞围岩临崩预报工作的开展。因此,开挖岩石蠕变参数的辨识准确性应引起工程实践者的重视。
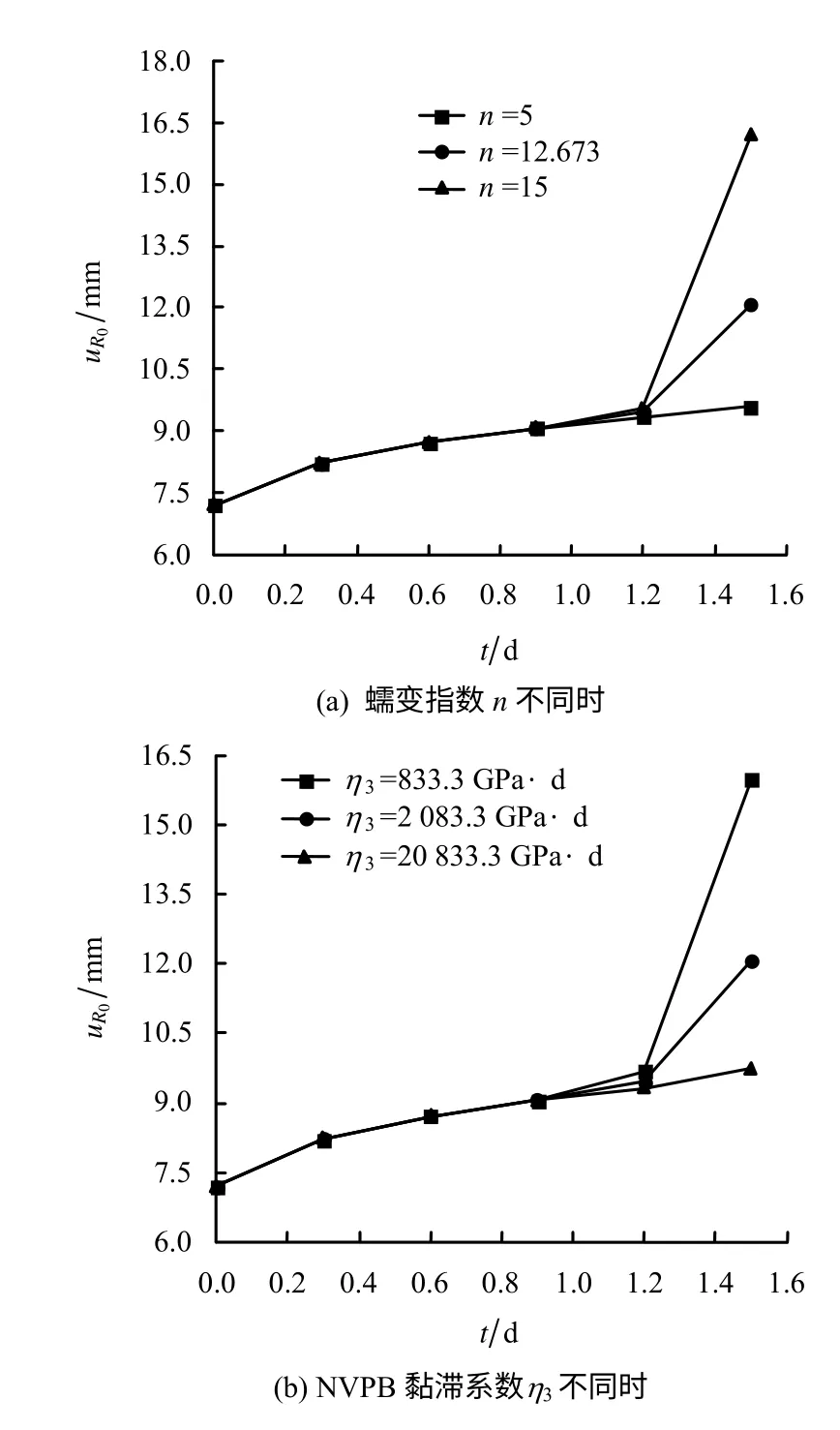
图4 绿片岩隧洞洞壁蠕变特征曲线Fig.4 Creep curves of tunnel wall in green schist
5.2 洞周面力
计算参数与上述一致,这里洞周面力pi分别取为0.0、0.8、1.6 MPa。为了突出蠕变衰减及稳定阶段,图5 只给出pi=0.8 MPa 时1.5 d 内隧洞洞壁蠕变特征曲线。如图所示,随着m 值增大,洞壁位移明显减小,这在加速蠕变阶段尤为突出,表明围岩软硬程度对洞壁位移影响较大,岩体越软,洞壁位移越大。图6 给出了洞周面力及m 值影响下围岩蠕变全过程的洞壁位移差值曲线;[Δu1]和[Δu2]是以pi=0.8 MPa为基准,洞周面力减至0.0 MPa和增至1.6 MPa 时的洞壁位移差值函数。由分布象限可知,[Δu1]>0 且[Δu2]<0,表明随着洞周面力pi增大,洞壁蠕变位移减小。当m=7,t=2.1 d 时,[Δu1]-[Δu2]=76.4-(-62.5)=138.9 mm,即洞周面力由0.0 MPa 增大到1.6 MPa 时位移差值接近于14 cm;发展此差值位移量需要一定时间,可见洞周面力对加速蠕变阶段的出现起到一定的延缓作用。由图6 可知,洞周面力对围岩蠕变的影响主要体现在加速阶段,[Δu1]+[Δu2]≠0,蠕变具有一定非线性特征。

图5 pi=0.8 MPa 时隧洞洞壁蠕变特征曲线Fig.5 Creep curves of tunnel wall with pi=0.8 MPa
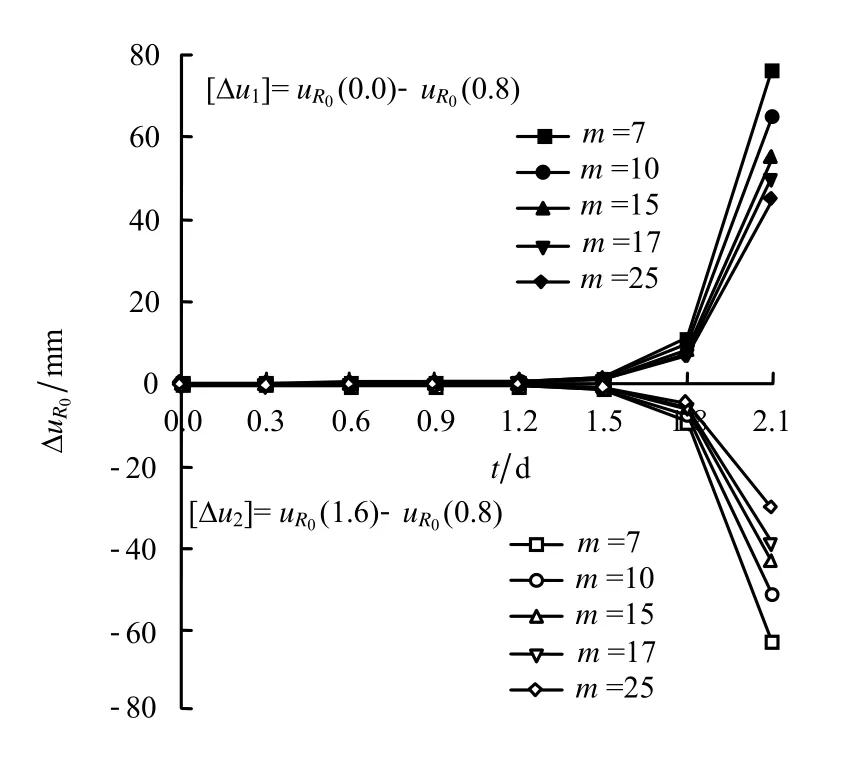
图6 洞周面力及材料参数敏感性分析Fig.6 Sensitivity analysis of surface force around tunnel and material parameter
5.3 扩容角
计算参数与上述一致,扩容角ψ 分别取为0°、10°、20°和30°。图7 给出了ψ=10°时隧洞洞壁蠕变特征曲线。容易发现,图7与图5 所得规律一致,岩体越软,洞壁位移越大。图8 给出了扩容角及m值影响下围岩蠕变全过程的洞壁位移差值曲线。[Δu10]=uR0(10°)-uR0(0°),表示以ψ=10°为基准,扩容角减至0°时的洞壁位移差值函数;[Δu12]和[Δu13]曲线簇意义等同,即为扩容角增至20°和30°时的洞壁位移差值函数。如图所示,[Δu10]>0 且[Δu13]<[Δu12]<0,表明随着扩容角ψ 增大,洞壁蠕变位移增大,这与扩容的实际作用相符。另外,扩容角对围岩蠕变的影响也主要体现在加速阶段,这是围岩蠕变加剧扩容效应的结果。当m 值取值较小,即岩体较软 时,[Δu10]+[Δu12]≠0 且[Δu13]-[Δu12]+[Δu10]≠0,更能说明深埋隧洞围岩蠕变的非线性特征。
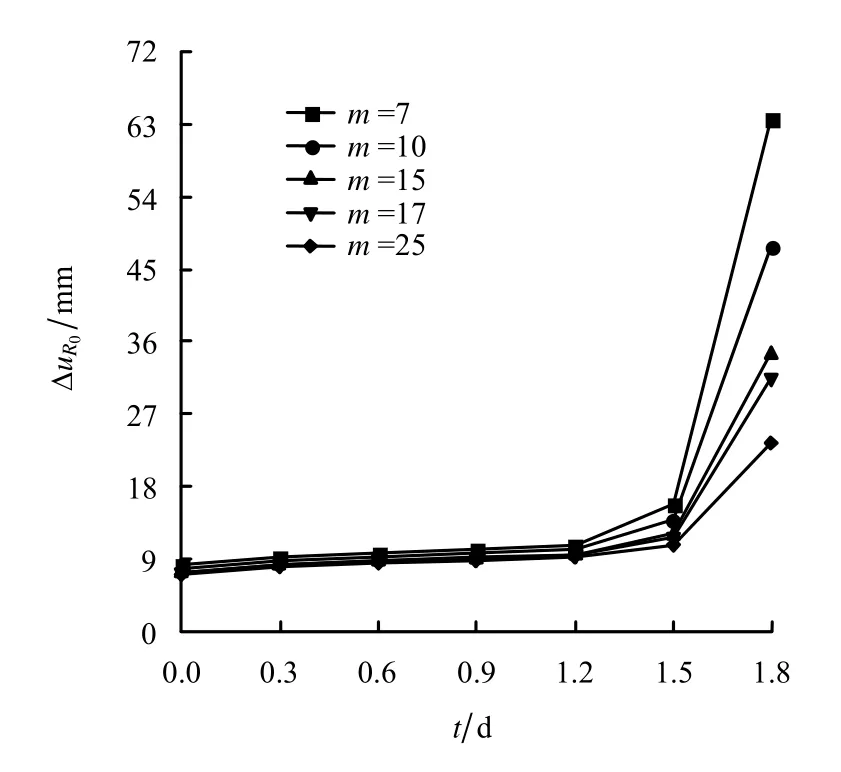
图7 ψ=10°时隧洞洞壁蠕变特征曲线Fig.7 Creep curves of tunnel wall with ψ=10°
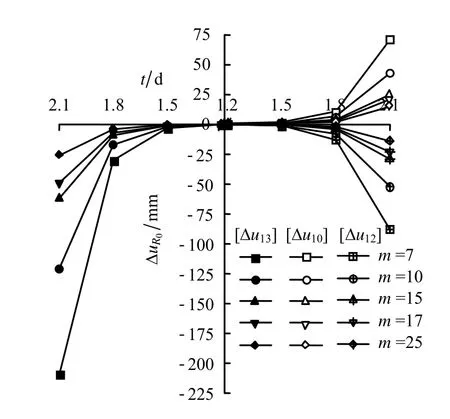
图8 扩容角及材料参数敏感性分析Fig.8 Sensitivity analysis of the dilatancy angle and material parameter
6 结 论
(1)在高地应力作用下,采用非线性蠕变模型描述深埋隧洞围岩蠕变问题可获得蠕变全过程曲线,随着NVPB 蠕变指数n增大和黏滞系数η3减小,围岩蠕变行为逐渐由黏弹性向黏弹塑性过渡。
(2)材料参数m 值越小,岩体越软,洞壁蠕变位移量越大,且蠕变行为更多体现为非线性特征。洞周面力在一定程度上可以减小洞壁位移,对加速蠕变阶段的出现起到一定的延缓作用;扩容角越大,洞壁位移就越大,对围岩长期稳定不利。
(3)深埋隧洞围岩非线性蠕变位移是一个多参数函数,其中岩石蠕变参数、洞周面力 pi、扩容角ψ与m 值等参数的准确获得对围岩临崩预报工作的开展具有重要意义。
本文获得的理论解仍有待结合实际工程作进一步验证和完善。
[1]陈宗基,康文法.岩石的封闭应力、蠕变和扩容及本构关系[J].岩石力学与工程学报,1991,10(4):299-312.TAN Tjongki,KANG Wen-fa.On the locked in stress,creep and dilatation of locks,and the constitutive equations[J].Chinese Journal of Rock Mechanics and Engineering,1991,10(4):299-312.
[2]DAEMEN K,JAAK J.Tunnel support loading caused by rock failure[R].Omaha:Geology,Soils,and Materials Branch,Missouri River Division,Corps of Engineering,1975.
[3]孙钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999.
[4]于学馥,郑颖人,刘怀恒,等.地下工程围岩稳定分析[M].北京煤炭工业出版社,1983.
[5]NOMIKOS P,RAHMANNEJAD R,SOFIANOS A.Supported axisymmetric tunnels within Linear viscoelastic Burgers rocks[J].International Journal of Rock Mechanics and Rock Engineering,2011,44(5):553-564.
[6]SULEM J,PANET M,GUENOT A.An analytical solution for time-dependent displacements in a circular tunnel[J].International Journal of Rock Mechanics and Mining Sciences &Geomechanics Abstracts,1987,24(3):155-164.
[7]FAHIMIFAR A,TEHRANI F M,HEDAYAT A,et al.Analytical solution for the excavation of circular tunnels in a visco-elastic Burger’s material under hydrostatic stress field[J].Tunnelling and Underground Space Technology,2010,25(4):297-304.
[8]卢爱红,茅献彪,彭维红.软岩巷道的弹-黏塑性分析[J].采矿与安全工程学报,2008,25(3):313-317.LU Ai-hong,MAO Xian-biao,PENG Wei-hong.Elasto-viscoplasticity analysis of soft rock tunnel[J].Journal of Mining and Safety Engineering,2008,25(3):313-317.
[9]FRITZ P.An analytical solution for axisymmetric tunnel problems in elastoviscoplastic media[J].International Journal for Numerical and Analytical Methods in Geomechanics,1984,8(4):325-342.
[10]卞跃威,夏才初,肖维民,等.考虑围岩软化特性和应力释放的圆形隧道黏弹塑性解[J].岩土力学,2013,34(1):211-220.BIAN Yue-wei,XIA Cai-chu,XIAO Wei-min,et al.Visco-elastoplastic solutions for circular tunnel considering stress release and softening behaviour of rocks[J].Rock and Soil Mechanics,2013,34(1):211-220.
[11]余东明,姚海林,段建新,等.考虑中主应力和剪胀的深埋圆形隧道黏弹塑性蠕变解[J].岩石力学与工程学报,2012,31(增刊2):3586-3592.YU Dong-ming,YAO Hai-lin,DUAN Jian-xin,et al.Visco-elastoplastic creep solutions to deep circular tunnels considering intermediate principal stress and shear dilatancy[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(Supp.2):3586-3592.
[12]STERPI D,GIODA G.Visco-plastic behaviour around advancing tunnels in squeezing rock[J].Rock Mechanics and Rock Engineering,2009,42(2):319-339.
[13]徐卫亚,杨圣奇,褚卫江.岩石非线性黏弹塑性流变模型(非线性蠕变模型)及其应用[J].岩石力学与工程学报,2006,25(3):433-447.XU Wei-ya,YANG Sheng-qi,CHU Wei-jiang.Nonlinear viscoelasto-plastic rheological model(Hohai model) of rock and its engineering application[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(3):433-447.
[14]齐亚静,姜清辉,王志俭,等.改进西原模型的三维蠕变本构方程及其参数辨识[J].岩石力学与工程学报,2012,31(2):347-355.QI Ya-jing,QIANG Qing-hui,WANG Zhi-jian,et al.3D creep constitutive equation of modified Nishihara model and its parameters identification[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(2):347-355.
[15]闫长斌,徐国元.对H-B 公式的改进及其工程应用[J].岩石力学与工程学报,2005,24(22):4030-4035.YAN Chang-bin,XU Guo-yuan.Modification of Hoek-Brown expressions and its application to engineering[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(22):4030-4035.
[16]余东明,姚海林,卢正,等.考虑中间主应力的横观各向同性深埋圆隧弹塑性解[J].岩土工程学报,2012,34(10):1850-1857.YU Dong-ming,YAO Hai-lin,LU Zheng,et al.Elastoplastic solutions to deep-buried circular tunnels in transversely isotropic rock masses considering intermediate principal stress[J].Chinese Journal of Geotechnical Engineering,2012,34(10):1850-1857.
[17]侯公羽,牛晓松.基于Levy-Mises 本构关系及Hoek-Brown 屈服准则的轴对称圆巷理想弹塑性解[J].岩石力学与工程学报,2010,29(4):765-777.HOU Gong-yu,NIU Xiao-song.Perfect elastoplastic solution of axisymmetric circular openings in rock mass based on Levy-Mises constitutive relation and Hoek-Brown yield criterion[J].Rock and Soil Mechanics,2010,29(4):765-777.
[18]徐卫亚,杨圣奇,谢守益,等.绿片岩三轴流变力学特性的研究(II):模型分析[J].岩土力学,2005,26(5):693-698.XU Wei-ya,YANG Sheng-qi,XIE Shou-yi,et al.Investigation on triaxial rheological mechanical properties of green schist specimen(II):Model analysis[J].Rock and Soil Mechanics,2005,26(5):693-698.
[19]张清照,沈明荣,丁文其.锦屏绿片岩力学特性及长期强度特性研究[J].岩石力学与工程学报,2012,31(8):1642-1649.ZHANG Qing-zhao,SHEN Ming-rong,DING Wen-qi.Study of mechanical properties and long-term strength of Jinping green schist[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(8):1642-1649.
