关注生成资源 演绎精彩课堂

◎福建省福州市亚峰中心小学 余尔真

关注生成资源 演绎精彩课堂

◎福建省福州市亚峰中心小学 余尔真

教学活动是师生互动，共同发展的过程。教师应在精心预设的基础上，关注课堂生成的有效资源，通过预设陷阱、把握分歧、捕捉亮点、善待错误、活用意外资源这五种策略来展现师生智慧互动的火花，演绎精彩的教学，让数学课堂焕发出生命的活力。

生成资源；精彩课堂；策略

《义务教育数学课程标准（2011年版）》指出：“教学活动是师生积极参与、交往互动、共同发展的过程。”而在师生、生生参与、互动、发展的过程中往往会动态生成许多新的资源——新情境、新问题、新思路、新方法、新结果等。我们知道成功的课堂不仅在于教师能顺利地执行预案，更在于执行预案过程中能正确关注课堂动态生成的资源，因势利导，适时调整预案，演绎精彩的课堂。下面笔者结合教学实践经验，谈谈以下五种有效策略。

一、欲擒故纵——预设陷阱资源，诱导冲突

欲擒故纵，“纵”是手段，“擒”才是目的。数学课堂教学中的“欲擒故纵”是指教师在教学预设时，根据学生的思维定势，故意设置陷阱，将学生引向错误，诱导冲突。再通过教师的引导，让学生自主学习、合作探究错误的原因，得出正确的结论，这样便能呈现出理想的教学效果。

如教学五年级“3的倍数的特征”时，教师让学生用1、3、6组成不同的整数，并判断哪些数分别是2、5、3的倍数。因为学生已经掌握了2、5的倍数的特征，所以对于2、5的倍数，对答如流。但哪些数是3的倍数呢？多数学生也认为个位上的数是3的倍数，这个数就是3的倍数，所以大多数同学同意3、6、13、16、36、63、136、163、316、613这些数是3的倍数。

师：你们是怎么判断的？

生1：这还不简单，个位上的数是3的倍数这个数就是3的倍数。

师（神秘）：是这样的吗？

生2：不对不对，我发现13、16个位上的数是3的倍数，13、16却不是3的倍数。

（学生炸开了锅，教师故作深沉）

师：怎么回事呢？那3的倍数的特征能不能看个位？

生（齐）：不能。

师：到底什么样的数才是3的倍数呢？

通过自主发现、小组讨论、计算验证之后，学生终于知晓3的倍数的特征：各位上的数的和是3的倍数。

正是教师预设陷阱，故意将学生引向错误，引发学生“上当”，激发了学生强烈的探究欲望，自主寻找到正确答案，轻而易举地完成了教学任务。

二、顺水推舟——把握分歧资源，引发思辩

在教学活动中，学生经常会出现不同意见，教师可以顺水推舟，组织学生辩论解决分歧。这样既尊重了学生的个性化理解，又能引发学生思考，最后取得共识。

如，在教学四年级数学广角“烙饼问题”时，教师课件出示关键信息：一个锅每次最多只能烙2张饼，两面都要烙，每面3分钟。通过学习学生明确了烙1张饼最快需要6分钟，烙2张饼最快也要6分钟之后，教师提出烙3张饼最快需要几分钟时，有的学生认为最快需要12分钟，有的学生认为最快只要9分钟，全班同学很自然地分成了两个阵营。

师：老师最欣赏同学有不同的声音了？咱们开个辩论会吧！请两方各选派一位代表，阐述观点，让大家信服好吗？（经过准备，小小辩论会开始了。）

代表1（在黑板上边摆边说）：像这样先烙2张——6分钟，再烙1张——6分钟，不是12分钟吗？

代表2（不甘示弱）：为什么烙2张饼和1张饼都要用6分钟呢？可以先烙第1、2张饼的正面需要3分钟；再烙第1张饼的反面、第3张饼的正面需要3分钟；最后烙第2、3张饼的反面需要3分钟，一共不是9分钟吗？

代表1（不服）：我觉得12分钟也是可以的。

代表2：你那样烙就不是最省时间了。要想最省时间锅里必须每次总烙2张饼，别让锅空着。

师：好，看来要最省时间关键是不能让锅空着！

教师面对课堂生成的分歧资源，没有简单判断是非，而是通过组织一场异彩纷呈的辩论大赛，聚焦“最省”；经过双方的一场唇枪舌剑之后，领会“最省”，这样，学生学得兴趣盎然，结论得出便水到渠成。

三、另辟蹊径——捕捉亮点资源，激活思维

课堂上亮点资源不容忽视，这些亮点往往是来自于学生独立的思考、精彩的对话、创意的见解，稍纵即逝。这就需要教师善于捕捉，巧妙利用，激活学生的思维，收获意外的惊喜。

如，教学四年级“多边形内角和”时，教师出示例题：你们能想办法求出六边形的内角和吗？

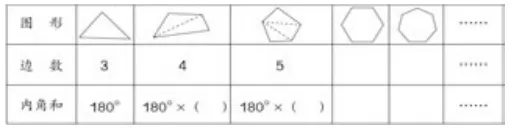
教师组织学生通过画一画，发现了每个多边形都可以分成“边数”－2个三角形，通过填一填、算一算，推导出多边形的内角和＝180°×（边数－2）的结论，从而得到了六边形的内角和180°×（6－2）=720°。

可是有同学提出这样想太麻烦的看法。教师立即让他走上讲台进行讲解，只见他在黑板上边画边说：“我在这个六边形中随便点上一个点，连接每个顶点，把这个六边形分成6个三角形，把6个三角形的内角和加起来再减去中间的一个周角不就是六边形的内角和吗？所以六边形的内角和是180°×6－360°＝720°。 ”

创意的见解，即时生成的亮点资源，起到“一石激起千层浪”的效果，便生发出四边形、五边形、七边形……内角和的求法，自然归纳得到多边形的内角和＝180°×边数－360°。

师：对比这两种方法，你发现了什么？这两种不同的分法得出的结论相同吗？

生1：这两种方法都是将六边形分成了三角形再计算。

生2：分法不同，求内角和的方法不同，但结果相同。

生3：其实这两种方法之间运用乘法分配律可以连接起来，180°×（边数－2）＝180°×边数－360°，所以用不同的分法得出的结论是相同的。

可见，正是这位同学的不经意的回答，生成“价值不菲”的教学资源。面对亮点资源，教师能静心倾听，及时捕捉，因势利导，以激活学生的思维，迸发智慧的火花。这样，既梳理了知识间的内在联系，又归纳了多边形内角和的求法，可谓一举两得！

四、拨乱反正——善待错误资源，点化困惑

课堂上可能出现亮点，也可能出现错误。课堂就是允许学生出错的地方。学生的错误往往呈现出学生的困惑，体现出教学重难点。因此，需要教师善待学生的错误，拨乱反正，巧妙地将错误资源转化为启迪思维的一个支点，使课堂峰回路转，同时学生的困惑也就迎刃而解！

如教学五年级数学广角“植树问题”时，教师为学生提供了如下情境：学校食堂门前有一条20米的小路，计划在小路的一边种些小树，每隔4米种一棵（两端种树），一共要种多少棵树？

生1（ 毫不犹豫）：20÷4=5（ 棵）。（ 部分同学点头）

生2（ 喃喃自语）：不对，不对，20÷4=5（ 段），不是5棵。

教师即兴采访了几个同学说说能种几棵树？并让学生说明理由，学生说来说去，说不清楚？

师：那怎么能让大家信服呢？

教师不做评判，引导学生画线段图，小组讨论汇报。

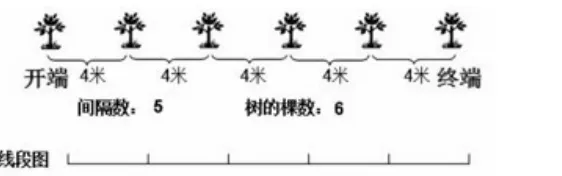
生3：我知道了，20米是总长度，4米是每段长度，20÷4=5（ 段）；

生4：因为两端种树，从图上可以看出棵树比段数多1，所以应该20÷4=5（ 段），5+1=6（ 棵）。

师：这是两端种树的情况？那如果一端种树呢？两端都不种树呢？

以上教学片段中，学生受限于段数、棵数之间概念的混淆，在思考的过程中出现一些错误是很正常的。教师没有马上纠正，从错误出发，通过画线段图，引导点拨，模糊的概念便一目了然。

五、随机应变——活用意外资源，化解僵局

教师总是希望课堂按照预设的教案执行，但课堂情况层出不穷，让人始料不及。因此，教学过程中难免有意外出现，这就需要教师具有驾驭课堂的能力，灵活处理意外资源，使教学效果锦上添花。

如教学四年级“解决问题”时，教师出示题目：旅行社推出“××风景区一日游”的两种价格方案，现有成人4人，儿童6人，选哪种方案合算？

选哪种方案合算？题目的意思很明显只能二选一，经过师生的共同努力发现，方案（一）：150×4+60×6=960（元）。方案（二）：100×10=1000（元）。基本达成了方案（一）更合算的共识。

可就在这时，有个学生坚决不同意方案一更合算。

生1：如果是我，一定是4个成人加上1个儿童凑成5人买团体票，剩下5个儿童买儿童票才最符合生活实际情况，也最便宜，总共只要100×5+60×5=800（元）。

同学们议论纷纷，以为大家都做错了。

师：大家同意这位同学的看法吗？（多数同学表示赞同）

生2（不服）：可题目中明明说选择哪一种方案更合算？也就是只能二选一啊！

生1（不甘示弱）：那就是这道题目有问题！因为生活中不可能有人这么买！两种方案综合运用，既没有违反旅行社规定，又便宜！何乐而不为？

越来越多的同学表示赞同。

师：老师很佩服这位同学的勇气，他很好的将数学知识应用于生活，同时敢于挑战课本，挑战权威。可是生2说的也对，那我们能不能将这道题目改一改，让题目更符合生活实际呢？

生3：应该将问题改为怎样买最优惠？

师：大家现在同意了吗？

生（齐）：同意！

综上所述，方案（一）明显是课本题目的最佳答案。但因为这位同学的“捣乱”，让课堂陷入僵局。不过教师没有批评学生，反而随机应变，成功化解僵局。通过质疑、辩论、修改题目等方式，生成出与生活紧密相关联的数学问题，既培养了学生敢于挑战教师乃至教科书权威的精神，又生动地诠释了数学服务于生活的理念。

总之，正如叶澜教授所言：“不去认真预设，那是不负责任；不善实时生成，那是不够优秀。”教师就需要在精心预设的基础上把握动态资源，及时捕捉，合理利用，巧妙点拨……演绎出精彩的数学课堂。

陈志华）