空间两点源的单脉冲测角极化响应研究∗

(国防科学技术大学,湖南长沙410073)

0 引言

雷达干扰与抗干扰的博弈一直是电子战中的热点领域,它事关武器系统的工作性能和生存能力,因此越来越受到重视。单脉冲雷达测角已是一种相对成熟的技术并广泛应用于高精度的雷达测角系统中,然而角度相近的两点源角度欺骗干扰却给单脉冲测角系统带来了严重威胁。当两点源处于同一角度分辨单元内而不可分辨时,雷达收到来自两个方向的来波,产生基于合成和差信号的单一角度测量值。多数情况下,角度测量值并未与其中任何一个不可分辨目标的角度相对应,进而破坏雷达角度跟踪系统。在现代电子战中,诸如拖曳式诱饵等一些干扰手段形成的两点源干扰极大地破坏了对真实目标的测角及跟踪的精准度[1],目前还未有很有效的对抗措施。而雷达对电磁波极化信息的提取和利用,已经被证明可以有效地提高抗干扰、目标检测和目标识别的能力[2]。充分挖掘极化信息为提高雷达的抗干扰和目标分辨能力开辟了有效途径。因此,提取和分析空间两点源在单脉冲测角系统中的极化响应,探究单脉冲系统在不同极化通道里得到的空间两点源角度测量值,对于抗两点源干扰有着极大的现实意义和应用价值。

针对两点源的响应问题,Ostrovityanov[3]详细推导了特定目标和天线极化下两点源的合成回波表达式,分析得出了雷达对线极化和随机极化两点源目标的归一化角闪烁误差,并得出上述两种情况下两点源目标的角闪烁偏差超出目标尺度之外的概率;针对单脉冲测角系统中两点源的不可分辨问题,Sherman等[4]研究了不可分辨目标的响应,指出在不可分辨的多点源目标情况下,和差信号之比为复数,并且分析了“复指示角”与两个目标回波和信号的幅度比、相对相位之间的关系;饶灿等[5]研究了主瓣干扰下自适应单脉冲测角方法;白渭雄[6]分别对相干干扰和非相干干扰两种情况下,两点源对单脉冲测角的影响进行了研究;李永祯等[7]从相干两点源在雷达测角系统不同极化通道的响应入手,构造了鉴别相干两点源角度欺骗干扰与雷达目标的鉴别统计量。但总体而言,现有的研究对空间两点源的情形考虑尚不全面,将单脉冲响应的幅度相位信息与极化信息结合起来的分析甚少。

本文从雷达极化理论出发,研究了空间两点源的单脉冲测角极化响应,重点研究了目标散射矩阵、目标回波幅度比和目标起伏特性对单脉冲雷达导引头的测角影响。得到了一些有意义的结论,为减弱或消除两点源对单脉冲测角系统的影响提供了有力支持。

1 单脉冲测角模型

在单脉冲测角系统中,设波束1和波束2的电压方向图分别为g1(θ)=g(θ0+θ),g2(θ)=g(θ0-θ),θ0为2个天线波束最大方向偏离天线瞄准方向的夹角,θ为目标偏离雷达瞄准方向的夹角,则和波束表示为gs(θ)=g(θ0-θ)+g(θ0+θ),差波束表示为gd(θ)=g(θ0-θ)-g(θ0+θ),如图1所示。

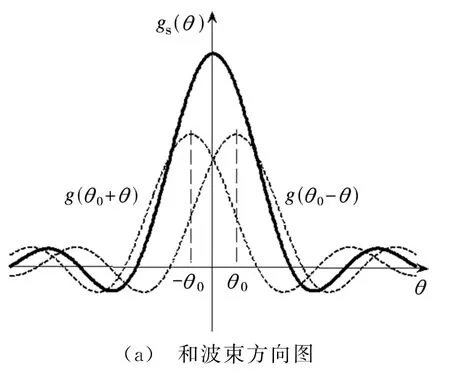
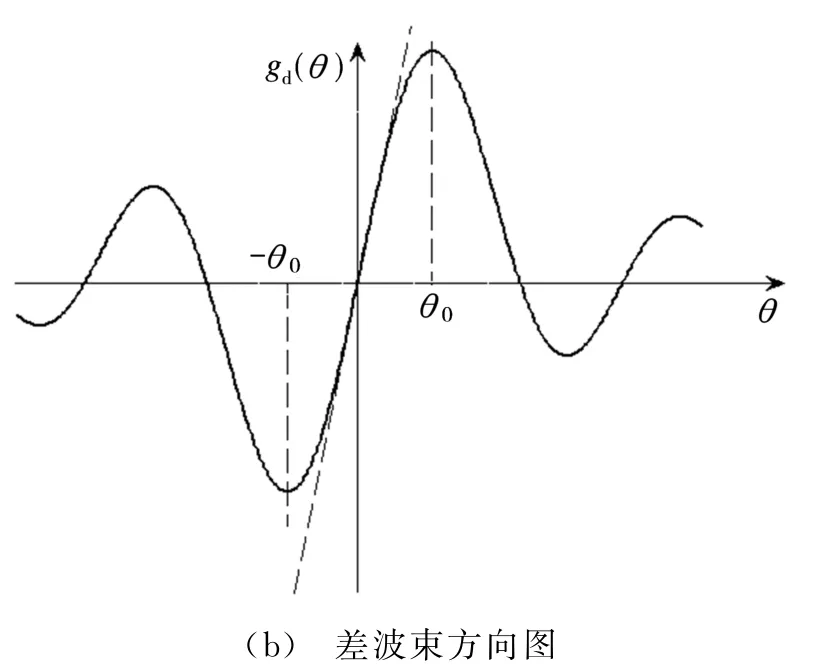
图1 单脉冲雷达方向图

假设目标在雷达接收天线端口处的后项散射波为e,和差通道的天线极化形式一致(hs=hd),则和差通道的接收电压可以分别表示为

利用和差波束天线接收信号可计算角度测量值为

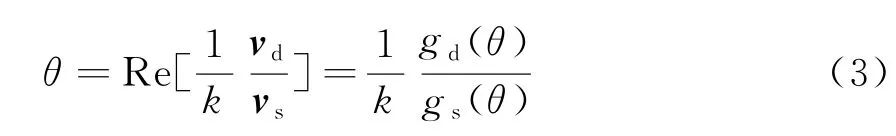
式中,k为单脉冲响应曲线斜率。

就测角的极化特性而言,由式(3)可以看出,对于单目标而言,其单脉冲测角与收发天线的极化形式无关,无论收发天线采取何种极化形式,角度测量值只与和差波束天线增益相关。而以下可以看到,与单目标的情形有所不同,空间两点源的测角结果则与收发天线极化形式密切相关。两点源的测角结果依赖于发射天线与接收天线的极化形式,具有极化敏感性。

设雷达的信号为A,则结合相干信号仿真和雷达极化理论易得[1],空间两个点源在雷达接收天线端口处的后向散射波[8]为

式中:gt为发射天线的方向图函数,两点源的入射信号的方向分别为θ1,θ2;S1,2为空间两个点源在当前姿态、当前频率下的极化散射矩阵,且对于互异性目标而言,表示发射天线的极化形式。

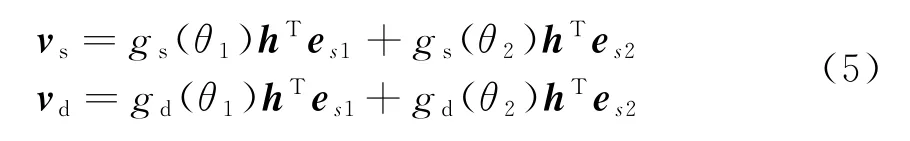
在单脉冲测角系统中,假设和差通道的天线极化形式一致(hs=hd=h),则和差通道的接收电压可以分别表示为gs(θ1,2),gd(θ1,2)分别为和差波束天线在该方位角上的增益。利用来自两点源和差波束天线接收信号可计算角度为

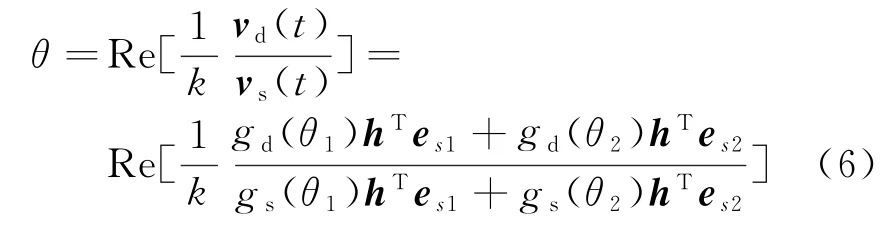
且对于每一个目标,有

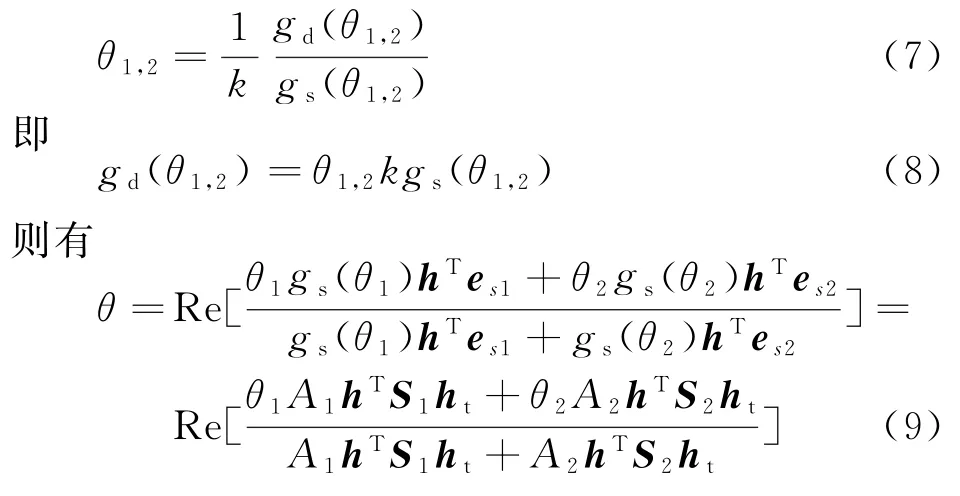
式中,A1=gs(θ1)gt(θ1)A,A2=gs(θ2)gt(θ2)A。从式(9)可以看出,对波束内空间两点源的角度测量值受两点的目标散射矩阵、收发天线的极化形式等因素影响,显现出一定的极化敏感性。也就是说,空间两点源的角度测量值与目标以及天线的极化特性密切相关。

2 目标散射矩阵结构对单脉冲测角的影响

目标的极化散射矩阵是一个由同极化分量和交叉极化分量组成的二阶矩阵,在H,V极化基下,目标散射矩阵表示为,它反映了目标后向散射回波和入射电磁波的各极化分量之间存在的线性关系。在入射电磁波的极化确定时,目标散射矩阵改变了目标散射回波的极化,进而影响了雷达接收天线对目标后向散射回波的接收电压。所以目标的极化特性很大程度上影响了两点源的测角情况。为更清楚地表现出目标散射矩阵的结构对单脉冲测角的影响,定义退极化比为目标散射矩阵的交叉极化分量与同极化分量之比。假设的退极化比。一般情况下,c1≪1。单脉冲雷达在单极化条件下采用同极化接收,不妨设ht=h=[hHhV]T,且‖ht‖=‖h‖=1。

情况1:当S2的各分量与S1成比例,即S2= αS1时,由式(9)易得

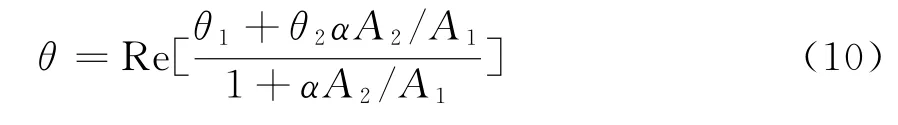
由于S2与S1成比例,空间两目标对于雷达照射波的变极化效果相同,只在幅度上相差一个系数α,所以来自空间两个点源的后向散射回波是同极化的,计算式(9)的分子分母约去了收发极化以及退极化比c1的影响,角度测量值只与两目标的回波增益比A2/A1和系数α有关。

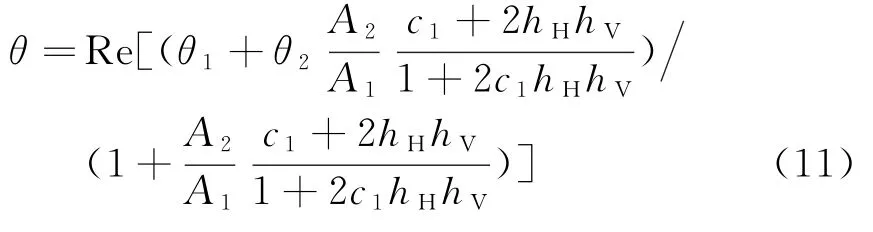
角度测量值与收发极化和c1值均有关系。图2反映了角度测量值随S1的退极化系数c1的变化趋势。θ1,θ2分别为0.2°和-0.2°。从图中可见,S2= αS1时,角度测量值不受散射矩阵结构改变的影响。当时,角度测量值与c1的取值有关,目标散射矩阵结构影响着空间两点源的测角。单极化条件下采用不同的极化通道角度测量值也会有所不同,但由式(11)中hH和hV的对称性可知,若采用常用的H极化收发或者V极化收发,测角情况相同,c1≪1情况下,两点近似认为,角度测量值都落在θ1=0.2°处。特别地,当c1=1时,S1=S2,角度测量值为(θ1+θ2)/2。

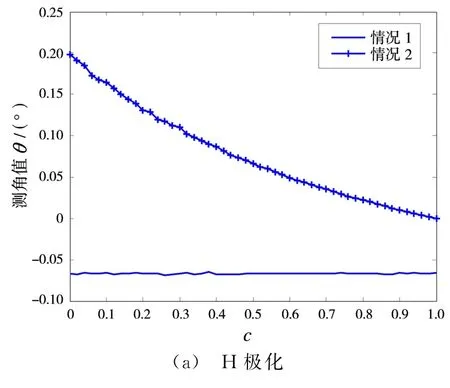
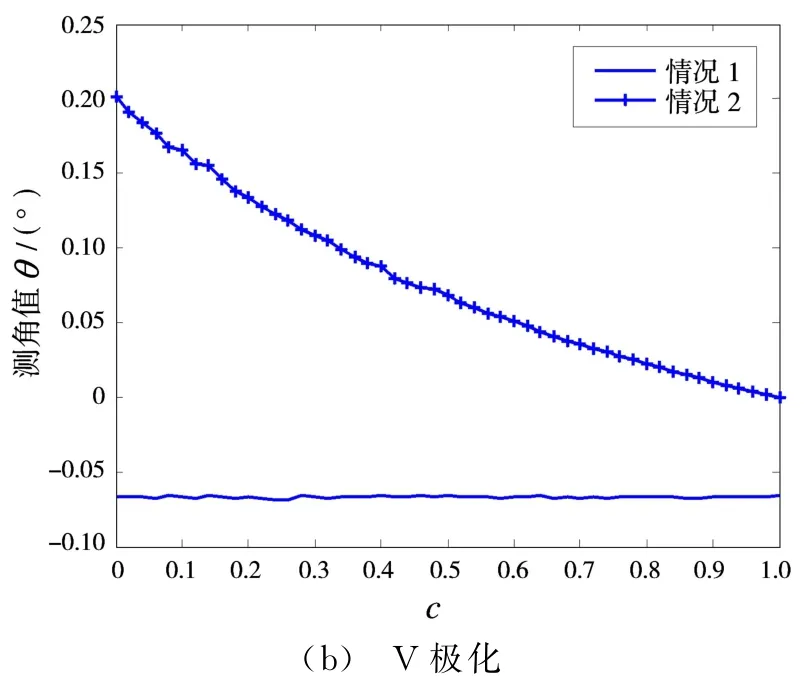
图2 目标散射矩阵对测角的影响

3 目标回波幅度比对单脉冲测角的影响

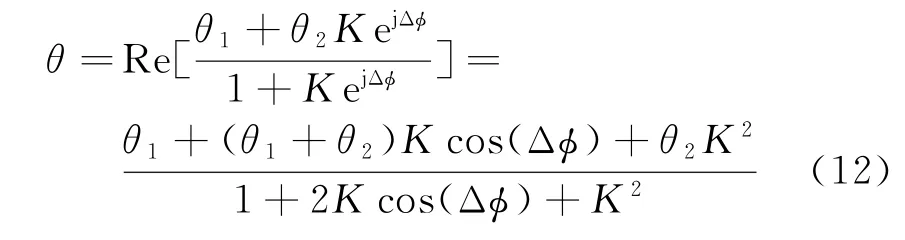
K值实际上反映了雷达接收两目标的和通道回波幅度之比,在目标散射矩阵一定的前提下,K值实质上由收发天线的极化形式决定。表1以S1=[1 0.2;0.2 0.7],S2=[0.6 0.3;0.3 0.4],θ1=-0.5°,θ2=0.5°为例,得到4种收发极化情况下的角度测量值。这表明不同收发极化得到的K值不同,进而角度测量值θ也会有所不同。

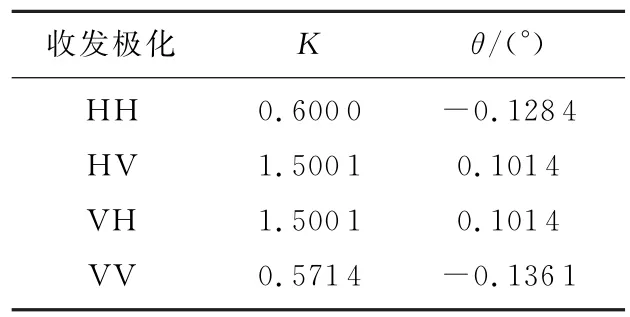
表1 收发极化对K值的影响

当Δϕ可控时,角度测量值可以由K值唯一确定。如图3所示,当K=0时,雷达只接收到来自点1的回波,测角指向θ1;当K=∞时,雷达只接收到来自点2的回波,测角指向θ2;特别地,当K=1且cosΔϕ≠π时,这时两点的回波幅度相等,角度测量值恒有同时,K值分布在某些区出两点源的尺度范围。若把θ1看作目标方向,把θ2看作干扰方向,可定义测角误差为|θ-θ1|。由式(12)得到

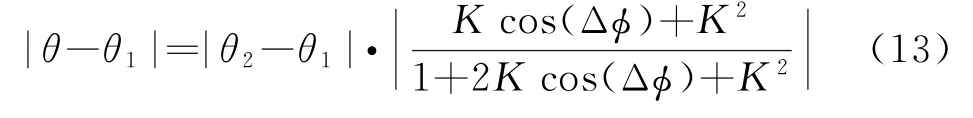
当K=0时,误差最小,此时接收不到来自干扰的回波,也即在接收极化与干扰极化正交时,具有最小的测角误差。

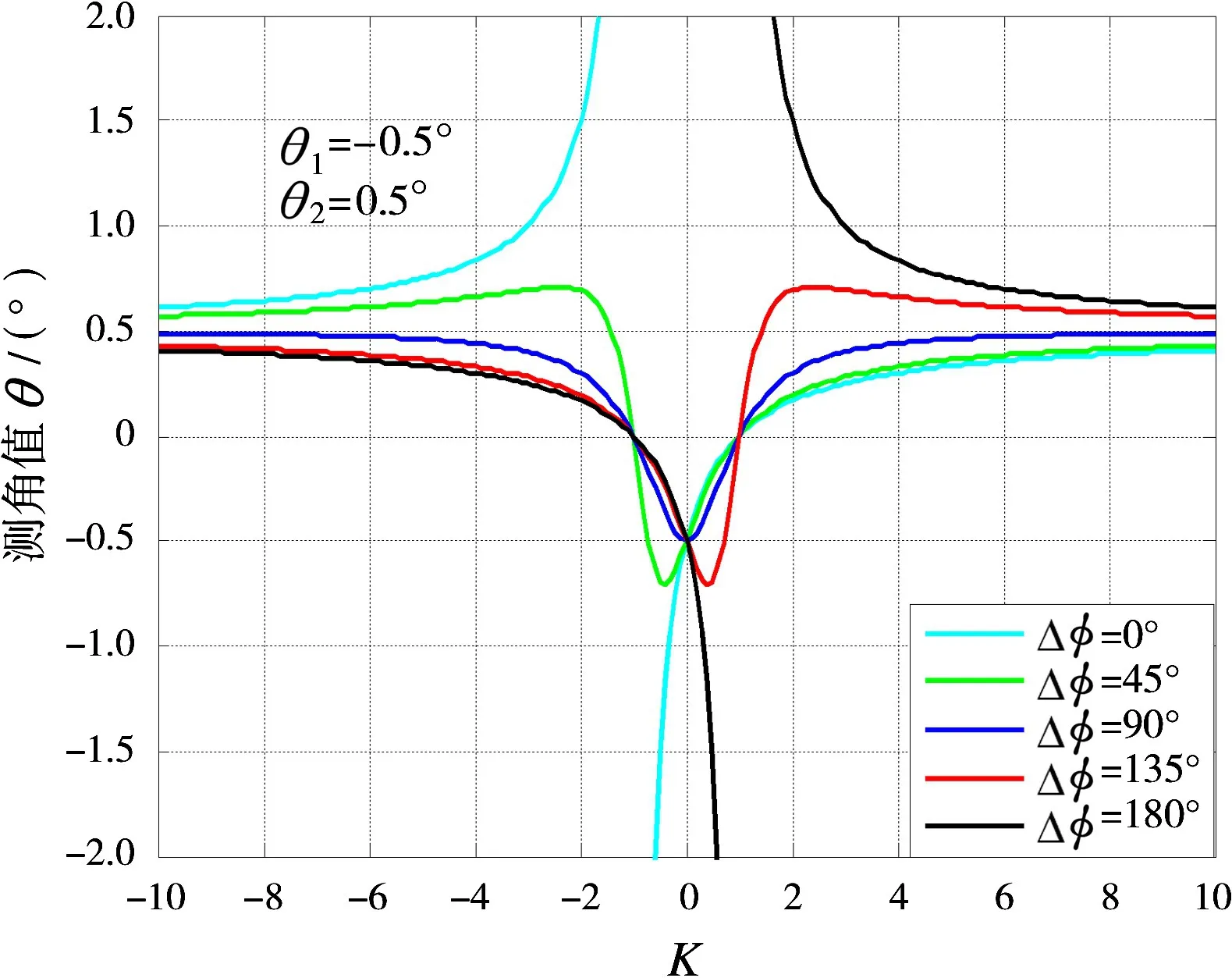
图3 角度测量值与K值的关系

而当Δϕ不可控时,可将两回波间的相位差Δϕ视为随机相差,在[0,2π]上均匀分布。根据Δϕ的分布,式(12)也可以改写为

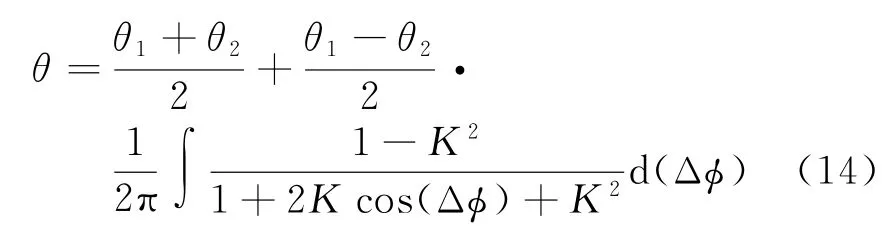
得出平均角度测量值有

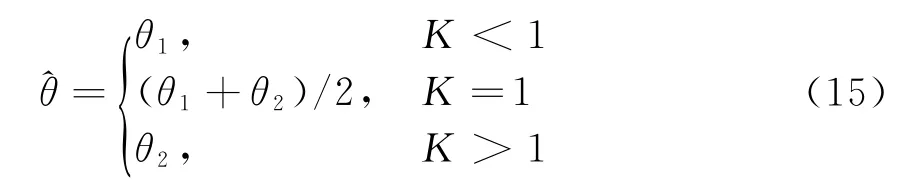
在这种情况下,若要角度测量值落在θ1上,只需K＜1。

若K值用极化比的形式表示出来将更有利于观察空间两点源测角与收发极化的关系。设E s1和E s2在(H,V)极化基下的极化比分别为ρ1和ρ2,雷达接收天线极化比为ρr,则其中A′1,2=gs(θ1,2)‖E s1,2‖。在目标和发射极化给定的情况下,采用变极化接收。根据雷达极化理论,接收天线极化比可表示为ρr=tanγejϕ,其中(γ,ϕ)为一对可以确定极化状态的极化相位描述子。仿真中,固定发射为H极化,在线极化轨道约束下改变接收极化(即改变参数γ)。蒙特卡洛仿真次数为100。图4(a)中两点源信号间相位差可控。角度测量值θ随γ而改变,θ既可以落在两点之间又可以在两点之外,当γ=135°时,θ=θ1= 0.2°,角度测量值θ不受θ2的影响,此时ρr= -1/ρ2。故在接收时尽量地使接收极化与干扰正交,可以减少测角误差。图4(b)中两目标信号间为随机相位差,当K＜1时,不受接收极化的影响,角度测量值总是指向回波幅度较大者θ1。

图4 两个不起伏目标

4 目标起伏特性对单脉冲测角的影响

以上分析都是假设目标不起伏。实际上目标的任何机动动作都会引起反射信号的变化,因而反射信号振幅表现为起伏的信号[9]。目标的起伏会对回波幅度比K值带来影响。由于K值只与后向散射回波和接收天线的极化状态有关,式(12)不仅可以用于无源目标情况,同样也可以用于干扰的情况。若考虑目标的起伏特性,根据两个目标的自身特性,本文把两点源分为3种情况展开研究:1)两个散射矩阵不起伏的目标;2)一个不起伏目标和一个干扰;3)一个起伏目标和一个干扰。受起伏特性影响,角度测量值为一随机变量,本文以θ的统计均值作为角度测量值^θ。一般而言,角度测量值由一般的表达式得出[10]:

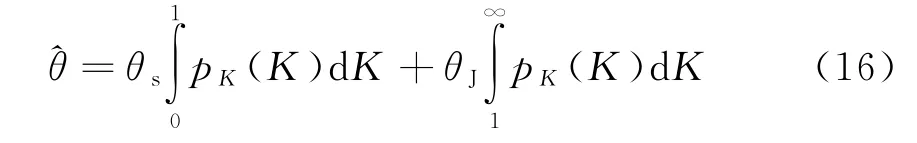
式中,K为雷达和通道接收干扰与目标的回波幅度之比,pK(K)为K的概率分布密度。

1)当两点源为两个不起伏目标时,角度测量值表达式如式(15)。

2)当两点源为一个不起伏目标和一个干扰时,假设干扰是高斯的,则干扰电压幅度服从瑞利分布,相位在[0,2π]上均匀分布,则角度测量值有

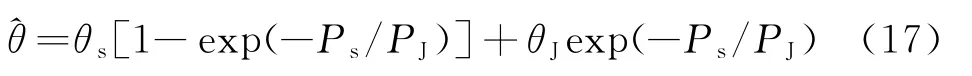
式中,Ps,PJ分别为目标和干扰在和通道接收的平均功率。

3)当两点源为一个起伏目标和一个干扰时,假设目标服从Swerling 1起伏模型,干扰目标的幅度服从瑞利分布,相位在[0,2π]上均匀分布,则角度测量值有

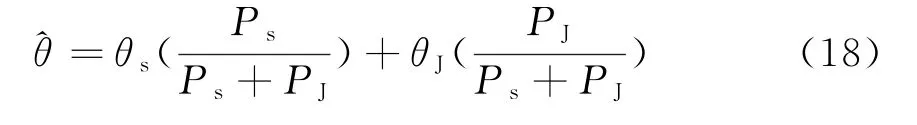
即对两点源的角度测量值总是指向两点源的功率质心。

图5中两图的干扰均为45°线极化,ρJ=1;图5(a)中目标不起伏,图5(b)中目标服从Swerling 1起伏模型。对比图4可知,目标的起伏使得单脉冲的测角结果随接收极化γ在两点源之间浮动,不同起伏规律的点源所造成的测角结果也有所不同,但角度测量值总是与两点源的功率质心相吻合。此外,γ的改变使得目标和干扰的接收功率发生变化,而测角误差与信干比Ps/PJ的趋势一致,信干比越大,误差越小。在信干比最大的γ=135°附近(ρr=-1)测角误差|^θ-θs|最小。同样此时有ρr=-1/ρJ,接收极化与干扰极化正交。

5 结束语

图5 目标起伏对测角的影响

本文分析了两点源在单脉冲测角系统中的极化响应,从极化的角度说明了目标散射矩阵、目标回波幅度比和目标起伏特性对单脉冲测角均会带来影响。目标散射矩阵的不同时,其测角的极化响应也会有差异。当两点源相位差可控时,角度测量值由两点散射回波幅度比K值决定。两点源相位差随机时,测角指向两点的平均接收功率质心。接收天线不同的极化状态很大程度上影响了单脉冲测角系统对两点源的测量,若两点之中一个视为目标另一个视为干扰,当ρr=-1/ρJ时,即接收天线与干扰互为交叉极化时,角度测量值为目标的方位角。影响空间两点源的测角因素分析为极化鉴别、极化对抗等领域提供了借鉴,为后续空间两点源抗干扰算法的研究奠定了基础。

[1]付孝龙,白渭雄,李兴成,等.基于复单脉冲比的拖曳式诱饵存在性检测[J].现代防御技术,2013,41(5): 129-133.

[2]李永祯,肖顺平,王雪松,等.雷达极化抗干扰技术[M].北京:国防工业出版社,2010:171-241.

[3]OSTROVITYANOV R V,BASALOV F A.Statistical Theory of Extended Radar Targets[M].Norwood,MA:Artech House,1985:193-233.

[4]SHERMAN S M,BARTON D K.单脉冲测向原理与技术[M].2版.周颖,陈远征,赵锋,等译.北京:国防工业出版社,2013:169-200.

[5]饶灿,李荣锋.主瓣干扰下多点约束自适应单脉冲测角方法[J].雷达科学与技术,2011,9(3):232-236. RAO Can,LI Rong-feng.Multipoint Constraint Adaptive Monopulse Estimation in the Presence of Mainlobe Jamming[J].Radar Science and Technology,2011,9(3):232-236.(in Chinese)

[6]白渭雄,唐宏,陶建峰.拖曳式诱饵对单脉冲雷达的干扰分析[J].电子信息对抗技术,2007,22(6):39-42.

[7]李永祯,胡万秋,程旭,等.相干两点源角欺骗干扰的极化鉴别方法研究[J].兵工学报,2013,34(9): 1078-1083.

[8]李永祯,胡万秋,陈思伟,等.有源转发式干扰的全极化单脉冲雷达抑制方法研究[J].电子与信息学报, 2015,37(2):276-282.

[9]方棉佳,吕涛.单脉冲和差波束测角的精度研究[J].雷达科学与技术,2013,11(6):645-649. FANG Mian-jia,LV Tao.Research on Precision of Angle Measurements in Monopulse Sum-Difference Beams[J].Radar Science and Technology,2013,11 (6):645-649.(in Chinese)

[10]KANTER I.Varieties of Average Monopulse Responses to Multiple Targets[J].IEEE Trans on Aerospace and Electronic Systems,1981,17(1):25-28.