基于协方差矩阵双层重构的稳健自适应单脉冲测角*

佘宏伟，晋良念,2

(1.桂林电子科技大学 信息与通信学院，广西 桂林 541004；2.广西无线宽带通信与信号处理重点实验室，广西 桂林 541004)

0 引 言

在现代的被动雷达角跟踪系统中，单脉冲技术通常被用来对目标信号进行角度估计。当存在主瓣干扰时，可以结合自适应波束形成技术在干扰位置形成零陷抑制，但这同时使得主波束方向图明显产生畸变，导致单脉冲比曲线严重失真，进而影响到被动雷达的测角精度及其跟踪性能。因此，提升单脉冲技术的干扰抑制能力和测角精度是当前亟待解决的一个关键问题。

针对单脉冲测角技术[1]在主瓣干扰下性能恶化的问题，众多学者在原有技术的基础上进行了深入研究和改进，随后提出了自适应单脉冲技术，但大多是基于单脉冲测角方法结合传统自适应波束形成而提出的。作为这类技术的关键环节，自适应波束形成基于相关的优化准则来处理阵列信号并获得最优权系数，从而达到抑制干扰和噪声并提高输出信干噪比(Signal-to-Interference plus Noise Ratio,SINR)的目的。在实际环境下的信号导向矢量和协方差矩阵与其相应真实值之间存在着失配问题，导致传统自适应波束形成的性能严重恶化，因此算法稳健性就成了提升自适应单脉冲技术性能的必然要求。文献[2]提出构造一个可变对角加载矩阵，减弱了高信噪比(Signal-to-Noise Ratio,SNR)下目标“自消”的现象，但同时也降低了干扰抑制能力。文献[3]提出了一种稳健Capon波束形成算法，通过不确定集约束导向矢量误差范围，但在导向矢量误差波动较大时算法性能大幅下降。文献[4]提出了利用Capon功率谱在非目标角度区域内构建环形不确定集，然后通过积分重构干扰加噪声协方差矩阵，提高了在阵列导向矢量失配下的干扰抑制能力，但是该方法计算冗余度极高。

针对上述问题，本文提出了一种协方差矩阵双层重构的稳健自适应单脉冲测角方法。先利用Capon功率谱估计目标导向矢量以求出干扰加噪声协方差矩阵的初始值，根据最小化干扰加噪声功率输出准则以及干扰导向矢量不确定集约束估计出干扰导向矢量及其信号功率，完成对干扰加噪声协方差矩阵的重构；通过Capon波束形成得到自适应和波束权重，然后按照设定的约束区间对俯仰角和方位角进行联合线性约束，并根据线性约束最小方差(Linearly Constrained Minimum Variance，LCMV)准则求出自适应差波束权重；最后根据自适应单脉冲比测得目标角度。该方法有效解决了传统自适应单脉冲方法干扰抑制能力差、测角精度低的问题，同时也明显改善了由于导向矢量和协方差矩阵失配导致波束形成性能恶化的问题，提升了算法的稳健性。

1 信号模型

考虑一个阵元数为M×N的矩形平面阵，如图1所示，阵列位于(x,y,z)坐标系的Y-Z平面上，法线方向为X轴。

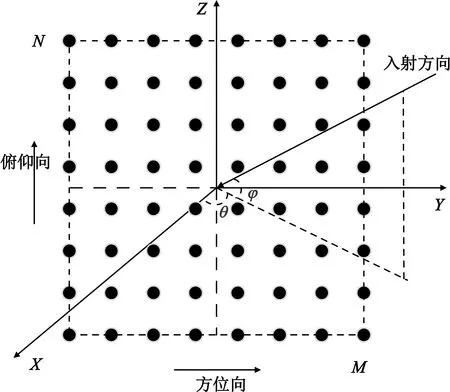
图1 矩形平面阵示意图

阵列被划分为L1×L2的子阵列，每个子阵列的阵元数为K1×K2，即得K1×L1=M和K2×L2=N。目标角度由方位角和俯仰角的角坐标(θ,φ)来定义，阵列输出x由目标回波、干扰J以及高斯白噪声n组成：

x=b·a(θ,φ)+J+n。

(1)

式中：b为复包络，与目标信号的相位和幅度相关；a(θ,φ)为导向矢量，即

(2)

式中：dy和dz分别表示沿Y轴和Z轴分布的阵元间距，λ表示载波波长。

基于子阵列的划分，将阵列输出x通过一个MN×L1L2的矩阵T等效转换为L1L2维向量z以作为子阵列的输出：

(3)

式中：Tu(或Tv)的第i列向量包含了用于方位维(或俯仰维)上对第i个子阵列内各个阵元的复数权重，⊗表示克罗内克积。

(4)

式中：(gi)k=ej2π(k-1)dysin θ0·cos φ0/λ，i=1,2,…,L1以及k=1,2,…,K1；(θ0,φ0)表示波束指向角。

(5)

式中：(hi)k=ej2π(k-1)dzsin φ0/λ，i=1,2,…,L2以及k=1,2,…,K2。

2 算法描述

当阵列信号仅由目标和噪声组成时，通常利用静态单脉冲比来估计目标角度(θ,φ)；而当阵列信号中存在主瓣干扰时，则采用自适应单脉冲比进行测角。假设目标位于主波束中心指向角(θ0,φ0)的附近，表示两者之间存在较小的偏转角Δθ和Δφ，即(θ,φ)=(θ0+Δθ,φ0+Δφ)，则对应于目标角度(θ0+Δθ,φ0+Δφ)的自适应单脉冲比可以表示为

(6)

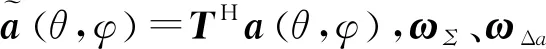
由于静态单脉冲比与偏转角近似线性关系，而为保证自适应单脉冲比与静态单脉冲比之间的近似性，也应满足如下条件[5]：

(7)

式中：r1是静态俯仰向单脉冲比斜率常数，r2和r3是静态方位向单脉冲比斜率常数。

结合式(1)和式(7)，所求自适应和差波束权重不仅需要最小化干扰及噪声功率，还需要保证主瓣干扰下自适应单脉冲比与静态单脉冲比之间的近似性。

2.1 协方差矩阵双层重构求解ωΣ

R=E[z·zH]=Rs+Rin。

(8)

(9)

式中：Nn表示快拍数。基于Capon波束形成求解自适应波束最优权重一般可表示为

(10)

假设目标角度大致位于区间ψ内，对该区间范围内的Capon功率谱积分得到

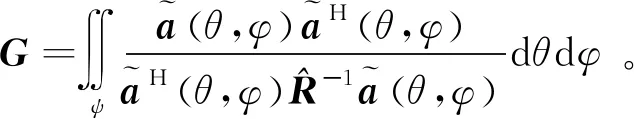
(11)

然后对G特征值分解，其最大特征值对应的特征向量作为目标导向矢量的估计值A0：

(12)

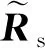
(13)

(14)

(15a)

(15b)

(16)

参数λ可由如下约束方程求解：

(17)

在估计出干扰导向矢量后，还需要估计干扰功率。通常目标加干扰协方差矩阵可表示为

(18)

(19)

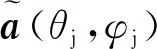
(20)

则干扰功率估计值为

(21)

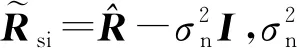
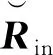
(22)

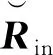
(23)

式中：ωqΣ=THa(θ0,φ0)。

2.2 联合线性约束求解ωΔa和ωΔe

常规自适应单脉冲技术虽然能在一定程度上抑制主瓣干扰，但也同时引起自适应单脉冲比严重失真，导致单脉冲测角性能急剧下降。针对这一问题，本节在自适应差波束形成的同时对方位向和俯仰向单脉冲比进行联合线性约束，从而避免单脉冲比产生严重失真。假设主波束指向为(θ0,φ0)，约束间隔设为(Δθ′,Δφ′)，同时为保证自适应单脉冲比与静态单脉冲比之间的近似性，满足式(7)所给条件，则对应于(θ0±Δθ′,φ0±Δφ′)的自适应单脉冲比表示为

(24)

将式(23)代入式(24)中来求解自适应差波束权重，通过展开处理可将上式表述为基于LCMV波束形成准则的优化问题：

(25)

(26)

约束矩阵C、约束响应Fa和Fe分别表示为

(27)

(28)

(29)

式(27)中的约束矩阵子向量由下式给出：

(30)

式(28)和式(29)中的约束响应子向量表示为

(31)

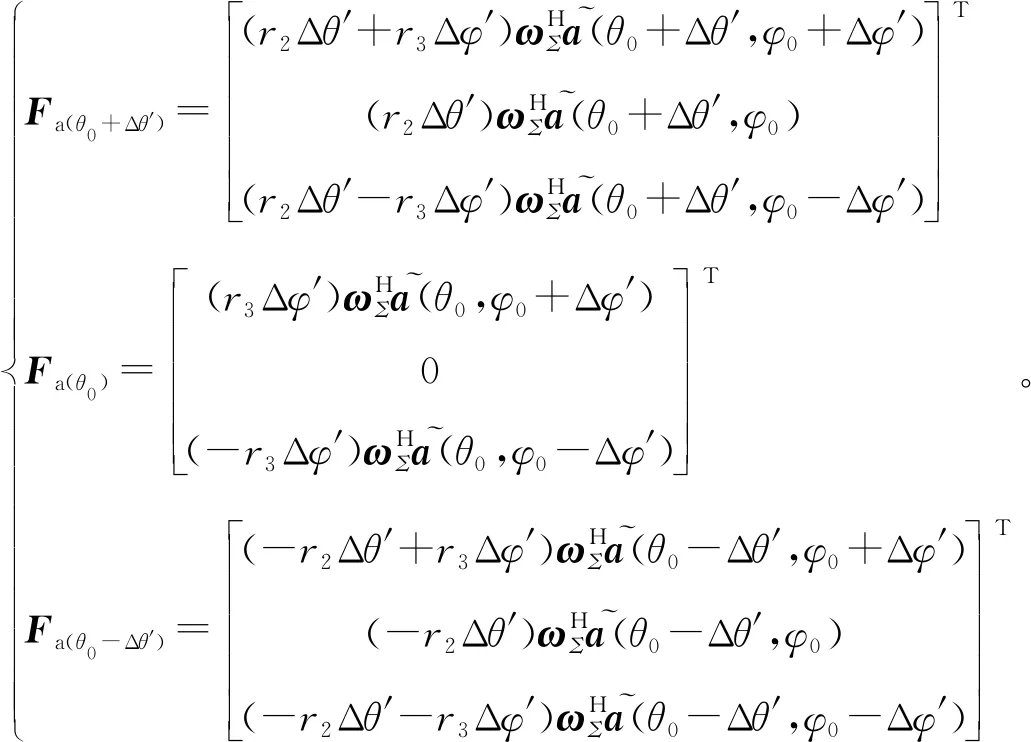
(32)

通过拉格朗日乘数法对式(25)和式(26)进行求解得到自适应差波束权重为

(33)

(34)

将求出的和差波束权重代入式(6)中，得到对应的自适应单脉冲比。根据式(7)中单脉冲比与偏转角之间的关系估计出偏转角，从而求出目标信号在主瓣干扰下的角度估计值。

3 仿真实验与分析

为验证所提方法性能，基于Matlab进行仿真。实验中考虑12×12的平面阵，阵列划分为4×4的子阵列，阵元间距dy=dz=0.5λ，其方位、俯仰向主瓣宽度为7.6°。目标的信噪比为20 dB，干扰的干噪比为35 dB，训练样本数为120，约束间隔为(3°,3°)。假设动目标初始方向为(1°,0.5°)，3个干扰分别位于(3.5°,3°)、(2.5°,5°)和(4.5°,4°)。由于空间谱峰搜索相对于单脉冲测角而言运算量太大，对于系统实时性影响较大，所以本文仅通过如图2所示的空间谱峰搜索来确定主波束初始指向以及获得先验干扰导向矢量，而不考虑用来进行后续的动目标测角与角跟踪。

图2 空间谱峰搜索

将本文所提方法与常规自适应单脉冲方法以及多点约束自适应单脉冲方法进行对比，结果如图3～5所示。从图中可以看出，常规方法和多点约束自适应单脉冲方法受主瓣干扰影响导致和波束方向图严重畸变，而本文所提方法处理了主瓣干扰下信号导向矢量和协方差矩阵的失配问题，提高了主瓣干扰下的自适应波束形成性能。

图3 常规自适应和波束方向图

图4 多点约束自适应和波束方向图

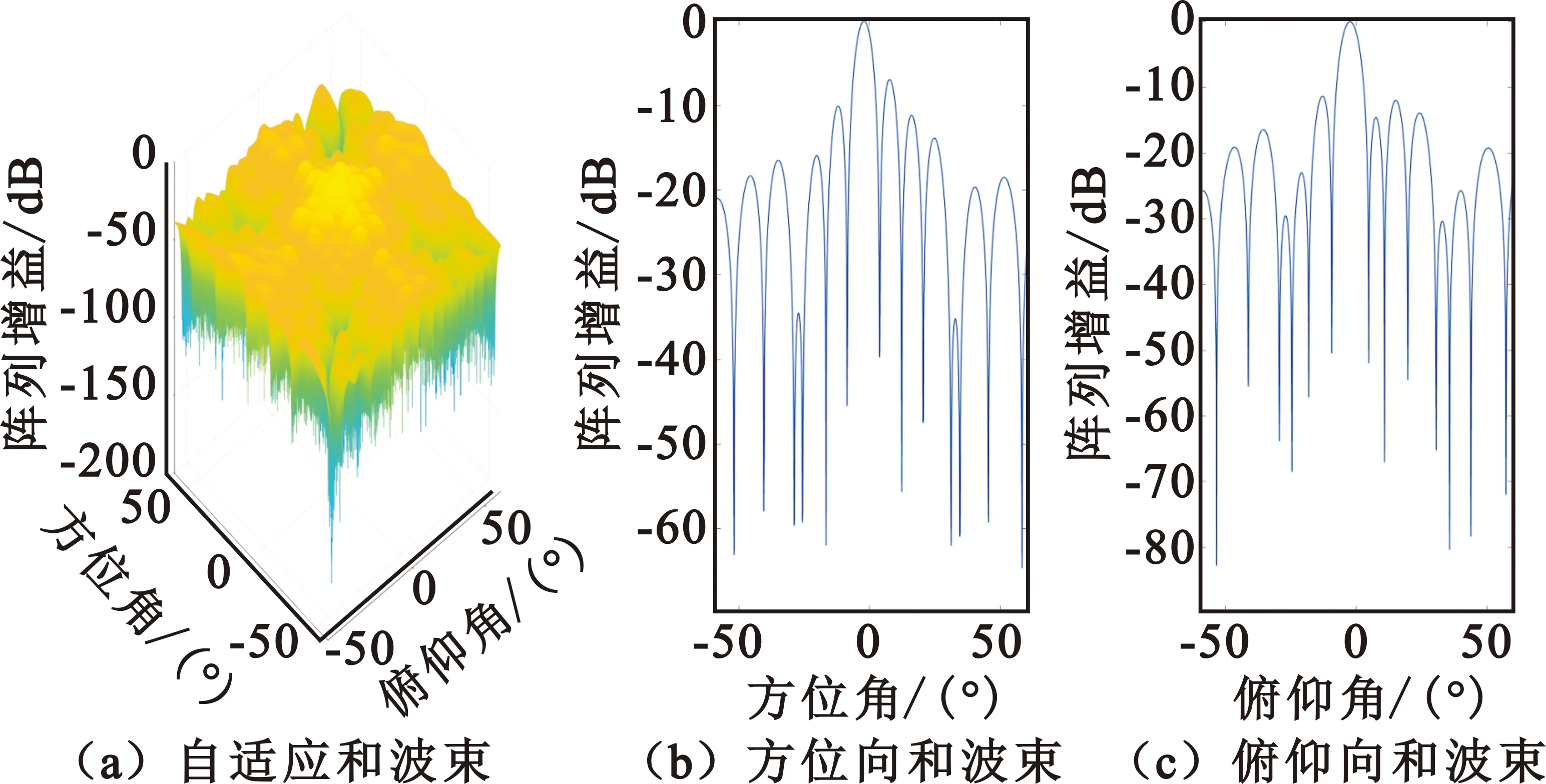
图5 稳健自适应和波束方向图

图6～8分别给出了主瓣干扰下的常规自适应单脉冲比曲面图、多点约束自适应单脉冲比曲面图与稳健自适应单脉冲比曲面图，可以看出，常规自适应单脉冲比曲面在主瓣大部分区域产生严重失真；多点约束自适应单脉冲比曲面仅在动目标当前方向(1.5°,1°)以及主瓣干扰附近产生较大失真；本文所提方法通过协方差矩阵双层重构避免了目标“自消”，同时基于联合线性约束避免了单脉冲比曲面严重失真。

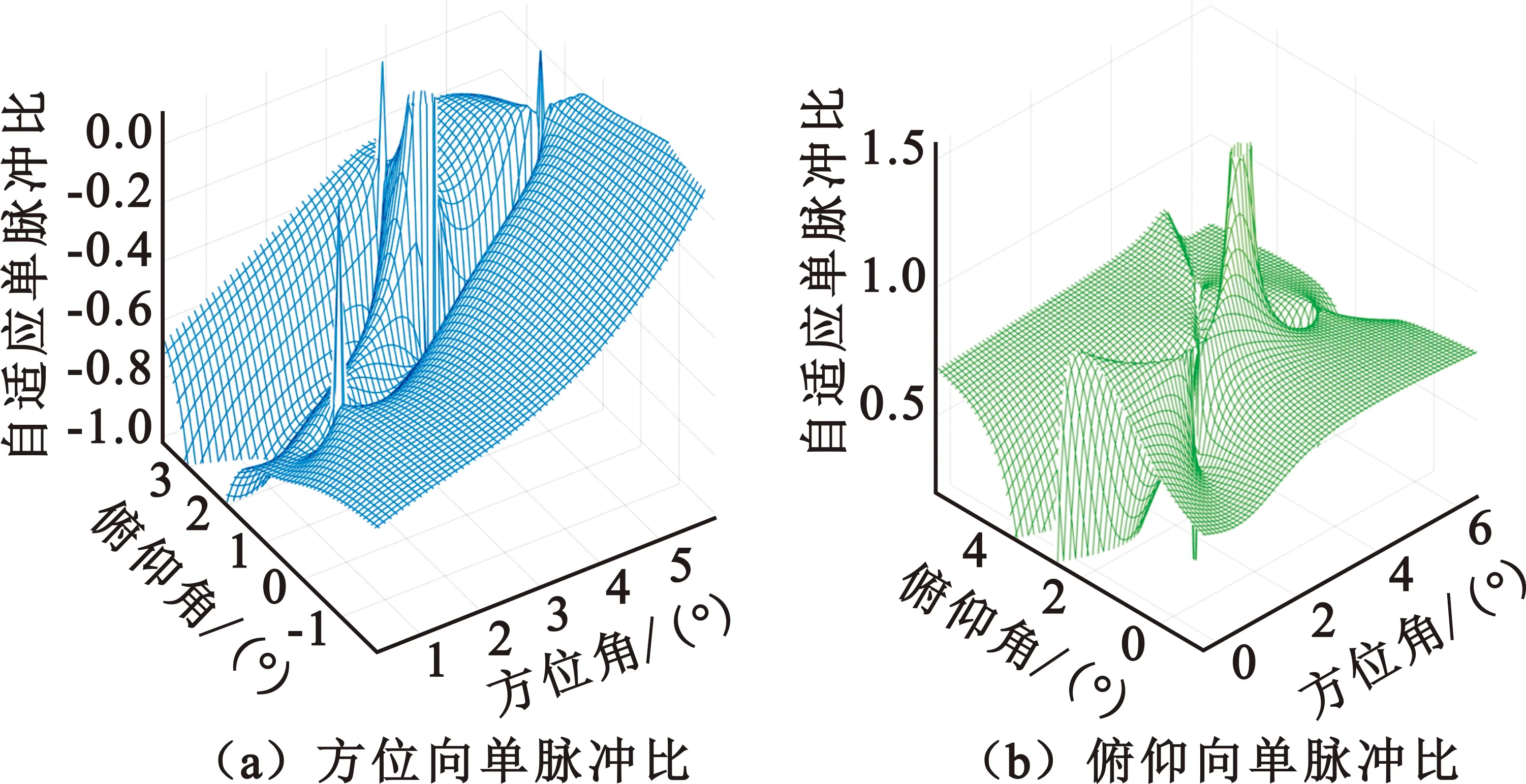
图6 常规自适应单脉冲比曲面图

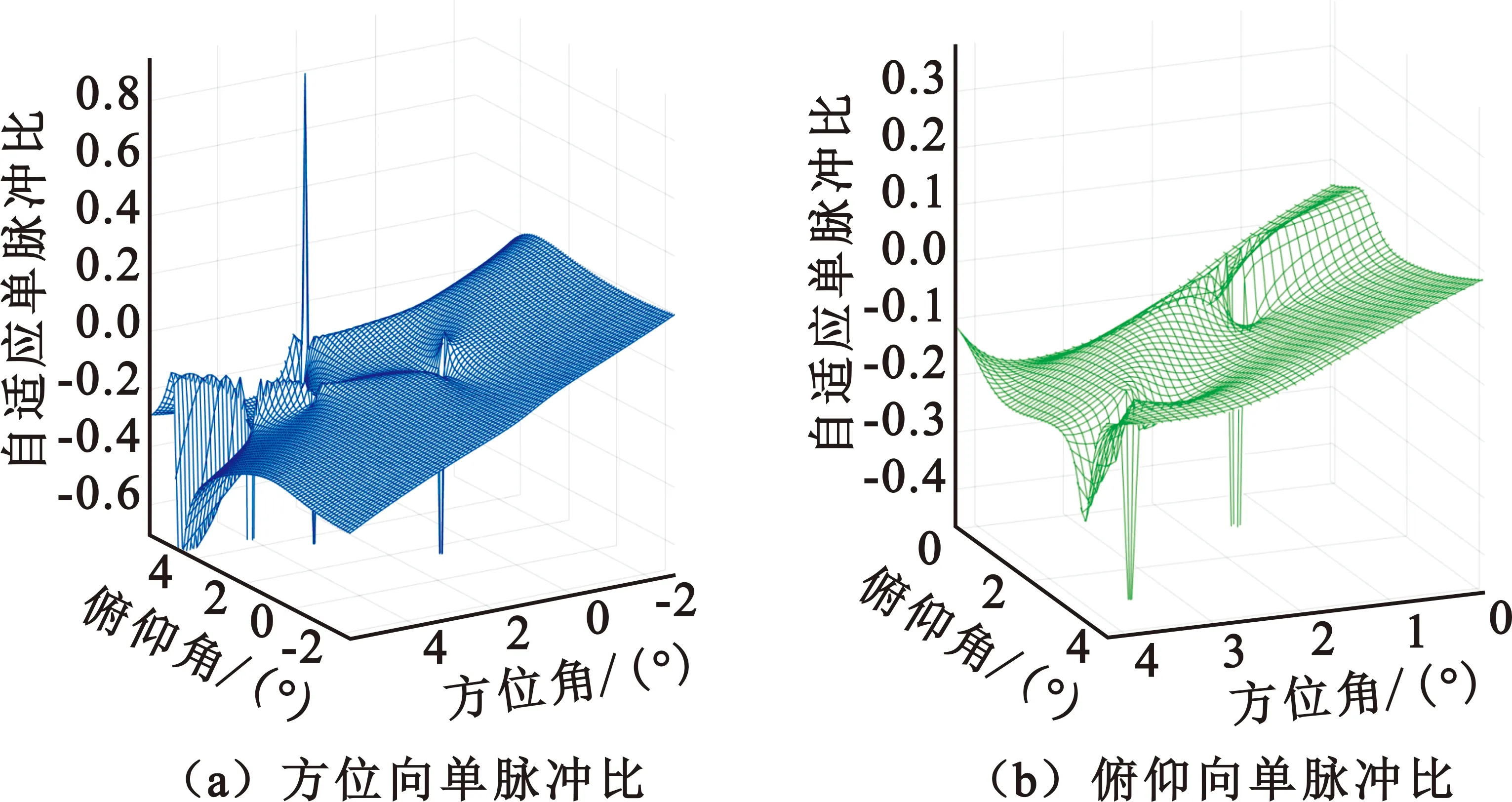
图7 多点约束自适应单脉冲比曲面图

图8 稳健自适应单脉冲比曲面图

针对上述设定进行100次仿真实验，图9给出了有无主瓣干扰的常规自适应单脉冲测角，图10和图11分别给出了主瓣干扰下的多点约束自适应单脉冲测角和稳健自适应单脉冲测角。通过实验计算得到以上三种方法在主瓣干扰下的方位角均方根误差分别为0.92°、0.49°、0.13°，俯仰角均方根误差分别为0.97°、0.51°、0.16°。可以看出，在主瓣干扰影响下，常规方法的测角性能明显下降,多点约束自适应单脉冲方法相对于常规方法而言测角误差有所减小，而本文方法相对以上两种方法而言误差更小，测角精度更高。根据上述对比可知，本文所提方法解决了自适应波束形成性能恶化的问题，避免了自适应单脉冲比曲面在主瓣干扰下严重失真，干扰抑制能力得到了进一步的提升，测角精度有了显著提高。

图9 常规自适应单脉冲测角

图10 多点约束自适应单脉冲测角

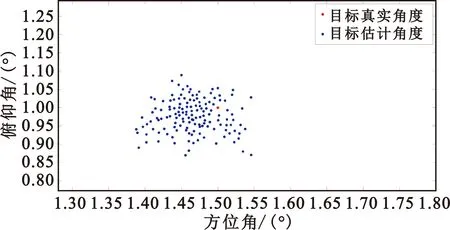
图11 稳健自适应单脉冲测角

4 结束语

本文针对常规自适应单脉冲算法在主瓣干扰的情况下使得自适应波束形成性能恶化进而导致单脉冲比特性曲线产生严重失真的问题，提出了一种基于协方差矩阵双层重构的稳健约束自适应单脉冲测角方法。该方法利用协方差矩阵双层重构来解决导向矢量与协方差矩阵失配问题，利用方位和俯仰角的联合约束来避免自适应单脉冲比发生严重失真。与常规自适应单脉冲算法相比，该方法干扰抑制能力和测角精度均有较大提升。

本文所提方法主要针对单目标进行测角跟踪，但对于该方法在主瓣干扰下进行多个动目标测向以满足多目标角跟踪性能还需要进一步研究。