基于频率计算系杆拱桥吊杆张拉力的实用公式

张戎令， 杨子江， 朱学辉， 梁庆福， 徐瑞鹏

(1. 兰州交通大学土木工程学院，甘肃 兰州730000;2. 中川铁路有限公司，甘肃 兰州730000;3. 兰州铁路局建设管理处，甘肃 兰州730070)

拱桥吊杆是结构的关键构件之一，直接承受、传递结构的荷载，由于系杆拱桥属于内部高次超静定结构，调整任意吊杆的张拉力将使结构内力重分布，改变结构的受力状态.振动测定法［1-4］是目前工程中普遍应用的测定吊杆张力的方法，该方法将索理想化为张紧的弦.由于计算式中受到复杂边界条件、垂度、抗弯刚度等的影响，造成吊杆实际受力与理论计算不一致.这些不确定因素的影响，有时会带来不可接受的误差，需要对弦公式进行修正［5］，许多学者为了精确计算索力，进行了大量的研究.孙永明［6-7］提出了考虑端部性质影响的修正索力计算公式;Zui［8］考虑吊杆弯曲刚度和垂度，建立了近似解低阶频率估算索力公式;任伟新等［9］采用能量法和曲线拟合法，分别建立了考虑索垂度和弯曲刚度的基频索力计算公式;Armin［10］给出了考虑吊杆抗弯刚度、垂度延伸特性的统一解，并提供了确定索振动方式和对应频率的方法;田广宇［11］研究了位移测量误差对基于静力位移的索力识别结果的影响;Yozo 等［12］采用渐近式分析得出了索的模态阻尼比;刘钊［13］基于能量法求解了索力计算公式;Nam 等［14］认为索的柔性减小阻尼约20%，同时增加了阻尼器的阻尼系数.以上学者从索的边界条件、抗弯刚度及垂度等方面研究了索的计算方法.但是根据吊杆的振动特性发现，以上研究均没有考虑转动惯量和剪切变形及两者耦合作用下对索力的影响;张戎令等［15］基于结构振动理论，建立了吊杆索力计算公式，考虑了转动惯量和剪切变形耦合影响.实际吊杆是由高强钢绞丝和PE(polyethylene)护套两种材料组成，实际频率为两者的耦合频率;吊杆的边界条件在不同结构中差异较大;吊杆有效长度在实际中亦难以确定.在实际索力计算中需要一种综合考虑以上影响的有效方法.

本文根据已有研究成果及吊杆的动力特性，结合抗弯刚度的影响，同时考虑转动惯量和剪切变形的影响及其耦合作用，推导了吊杆铰接下索力计算公式;在索力计算式中，频率受到索结构自身和外界因素的影响较多，其对索力计算值影响较大;根据实测频率对索力灵敏度进行分析，给出了索力计算的实用公式.

1 吊杆受力分析及求解

吊杆是由等直径的钢绞丝制成，假设其为等截面，则截面面积S 和抗弯刚度EI 均为常量;在振动中，横向发生位移，同时与吊杆中心线相切的线段产生一个剪切角γ. 在张拉力作用下，吊杆横向位移为u(x，t)是随坐标轴x 和时间t 连续变化的函数.取吊杆上一微段dx 为隔离体，吊杆受力见图1，图中，f1为第一阶频率. 如图1 所示，微段吊杆在运动过程中处于动平衡状态，由水平力及力矩平衡条件可得

式中:Q 为剪力;m 为吊杆的线密度;M 为弯矩;T 为拉力;ρ 为材料的质量密度;I 为截面惯性矩;θ 为截面转角.

根据吊杆弯曲理论，剪力Q 与剪切角γ 的关系式为

式中:Sc为截面有效剪切系数;G 为剪切模量.

由图1 可知，截面转角θ 和剪切角γ 的关系为

由式(1)～(3)可得

图1 吊杆微段隔离体受力图Fig.1 Force diagram of the micro-element of suspender

根据吊杆结构的弯曲理论，弯矩M 与曲率∂θ/∂x 的关系为

将式(2)、(5)代入式(1)，并对x 求导，可得

将式(4)代入式(6)整理可得

为简化分析，假设位移函数随时间简谐变化，令

式中:Y(x)为吊杆振动形状，不随时间变化;ω 为吊杆振动频率.

式(8)代入式(7)，并令

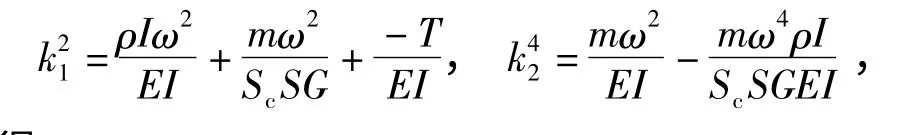
可得

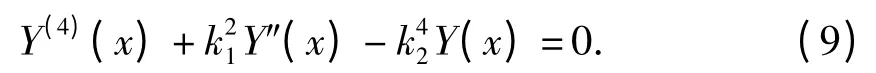
设解的形式为Y(X)=Aeβx，将其代入式(9)，得

令

因此，式(10)的解为

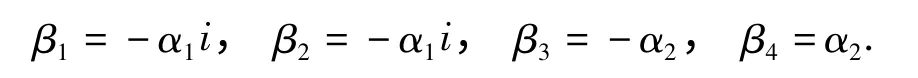
将β1～β4代入Y(X)=Aeβx，用双曲函数和三角函数替换指数函数，得

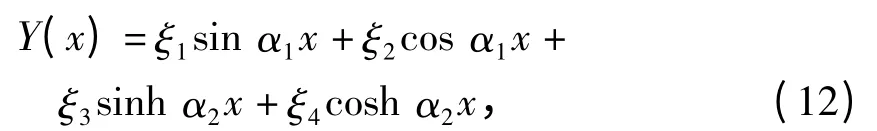
式中:ξ1、ξ2、ξ3、ξ4为吊杆的振动形状.

根据吊杆的受力情况，假设两端为铰接，杆长为l，则边界条件为

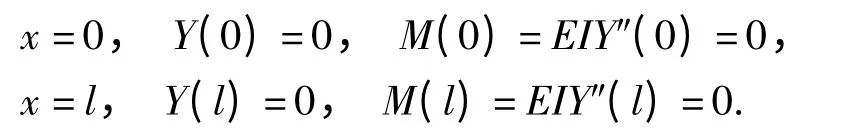
根据边界条件可解得:

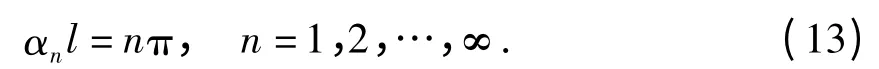
将α1、α2代入式(11)，通过中各参数的关系，可求出吊杆两端铰接情况下索力的计算式为

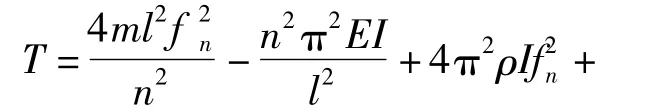
式中:fn为第n 阶频率.

式(14)中第1 项为经典弦振动基本方程;第2项考虑抗弯刚度的影响;第3 项考虑转动惯量的影响;第4 项考虑剪切变形的影响;第5 项为吊杆转动惯量和剪切变形二者耦合影响.

在不考虑转动惯量和剪切变形的影响时，式(14)变为

在不考虑转动惯量和剪切变形和抗弯刚度时，式(14)变为

文中推导的式(14)虽在理论上完善了吊杆张拉力的计算公式，但一方面由于考虑转动惯量和剪切变形的索力公式是基于梁理论进行分析的，实际中的索不完全等同于梁，剪切变形和转动惯量对高频会有些影响;另一方面公式中涉及到剪切系数、抗弯刚度等参数，在实际结构中难以准确计算，即使通过实际索力将剪切变形、转动惯量及其耦合项进行简化、拟合后，计算式中参数较多，依然较难准确计算出与实际符合的索力.因此，结合吊杆长度，基于实际频率与索力的关系，通过频率的灵敏度分析，修正本文推导的公式，进而得到计算吊杆张力的实用公式.

2 频率灵敏度分析

2.1 试验概况

以实际工程1 ～128 m 系杆拱桥为研究对象，其吊杆采用PESC7-085 丝φ 7 mm 的低松弛环氧喷涂高强钢丝成品吊杆，标准强度为1 670 MPa，弹性模量为195 GPa，截面面积为3 271 mm2，吊杆直径为71.2 mm，单位长度质量为25.7 kg/m，抗弯刚度为246.1 kN·m2.拱桥吊杆布置及编号见图2.

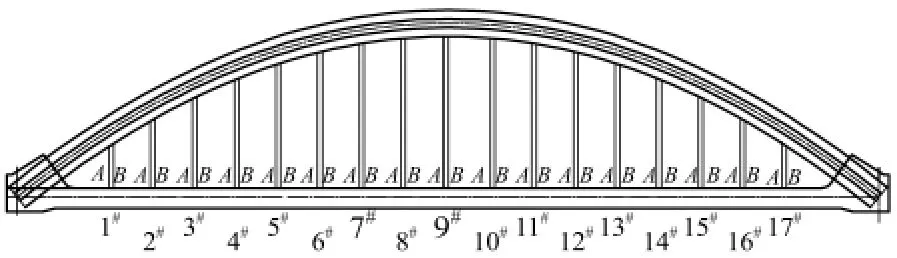
图2 吊杆编号及布置形式Fig.2 Suspender number and arrangement

每一对吊杆有两根吊杆，分别记为A、B. 实际吊杆顶端并非穿过拱肋，而是固定在下弦管下缘，并安装有球形支座，其简化成铰接更为合理.

2.2 数据分析

现场采用频率法进行索力测试，由于实际吊杆共68 根，数量较多，因此选取典型吊杆进行分析，分别选1#吊杆(17#吊杆)、5#吊杆(13#吊杆)、9#吊杆，即选取拱桥最短、中间、最长吊杆为研究对象，分析吊杆频差与阶数的关系.吊杆各阶频率变化情况见图3，图中，f1为一阶频率，Hz.

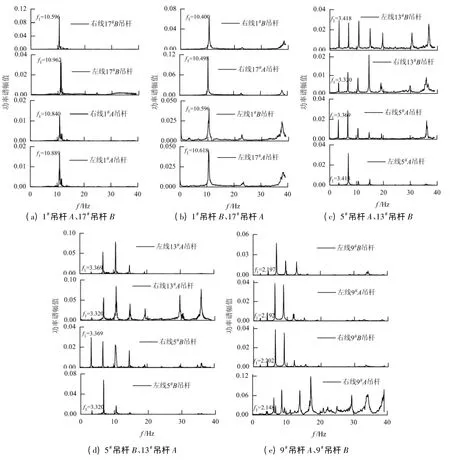
图3 不同吊杆频谱图Fig.3 Frequency spectra of different suspenders

由图3 可以看出，虽然吊杆约束形式相同、材料相同、长度相同，但对应的同阶频率相差较大.有些吊杆只有3 ～8 阶频率，甚至只有1 阶频率(如1#吊杆A 和17#吊杆B 所示)，即使有高阶频率(如右线9#吊杆A)，按照频率识别法，在平均谱图中找出从大到小排列的10 阶峰值:①用其它值除以最小值，若结果大部分为整数，则最小值即为基频，若结果大部分约为0.5 的整数倍，则用最小值减去频差就是基频;②对10 个峰值求最大公约数，这个最大公约数就是基频.以上方法很难精确得出反应实际索力的基频. 由于实际吊杆在转动惯量、剪切变形、吊杆有效长度、钢绞线和PE 护套耦合频率等因素影响下，导致实测索力频率随着阶数的提高，频差越大.以图3 中右线9#A 吊杆为例，1 阶频率为2.148 0 Hz，10 阶频率对应求出的基频为2.504 9 Hz，13 阶 频 率 对 应 求 出 的 基 频 为3.005 0 Hz.可见高阶频差作为基频误差很大.

为了确定出精确的索力，分析了各阶频率差与阶数的拟合曲线见图4. 由图4 可以看出，不同吊杆、不同阶频率差拟合有线性和非线性曲线，非线性曲线又有二次、三次曲线的不确定性. 同时由于现场索力测试传感器通常布置在距吊杆下端3.5 m 处(以本桥为例)，这样通过频率法测得的频率以高阶频率为主，因此，直接通过高阶频率差求基频会造成基频值识别变大，从而导致索力识别值偏大.

图4 索力频率差拟合Fig.4 Frequency difference fitting of cable force

通过以上不同吊杆频率和频率差分析，本文通过各吊杆一阶频率的分析，根据实际张拉力反推部分吊杆的理论频率，将实际张拉测得的频率与理论频率进行拟合，进而得到频率的修正值，推导出适用的索力计算简化公式.

为了修正频率，同时保证修正后频率的精度满足要求，通过1#～9#吊杆的拟合，将所有吊杆统一成一条曲线后，难以保证修正后的精度. 通过各个实测吊杆的频率分布特点，按照不同吊杆长度，将吊杆分成3 个长度范围，分别进行拟合分析. 具体分析见图5、图6.

通过1#～9#吊杆(9#吊杆仅统计A)实测频率和理论频率的曲线拟合分析，得到索力计算实用的公式为

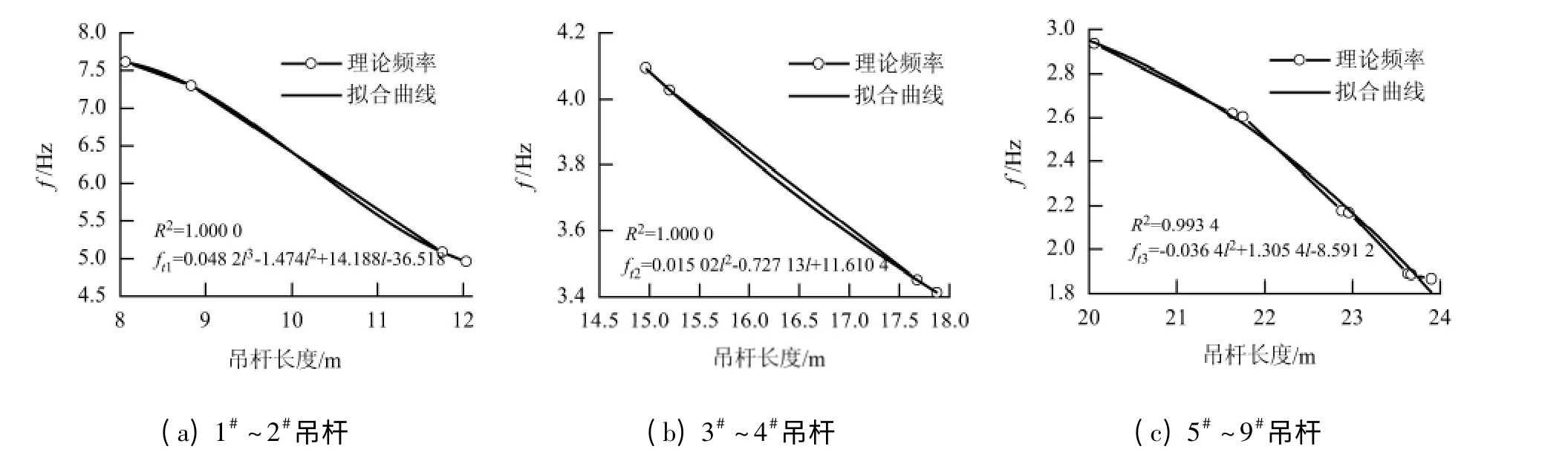
图5 1# ～9#吊杆理论频率与吊杆长度拟合关系Fig.5 Fitted relationship between theoretic frequency and suspender length for 1# ～9# suspenders

式中:ki=fti/fai，这里，fti为i 值时吊杆的理论频率，fai为i 值时吊杆的实测频率，i 根据吊杆长度分别取1，2，3.

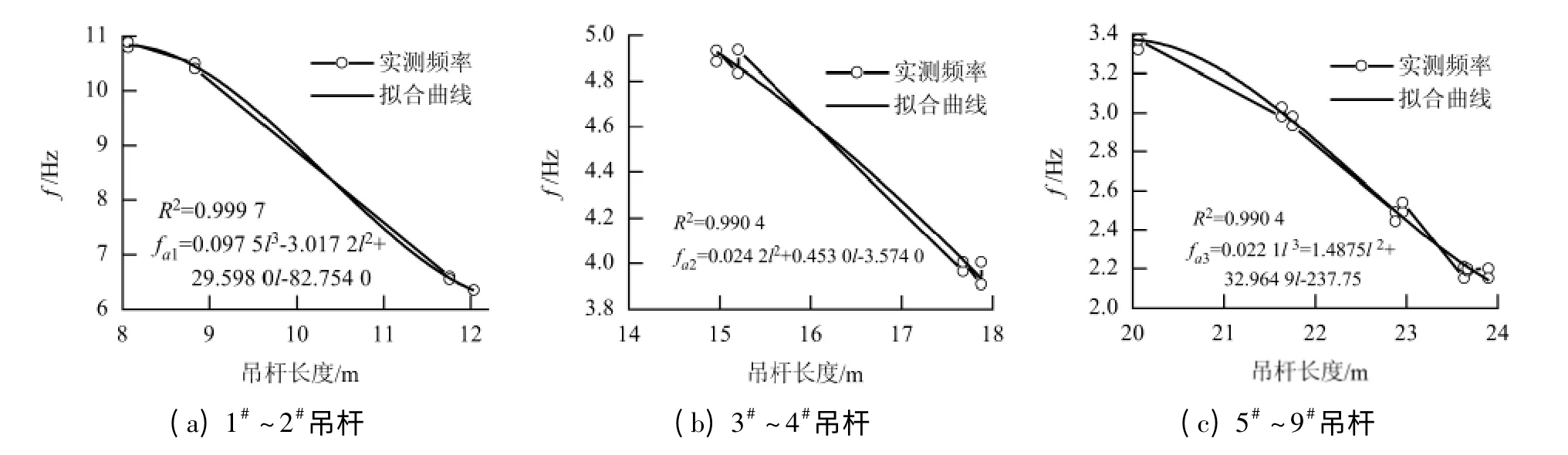
图6 1# ～9#吊杆实测频率与吊杆长度拟合关系曲线Fig.6 Fitted relationship between measured frequency and suspender length for 1# ～9# suspenders

3 算例分析

为了验证式(17)与实际的吻合性，将本座桥梁剩余的未分析吊杆(9#吊杆B ～17#吊杆AB)做为研究对象，进行理论计算张拉力与实际张拉力对比分析.计算参数取值(见2.1 试验概况)均以实际系杆拱桥进行取值. 具体分析结果详见表1，表中基频为第一阶固有频率.

表1 张拉索力计算比较Tab.1 Suspender tension comparison

由表1 可看出:修正前式(14)最大误差为-5.2%，尽管修正前式(14)有个别索力误差比式(17)误差小，但式(14)平均误差为0.8%;实用式(17)在式(14)的基础上大大的简化了计算，而且计算出的索力与实际索力吻合较好，理论计算最大误差为4.7%，平均误差仅为0.3%，误差均控制5.0%以内，修正后索力整体误差更小，索力受力更均匀，可以满足实际索力张拉控制要求. 考虑到实际吊杆边界的复杂性和吊杆振动特性，特别是对短吊杆和下端张拉的拱桥吊杆，为了减少边界条件的影响，建议将索力传感器尽量布置在索的中间位置或尽量远离张拉端的位置，以减小固定端的影响，准确测得索的实际振动频率，保证索力计算的准确性.

4 结 论

本文通过吊杆振动力学理论分析并结合实测试验，验证了系杆拱桥吊杆索力计算简化分析方法的有效性，得出以下结论:

(1)弦振动理论公式及考虑抗弯刚度公式是本文的特例，即本文公式在不考虑转动惯量和剪切变形影响时，可得仅考虑抗弯刚度的索力计算公式;同时不考虑抗弯刚度时，可得经典的弦振动理论公式;

(2)本文吊杆索力计算实用公式误差可以控制在5%以内，能够保证索力控制的精度要求. 计算中直接应用一阶频率进行计算，公式计算简单方便.

致谢:兰州交通大学青年科技基金项目资助(2012028).

［1］ RUSSELL J C，LARDNER T J. Experimental determination of frequencies and tension for elastic cables［J］. Journal of Engineering Mechanics，ASCE，1998，24(10):1067-1072.

［2］ KIM B H，PARK T. Estimation of cable tension force suing the frequency-based system identification method［J］. Journal of sound and Vibration，2007，304(3/4/5):660-676.

［3］ CEBALLOS M A，PRATO C A. Determination of the axial force on stay cables accounting for their bending stiffness［J］. Journal of sound and Vibrationg，2008，317(1/2):127-141.

［4］ MA Haitao. Exact solutions of axial vibration problems of elastic bars［J］. International Journal for Numerical Methods in Engineering，2008，75(2):241-252.

［5］ MEHRABI A B，TABATABAI H. A unified finite difference formulation for free vibration of cables［J］.Journal of Structural Engineering， ASCE， 1998，124(11):1313-1322.

［6］ 孙永明，李惠. 端部性质对频率法测量竖直拉索索力影响分析［J］. 工程力学，2013，30(8):10-17.SUN Yongming，LI Hui. Effect of extreme properties of vertical cable on the cable force measurement by frequency-based method［J］. Engineering Mechanics，2013，30(8):10-17.

［7］ 孙永明，孙航，任远. 频率法计算匀质竖直拉索索力的实用公式［J］. 工程力学，2013，30(4):211-218.SUN Yongming，SUN Hang，REN Yuan. Practical formulas to calculate tensions of vertical cable with uniform properties by frequency method［J］.Engineering Mechanics，2013，30(4):211-218.

［8］ ZUI H，SHINKE T，NAMITA Y. Practical formulas for estimation of cable tension by vibration method［J］.Journal of Structural Engineering， ASCE， 1996，122(6):651-656.

［9］ 任伟新，陈刚. 由基频计算拉索拉力的适用公式［J］. 土木工程学报，2005，38(11):26-31.REN Weixin，CHEN Gang. Practical formulas to determine cable tension by using cable fundamental frequency［J］. China Civil Engineering Journal，2005，38(11):26-31.

［10］ ARMIN B， HABIB T. Unified finite difference formulation for free vibration of cables［J］. Journal of Structural Engineering，124，11:1313-1322.

［11］ 田广宇，郭彦林，张博浩，等. 车辐式屋盖结构的一种索力识别方法的误差研究［J］. 工程力学，2013，30(3):126-132.TIAN Guangyu，GUO Yanlin，ZHANG Bohao，et al.Research on error of a cable force estimation methodfor spoke structural roofs［J］. Engineering Mechanics，2013，30(3):126-132.

［12］ YOZO Fujino. Design formulas for damping of a stay cable with a damper［J］. Journal of Structural Engineering，2008，134(2):269-278.

［13］ 刘钊. 基于能量法的系杆拱桥最优吊杆内力的确定［J］. 工程力学，2009(8):168-173.LIU Zhao. Determination of the optimal hanger forces for tied-archbridges based on energy methods［J］.Engineering Mechanics，2009(8):168-173.

［14］ NAM Hoang，YOZO Fujino. Analytical study on bending effects in a stay cable with a damper［J］.Journal of Engineering Mechanics，2007，133，11:1241-1246.

［15］ 张戎令，王起才，马丽娜，等. 考虑转动惯量和剪切变形耦合的铰接吊杆索力实用计算公式［J］. 中国铁道科学，2014，35(5):30-37.ZHANG Rongling，WANG Qicai，MA Lina，et al.Practical formulas for cable force of hinged suspender considering the coupling effects of moment of inertia and shearing deformation［J］. China Railway Science，2014，35(5):30-37.