剩余类环Z/(pn)上若干类单圈多项式构造
2012-07-25戚文峰
游 伟 戚文峰
(解放军信息工程大学 郑州 450002)
1 引言
若f(x)是一个整系数多项式,当x通过模m的一个完全剩余系时,f(x)也通过模m的一个完全剩余系,则称f(x)是模m的一个置换多项式。关于置换多项式的研究结果非常多,可参考文献[1-7]。引起置换多项式迅速发展的一个主要原因是它已逐渐在数论,组合论,密码系统等领域中得到应用。事实上,著名公钥密码体制 RSA[8]和分组密码算法 RC6[9]就是其中的两个应用。
本文研究的是一类特殊的置换多项式,即剩余类环上的单圈多项式(见定义 1)。单圈多项式在密码学的众多领域都有重要应用。例如,在伪随机数发生器[10]的理论中,状态转移函数必须提供伪随机性,特别地,它必须保证状态序列的元素分布和周期。为了达到这个目的,我们可以选择单圈多项式作为状态转移函数,这样就可以保证状态序列达到最大周期并且其元素满足严格一致分布。事实上,经典的线性同余发生器使用的即是一次单圈多项式,它的优势是实现速度快,但弱点是结构过于简单。本文的目标是构造任意次数的单圈多项式,这样就可以利用高次单圈多项式来产生非线性同余发生器以取代线性同余发生器。伪随机数在包括仿真,抽样,数值分析,公钥密码算法设计等众多领域中都有着不同形式的应用。另外,单圈多项式还可以用来构造拉丁方。拉丁方的应用也是极其广泛的。例如,在保密通信网络中用来做口令的分发;以及在某些密码算法的设计中作为多重置换来使用。
Knuth[11]给出了剩余类环Z/(m)上的所有一次和二次单圈多项式的构造。Larin[12]和 Durand等[13]则分别给出了Z/(2n)和Z/(3n)上任意次单圈多项式的全部构造。然而,对于一般的素数p,关于Z/(pn)上单圈多项式的构造目前还没有任何结果。其实,这也并不奇怪,因为即使是有限域Z/(p)上置换多项式的构造都是极其有限的。
本文通过刻画多项式的系数给出了Z/(pn)(p≥5)上若干类单圈多项式的构造。由于Z/(pn)上单圈多项式的构造可以归结到Z/(p2)上,本文首先通过刻画系数满足的条件给出了Z/(5)上任意次单圈多项式的构造,并在其基础上给出了Z/(52)上 6 次单圈多项式的全部构造。另外,本文还给出了Z/(p2)上 (p-1) 次单圈多项式的部分构造。
2 基础知识
定义1[12]设f(x)∈Z[x],m≥ 2 是正整数,若递归序列ui+1=f(ui)(modm) 的周期达到m,则称f(x)为剩余类环Z/(m)上的单圈多项式。
引理1[12]设n≥2,若多项式f(x)∈Z[x]在Z/(pn)上是单圈,则f(x)在Z/(pn-1)上也是单圈。
引理2[12]设p为素数,若多项式f(x)∈Z[x]在Z/(p3)上是单圈,则对任意正整数n,f(x)在Z/(pn)上都是单圈;特别地,当p∉{2, 3}时,若多项式f(x)∈Z[x]在Z/(p2)上是单圈,则对任意正整数n,f(x)在Z/(pn)上都是单圈。
注 1:由引理 1 和引理 2 可知,当p≥5 时,f(x)在Z/(pn)(n≥2) 上是单圈当且仅当f(x)在Z/(p2)上是单圈。因此,当p≥5时,对Z/(pn)(n≥2) 上单圈多项式的研究都可以归结到Z/(p2) 上。

下面的引理刻画了Z/(p)与Z/(p2)上的单圈多项式所满足条件之间的联系。
引理3[13]多项式f(x)∈Z[x],若f(x)在Z/(p)上是单圈,则下面的3个条件是等价的。(1)f(x) 在Z/(p2)上是单圈;(2)对任意x∈Z,fp(x)-x≠0(modp2),并且 (fp)'(x)≡1(modp); (3)存在x∈Z,满足fp(x)-x≠0(modp2),并且 (fp)'(x)≡1(modp)。
注2:由引理 3 可知,若f(x)在Z/(p)上是单圈,则f(x)在Z/(p2)上也是单圈 ⇔fp(0) ≠ 0(modp2),并且 (f p)′(0)≡ 1(modp)。
3 Z/(5)上单圈多项式的系数刻画
3.1 常数项为 1 的情形
定理1设f(x)=adxd+ad-1xd-1+…+a1x+1∈Z[x],则f(x)在Z/(5)上是单圈当且仅当A0,A1,A2,A3满足表1中条件之一。
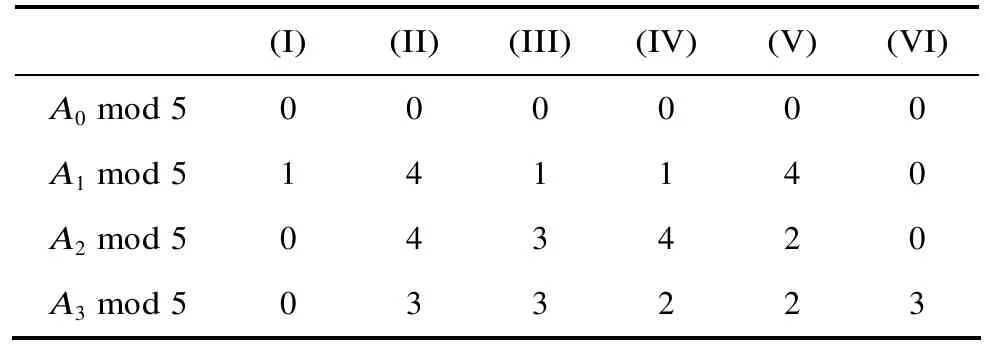
表1 f(x)在Z/(5)上是单圈的条件
证明因为f(x)=adxd+ad-1xd-1+…+a1x+1,所以
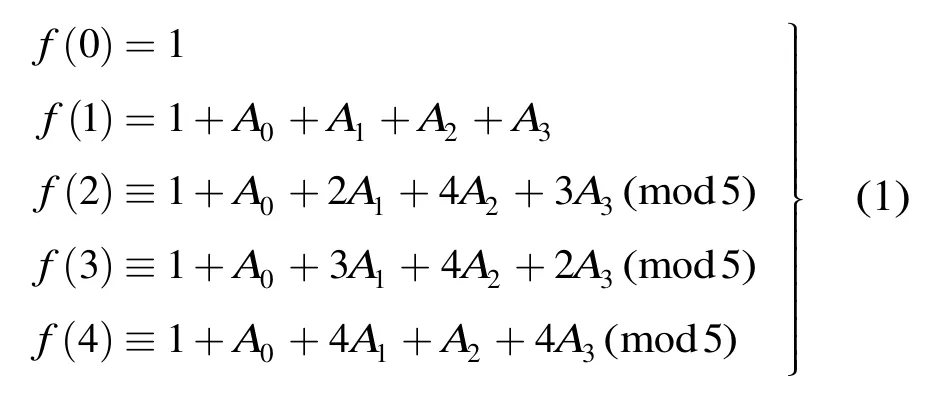
若f(x)在Z/(5)上要构成单圈,则f(1)=1+A0+A1+A2+A3≠ 0 或 1(mod 5),从而有A0+A1+A2+A3≡1, 2或3 (mod 5)。下面分情形讨论:
(1)当A0+A1+A2+A3≡ 1(mod5),此时,f(x)在Z/(5)上是单圈当且仅当

连同f(0)=1和f(1)≡2(mod 5),分别求解上述两个同余方程组可得(A0,A1,A2,A3)≡(0,1,0,0)或(0,4,4,3)·(mod 5)。
(2)当A0+A1+A2+A3≡2(mod 5),同理得f(x)在Z/(5)上是单圈当且仅当(A0,A1,A2,A3)≡(0,1,3,3)或(0,1,4,2)(mod 5)。
(3)当A0+A1+A2+A3≡3(mod 5),同理得f(x)在Z/(5)上是单圈当且仅当(A0,A1,A2,A3)≡(0,4,2,2)或(0,0,0,3) (mod 5)。 证毕
3.2 常数项不为 1 的情形
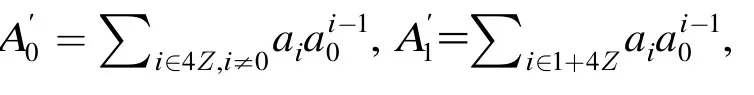


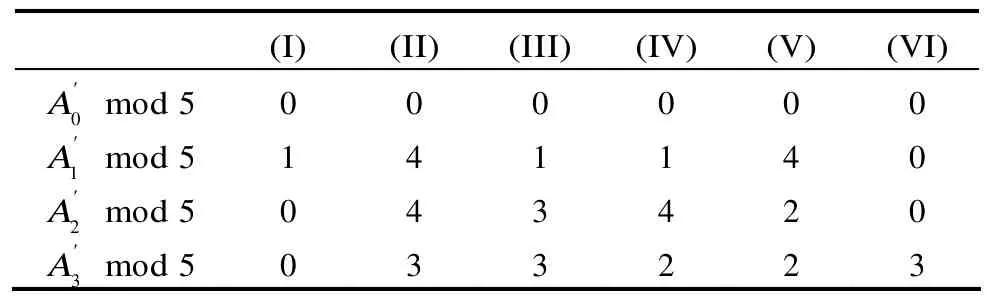
表2 g(x)在Z/(5)上是单圈的条件
4 Z/(52)上 6 次单圈多项式的全部构造
4.1 常数项为 1 的情形
引理4若f(x)在Z/(5)上是单圈,则(f5)′(0)≡a1[(D1+D3)2-(D0+D2)2][(D1-D3)2-(2D2+3D0)2](mod 5)。
证明 因为fk(x)=f(fk-1(x)),所以 (fk)′(x)=f′(fk-1(x))·(fk-1)′(x),故有(f5)′(x)=f′(f4(x))·(f4)′·(x) = … =f′(f4(x)) ·f′(f3(x)) ·f′(f2(x)) ·f′(f(x))·f′(x)。又f(x)在Z/(5)上是单圈,从而对任意x∈Z,有(f5)′(x)≡f′(0)f′(1)f′(2)f′(3)f′(4)(mod 5)。另外
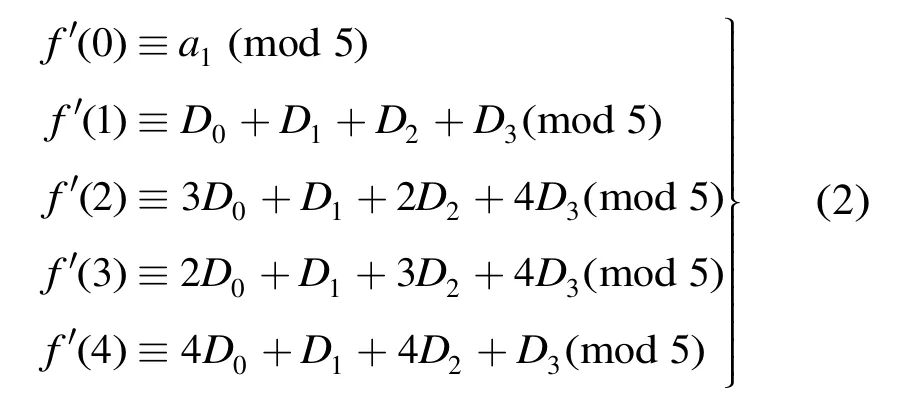
因此(f5)′(0)≡a1[(D1+D3)2-(D0+D2)2][(D1-D3)2-(2D2+3D0)2](mod 5)。 证毕
引理5f(x)如上,对任意素数p和正整数k,若fk(0)≡c(modp), 0 ≤c≤p-1,则fk+1(0)≡f(c)+f'(c)(fk(0)-c)(modp2)。
证明 因为fk(0)≡c(modp), 0 ≤c≤p-1,所以fk(0)-c≡0(modp)。则有
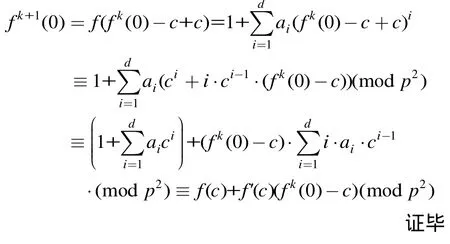
注 3:若(A0,A1,A2,A3)≡(0,1,0,0)(mod 5),则由式(1)可知f(0)=1,f2(0)≡2(mod 5),f3(0)≡3·(mod 5),f4(0)≡-1 (mod 5)。
由引理5通过迭代可得

定理2设f(x) =a6x6+a5x5+a4x4+a3x3+a2x2+a1x+1∈Z[x],则f(x)在Z/(52)上是单圈当且仅当a1≡1(mod 5),a2≡a3≡a5≡a6≡0 (mod 5),a4≡0·(mod 5)且a4≠ 5(mod 52)。
证明 由定理 1 及注 2 可知,若f(x)在Z/(5)上是单圈,即A0,A1,A2,A3满足表1中条件(I)-条件(VI)中的某一个,则f(x)在Z/(52)上是单圈当且仅当 (f5)′(0)≡1(mod 5),及f5(0)≠0(mod 52)。
由Ai和Di的定义易得
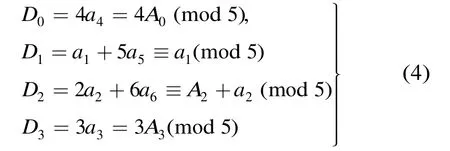
下面分情况进行讨论:
(1)当 (A0,A1,A2,A3)≡(0,1,0,0)(mod 5),由式(4)可得D0≡0(mod 5),D1≡a1(mod 5),D2≡a2(mod 5),D3≡0(mod 5)。

由此可知,为了给出f(x)在Z/(52)上是单圈的充要条件,我们只需说明当条件式(5)满足时,f5(0) ≠ 0·(mod 52) 当且仅当a4≠ 5(mod 52)。
当条件式(5)满足时,由式(2)和式(4)可得f′(2)≡a1+2a2≡1(mod 5),f'(3)≡a1+3a2≡1(mod 5),f'( 4 )≡a1+4a2≡1(mod 5)。
另外,由式(3)可得
f5(0)≡f(-1)+f'(4)(f(3)+1)+f'(4)f'(3)(f(2)-3)+f'( 4 )f'(3)f'(2)(f(1)-2)(mod 52)≡f(-1)+(f(3)+1)+(f(2)-3)+(f(1)-2)(mod 52)≡5a1+15a2+10a3+24a4+20a6(mod 52)≡5-a4(mod 52)
因此,当条件式 (5) 满足时,f5(0)≠0(mod 52) 当且仅当a4≠5(mod 52)。故在此情形下f(x)在Z/(52)上是单圈当且仅当a1≡1(mod 5),a2≡a3≡a5≡a6≡0 (mod 5),a4≡0 (mod 5)且a4≠ 5(mod 52)。
(2)当(A0,A1,A2,A3)≡(0,4,4,3) (mod 5),由式(4)可得D0≡0 (mod 5),D1≡a1(mod 5),D2≡a2-1·(mod 5),D3≡ -1(mod 5)。
由引理 4 可知(f5)′(0)≡a1[(a1-1)2-(a2- 1)2][(a1+ 1)2+(a2-1)2](mod 5)。
(3)当(A0,A1,A2,A3)≡(0,1,3,3)(mod 5),同理得(f5)′(0)≡a1[(a1- 1)2- (a2- 2)2][(a1+ 1)2+ (a2- 2)2]·(mod 5)。
(4)当(A0,A1,A2,A3)≡(0,1,4,2) (mod 5),同理得(f5)′(0)≡a1[(a1+ 1)2-(a2- 1)2][(a1-1)2+(a2- 1)2]·(mod 5)。
(5)当(A0,A1,A2,A3)≡(0,4,2,2) (mod 5),同理得(f5)′(0)≡a1[(a1+ 1)2-(a2+ 2)2][(a1-1)2+(a2+2)2]·(mod 5)。

在情况(2)- 情况(6)中,遍历a1和a2的所有取值,易知 (f5)′(0) ≠ 1(mod 5)。这意味着在这些情况下f(x)在Z/(52)上都不可能构成单圈。 证毕
4.2 常数项不为 1 的情形
推论2设g(x)=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0∈Z[x],则g(x)在Z/(52)上是单圈当且仅当a1≡1(mod 5),a2≡a3≡a4≡a5≡a6≡0(mod 5),a0≠0(mod 5)且a0≠(a4/5)(mod 5)。
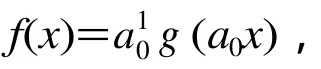
5 Z/(p2)上(p-1)次单圈多项式的部分构造
引理6设素数p>3,则

证明因为有限域Z/(p)中的所有非零元素构成乘法循环群,设=〈g〉。所以



当k= (p-1)/2 时,由欧拉定理可知
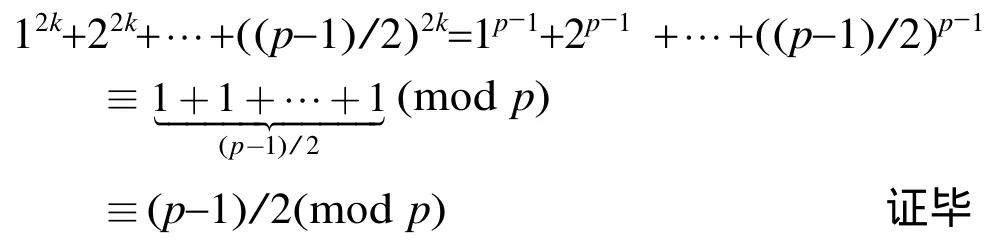
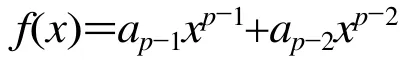
证明首先,因为a1≡1 (modp),a2≡a3≡…≡ap-2≡ap-1≡0 (modp),所以f(x)≡x+1(modp)。显然f(x)在Z/(p)上是单圈。另外,f′(x)=(p-1)ap-1xp-2+ (p-2)ap-2xp-3+…+ 2a2x+a1,因此可得f′(x)≡a1≡1(modp)。
其次,因为f(x)在Z/(p)上是单圈,类似引理4的证明可得(fp)'( 0 )≡f'( 0 )f'( 1 )f'( 2 )…f'(p-1)(modp)≡1(modp)。
最后,因为f(x)≡x+1(modp),由引理5可得

由引理 6和a1≡1(modp),a2≡a3≡…≡ap-2≡ap-1≡0(modp),有f p(0)≡2ap-1(p-1)/2+p(modp2)≡p-ap-1≠0 (modp2)。由注 2 可知,f(x)在Z/(p2)上是单圈。 证毕
6 结束语
目前,只有p=2,3 时,针对剩余类环Z/(pn)上单圈多项式的研究才全部得以解决。本文对Z/(5)上的任意次单圈多项式进行了完整的系数刻画,进一步,对Z/(52)上的 6 次单圈多项式进行了完整的系数刻画;另外,本文给出了Z/(p2)(p>3)上的(p-1)次单圈多项式的部分构造。我们下一步的工作有两个方向:第一,对Z/(p)(p>5)上的单圈多项式进行完整的系数刻画;第二,对Z/(p2)(p>3)上的任意次单圈多项式进行完整的系数刻画。
[1]Rivest R L. Permutation polynomials modulo 2w.Finite Fields and Their Applications, 2001, 7(2): 287-292.
[2]Weng Guo-biao and Dong Chao-ping. A note on permutation polynomials overZ/nZ.IEEE Transactions on Information Theory, 2008, 54(9): 4388-4390.
[3]Coulter R, Henderson M, and Matthews R. A note on constructing permutation polynomials.Finite Fields and Their Applications, 2009, 15(5): 553-557.
[4]Ostafe A. Multivariate permutation polynomial systems and nonlinear pseudorandom number generators.Finite Fields and Their Applications, 2010, 16(3): 144-154.
[5]Li Ji-you, Chandler D B, and Xiang Qing. Permutation polynomials of degree 6 or 7 over finite fields of characteristic 2.Finite Fields and Their Applications, 2010, 16(6): 406-419.
[6]Akbary A, Ghioca D, and Wang Qiang. On constructing permutations of finite fields.Finite Fields and Their Applications, 2011, 17(1): 51-67.
[7]Marcos J E. Specific permutation polynomials over finite fields.Finite Fields and Their Applications, 2011, 17(2):105-112.
[8]Rivest R L, Shamir A, and Adleman L M. A method for obtaining digital signatures and public-key cryptosystems.Communications of the ACM, 1978, 21(2): 120-126.
[9]Rivest R L, Robshaw M J B, Sidney R,et al.. The RC6 block cipher. http://theory.lcs.mit.edu/~rivest/rc6.pdf, 1998.
[10]Anashin V and Khrennikov A. De Gruyter Expositions in Mathematics. Berlin: Walter de Gruyter, 2009, Vol.49:Applied Algebraic Dynamics.
[11]Knuth D E. The Art of Computer Programming. Reading,MA: Addison-Wesley Publ. Co, 1998, Vol.2: Seminumerical Algorithms (3rd Edition).
[12]Larin M V. Transitive polynomial transformations of residue class rings.Discrete Mathematics and Applications, 2002,12(2): 127-140.
[13]Durand F and Paccaut F. Minimal polynomial dynamics on the set of 3-adic integers.Bulletin of the London Mathematical Society, 2009, 41(2): 302-314.
