基于矩阵秩统计的卷积码分组交织盲识别
2015-01-13李歆昊
陆 凯,张 旻,李歆昊
(1.解放军电子工程学院,安徽 合肥 230037;2.安徽省电子制约技术重点实验室,安徽 合肥 230037)
0 引言
交织器由于能极大限度的改变信息结构,把信道突发错误分散到多个码字中,使纠错码的作用体现出来,被广泛应用于数字卫星广播、深空探测和移动通信等系统中[1]。在非合作对抗领域,对于存在交织的编码数据,想要得到原始信息,首先需要解决交织参数的识别问题,然后才能根据解交织后的数据进行后续的编码识别,最终译码得到原始数据,因此交织的盲识别技术研究对于智能通信以及信息截获领域具有十分重要的意义。
分组交织是交织编码的一种重要方式,对其盲识别研究越来越引起同行的重视,各种识别方法不断涌现。如文献[2]首先提出了基于“秩准则”的分组交织的交织长度的盲识别方法;文献[3-5]在文献[2]的基础上通过引入高斯消元法提高了识别算法的容错性,使之更适用于实际情况;文献[6]提出利用码重分布特性的方法对基于低码率线性分组码的分组交织长度进行识别。但是这些方法仅仅识别了交织长度,没有进一步对交织矩阵的行数、列数进行研究;文献[7]在矩阵分析法获取交织长度的基础上,提出反向纠错思想,穷举条件规定范围内所有可能的分组码和交织模式,识别了交织矩阵的行数、列数以及交织起始点,但是存在运算数据量巨大,识别正确率不高等问题,使得算法使用受限。因此,现有的识别算法难以满足非合作情况下的盲识别需求。本文针对此问题,提出了基于矩阵秩统计的卷积码分组交织盲识别方法。
1 分组交织的基本概念
1.1 分组交织的基本原理
分组交织按一种规则排列成矩阵形式,然后再按另一种顺序读出,从而打乱原有编码序列,重新组合成一组长序列,具体如图1和图2所示。
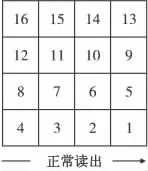
图1 输入数据Fig.1 Input sequence
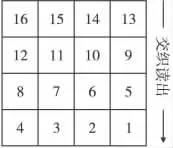
图2 交织数据Fig.2 Interleaved sequence
其交织映射函数可以表示为[9]:

式(1)中,L 为交织长度,n为交织矩阵的列数,mod表示伽罗华域运算。
1.2 卷积码的分组交织的性质
为保证卷积码和分组交织器结合的最优性能,卷积码和分组交织之间满足以下性质[8]:
1)L ≥n(m+1),即交织的长度必须大于卷积码的约束长度;
2)分组交织的长度是卷积码的码长的倍数;
3)交织器的起始点是卷积码的起始点;
4)块内连续性:在分组交织中卷积码的一个码长内的数据一定在一个分组块中,无论怎么变换,也不会使码字变化到另一个分组中,因此,可以利用此性质求解交织长度;
5)块间连续性:相邻的交织块之间具有时间连续性,信息序列变化时也只在本分组块之间变化,所以在恢复交织后,码字之间的约束关系是不变的。
卷积码分组交织的盲识别就是利用这些性质,完成对交织矩阵的行数、列数以及交织起始点的识别。
2 基于矩阵秩统计的卷积码分组交织盲识别
2.1 卷积码分组交织的性质分析和推导
对于接收的卷积码分组交织数据,交织长度为L=m×n,m 和n 分别为交织矩阵的行数和列数。由式(1)可知,在同一个交织矩阵中,同一行中相邻的数据,列读出后的距离变成了交织块的行数m,如图3所示(其中a,b,…,x 不同字母表示不同的交织块)。
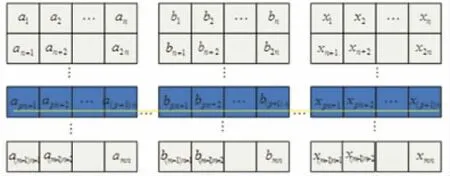
图3 交织采样模型Fig.3 Intertwinedsampling model
由图3可知,在每一个交织块中任意一行的数据 都 是 一 段 连 续 的 卷 积 码 信 息 序 列cpn+1cpn+2…cpn+n。根据(n0,k0,m)卷积码的性质,当信息序列的长度大于卷积码的约束长度时,该信息序列必然存在校验向量HN×1,使得[8]:

式(2)中,N =n0(m+1)为该卷积码的约束长度。由卷积码分组交织的性质可知,每一个分组交织块的起始点都是卷积码的起始点,因此对各交织块的同一行数据,数据的位置与卷积码的位置存在特定的一一对应关系,可以得到:
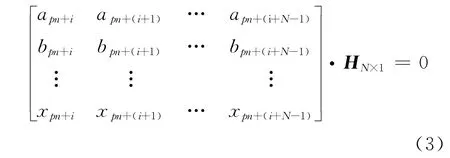
卷积码是一种有记忆编码,当交织矩阵的列数大于卷积码的约束长度时,提取各交织块中同一行数据构成一个p×q矩阵(q>N,p>q),该矩阵具有以下性质:
定理1由连续的(n0,k0,m)卷积码信息序列所构成的p×q矩阵,当矩阵的列数q>n0(m+1),p>q时,若卷积码在矩阵中的位置一一对应,则对该矩阵进行单位化后左上角单位阵维数相等,且此时矩阵的秩不等于列数q[8]。
定理2 对(n0,k0,m)卷积码所构成的p×q矩阵(q>n0(m+1),p>q),如果卷积码的起始点与矩阵每行的起始点重合时,则单位化后左上角单位阵的维数最小[8]。
由定理1和定理2可以推导出,对不同交织块中同一行数据建立的矩阵T 进行单位化处理,化简成 [IkP ]的形式,可得:

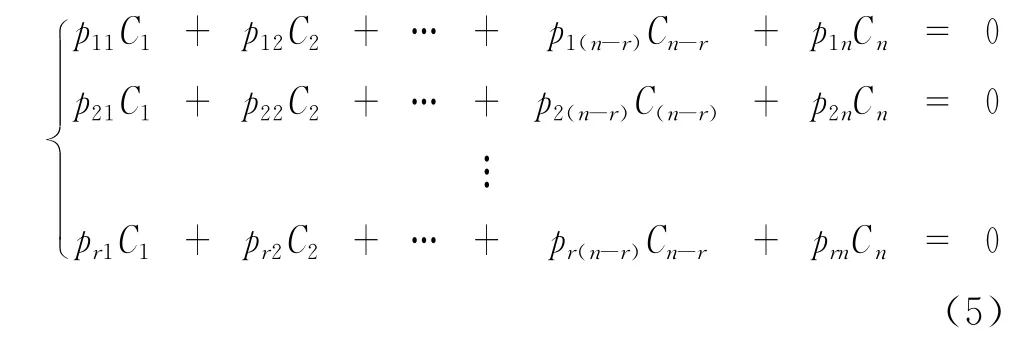
得到该矩阵为非满秩,rank(T)<n。则该矩阵可以得到一组编码约束方程为:
由此约束方程可以得到该段序列中卷积码的校验矩阵HN×1[10]。
2.2 交织参数识别
2.2.1 基于矩阵秩统计的交织矩阵的行和列识别假设交织长度为L=m×n,把交织数据排列成矩阵形式,如图3所示。现对接收数据进行采样处理,当采样间隔为交织矩阵的行数m 时,采样后的序列数据为:
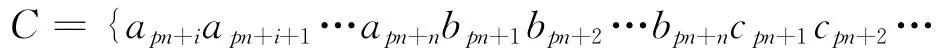
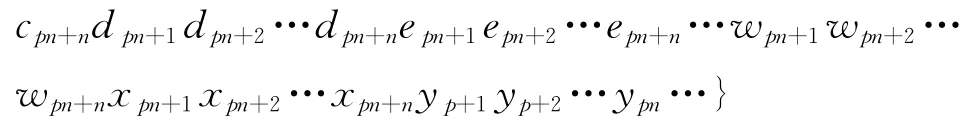
其中a,b,…,x,y,… 不同字母表示不同的交织块;pn 表示交织块中的第p 行;anp+i表示采样数据的起始点。
将序列C 排列成矩阵形式,当矩阵宽度为2n时,会形成如式(6)的矩阵D:

由交织块中的列数为n,以矩阵D 的第一行为例,当矩阵宽度为2n 时,a 交织块中得到的第p 行数据apn+iapn+(i+1)…apn+n排列在矩阵D 中第一行的长度为n-i+1,c交织块中排列在矩阵D 中的数据cpn+1…cpn+(i-1)的长度为i-1,第一行的总长度为2n,所以会存在长度为n的完整的b 交织块中的一行数据bpn+1bp+2…bpn+n。同理,其他行中也存在完整的交织块的一行数据,且这些不同的完整交织块的同一行数据在矩阵D 中的位置相对应,如式(6)中虚线表示的数据,该数据组成的矩阵存在相关列。
根据定理1和式(4)可知D 中虚线所示数据组成的矩阵为非满秩,而非满秩矩阵是矩阵D 的一部分,所以可以推导出矩阵D 也为非满秩。
由此,对交织后的数据进行遍历采样处理并构建矩阵,当构建矩阵非满秩时(即存在相关列),以此采样周期获取的数据构建新的矩阵,新矩阵的列数为非满秩时矩阵列数的周期倍,判别矩阵是否存在相关列,若存在,则此时的采样间隔为交织矩阵的行数,非满秩矩阵列数的周期为交织块的列数,实现了交织长度的识别L=m×n。对矩阵秩统计的求解可以通过高斯消元法来完成的[4]。
2.2.2 交织起始点的确定
2.2.2.1 校验矩阵的求解
将采样后的序列C 排列成矩阵形式,当矩阵宽度为2n 时,会形成如式(6)的矩阵D,可表示为D=[T1,T2,T3]其中:
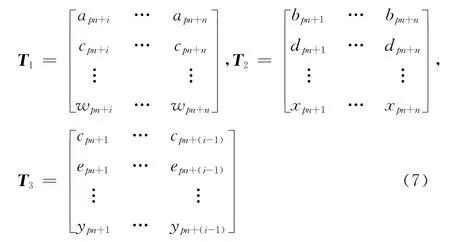
式(1)中,T2矩阵是由完整的不同交织块中相同行组成的数据,为非满秩矩阵,由式(4)可知,T2矩阵可以化简成 [IkP ]的形式。因此在交织矩阵行列识别出来的基础上,可以利用该特性,对矩阵D 进行高斯消元法化简,求解出卷积码的校验矩阵HN×1[10]。
2.2.2.2 起始点的识别
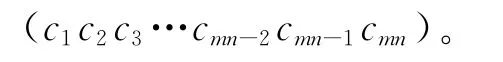
由于交织块的行数和列数已知,假设交织块的行长为m,列数为n,送入L=m×n解交织器进行解交织处理,如:

图4 解交织的模型Fig.4 Deinterleaver model
解交织得到:

C2序列会出现两种情况:
①c1为交织块的起始点
当c1为交织块的起始点,由于交织块的参数已知,因此解交织后就是原始卷积码数据。由卷积码的性质可知,一段约束长度为N 的卷积码数据[ci…ci+N-1]·HN×1=0(其中i表示卷积码的起始点,N 为卷积码的约束长度),因此,利用一个长度为N 的滑动窗(窗内包含N 个序列数据),从解交织后数据起始位开始滑动,滑动窗每次移动的距离为一个卷积码的码长n0,如:
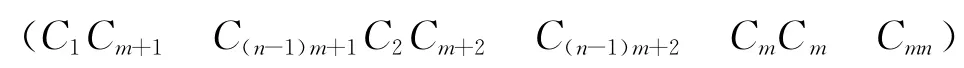
(C1Cm+1…)1×N与校验向量HN×1相乘,得到的值为0。因此通过滑动窗的移动,可以获得周期为码长n0的0序列。
②c1不为交织块的起始点
当c1不为交织块的起始点,长为L=m×n的数据包含两个交织块中的元素,假设该数据如下:

其中a,b不同字母表示不同的交织块。解交织后数据为:
C3= (apn+iapn+i+1…apn+nbpn+1bpn+2…bpn+i-1…
a(m-1)n+ia(m-1)n+i+1…amnb(m-1)n+1b(m-1)n+2…b(m-1)n+i-1…a(p-1)n+i+1a(p-1)n+i+2…apn+nbpn+1bpn+2…bpn+i)
由此可以看出,解交织后的数据中a、b 两个交织块中的元素出现了交叉。由于两个交织块中的数据之间不存在约束关系,利用校验矩阵验证时[apn+i…apn+nbpn+1…bpn+N-n+i-1]·HN×1不 一 定 等 于0。因此利用一个长度N 的滑动窗移动的时候,无法获得周期为码长n0的0序列。
这样就通过遍历交织数据起始位的方法,并用校验向量和滑动窗内数据的乘积能够获取周期性的0输出序列的方法来判别分组交织的起始点。
2.3 识别过程
对交织矩阵的行数、列数以及交织起始点的识别的具体步骤如下:
步骤1对接收的交织数据C0进行采样处理,获取采样序列C;
步骤2 对C 序列遍历构建矩阵,利用高斯消元法求解相关列,判定矩阵是否存在线性约束关系,如果不存在,改变采样间隔,返回步骤1;
步骤3 把C 序列构建新的矩阵,新矩阵的列数为步骤2中存在相关列时矩阵列数的周期倍,判别新矩阵是否存在相关列,如果存在,则此时判断交织矩阵的行数为该采样周期,且此时非满秩矩阵列数的周期为交织块的列数,如果不存在,则改变采样间隔,返回步骤1;
步骤4利用C 序列按交织矩阵的列数的2倍构建矩阵,求解校验向量H,然后截取一段交织后的信息序列,把该序列流的前L 比特数据依次作为交织起始点进行解交织处理;
步骤5 利用一个长度为N 的矩阵框,从解交织后数据起始位开始截取数据与校验矩阵相乘,如果得到的值全为零,得到此时的起始点就是交织起始点,反之,不是起始点。
3 仿真实验
实验中卷积码选取多项式为(15,17)的(2,1,4)非系统卷积码,分组交织选择行数为19,列数为26的交织块,仿真获取交织数据长度为500 000bit,起始点选择为296bit。
实验1:交织矩阵的行数和列数识别
通过遍历采样周期并对采样数据求解线性相关列,结果如图5所示。
由图5可知,在采样值为19时出现相关列,且出现相关列的矩阵的列数为26。按存在相关列时矩阵列数的周期倍构建新的矩阵,求解新矩阵是否存在相关列,结果如图6所示,得到的相关列值如表1所示。
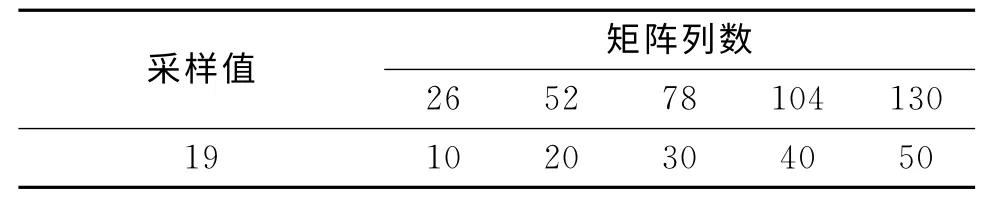
表1 列数与相应的相关列的检测值Tab.1 The number of columns corresponding detection of related column
由表1可知,检测值在[26,52,78,104,130]等列时出现相关列,此时存在相关列的矩阵列数的周期为26。根据论文2.2节分析可以判断最终的交织块行长m 为19,列宽n为26,因此可得交织长度为19×26=494。
实验2:不同误码条件下交织块的行数和列数识别率
实验条件如实验1,改变接收序列的误码率,对本文算法各进行100次蒙特卡罗仿真试验,并与文献[2]的“秩准则”算法进行比较,结果如图7所示。
图6表明,随着误码率的增加,本文算法始终优于文献[2]“秩准则”算法。
实验3:起始点的识别
实验条件如实验1,对获取的交织数据进行交织起始点的识别,识别结果如图8所示。
由图8可知,在高误码率条件下仍然具有很好的交织起始点的识别率。
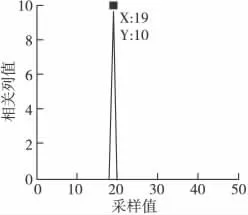
图5 不同采样值下的相关列Fig.5 Related column under different sampling

图6 相关列的检测值Fig.6 Detection of related column of matrix

图7 两种方法的容错性对比Fig.7 Comparison of the two methods of fault tolerance
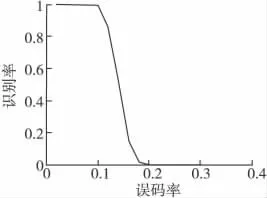
图8 不同误码率条件下起始点的识别率Fig.8 Recognition rate under different starting points BER
4 结论
本文提出了基于矩阵秩统计的分组交织盲识别方法。该方法首先利用分组交织器中相邻的码元交织后距离为交织矩阵的行数的关系,通过对采样后数据进行矩阵秩统计求解交织矩阵的行数和列数,然后采用校验矩阵对解交织后的数据验证的方式识别交织器起始点,实现交织器的盲识别。仿真实验表明该方法有很好的稳定性和鲁棒性,有一定的工程使用价值。
[1]Sung-Joon Park,Jun-Ho Jeon.Interleaver Optimization of Convolutional Turbo Code for 802.16 Systems[J].IEEE Communications Letters.2009,5(13):339-341.
[2]Burel G,Gautier R.Blind estimation of encoder interleaver characteristics in a non-cooperative context[C]//Processing of the IASTED International Conference on Communication,Internet and Information Technology Scottsdale,AZ,USA:ACTA Press,2003:275-280.
[3]Sicot G,Houcke S.Blind detection of interleaver parameters[J].Signal Processing,2009,89(4):450-462.
[4]Sicot G,Houcke S.Blind detection of interleaver parameters[C]//IEEE International Conference on Acoustics,Speech and Signal Processing-Proceedings.Philadelphia,USA:IEEE,2005:829-832.
[5]Lu L,Li K H,Guan Y L.Blind detection of interleaver parameters for non-binary coded data streams[C]//IEEE International Conference on Computing Dresden,2009:1-4.
[6]郑鹏鹏,张玉,杨晓静.基于低码率线性分组码的分组交织长度识别[J].电子信息对抗技术,2012,27(4):9-12.
[7]郑鹏鹏,张玉,杨晓静.基于矩阵模型的线性分组码及分组交织识别[J].计算机工程,2012 38(17):84-86.
[8]张永光,楼才义.信道编码及其识别分析[M].北京:电子工业出版社,2010.
[9]刘东华,梁光明.Turbo码设计与应用[M].北京:电子工业出版社,2011.
[10]杨晓静,刘建成,张玉.基于求解校验序列的(n,k,m)卷积码盲识别[J].宇航学报,2013,34(4):568-573.
