基于改进二叉树支持向量机的多故障分类算法

李伟伟，王 莉，张 琳，刘 进

（1.空军工程大学防空反导学院，陕西 西安 710051；2.解放军95425部队，云南 曲靖 655000）

0 引言

支持向量机（SVM）是基于统计学习理论的新学习方法［1］，最初用于解决二值分类问题，但现实中多分类问题居多。因此，将二值分类算法推广到多分类领域是当前SVM 研究的重要内容之一［2］。SVM 的多分类扩展策略主要分两大类：一是整体优化法，将所有SVM 参数优化在一个公式中，该方法求解复杂，解决多分类问题很少应用；二是组合学习法，将SVM 按不同策略组合成多类分类器，例如一对多法、一对一法、决策导向无环图法和二叉树法等［3］。一对多法运算量过大，一对一法所需SVM数目过多，决策导向无环图法存在决策偏好的问题，二叉树法结构的设计会影响多类分类器的分类精度［4］。

目前，对于二叉树支持向量机算法结构设计的问题已有一定研究。文献［5-6］根据各类样本在高维特征空间的分布情况设计分类顺序，分布范围广的类型首先被识别，就是先把样本空间中最容易识别的类型识别出来。另外，一种依赖类别优先级的多类分类器可根据各类型发生频率的高低排序确定二叉树的结构，即发生概率较高的类别先被识别出来。但上述算法仅考虑了某一种影响因子对分类精度的影响，不够客观、全面，因此分类器的结构不能使分类精度达到最优。本文针对上述问题，提出了将AHP和二叉树SVM 相结合的多故障分类算法。

1 AHP和二叉树SVM 的基本原理

1.1 AHP

层 次 分 析 法（Analytic Hierarchy Process，AHP）是美国著名运筹学家Satty 等人于20 世纪70年代提出的一种定性与定量分析相结合的多准则决策分析方法。基本思想是把决策问题的相关元素按照支配关系形成层次结构，将评估目标分解成一个多级指标，并通过引入1～9的比例标度对各个因素的相对重要性给出判断［7］。表1 为不同比例标度的含义。

表1 判断矩阵的比例标度Tab.1 Proportion scale of judgment matrix

层次分析法通过将复杂问题分解为若干层次和若干因素，在各因素之间进行简单的比较和计算，得出不同方案的权重，为最佳方案的选择提供依据［8］。实施步骤主要有明确问题，建立递阶层次结构，构造判断矩阵，计算权重值，进行一致性检验，得到各方案对总目标的权重值。

层次分析法不仅能够综合考虑评价体系中各层因素的重要程度使各指标权重趋于合理，而且更大的优势在于能够充分利用专家的主观意见。

1.2 二叉树SVM

二叉树SVM 分类原理如下：首先通过构造二叉树将多分类问题分解成一系列二值分类问题，然后使用SVM 实现二分类。二叉树SVM 进行训练和测试时，从根节点的SVM 开始分类，按照一定的分类顺序依次识别。假如有1，2，…，k种模式，对k种模式进行分类，需k-1个SVM，结构如图1所示。

图1 二叉树SVM 结构Fig.1 Structure of binary tree SVM

二叉树SVM 对于测试样本无需经过所有二值分类器，只要识别出类别即可停止运算，从而节省了测试时间。在图1 所示分类器中，第1 个SVM 用于将第1类从1，2，…，k 类别中区分出来，第2 个SVM 将第2类从2，3，…，k 类别中区分出来，依此类推，直到第k-1 个SVM 将最后两个类别区分开。图1所示分类器只是许多分类策略中的一种，分类顺序为1，2，…，k，共有k！种分类顺序，分别对应k！种结构，不同的二叉树结构决定了不同的分类精度。将分类器用于模式识别时，可通过合理设计二叉树的结构提高分类器的分类精度。

2 基于AHP和二叉树SVM 的算法

基于AHP 和二叉树SVM 的多故障分类算法中，AHP综合多个指标衡量所有故障的价值度，对每一类故障得出一个权重值，权重大小决定了故障识别的先后顺序，基于此顺序构建二叉树SVM 的结构。

2.1 结构设计对分类精度的影响

二叉树支持向量机的结构并不是唯一的，不同的结构会导致不同的分类结果和分类精度。结构设计如何影响分类精度，下面简单分析之。

以图1为例，假设各层划分正确率分别为p1，p2，…，pk，类别划分正确率为l，则所有故障类别的划分正确率为：

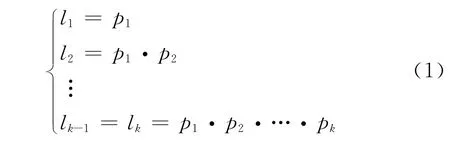
由式（1）可得

即二叉树分类器越底层，SVM 识别正确率越低；而且下层SVM 识别率依赖于上层，只有使上层SVM 识别正确，下层SVM 的识别率才能得到保证。

基于此特点，只有保证识别率高的类别处于分类器上层，才能总体上提高整个分类器的分类精度。先将样本空间中最易被分割的类识别出来以及采用最大投票机制算法构造二叉树都是基于此原因。

因此，本文改进算法通过建立一套评价体系为各类别设定权重值，根据权重值对所有类别排序，使权重大的类别处于分类器的上层，符合上述特点。这样确定下来的二叉树结构依赖于各个类别的权重量，相比较随机确定的二叉树结构，具有更好的分类性能。

2.2 基于AHP和二叉树SVM 的多故障分类算法

为了便于问题说明，直接以发电机轴承的故障诊断作为案例阐述改进算法，主要步骤如下：

1）建立层次结构

对于电机轴承的故障诊断问题，在高维特征空间中，影响分类精度的因素主要有类内样本分布范围、类间样本分布距离等因素。其中，类内样本分布范围指同一类别样本在高维特征空间的分布范围，范围越大，被识别的概率越高；类间样本分布距离指在高维特征空间中，不同类别分布范围之间的距离，两者距离越大，越容易被分割开。结合实际经验进行诊断时，还需要考虑故障发生概率、诊断故障后的挽回损失等。

层次分析法模型分为目标层、准则层和方案层，其中，目标层为故障的价值度；准则层为衡量故障的影响因子：各种故障在高维特征空间的样本分布范围B1，故障发生的频率B2，诊断挽回的损失B3以及各类故障在高维特征空间样本的类间分布距离B4，多个影响因子的选择使得到的权重是故障识别率，实际发生概率，理论分割难易程度的集中体现；方案层故障状态包括：正常、内圈故障、外圈故障、滚珠故障。层次结构如图2所示。

2）构造判断矩阵

为把定性分析的结果量化，将同层次元素对于上层某一准则的重要性进行两两比较，构造判断矩阵

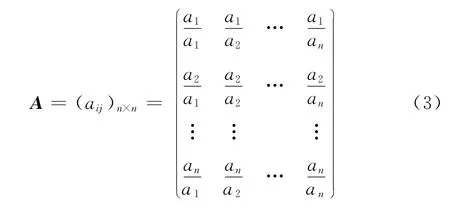
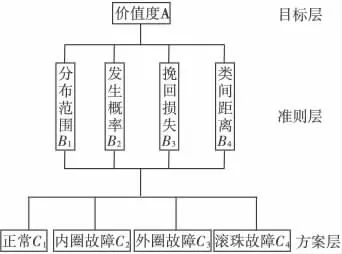
图2 轴承故障诊断的层次结构图Fig.2 Hierarchical structure of bearing fault diagnosis

式（3）中，aij是元素ai和aj相对于准则层的重要性的比值，判断矩阵A 具有下列性质：

同层次元素的重要程度如何，根据表1中程度的不同按1～9的比例标度赋值。本文轴承故障中，基于诊断经验构造准则层B 相对目标A 的判断矩阵为：

3）计算权重值

用判断矩阵求权重的方法有很多种，包括和法、最小夹角法和特征向量法等，本文使用特征向量法。首先，计算判断矩阵A 的最大特征值λmax；然后，根据式（6）求相应正特征向量（分量全大于0的特征向量）。

式中，λmax为矩阵A 的最大特征值，W 为其特征向量，将其进行归一化处理，即得权重向量。

经计算，A 的最大特征值为λmax=4.043，权重向量为W（A）= （0.520，0.201，0.201，0.078）。

4）矩阵的一致性检验一致性检验的步骤：

①计算判断矩阵的一致性指标

②从表2中查找平均随机一致性指标RI

表2 平均随机一致性指标Tab.2 Random index

③计算一致性比例CR

若CR＜0.1，认为A 具有满意的一致性，接受A；否则，放弃A 或对A 的数据做适当调整。经检验得CR=0.016＜0.1，表明具有可接受的一致性。

5）计算合成权重

上述计算得到的只是准则层B 中各元素相对目标A 的权重向量，最终目的是要得到方案层C 中各元素对于目标A 的权重向量。因此，分别构造方案层对于准则层元素的判断矩阵B1，B2，B3，B4，然后按上述方法计算权重向量得

则合成权重为：

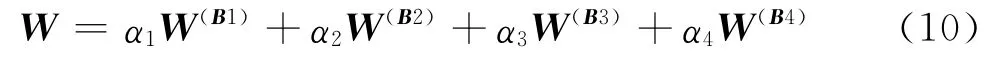
式（10）中，α1、α2、α3、α4分别为W（A）的四个分量，得W = （0.151，0.238，0.210，0.401）。经矩阵的一致性检验得CR=0.024＜0.1，由此说明合成权重具有良好的一致性。

6）确定二叉树SVM 的结构

依据上述故障的权重值对故障类型进行排序，权重值大的类型优先诊断，保证将权重值大的类别首先识别出来。

改进算法将AHP和二叉树SVM 结合起来，充分利用AHP的主观优势确定权重，为模型结构的建立提供依据。克服了AHP过分依赖专家主观判断的缺点，同时弥补了二叉树SVM 不能反映决策者偏好的缺陷。两种算法的结合能够充分发挥各自的优势，克服算法本身存在的缺陷。

3 仿真验证

故障诊断过程主要包括故障特征提取和模式识别两大步骤，利用小波包分解得各频带分量的能量，归一化处理得到特征向量，将其作为SVM 的输入进行故障模式识别。下面将改进算法用于发电机轴承的故障诊断，诊断模型如图3所示。

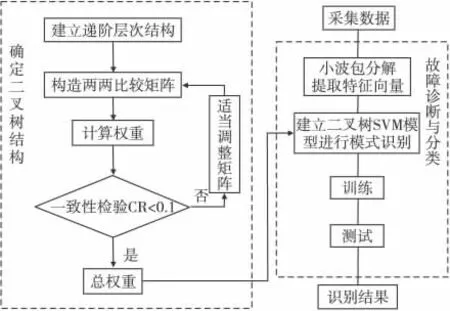
图3 基于AHP和二叉树SVM 的诊断模型Fig.3 Diagnosis model based on AHP and binary tree SVM

3.1 特征向量的提取

对于正常、外圈故障、内圈故障和滚珠故障4种状态各提取50组样本数据，其中40组用于训练，另外10组用于测试。处理和提取故障特征向量的步骤如下：

1）本文实验所用的实测轴承振动数据来自美国凯斯西储大学的电气工程实验室［9］。如图4 所示为一组不同故障状态下的样本图。

2）采用db3小波对振动信号进行3层小波包分解，得到8个子频带的小波包分解系数。以一组外圈故障信号为例进行小波包分解，如图5所示。

3）计算图5中8个频带的能量值，进行归一化处理得故障的特征向量如式（11）。

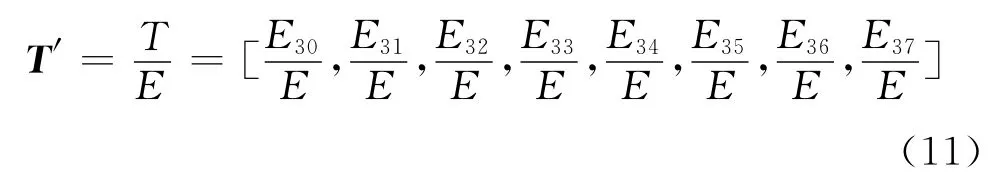
式（11）中，E3i（i=0，1，…，7）为各频带能量值，E 为能量总和。

4）重复上述步骤，提取多组特征向量。

3.2 多类分类器的构造

建立故障样本集：（xi，yi），xi∈R8为样本输入，yi∈｛1，2，3，4｝为样本输出，代表四种故障类型，i=1，2，3，4。

由合成权重W = （0.151，0.238，0.210，0.401）判断轴承故障诊断的顺序为：滚珠故障、内圈故障、外圈故障、正常。所以二叉树SVM 诊断结构如图6所示。

图4 振动时域波形图Fig.4 Vibration time-domain waveform

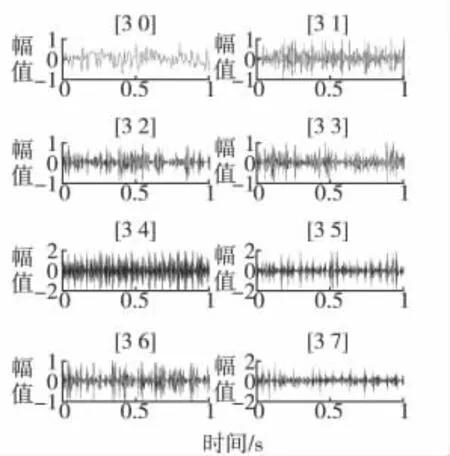
图5 小波包分解图Fig.5 Wavelet packet decomposition

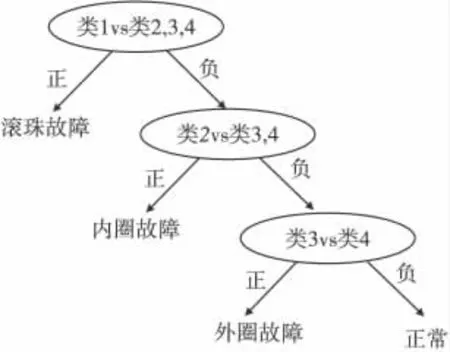
图6 二叉树SVM 诊断结构图Fig.6 Diagnosis structure of binary tree SVM

3.3 故障模式识别

建立二叉树SVM 的结构后，进行故障模式识别，步骤如下：

1）确定影响SVM 分类性能的参数。本文SVM 的核函数选取径向基核函数（RBF）

式（12）中，δ为核宽度。此外，需确定惩罚因子c。

参数δ和c 的选择直接影响SVM 的分类精度和泛化能力。为确保快速有效地寻找最优参数（δ，c），采用遗传算法寻优得到参数组合（4，224）。

2）输入训练样本，完成训练过程。

3）将测试样本输入训练好的二叉树SVM，检验识别能力。

4）在相同的样本数据和参数设置的前提下，运用不同多分类算法进行故障诊断。

将各类算法进行故障诊断的结果进行统计，对比结果如表3所示。其中M1代表本文算法，M2与M3均代表二叉树SVM 算法，M2算法中二叉树的结构根据故障频率设计，M3 算法中二叉树的结构根据样本分布范围设计，M4代表一对多法，M5代表一对一法，M6代表决策导向无环图法。

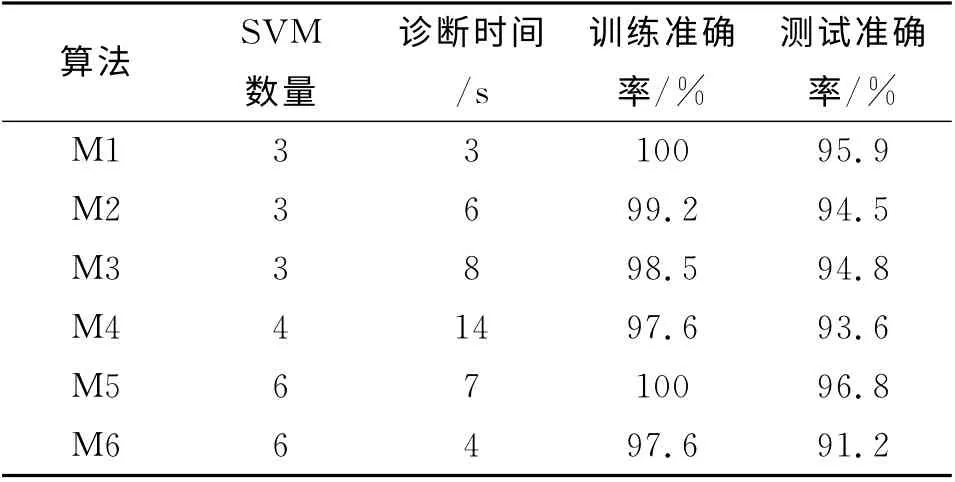
表3 不同多分类算法诊断结果统计Tab.3 Diagnosis statistics of different classification algorithms

通过表3中的对比数据可知，一对一法诊断准确率最高，达到96.8%，但耗时相对较长；其次为改进算法，诊断准确率为95.9%，同时改进算法诊断时间短，需要的SVM 数量少，这一点有利于SVM的推广。与另外几种算法作比较，改进算法无论在诊断准确率和诊断时间方面均占优势。因此，综合多个衡量指标，基于AHP和二叉树SVM 的多故障分类算法优于其他几种算法。

4 结论

本文提出了将AHP 和二叉树SVM 相结合的多故障分类算法。该算法综合考虑了影响分类精度的多个影响因子，运用层次分析法计算各类故障的权重，根据权重值设计了多类分类器的结构。仿真验证表明，该算法适合进行多类故障诊断，相比较一对一法、一对多法等算法诊断效率更高，诊断精度更好，推广应用前景较广。

［1］统计学习理论的本质［M］.张学工，译.北京：清华大学出版社，2000.

［2］胥永刚，孟志鹏，陆明.基于双树复小波包变换和SVM的滚动轴承故障诊断方法［J］.航空动力学报，2014，29（1）：67-73.

［3］W idodo A，Yang B S.Application of nonlinear feature extraction and support vector machines for fault diagnosis of induction motors［J］.Expert Systems with Applications，2007，33（1）：241-250.

［4］康守强，王玉静，姜义成，等.基于超球球心间距多类支持向量机的滚动轴承故障分类［J］.中国电机工程学报，2014，34（14）：2319-2325.

［5］袁胜发，褚福磊.次序二叉树支持向量机多类故障诊断算法研究［J］.振动与冲击，2009，28（3）：51-54.

［6］赵海洋，徐敏强，王金东.改进二叉树支持向量机及其故障诊断方法研究［J］.振动 工程学报，2013，26（5）：764-770.

［7］谢金明.水库泥沙淤积管理评价研究［D］.北京：清华大学，2012.

［8］梁晨.子午线轮胎综合接地性能评价体系与方法研究［D］.镇江：江苏大学，2013.

［9］The Case Western Reserve University Bearing Data Center Website.Bearing Data Center Seeded Fault Test Data［EB／OL］.［2007-11-27］.http：／／www／eecs／cwru／edu／laboratory／bearing／.