温度应力下微陀螺仪的加速寿命评估
2015-01-13于丽霞王淑英吉腾飞鲍爱达
于丽霞,秦 丽,王淑英,吉腾飞,鲍爱达
(1.中北大学电子测试技术重点实验室,山西 太原 030051;2.中北大学信息与通信工程学院,山西 太原 030051;3.中北大学仪器与电子学院,山西 太原 030051)
0 引言
硅微机械陀螺仪作为惯性导航系统的关键器件之一,通常与弹体同步装配,记录弹体的动态信息。在实际应用环境下,常伴随高温、温变、瞬态高温等恶劣环境,而制作微陀螺仪芯片的硅材料的物理特性受温度变化影响显著,从而会影响微陀螺仪的标度因数和零偏等参数,造成测试弹体信息的精确度下降。为此,开展模拟恶劣温度环境的可靠性试验与评估研究不容忽视。目前,国内外对微机械陀螺仪的研究大都是针对误差补偿以提高输出精度为目的,而对其在恶劣环境下的失效模式、失效机理以及可靠性试验和评估的研究较少[1-5]。本文针对此问题,提出了温度应力下微陀螺仪的加速寿命评估方法。
1 微陀螺仪的工作原理及敏感应力分析
1.1 工作原理
硅微机械陀螺仪的结构形式各不相同,但都包含驱动模块和检测模块两部分,其中静电驱动、电容检测方式最为常见。图1所示为工作原理示意图,驱动质量块和检测质量块在静电力作用下沿x 驱动方向振动,当垂直于x 和y 方向所在平面的z 方向有角速度输入时,根据哥氏效应,检测质量块会沿y 方向运动,通过检测质量块在y 方向的位移变化量即可获得z 方向的角速度大小[6]。
1.2 敏感应力分析
环境对微陀螺仪的测试精度影响较大,如:振动、温度、电磁干扰和气压变化等都会对陀螺仪的输出造成一定程度的影响。根据典型微陀螺仪的工作原理和结构特点,采用故障树(FTA)方法确定微陀螺仪的薄弱环节和敏感应力。由故障树的编制规则[7],以顶事件“陀螺仪失效”作为“树根”,按可能的失效模式自上而下依次分解,如图2所示。
微陀螺仪的失效模式包括零偏、零偏稳定性差、输出精度差和性能退化。在多个描述陀螺仪的参数中,最基本和最重要的参数是零偏和零偏稳定性,因此将二者变化大确定为主要失效模式。由于陀螺材料容易受环境温度的影响,尤其在工作中会受到瞬态高温应力时,不但结构尺寸发生变化,且其弹性模量、残余应力等性能也会变化。当超出使用温度范围,其各方面的性能均会发生变化,最终导致微陀螺仪失效[8]。因此,本文将温度作为敏感环境应力研究单应力环境下的微陀螺仪可靠性问题。
2 温度应力下加速寿命评估理论
温度应力下加速寿命评估理论主要包括三部分:一是通过步进温度应力试验和恒定应力试验获取高应力下的失效寿命数据;二是对失效数据分布假设检验选择最优的分布形式估计参数,并验证加速试验过程中失效机理的一致性,从而采用阿伦尼斯模型建立加速寿命评估模型;三是根据建立的加速寿命评估模型对微陀螺仪的正常使用环境中的寿命情况进行评估,其理论框图如图3所示。
开展加速寿命试验是整个加速寿命评估理论的首要任务,因此加速试验的方案设计应满足三个条件[9]:失效机理的一致性,失效过程的规律性和失效分布的同一性,而且试验结束后还要根据估计的参数值证明失效机理的不变性。

图2 微陀螺仪的故障树Fig.2 The fault tree of Micro-gyro

图3 加速寿命评估理论框图Fig.3 The diagram of acceleration life evaluation
3 温度应力下微陀螺仪的加速寿命试验
3.1 高温步进应力试验
本文以某型号数字微机械陀螺仪为研究对象,对5个样本进行了高温步进应力试验,起始温度为50 ℃,步长为10 ℃,温度变化率采用最大速率,每个温度段达到稳定后开始性能测试,试验直至找到被测样本的工作极限。
以微陀螺仪的零偏作为失效判据,当温度上升至110 ℃时,其零偏值变化较大。温度上升到120℃时,零偏值发生阶跃性变化,再将温度降低至110℃进行复测,陀螺仪的零偏仍然异常。因此,判定在高温应力下微陀螺仪的工作极限是110 ℃;对测试数据进行拟合,结果如图4所示,环境温度变化对微陀螺仪的零偏造成一定影响,因此出现零偏随温度漂移的现象,当温度达到120℃时,微陀螺仪的零位输出值突变,陀螺仪失效。
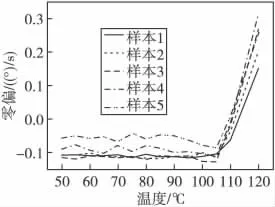
图4 零偏与温度的关系Fig.4 The relationship between null bias and temperature
3.2 高温恒定应力试验
根据高温步进应力试验确定的工作极限确定三个温度恒定应力量值,分别为75℃、85℃和95℃。在三个恒定温度应力环境下,微陀螺仪的失效时间如表1所示,t1—t5分别表示3个应力下5个样本的失效时间。
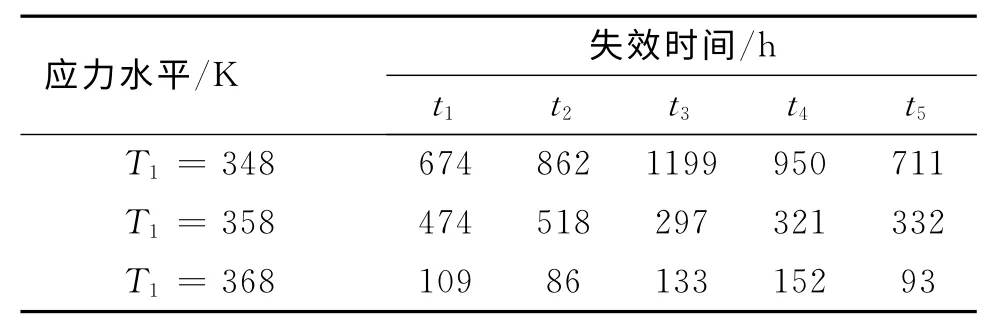
表1 微陀螺仪在各温度应力下失效时间表Tab.1 Failure time under different stress for Micro-gyro
4 温度应力下微陀螺仪的寿命评估
4.1 分布假设检验
对表1中的失效寿命数据进行分布假设检验,尽量选择拟合优度统计量值较小的分布,正态分布和Weibull分布的AD 值分别是2.332和2.440,如图5所示为这两种分布的概率图,失效寿命时间基本分布在一条直线上,而且Weibull分布时不同应力下的直线近似平行,正态分布计算过程较简单,验证了微陀螺仪在加速试验的过程中其失效机理没有发生变化,符合加速寿命试验的基本假设。

图5 失效寿命的分布检验结果Fig.5 The distribution fit test of failure time
4.2 建立加速模型
根据表1列出的三个恒定应力下试验样本的失效时间,运用统计方法计算得到Weibull分布和正态分布参数估计值,如表2和表3所示。

表2 Weibull分布的参数估计值Tab.2 Parameter estimation of Weibull distribution
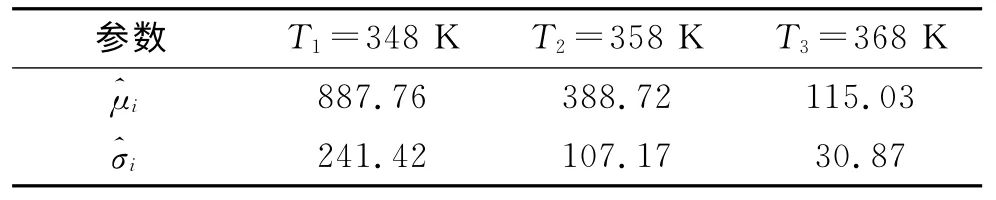
表3 正态分布的参数估计值Tab.3 Parameter estimation of normal distribution
通过参数估计值可以看出,Weibull分布的形状参数基本一致,正态分布的均值和均方差比值基本一致,因此采用Arrhenius温度模型[10]分别建立均值、均方差和尺度参数的加速模型,如图6所示,其表达式为:
lnμ=-30.7+13 058.2/T,lnσ=-32.2+13 140.6/T,lnη=-30.5+13 055.6/T。
4.3 寿命评估
根据3.2求得的加速模型,外推正常使用条件(T0=25+273.15 K)下微陀螺仪失效寿命服从Weibull分布的参数为:
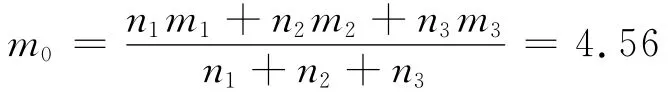
η0=exp(a+b/T0)=5.85×105
可靠度函数为:

当样本寿命服从正态分布时,外推出计算得到的参数为μ0=4.87×105,σ0=1.43×105。在给定的时间t,微陀螺仪的可靠度函数为:
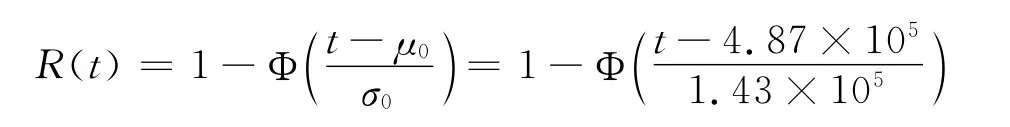
图7所示为微陀螺仪样本服从Weibull分布和正态分布时的可靠度曲线。可以看出,两种假设分布得到的可靠度曲线形状比较接近,验证了采用两种分布形式进行寿命评估的可行性。但结合应用需求,应尽量选择保守的评估结果,对比本文选择两种分布形式得到的评估结果,应选择数据服从正态分布形式的评估结果,即选择拟合度最优的分布形式得到的评估结果较保守,适用于较高的应用场合。对于应用要求不高的场合可以选择Weibull分布的评估结果。

图6 加速模型Fig.6 The acceleration model

图7 不同分布情况的微陀螺仪可靠度曲线Fig.7 The reliability curve of different distribution for micro-gyro
5 结论
本文提出了温度应力下微陀螺仪的加速寿命评估方法。该方法首先要确定试验满足加速性的假设条件,根据样本的工作极限确定高温恒定应力试验方案;然后对试验数据分布假设检验选择拟合度较好的分布形式进行参数估计,证明加速试验过程中失效机理的一致性,从而建立正确的加速寿命模型;最后利用建立的加速模型评估微陀螺仪在正常使用环境中的寿命情况。通过对微陀螺仪样本开展的试验和对评估结果的分析表明:该方法的步骤简捷、正确可行,为微陀螺仪在实际应用中提供了重要的参考依据。
[1]Giorgio De Pasquale,Aurelio Somà.Reliability Testing Procedure for MEMS IMUs Applied to Vibrating Environments[J].Sensors,2010,10:456-474.
[2]Bazu M,Galateanu L,Ilian V.About using combined stresses for reliability testing of Microsystems[C]//Proceedings of the International Semiconductor Conference,2009.
[3]刘凤丽.静电驱动微机械梳状陀螺仪中典型结构的可靠性研究[J].探测与控制学报,2007,29(1):72-75.
[4]陈循.可靠性强化试验与加速寿命试验综述[J].国防科技大学学报,2002,24(4):29-32.
[5]满海鸥.硅微陀螺模态频率温度特性的研究[J].传感技术学报,2009,22(8):1117-1121.
[6]刘宇.固态振动陀螺与导航技术[M].北京:中国宇航出版社,2010.
[7]马静,卢荣翠,李晓阳.基于故障树分析的光纤陀螺用探测器组件可靠性分析[J].中国惯性技术学报,2008,16(4):497-501.
[8]刘加凯.温度应力对MEMS 器件分层失效的影响规律[J].电子元件与材料,2013,32(3):84-87.
[9]Jinsuk Lee,Rong Pan.Analyzing step-stress accelerated life testing data using generalized linear models[J].IIE Transactions,2010,42(8):589-598.
[10]袁宏杰.加速度计贮存寿命与可靠性的步进应力加速退化试验评估方法[J].中国惯性技术学报,2012,20(1):113-116.
