结构设计的几种可靠度计算方法对比

刘连杰，张劲松，贺渝

（1重庆市建筑科学研究院，重庆 401147；2中国建筑科学研究院，北京 100013；3重庆市渝北区建设工程质量监督站，重庆 401120）

0 引言

结构设计属于非定值问题，其不定性可能是由参数的随机性以及计算模型的理想程度等引起的。所以，结构设计必须引入概率论的观点，出于对工程结构中存在的各种不确定性因素的认识，结构可靠性理论应运而生。

20世纪40年代，可靠度概念开始应用于结构设计中。1969年美国学者柯涅尔（Cornell）提出了与结构失效概率相联系的可靠度指标，作为衡量结构安全度的一种统一数量指标，并提出了比较系统的一次二阶矩的设计方法，使结构安全度理论开始进入实用阶段。直到1976年，西德的拉克维茨（Rackwitz R）和菲斯勒（Fiessler B）等人提出改进的验算点方法以后，使考虑分布类型的结构可靠度计算进入新的阶段。它经过系统改进后作为结构安全度联合委员（JCSS）的文件（结构统一标准规范的国际体系第一卷）附录推荐给土木工程界[1]，也称JC法。

1946年，物理学家冯·诺依曼等人通过电子计算机随即模拟了裂变物质的中子连锁反应，其所用的随机模拟方法称为蒙特卡罗法。因此该法成了随机模拟方法的代名词，并被广泛应用至今。经过之后的发展，蒙特卡罗法已成为通过随机模拟来对自然客观现象进行研究的一种方法。随着计算机技术的不断发展，用数值模拟法来计算结构的失效概率已有取代一阶二次矩法的趋势。主要有：直接Monte Carlo法、重要抽样法[2]和改进样本法。普通的直接Monte Carlo法计算精度与计算时间存在矛盾，Shinozuka[3]于1983年率先将重要抽样方法应用于结构可靠性分析，尽可能减少了模拟抽样数，提高了计算效率。

响应面法（Response surface method，RSM）[4]最早是由Box和Wilson在 1951年提出；用于利用统计学的综合试验技术处理复杂系统的输入（基本变量）和输出（系统响应）之间的转换关系，用响应面函数（RSF）来拟合原有的隐式极限状态函数。1984年Wong首次提出结构可靠度计算的响应面法，并于1958年将其应用于土坡稳定的可靠度计算。Bucher等于1990年将响应面法引入结构可靠性分析中，建立结构输入与结构响应之间的关系，然后进行结构可靠性分析[4]。

在一次二阶矩方法中，必须对非正态随机变量进行当量正态化，产生的误差随机变量随非线性程度的增加而提高，因此学者们提出了一种避免将随机变量当量化，而直接计算可靠度指标的方法。Breitung K.W在1994出版的著作中详细介绍渐近积分的方法[5-6]。

1 算法原理

1.1 Monte Carlo直接抽样法

Monte-Carlo法又称随机抽样技巧、概率模拟方法。其理论基础是大数定律，基本思想是通过某种“试验”的方法，得到某件事件出现的频率，或者这个随机变数的平均值，并用它们作为问题的解[7-8]。其特点是模拟的收敛速度与基本随机向量维数无关，模拟过程与功能函数复杂程度无关，无需进行功能函数线性化或随机变量的当量正态化，因此其应用范围基本无限制。

对于失效概率较低或抽样次数n较小的情况，结构失效概率Pf值有相当的不确定性，但这可以通过增加模拟次数来解决。其缺点就是模拟次数相对很大，且获得的信息有限，无法得到灵敏度系数和验算点信息，所以该法在实际上较少运用，一般作为检验其他方法精度的指标。

1.2 Monte Carlo重要抽样法

重要抽样法与直接抽样法原理无本质上的区别，只不过改变了抽样的重心，将抽样的重心转移至对结构失效概率贡献最大的区域，这样可以减少抽样次数，并获得精度较高的解[9]。

设构件失效概率为：

式中X={X1,…，Xn}T，为n维随机向量；fx(x)为X的联合概率密度函数；Df为失效区域。设

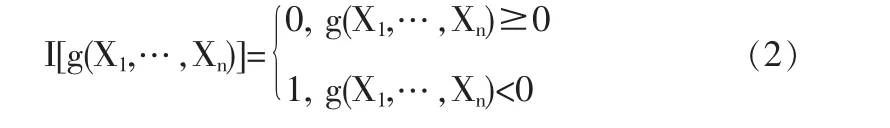
则（1）可表示为：

式中萃为X的定义域。

取hx(x)为重要抽样密度函数。作为概率密度函数，hx(x)满足：

显然，式（3）可表示为：

根据概率论有关随机变量函数数学期望的定义，显然，Pf可以视作随机变量Y的数学期望μY。其无偏估计为：

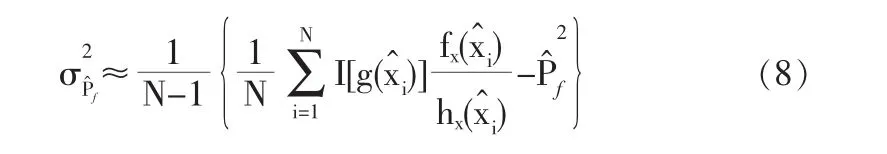
1.3 JC法

JC法适用于随机变量为任意分布下工程结构可靠度指标的求解。因其通俗易懂，精度能满足工程实际需求而被国际“结构安全度联合委员会”（JCSS）所采用。JC法的基本思路是：将非线性功能函数在验算点处（失效边界）作泰勒级数展开，保留至一次项。然后首先对随机变量进行当量正态化[10]，把原来的非正态分布用正态分布代替，以近似计算平均值和标准差。随机变量分布当量正态化后，即可与改进一次二阶矩法的计算过程一样，用迭代法来求解结构的可靠指标。

当量正态化要求在设计验算点坐标处，对于代替的正态分布函数值（CDF）和概率密度函数值（PDF）都和原来的分布函数的CDF值和PDF值相等。 即：

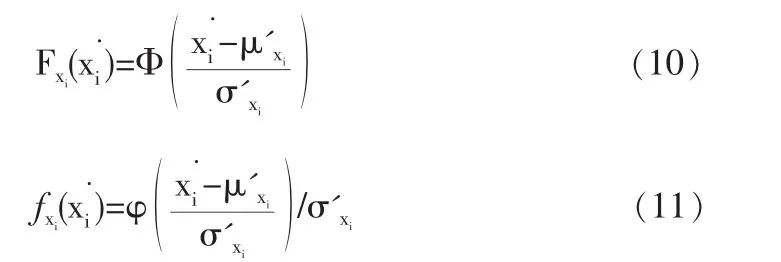
式中μ'xi，σ'xi分别表示等效正态变量X'i的均值、均方差。

利用式（10）和（11），可求得等效正态变量X'i的均值、均方差为：

式中Φ-1(·）为标准正态分布函数的反函数。

JC法适用于随机变量为任意分布的功能函数，计算速度快，计算精度能满足工程需要，有一套固定的程序步骤，适合一般工程技术人员应用。但其局限性在于：将极限状态方程在验算点处进行泰勒级数展开，可能会带来显著性的误差，非正态随机变量的当量正态化也会带来误差。

1.4 响应面法

对于某些复杂的结构系统，随机变量之间可能不存在明显的解析式或是高度非线性，此类问题不可能预先确定分析模型，响应面法为解决复杂结构系统的可靠度分析提供了一种可靠的建模及计算方法。该方法用包含未知数的已知函数代替隐含或复杂的函数，用插值回归的方法确定位置参数，插值点的确定一般以试验设计为基础，若随机变量个数较多则试验次数也会增多[11]。其优势在于：一般可以用二次多项式代替大型复杂的功能函数，并通过迭代插值展开点和系数进行调整，一般都能满足工程精度的要求，具有较高的计算效率。

1.5 一次渐进法

在一次二阶矩方法中，必须对非正态随机变量进行当量正态化，产生的误差随随机变量非线性程度的增加而提高，因此学者们提出了一种避免将随机变量当量化，而直接计算可靠度指标的方法。由于对失效概率的贡献主要是在结构失效最大可能点附近的积分，因此只要将积分局部化，集中在该点附近的失效域内进行，就能够得到失效概率积分的近似结果。

在失效概率最大可能处，将基本变量概率函数的对数展开成泰勒级数并取至二次项，将功能函数也作为泰勒级数展开，用所得超切平面或二次超曲面来逼近实际失效面，再利用一次二阶矩和二次二阶矩法即可完成失效概率的渐近积分[12-13]。

渐进积分法无需进行空间变换，不用变量的累积分布函数，但要计算基本随机变量概率密度函数的一阶和二阶导数，使程序显得很繁琐，但由于避免当量正态化，故而计算精度有所提高。

2 算法性能比较

2.1 变量类型的影响

为评估四种变量类型对各算法性能的影响，构造功能函数：

各变量的统计参数均为：

依次假定X1和X2服从正态分布、对数正态分布、极值I型分布以及Weibull分布，分别采用5种方法计算结构的可靠度指标，结果见表1。本文以100万次Monte Carlo直接抽样模拟的结果作为标准解，以计算值与标准解的比值作为精度指标，结果见图1。

从计算结果可以看出：（1）变量服从正态分布时，各算法的解与标准解十分吻合，这是由于此种情况下，既没有进行变量的当量化，也没有进行功能函数的线性化；（2）变量服从对数正态和极值I型分布时，各算法虽不能完全与标准解吻合，但精度也较好，误差在2%以内；由于此时的功能函数为线性，且未考虑统计参数的影响，因此尚不能得出各算法在对数正态和极值I型分布变量的精度很好的结论；（3）变量服从Weibull分布时，各算法的精度相对较低，特别是重要抽样法，在此时精度最低，但在其他变量类型时均具有极高的精度。这是因为程序算法中fp（即）的模拟并不理想，还有就是程序中验算点的解并不精确。这说明，由于Weibull本身的特征，导致这种在最大失效概率处抽样的方法具有很大的不确定性，经验证，两次抽样的结果误差较大；（4）变量服从非正态分布时，JC法与响应面法十分吻合，且精度优于一次渐进法，说明将线性功能函数近似成二次多项式和将变量当量正态化这两种处理方式在此时具有相同的效果。至于渐进法精度相对JC法较低的原因是：虽然二者均在验算点处进行泰勒级数展开，但渐进法是在最大可能失效处进行积分，故而计算出的失效概率较小，可靠度指标偏大。

表1 各变量类型的可靠度指标计算结果

图1 各算法可靠度指标与标准解比较

综上可知，在线性功能函数的条件下，对于正态变量，选用任意算法均可得到高精度解；非正态分布变量中，Weibull分布对各算法的精度影响最大；线性功能函数情况下，JC法、响应面法结果吻合，一次渐进法精度略差。

2.2 非线性程度影响

为讨论非线性程度对算法性能的影响，构造功能函数：

分别计算k=2、3、4、5、6这5种情况下的可靠度指标，仍以100万次Monte Carlo直接抽样模拟的结果作为标准解，讨论变量服从正态分布的情况。

仍然假定正态分布的统计参数为式（14）。各情况可靠度指标计算结果见表2所示，各算法与标准解的比值见图2。

从上述图表中可以看出，当变量服从正态分布时，随功能函数非线性程度的提高：（1）重要抽样法与标准解吻合很好，且经验证，重要抽样法的抽样次数远小于直接抽样法；（2）当k为奇数时，JC法、响应面法、一次渐进法的精度较好均要优于k为偶数的情况，说明功能函数的奇偶性对算法精度有影响；（3）再次验证，非线性程度较低时，JC法与响应面法吻合较好，已经讨论；（4）非线性程度较高时，响应面法精度相对较低，这是因为将高度非线性功能函数近似成二次多项式的处理方式产生了较大的误差；（5）相比于线性功能函数时较低的精度，当非线性程度较高时，一次渐进法开始体现其优越性。

表2 不同非线性程度的可靠度指标

图2 不同非线性程度可靠度指标与标准解的比较

2.3 统计参数的影响

2.3.1 均值的影响

约定变量的变异系数：VR=[0.3;0.2]，分别在均值μ=kx[5;3]，k=1,2,3,4,5,6六种工况下计算结构可靠度指标。线性功能函数的形式为式（13），讨论变量服从正态分布的情况。上述6种情况下5种算法所得可靠度指标列于表3，精度对比见图3。

图表表明：（1）约定变异系数后，JC法、响应面法以及一次渐进法三种方法计算的可靠度指标并不随均值的改变而改变；这是因为变异系数不变时，变量的概率密度函数和累积分布函数不发生变化或变化较小；（2）图3是经放大处理后的效果，因此可以认为MC法和重要抽样法计算的可靠度指标发生变化是由抽样的不确定性引起的；（3）与非线性程度变化类似，随均值的变化，各算法精度变化同样具有区间性。

表3 不同均值的可靠度指标

图3 不同均值的可靠度指标与标准解比较

可以得出的结论是：在功能函数为线性，变量服从正态分布，且约定变异系数的情况下，各算法不受均值的影响或影响甚微。经验证，此结论可推广到非正态变量；同时，均值变化时，各算法精度同样具有区间性。

2.3.2 变异系数的影响

约定变量的均值μ=[25;10]，变异系数VR=[0.2;0.1]+k[0.1+0.05],k=1,2,3,4,5，共5种情况，计算结果如表4及图4所示。

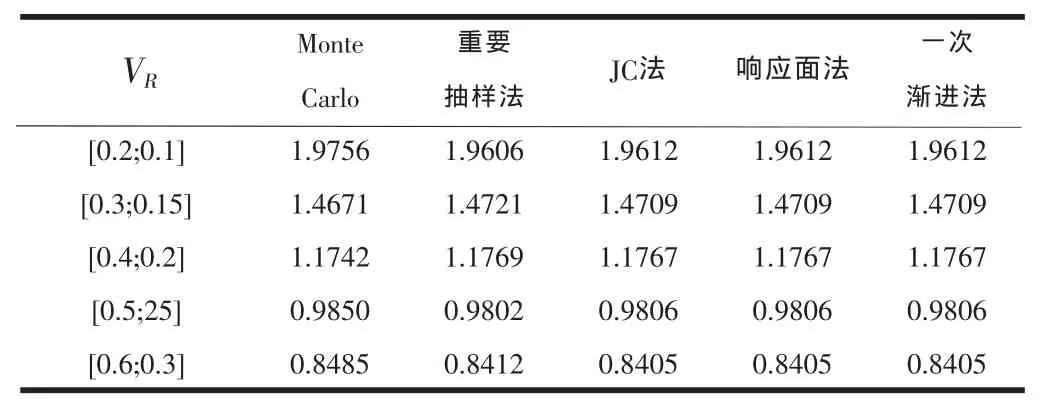
表4 不同变异系数的可靠度指标

图4 不同变异系数的可靠度指标与标准解的比较

（1）约定均值后，结构可靠度指标随变异系数的增加而递减，这是由变量的概率密度函数和累积分布函数决定的；（2）与均值变化相同，各算法精度随变异系数的变化也呈现出区间性。经验证，这两个结论同样可以推广到非正态分布和非线性功能函数的情况。

3 结论

从变量类型、非线性程度和统计参数三个方面着手，利用Matlab程序计算对比了五种常用的可靠度计算方法的性能，由计算结果可得出以下结论：

（1）随机变量类型对算法精度有影响，综合看来，Weibull分布对精度影响最大，对数正态分布其次，极值I型分布次之，正态分布变量精度最好；

（2）功能函数的奇偶性对算法精度有影响，算法精度随非线性程度的变化呈区间性变化；

（3）统计参数对算法精度影响较大，且也具有区间性；

（4）由于抽样的随机性直接抽样法与重要抽样法，每抽取的结果具有不定性，若选取的分布函数合适，重要抽样可以取得相当的精度，且可以提高计算效率；

（5）线性程度较低时响应面法与JC法吻合较好，但由于响应面法用二次多项式代替复杂的功能函数，故其随着非线性程度的提高，其精度相对最低；但在无法预先确定计算模型的情况下，响应面法具有优势；

（6）一次渐进法规避了当量正态化的过程，拟用最优化问题求解最大失效概率点。在非线性程度较高时，该法具有优势，但其计算程序较为复杂，且易受变量类型的影响，二次渐进积分法可解决此问题；

（7）可靠度计算方法受多方面因素的影响，选择计算方法时要综合考虑。

[1]李继华，林忠民，李明舜，等.建筑结构概率极限状态设计[M].北京：中国建筑工业出版社，1990.

[2]Shinozuka M.Basic analysis of structural safety[J].Journal of Structural Engineering，ASCE，1983，109（3）：721-740.

[3]Yaacob Ibrahim.Observations of applications of importance sampling in structural reliability analysis[J].Strucutural Safety，1991，10（4）： 269-281.

[4]丁幼亮，李爱群，邓洋，等.响应面在结构可靠度分析中的应用研究[J].东南大学学报，2011，28（2）：12-16.

[5]Breitung K.W.Asymptotic Approximations for Probability Integrals[M].Berlin：Springer-verlog，1994.

[6]Gayton N，Bourient J M，Lemaire M.CQ2RS： a New Statistical Approach to the Response Surface Method for Reliability Analysis[J].Structural Safety，2003，25（1）：99-121.

[7]Rubinstein R Y.Simulation and the Monte-Carlo Method[M].New York：Wiley，1981.

[8]Augusti G，Baratta A，Casciati F.Probabilistic Methods in Structural Engineering[M].London： Chapman and Hall，1984.

[9]Engeleund S，Rackwitz R A.Benchmark study on important sampling techniques in structural[J].Chinese Journal Safety，1993，12（4）： 255-276.

[10]赵国藩，金伟良，贡金鑫.结构可靠度理论[M].北京：中国建筑工业出版社，2000.

[11]Melchers R.E.Radial importance sampling for structural reliability[J].Journal of Engineering Mechanics，1990.116（1）：189-203.

[12]李云贵，赵国藩，张保和.结果可靠度的渐进分析方法[J].大连理工大学学报，1994，34（4）： 442-447.

[13]李远瑛，张德生.基于MATLAB的结构可靠度分析方法研究[J].嘉应学院学报，2011，29（2）：45-48.