铣刀磨损对铣削稳定性及表面位置误差的影响*

2015-01-12刘献礼宋盛罡哈尔滨理工大学机械动力工程学院哈尔滨150080

振动、测试与诊断 2015年4期

吴石，刘献礼，宋盛罡，渠达（哈尔滨理工大学机械动力工程学院哈尔滨，150080）

吴石，刘献礼，宋盛罡，渠达
（哈尔滨理工大学机械动力工程学院哈尔滨，150080）

为了分析刀具正常磨损后铣削颤振稳定域和表面位置误差，对刀具不同磨损状态下的切削力系数进行辨识，基于全离散法研究刀具正常磨损后铣削颤振稳定域和表面位置误差特性。发现当刀具正常磨损后，铣削系统的稳态临界切深呈现上升的趋势；随着工件表面洛氏硬度的提高，铣削系统稳态临界切深逐步下降，刀具正常磨损后临界切深与后刀面无磨损临界切深的差别逐步变小；在稳定域的局部会出现表面位置误差增加的情况。试验表明，该理论模型可以有效优化刀具正常磨损后的加工参数。

铣刀磨损；全离散法；稳定域；表面位置误差

引言

球头铣刀广泛应用于模具型腔表面及其他具有复杂成形表面的产品，是数控加工各种曲率变化或很陡曲面的重要刀具。从铣削稳定域预测、颤振控制和加工精度为目的的研究角度出发，在刀具出现磨损的情况下，准确地进行切削动态稳定性预测，防止刀具发生颤振，预防不稳定切削对模具加工精度和产品质量的影响。同时，高速铣削过程即使不发生颤振，加工过程磨损刀具的受迫振动也会影响工件的加工精度，主要影响表面位置误差（surface location error，简称SLE）［1］。

加工中刀具的动态磨损是影响加工精度的一个重要因素。刀具磨损产生的机理较复杂，影响因素较多，很难建立一个准确适用的刀具磨损理论模型，一般多基于试验方法进行研究［2-4］。李锡文等［5］基于后刀面磨损带面积建立螺旋立铣刀后刀面瞬时铣削力和平均铣削力数学模型，根据试验方法得到后刀面法向力系数和切向力系数来预测刀具不同磨损状态。张臣等［6］通过分析影响球头铣刀刀具磨损的几何加工参数，利用线性多因素回归法建立了球头刀具轴线磨损量模型和径向磨损量模型。文献［7-8］提取与刀具磨损量最相关的切削力和振动信号等作为等特征向量，然后基于隐性马尔可夫模型或超球面支持向量机进行刀具磨损状态识别。上述研究内容基本局限于磨损量的预测，所建立的刀具磨损模型大多是以在线监测刀具磨损状态为目的，而对球头铣刀磨损模型的建立、磨损后的切削稳定性以及刀具磨损产生的动态加工误差等研究较少。

笔者为研究刀具磨损情况下的切削稳定性及同步表面位置误差预测，以球头铣刀为研究对象，首先，利用切削力系数度量球头铣刀切削刃磨损量，基于正交切削辨识球头铣刀切削系数，分析切削力系数与刀具后刀面磨损量的相关性；然后，根据铣削过程动力学模型，基于全离散法预测多工艺参数耦合的稳定域边界和同步表面位置误差。目前，同步预测稳定域和表面位置误差的主要方法有时域有限元分析法［9-11］和全离散法。铣削过程稳定性分析中全离散法打破了经典微分方程框架，在积分方程框架下描述出了铣削过程动力学的时滞积分方程。全离散法是继时域有限元分析法后第2个能同步预报铣削稳定性与表面位置误差的半解析方法，与目前国际通用的半离散法相比，在保证数值精度的前提下，能够有效提高计算速度［12］。研究结果对高速铣削加工淬硬钢模具的推广应用具有理论和实际指导意义。

1 不同磨损阶段的铣削力系数

刀具的磨损形式主要包括前刀面磨损、后刀面磨损及边界磨损。研究表明，在切削时引起的刀具磨损主要是后刀面磨损。随着后刀面磨损带宽度的增加，作用在铣刀后刀面上的切削力因后刀面与工件间接触面积的增大而增大，而作用在铣刀前刀面上的切削力保持不变［13］。根据磨损曲线，可以将刀具磨损失效过程分为3个阶段：初始磨损、正常磨损及急剧磨损。假设新刀的后刀面磨损带量为零，轻微磨损的后刀面磨损量为26.86μm（大约切削10 min左右），刀具磨损的具体情况如图1所示。试验同型号刀具的后刀面磨损随时间变化情况如图2所示，后刀面磨损量为26.86μm时，刚刚进入正常磨损区间，根据刀具不同的磨损阶段，分别计算铣削力模型的系数，包括切向、径向、轴向剪切铣削力系数（Ktc，Krc，Kac）和切向、径向、轴向犁耕铣削力系数（Kte，Kre，Kae）。切削力系数根据Gradisek［14］方法进行铣槽试验，通过平均铣削力计算铣削力系数。

图1 刀具磨损的具体情况Fig.1 The specific situation of tool wear

图2 刀具后刀面磨损情况Fig.2 The wear situation of tool flank

在铣削力系数的测试过程中，机床为VDL-1000E型三轴立式加工中心，刀具为山特维克整体硬质合金球头立铣刀（R216.64-08030-AO09G 1610），直径为8 mm，螺旋角为30°的四刃硬质合金球头铣刀，工件材料为不同洛氏硬度的淬硬钢（59 HRC，49 HRC，45 HRC）。针对不同硬度材料、新刀、轻微磨损刀具，这6种情况分别采用相同切削参数进行铣槽试验，即轴向切削深度分别为0.1，0.2，0.3，0.4 mm，进给速度分别为500，1 000，1 500 mm/min，转速为4 000 r/min。平面干切削每种情况共进行12组试验，每组试验重复3次取平均值得到平均铣削力。测力仪型号为Kistler9257B，传感器选用PCB加度传感器，灵敏度为10.42 m V/g，电荷放大器型号为Kistler5007；数据采集分析系统采用东华DH5922信号采集系统，切削力测试系统如图3所示。传感器布置和模态测试如图4所示。铣削系统模态特性通过锤击试验获得，如表1所示。铣削力系数如表2所示。

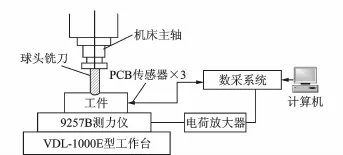
图3 铣削力系数测量系统Fig.3 Measurement system for milling force coefficient

图4 传感器的布置和模态测试图Fig.4 The specific layout of sensors and modal test

表1 球头铣刀的模态特性Tab.1 Modal characteristics of ball-end milling cutter

2 基于全离散法的颤振稳定域预测

切削过程颤振分为再生型颤振和模态耦合型颤振，一般认为再生型颤振先于模态耦合型颤振发生。笔者基于全离散法来预报铣削稳定性和表面位置误差。具有对称动力学参数的两自由度铣削动力学模型［15］为

表2 球头铣刀铣削力系数Tab.2 Milling force coefficients of ball-end milling cutter

其中：mt为铣削系统的模态质量；ζ为铣削系统的阻尼比；ωn为铣削系统的固有频率；ap为轴向铣削深度；hij（t）为时变铣削力系数；i，j=1，2。

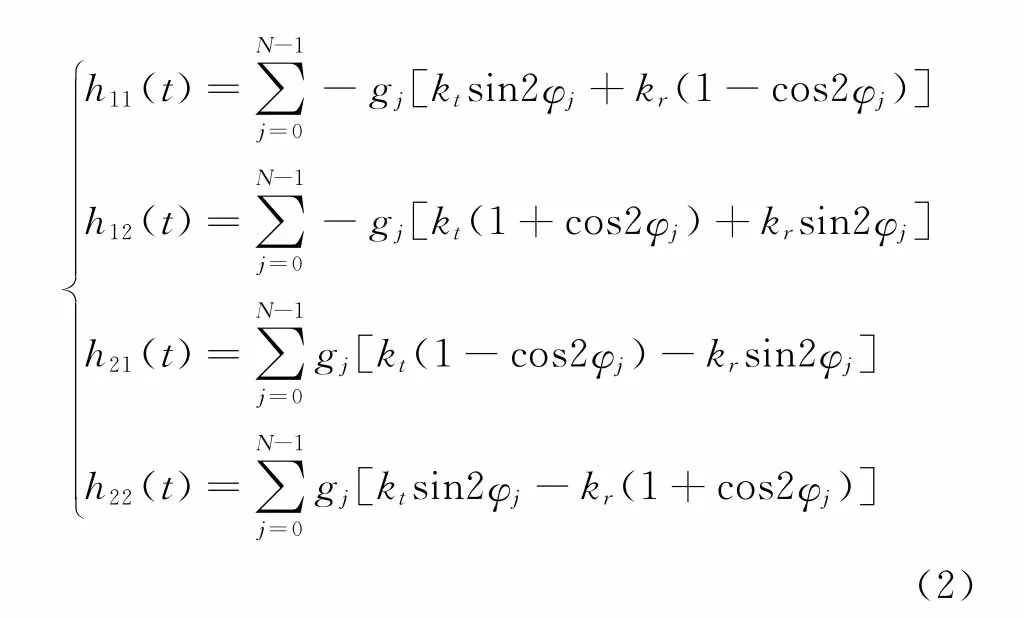
其中：φj（t）为刀齿j的位置角度；φj=ωt+j（2π/N），j=0，1，2，…，N-1；N为铣刀齿数；kt为切向铣削力系数；kr为径向铣削力系数；gj为刀齿的有效切削区函数。

将质量矩阵、阻尼系数矩阵和刚度矩阵分别表示为M，C和K，并设［x（t），y（t）］T=q（t），p（t）= M˙q+C q/2，R（t）=［q（t），p（t）］T，通过柯西变换，两自由度铣削动力学模型的状态空间形式［16-17］为

其中间T等距离离散为m个时间段，即T=mτ。根据精细积分法［18-19］，通过线形逼近和根据Floquet理论，求得系统的稳定性可由转移矩阵的特征值决定。若转移矩阵的所有特征值的模均小于1，则系统稳定［19］。具体研究步骤根据单自由度铣削动力学模型进行［17］。

根据球头铣刀后刀面磨损情况不同，铣削力系数不同，分别建立铣削系统颤振二维稳定域图，如图5，6所示。从图5看出，后刀具面轻微磨损时，对于工件不同的表面洛氏硬度（45，49，59HRC）铣削系统的稳态临界切深呈现上升的趋势；在主轴高转速的区域，后刀具面轻微磨损的稳态临界切深较后刀面无磨损的稳态临界切深要大的多；洛氏硬度为59 HRC时，刀具轻微磨损对稳定域影响较小；洛氏硬度为45，49HRC时，刀具轻微磨损对稳定域影响较大。从图6可以看出，随着工件表面硬度的提高，铣削系统稳态临界切深逐步下降，刀具轻微磨损后临界切深与后刀面无磨损临界切深的差别逐步变小；切削在不同硬度工件时，后刀面如果无磨损在6.5～7.0 kr/min间有hof分叉叶瓣。

3 基于全离散法的动态加工误差同步预报

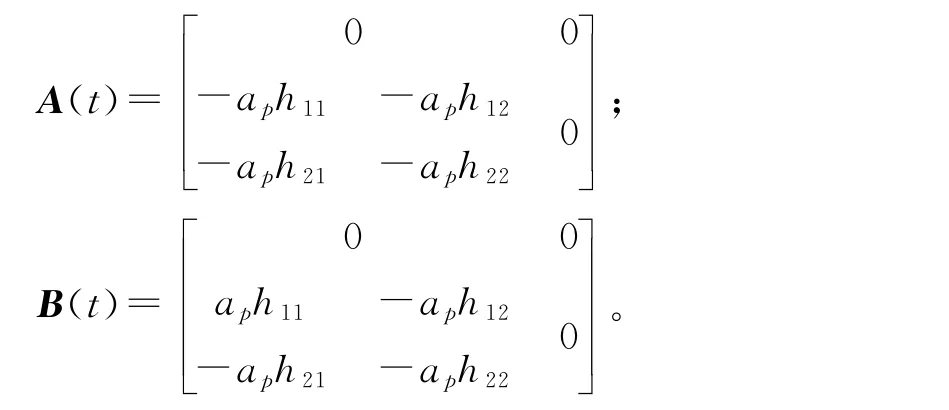
将刀具一转的时间T等同于时滞量，将时滞时在考虑铣削系统颤振稳定域同时，应同时考虑在稳定域内铣削的表面位置误差，即铣削系统颤振稳定域和表面位置误差同步预报。计算表面位置误差，即考虑振动诱导的动态加工误差［20］，需要考虑动力学方程的静态项，即

图5 考虑后刀面磨损程度时铣削系统颤振二维稳定域Fig.5 The chatter stability of milling system by considering the degree of tool flank wear

图6 考虑铣削不同硬度工件时铣削系统颤振二维稳定域Fig.6 The chatter stability of milling system by considering the different hardness of workpiece

其中：为进给率。

将刀具一转的时间T等同于时滞量，将时滞时间T等距离离散为m个时间段，即T=mτ，τ为采样周期，m为正整数，通过线形逼近可得如下离散［17］形式

若［I-Fk+1］-1奇异，则可用该矩阵的广义逆代替对其求逆。使用扩展的状态向量yk=col（xk，xk+1，…，xk+1-m，xk-m），yk为n（m+1）维向量，构造如下离散映射

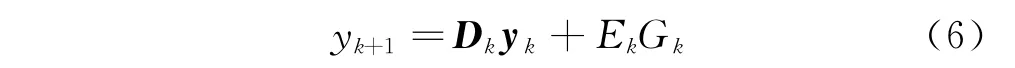
其中：Dk=

系统在单个时间周期上的状态转移矩阵关系可以通过矩阵序列Dk，Ek，Gk，（k=0，1，…，m-1）构造出来，即

对于多周期情况，第l周期和第l-1周期的离散动态映射可从式（6）得到，即

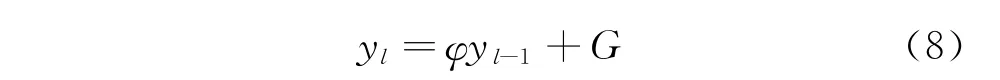
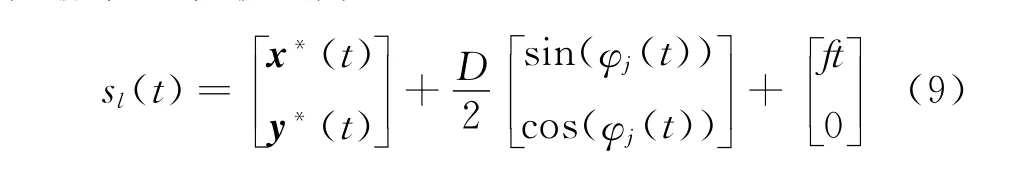
表面位置误差表示为

当表面洛氏硬度为59 HRC，轴向切深ap= 0.6 mm时，根据后刀面有无轻微磨损（其切削力系数不同），预报表面位置误差，如图7所示。可以看出，刀具轻微磨损后低转速的动态误差几乎为零，只是在高转速是动态误差增长的较快。从图7（a）可以看出，在刀具无磨损时，转速在6.0，7.8，9.5 kr/min等附近出现表面位置误差急剧增加的趋势。从图7（b）可以看出，在转速为9.5 kr/min时，表面位置误差开始急剧变化。

图7 考虑后刀面磨损程度时表面位置误差预报Fig.7 The surface location error prediction by considering the degree of tool flank wear

4 试验及分析

由于刀具转速和切深是影响铣削稳定性的两个较主要数据，通过测试系统在不同工艺参数下获得工件振动加速度信号，采样频率为10 k Hz。工件表面洛氏硬度为45HRC时，共进行12组试验，每组采用两种刀具，一种后刀面有轻微磨损（开始测试时后刀面磨损量为26.86μm）和一种后刀面无磨损，转速分别为3.5，4.0，4.5，5.0，5.5，6.0 kr/min，切深ap分别为0.4，0.6 mm，每齿进给量为0.15 mm。

如图8所示，当转速为4 kr/min、切深为0.4 mm时，转速在5 kr/min、切深为0.4，0.6 mm时，工件振动较小，振幅为5 mm/s2左右。如图8（c）所示，该工况下铣削稳定无颤振，工件表面质量较好。通过傅里叶变换发现能量在刀具转动频率附近，能量分布均匀。

图8 铣削颤振稳定域的试验分析Fig.8 The experiment analysis of milling chatter stability

当转速在3.5，4.5，5.5，6.0 kr/min，切深为0.6 mm时，工件出现明显振动，最大振幅达到16.7 mm/s2左右，如图8（b）所示，该工况下铣削不稳定有颤振，工件表面质量较差。通过傅里叶变换发现能量向刀具结构频率附近积聚，且能量增大很多。当转速在3.5，4.0，4.5，5.5，6.0 kr/min，切深为0.4 mm时，工件出现轻微颤振，最大振幅为12.6，14.6 mm/s2左右，刀具无磨损的时域振动信号如图8（d）所示。刀具轻微磨损的时域振动信号分析如图8（e）所示，刀具轻微磨损的时域振动信号略大。当后刀面有轻微磨损，转速在4.0，6.5 kr/min，切深ap=0.4 mm时，工件表面的质量如图9所示，符合预测的规律。根据刀具正常磨损后铣削颤振稳定域和表面位置误差模型，可以初步优化刀具正常磨损后的加工参数。

图9 稳定域内工件表面（切深ap=0.4 mm）Fig.9 The workpiece surface in the stability region（The depth of cut ap=0.4 mm）

5 结论

1）不同磨损状态下的切削力系数不同；刀具后刀面轻微磨损后，铣削系统的稳态临界切深呈现上升的趋势；随着工件表面硬度的提高，铣削系统稳态临界切深逐步下降，刀具轻微磨损后临界切深与后刀面无磨损临界切深的差别逐步变小。

2）在局部稳定域会出现表面位置误差增加的情况，刀具轻微磨损后，低转速的动态误差几乎为零，只是在高转速时表面位置误差增长较快；表面位置误差的产生使稳定切削的振动加大，铣削质量下降。

3）全离散法的特点是具有较高的计算效率，可以据此很好地研究刀具磨损后铣削颤振稳定域和表面位置误差特性；铣削稳定域的研究和表面位置误差预报相结合可以有效优化加工工艺。

［1］ Schmitz T，Ziegert J.Examination of surface location error due to phasing of cutter vibrations［J］.Precision Engineering，1999，23：51-62.

［2］ Koshy P，Dumitresci P，Ziada Y.Novel methods for rapid assessment of tool performance in milling［J］.Institution Journal of Machine Tools and Manufacture，2004，44（5）：1599-1605.

［3］ Wang W H，Hong G S，Wang Y S.Flank wear measurement by a threshold independent method with subpixel accuracy［J］.International Journal of Machine Tools and Manufacture，2006，46（2）：199-207.

［4］张辉，陈五一.基于初期磨损统计规律的铣刀快速筛选［J］.机械工程学报，2011，47（11）：191-198.Zhang Hui，Chen Wuyi.Milling tool rapid selection based on statistical law of initial wear［J］.Journal of Mechanical Engineering，2011，47（11）：191-198.（in Chinese）

［5］李锡文，杜润生，杨叔子.基于后刀面磨损带面积的铣刀磨损模型的建立［J］.华中科技大学学报，2001，29（4）：53-56.Li Xiwen，Du Runsheng，Yang Shuzi.Tool wear modeling based on the area of the major flank wear land［J］.Journal of Huazhong University of Science and Technology，2001，29（4）：53-56.（in Chinese）

［6］张臣，周来水，安鲁陵，等.球头铣刀刀具磨损建模与误差补偿［J］.机械工程学报，2008，44（2）：207-212.Zhang Chen，Zhou Laishui，An Luling，et a1.Modeling and wear-induced error compensation of ball-end milling cutter wear［J］.Journal of Mechanical Engineering，2008，44（2）：207-212.（in Chinese）

［7］康晶，冯长建，胡红英.刀具磨损监测及破损模式的识别［J］.振动、测试与诊断，2009，29（1）：5-9.Kang Jing，Feng Changjian，Hu Hongying.Tool wear monitoring and pattern recognition of tool failure［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2009，29（1）：5-9.（in Chinese）

［8］刘路，王太勇，蒋永翔，等.基于超球面支持向量机的刀具磨损状态识别［J］.农业机械学报，2011，42（1）：218-222.Liu Lu，Wang Taiyong，Jiang Yongxiang，et a1.Tool wear state recognition based on hyper-sphere support vector machin［J］.Transactions of the Chinese Society for Agricultural Machinery，2011，42（1）：218-222.（in Chinese）

［9］ Insperger T，Gradisek J，Kalveram M，et al.Machine tool chatter and surface location error in milling processes［J］.Journal of Manufacturing Science and Engineering，2006，128（4）：913-920.

［10］Bachrathy D，Insperger T，Stepan G.Surface properties of the machined workpiece for helical mills［J］.Machining Science and Technology，2009，13：227-245.

［11］Ding Ye，Zhu Limin，Zhang Xiaojian.On a numerical method for simultaneous prediction of stability and surface location error in low radial immersion milling ［J］.Journal of Dynamic Systems，Measurement and Control，2011，133（3）：5031-5038.

［12］Ding Ye，Zhu Limin，Zhang Xiaojian，et al.A fulldiscretization method for prediction of milling stability ［J］.International Journal of Machine Tools and Manufacture，2010，50（5）：502-509.

［13］Bayyoumi A E，Yucesan G，Kendall L A.An analytic mechanistic cutting force model for milling operations：a theory and methodology［J］.ASME Transactions，Journal of Engineering for Industry，1994，116（8）：324-330.

［14］Gradisek J，Kalveram M，Weinert K.Mechanistic identification of speeific force coefficients for a general end mill［J］.International Journal for Numerical Methods in Engineering，2004，44（4）：401-414.

［15］Gradisek J，Kalveram M，Insperger T，et al.On stability prediction for milling［J］.International Journal of Machine Tools and Manufacture，2005，45（7/8）：769-781.

［16］Insperger T，Stepan G.Updated semi-discretization method for periodic delay-differential equations with discrete delay［J］.International Journal of Machine Tools and Manufacture，2004，61（1）：117-141.

［17］丁烨.铣削动力学——稳定性分析方法与应用［D］.上海：上海交通大学，2011：23-26.

［18］Tan Shujun，Zhong Wanxie.Precise integration method for duhamel terms arising fromnon-homogenous dynamic systems［J］.Chinese Journal of Theoretical and Applied Mechanics，2007，39（3）：374-381.

［19］Zhong Wanxie，Williams F W.A precise time step integration method［J］.Proceedings of the Institution of Mechanical Engineers，Part C，Mechanical Engineering Science，1994，208（6）：427-430.

［20］Mann B P，Edes B T，Easley S J，et al.Chatter vibration and surface location error prediction for helical end mills［J］.International Journal of Machine Tools and Manufacture，2008，48（3-4）：350-361.

［21］Insperger T，Gradisek J，Kalveram M，et a1.Machine tool chatter and surface location error in milling processes［J］.Journal of Manufacturing Science and Engineering，2006，128（4）：913-920.