基于切削声信号与优化SVM的刀具磨损状态监测*

2015-01-12张锴锋,袁惠群,聂鹏

振动、测试与诊断 2015年4期

张锴锋1，2，袁惠群1，聂鹏2

（1.东北大学机械工程与自动化学院沈阳，110819）（2.沈阳航空航天大学机电工程学院沈阳，110136）

提出了一种利用切削声实现刀具磨损状态多特征监测的方法。根据经验模态分解与Hilbert变换理论，提取切削声信号的内禀模态能量与不同频段的Hilbert谱能量作为监测信号的备选特征。采用支持向量机作为分类器，针对备选特征的有效筛选问题，利用多种群遗传算法对分类器的输入特征进行了优化，剔除备选特征中的干扰特征，利用多种群遗传算法对分类器的模型参数进行了优化。利用优化后的分类器对测试样本进行分类，并与优化前的分类结果进行了对比。结果表明，优化后分类器的分类性能得到了明显提升，该方法可以对刀具磨损状态进行有效识别。

经验模态分解；Hilbert变换；切削声；支持向量机；多种群遗传算法

引言

金属切削过程中，随着刀具磨损量的增加，可以听到切削的声音会发生相应的变化，这说明可听阈范围内存在着可用于刀具磨损状态识别的信息。当刀具逐渐磨损时，刀具与工件之间的摩擦力会随着接触面的增加而增大，而由摩擦力和剪切力引起的刀具与工件的振动是切削声信号产生的主要来源［1］，切削声音信号与刀具磨损量存在明显的相关

性。此外，用于声信号采集的传声器具有安装方便、成本低和灵敏度高等特点，因此利用切削声信号实现对刀具磨损状态的监测具有很好的应用前景，并且在刀具状态监测领域的研究中得到了应用。文献［2］利用切削声信号的时域和频域分析方法，对钻削时刀具磨损的监测方法进行了研究。文献［3-4］利用切削声信号的线性预测倒谱系数（linear predictive cepstrum coefficient，简称LPCC）对铣削刀具磨损监测进行了研究。文献［5］以切削力以及切削声信号的奇异谱为监测特征，利用最小二乘支持向量机实现车削刀具磨损状态的在线监测。由于切削声信号的频率较低，容易受到其他噪声的影响，因此如何从采集到的信号中提取并筛选出有效的切削声信号特征，是声音监测法研究的重要环节。

笔者利用经验模态分解（empirical mode decomposition，简称EMD）和Hilbert变换方法，对可听阈频率范围（20 Hz～20 k Hz）内的车削加工声信号进行分解与滤波，提取内禀模态能量与不同频段的Hilbert谱能量作为刀具状态监测信号的备选特征。由于经EMD滤波后的声信号中仍存在噪声干扰信号，且不同的信号特征与刀具磨损量的相关程度也存在差异，因此并不是所有的备选特征都是有用特征，无用的干扰特征的存在反而会影响识别结果的准确性。笔者采用特征筛选与分类器训练相结合的方法，利用多种群遗传算法对支持向量机（support vector machine，简称SVM）的输入特征进行筛选，特征筛选后再次利用多种群遗传算法对SVM模型参数进行优化，并利用优化后的SVM对刀具磨损状态进行识别。

1 基于EMD的信号滤波与特征提取方法

EMD是一种高效的自适应信号处理方法，该方法基于信号的局部特征时间尺度，将复杂的数据组分解成为数量有限且通常很少的内禀模态函数（intrinsic mode function，简称IMF），适合处理非线性、非平稳信号［6］。EMD方法对信号x（t）的分解可以表示为

其中：ci（t）（i=1，2，…，n）为IMF分量；rn（t）为残差，代表信号的平均趋势。

对实验采集到的声信号进行频谱分析，在机床空转工况下，声信号的频谱如图1所示。将此时采集到的声信号视为噪声信号，可见噪声信号主要存在于2kHz以下的低频范围。

图1 空转工况下声信号频谱Fig.1 Thespectrumofsoundsignalinidlingcondition

对车削加工过程中采集到的声信号进行EMD分解，得到的各IMF分量包含了信号从高到低不同的频率成份，合理的选择IMF分量从原始信号中排除，可以实现对声信号的滤波。研究发现，将低频IMF分量从原始信号中排除，仅保留前4个IMF分量（如图2所示），可以对低频噪声信号起到抑制作用。滤波前后的切削声信号频谱分别如图3，4所示。

图2 切削声信号与前4个IMF分量Fig.2 ThefirstfourIMFcomponentsofcuttingsound signal

图3 EMD滤波前切削声信号频谱Fig.3 Thespectrumofcuttingsoundsignalbefore EMDfiltering

图4 EMD滤波后切削声信号频谱Fig.4 ThespectrumofcuttingsoundsignalafterEMD filtering

分别提取保留的各IMF分量的能量值，计算公式为

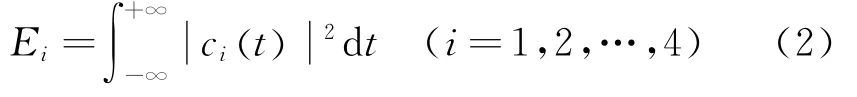
随着刀具磨损量的增加，各IMF分量能量值会发生相应的变化，因此将该能量值作为声信号的备选监测特征。

2 基于Hilbert变换的特征提取方法

信号经过EMD分解后，其瞬时频率具有了物理意义，对内禀模态函数进行Hilbert变换，求出瞬时频率随时间变化的函数，并最终得到信号幅值随频率和时间的分布H（ω，t），该分布称为Hilbert谱，其表达式为

由Hilbert边际能量谱可以得到信号的Hilbert谱对应不同频段的能量特征Si，其计算公式为

定义Hilbert边际能量谱其中：ωi，ωi+1分别为频段的上、下边界频率；n为划分的频段数。

由于Hilbert谱体现了信号瞬时频率的物理意义，不同刀具磨损状态下提取的能量特征Si能够更精确地反应信号能量随频率和时间的变化情况，因此将Si作为声信号的备选监测特征。

3 多种群遗传算法优化SVM

3.1 SVM理论

SVM的基本思路是寻找最优分类超平面，并把该寻优问题归结为求解一个凸二次规划问题。对于线性可分问题，分类超平面使分类间隙最大；对于非线性分类问题，通过非线性映射Φ，将输入空间的样本映射到高维的特征空间［9］，使非线性分类问题转化为高维特征空间的线性可分问题。为了解决升维带来的复杂的计算问题和避免“维数灾难”，引入满足Mercer条件的核函数K来替代高维特征空间中的点积运算。假定二类别分类问题n个样本的训练集为D=｛（xi，yi）（i=1，2，…，n｝，xi∈Rn，则高维特征空间分类超平面可定义为

其中：w为法向向量；b为常数。

最优分类超平面的寻优问题可转化为对偶二次规划问题［10］

其中：K（xi，xj）=（Φ（xi），Φ（xj））；αi为拉格朗日乘子；C为惩罚因子。得到的最优分类函数为

基本的SVM只能解决二类别分类问题，对于多分类问题需要通过一定的算法对多个基本的SVM进行组合。由于“一对一”算法比较适合实际应用［12］，因此采用该算法解决多分类问题。

3.2 多种群遗传优化方法

遗传算法是一种建立在自然选择和遗传学基础上的搜索寻优算法，原始的遗传算法（simple genetic algorithm，简称SGA）在个体适应度差异、算法参数选择、种群规模和遗传代数等因素的影响下，容易出现未成熟收敛的现象，因此笔者采用了改进的遗传算法，即多种群遗传算法（multiple population genetic algorithm，简称MPGA）。MPGA在SGA的基础上引入了多种群协同进化的概念，各种群之间通过移民算子交换各自的最优个体，并通过人工选择算子将各种群每一代进化的最优个体放入精华种群加以保存，以精华种群最优个体的保持代数作为优化终止判据，取代了SGA以人为设置最大遗传代数为终止判据的方法。此外，MPGA中各种群选取不同的交叉概率和变异概率，通过协同进化，增强了算法的全局和局部搜索能力。

由于经EMD滤波后的声信号中仍存在噪声干扰信号，且不同的信号特征与刀具磨损量的相关程度也存在差异，因此并不是所有的备选特征都是有用特征，无用的干扰特征的存在反而会影响识别结果的准确性，而惩罚因子C和核函数参数γ对SVM的性能有很大影响。笔者采用MPGA对SVM进行优化，包括输入特征的筛选和模型参数的优化。输入特征的筛选方法为：将种群中个体（即染色体）的基因个数设置为与备选特征值的个数相等，并建立一一对应关系；基因采用二进制编码，“1”对应选中的有用特征，“0”对应排除的干扰特征；选取SVM的预测正确率为目标函数，对应目标函数较大的个体获得较大的适应度值参与进化，经过多次进化筛选出最终作为SVM输入的特征值。模型参数的优化方法为：以筛选得到的特征值为SVM的输入，以采用径向基函数作为SVM的核函数，其在一些信号特征分类的应用中具有良好的性能［11］，表达式为SVM的惩罚因子C和核函数参数γ为优化对象，对其进行编码形成种群；同样以SVM的预测正确率为目标函数，对应目标函数较大的个体获得较大的适应度值参与进化，经过多次进化，最终找到最优的个体，对其进行解码，完成SVM模型参数的寻优过程。

4 实验分析

通过实验对刀具磨损监测方法进行验证与分析，实验流程如图5所示。

图5 实验流程Fig.5 Experimental procedures

4.1 信号采集

信号采集在车床CA6161A上进行，刀片材料为涂层硬质合金YBG205（M20-M40），工件材料为高温合金GH2135。声信号采集采用杭州爱华的AWA14423型传声器和AWA14603型前置放大器，仪器测量频率为10～20 000 Hz，信号采样频率设置为64 k Hz。传声器贴近且正对切削区域安放，与刀具进给保持同步，如图6所示。

图6 切削声信号的采集Fig.6 Collect cutting sound signal

选择的3组切削参数如表1所示。每组切削参数下分别采集60组（共计180组）对应不同刀具磨损状态的数据，每组数据包含4 096个采样点，如图7所示（以第1组切削参数为例），并测量刀片磨损VB值。设置磨损区间：初期磨损（VB值小于0.2 mm），中期磨损（VB值在0.2～0.3 mm之间），后期磨损（VB值大于0.3 mm）。

表1 切削参数Tab.1 Cutting parameters

图7 采集到的切削声信号Fig.7 The collected cutting sound signal

4.2 特征值提取

由于信号采样频率为64 k Hz，根据采样定理，理论上能采集到的信号的最高频率为32 k Hz，因此在特征提取前，首先对采集到的各组信号进行低通滤波（截止频率为20 k Hz），使得信号的频率在研究的可听阈范围内。对低通滤波后的信号进行EMD分解，并利用式（2）提取前4个IMF分量的能量特征Ei（i=1，2，…，4）；对EMD滤波后的信号（即前4 个IMF分量）进行Hilbert变换，得到其Hilbert谱H（ω，t），在2～20 k Hz频率范围内每隔1 k Hz设置一个频段，并利用式（5），（6）提取Hilbert谱对应不同频段的能量特征Si（i=1，2，…，18）。以上提取的特征值结合切削参数（主轴转速n，切削深度ap，进给量f）组成的特征向量可表示为（E1，E2，…，E4，S1，S2，…，S18，n，ap，f），共包含25个特征值。将180组数据计算得到的180个特征向量分为3组（每组均包含不同磨损阶段特征向量），并进行归一化处理，得到SVM的备选输入特征样本。第1组包含45个样本，用于SVM的训练；第2组包含45个样本，用于SVM在优化的过程中计算目标函数；第3组为测试集，包含90个样本，用于验证优化后SVM的性能。

4.3 SVM优化与状态识别

采用MPGA对SVM进行优化，MPGA的相关参数设置如表2所示。

表2 MPGA参数设置Tab.2 The parameters of MPGA

在输入特征的筛选过程中，MPGA各种群个体的基因数量设置为25（与备选输入特征数量相同），SVM模型参数根据经验初选为C=2，γ=1。经过多次筛选研究发现，由于初始种群为随机选取，每次进化的最终结果存在一定的偏差，因此笔者采用多次筛选后提取选中概率较大特征值作为最终优化结果的方法。经过20次筛选，提取出选中概率大于70％的特征值共19个，作为SVM的输入特征，按序以向量的形式表示为（E1，E3，E4，S1，S2，S3，S4，S6，S7，S8，S10，S11，S12，S13，S14，S15，n，ap，f）。图8为刀具磨损3个不同阶段分别筛选出的特征值，其中后3个特征值为切削参数归一化特征值。最终的筛选结果包含切削参数特征，说明多工况下的刀具磨损状态识别中切削参数特征是十分必要的。此外，虽然单次筛选出的特征值一般也能使SVM在训练时获得较高的分类准确率，但经研究发现，与多次筛选方法相比，SVM的泛化能力要有所降低。选中概率标准值设置为70％是通过试验的方法得出，过小的标准值无法起到筛选的作用，分类器的性能没有提升；而标准值过大时，筛选出的特征值过少，分类器的准确性和泛化能力也会下降。

以上述19个特征值作为SVM的输入特征，对SVM的惩罚因子C和核函数参数（进行优化，两个参数的寻优范围分别设置为0＜C≤50和0≤γ≤50，MPGA各种群个体的基因数量设置为10。图9 为SVM模型参数的寻优过程，经过15代进化，目标函数值由90提升到97.8，最终确定的寻优结果为C=0.977，γ=1.564。

图8 三组切削参数下筛选出的特征值Fig.8 The selected features for three groups of cutting parameters

利用优化后的SVM对90组测试样本进行分类，预测准确率为88.89％；而未经优化的SVM（即利用全部25个特征值为输入特征，模型参数根据经验设置为C=2，γ=1），预测准确率为85.56％。预测结果表明，通过MPGA的优化，SVM的分类准确率得到了提高。SVM优化后仍存在没有正确识别的样本，分析其原因发现，多数误判样本位于磨损期的过渡阶段，由于该类样本的特征与两个磨损区间的训练样本特征都比较接近，因此容易出现误判。此外，切削过程中的不稳定因素也会引起个别信号样本的特征值与训练样本差别过大，从而造成误判。

图9 参数寻优过程Fig.9 The process of parameters optimization

5 结束语

采用切削声信号作为刀具磨损监测信号，根据经验模态分解与Hilbert变换理论对信号进行特征提取，采用SVM作为分类器，并利用多种群遗传算法对分类器的输入和模型参数进行优化。对实测信号的分析结果表明：通过选择合适的特征提取方法，切削声信号可以用于刀具磨损状态的有效识别；可听阈范围内的切削声信号中可以提取出用于刀具磨损监测的有效特征；特征筛选与分类器训练相结合，可以有效剔除备选特征中的干扰特征，更有利于分类器性能的发挥；利用多种群遗传算法对SVM进行优化，能够使SVM的分类性能得到提高。

［1］ Trabelsi H，Kannatey-Asibu Jr E.Pattern-recognition analysis of sound radiation in metal cutting［J］.International Journal of Advanced Manufacturing Technology，1991，6：220-231.

［2］ Rafezi H，Behzad M，Akbari J.Time domain and frequency spectrum analysis of sound signal for drill wear detection［J］.International Journal of Computer and Electrical Engineering，2012，4（5）：722-725.

［3］ Ai C S，Sun Y J，He G W，et al.The milling tool wear monitoring using the acoustic spectrum［J］.International Journal of Advanced Manufacturing Technology，2012，61：457-463.

［4］艾长胜，何光伟，董全成，等.铣削声谱LPCC与刀具切削时间的关系［J］.振动、测试与诊断，2010，30（3）：264-268.Ai Changsheng，He Guangwei，Dong Quancheng，et al.Relationship between linear predictive cepstrum coefficient of milling sound and cutting time［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2010，30（3）：264-268.（in Chinese）

［5］ Salgado D R，Alonso F J.An approach based on current and sound signals for in-process tool wear monitoring［J］.International Journal of Machine Tools and Manufacture，2007，47（14）：2140-2152.

［6］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society A，1998，454：903-995.

［7］李辉，郑海起，唐力伟.瞬时频率估计的齿轮箱升降速信号阶次跟踪［J］.振动、测试与诊断，2007，27（2）：125-128.Li Hui，Zheng Haiqi，Tang Liwei.Order tracking of speed-up signal for gearbox based on instantaneous frequency estimation［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2007，27（2）：125-128.（in Chinese）

［8］于德介，程军圣，杨宇.Hilbert-Huang变换在齿轮故障诊断中的应用［J］.机械工程学报，2005，41（6）：102-107.Yu Dejie，Cheng Junsheng，Yang Yu.Application of Hilbert-Huang transform method to gear fault diagnosis［J］.Chinese Journal of Mechanical Engineering，2005，41（6）：102-107.（in Chinese）

［9］刘永斌，何清波，孔凡让，等.基于PCA和SVM的内燃机故障诊断［J］.振动、测试与诊断，2012，32（2）：250-255.Liu Yongbin，He Qingbo，Kong fanrang，et al.Fault diagnosis of internal combustion engine using PCA and SVM［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2012，32（2）：250-255.（in Chinese）

［10］吴德会.一种基于支持向量机的齿轮箱故障诊断方法［J］.振动、测试与诊断，2008，28（4）：338-342.Wu Dehui.Gearbox fault diagnosis based on SVM［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2008，28（4）：338-342.（in Chinese）

［11］Elangovan M，Sugumaran V，Ramachandran K I，et al.Effect of SVM kernel functions on classification of vibration signals of a single point cutting tool［J］.Expert Systems with Applications，2011，38：15202-15207.

［12］Hsu C W，Lin C J.A comparison of methods for multiclass support vector machines［J］.IEEE Transactions on Neural Networks，2002，13（2）：415-425.