机械臂反演非奇异终端的神经滑模控制*

贾育秦，胡晓雄（1.吕梁学院矿业系 吕梁，033001）（.太原科技大学机械工程学院 太原，03004）

机械臂反演非奇异终端的神经滑模控制*

贾育秦1，2，胡晓雄2
（1.吕梁学院矿业系 吕梁，033001）（2.太原科技大学机械工程学院 太原，030024）

为了解决具有外部干扰以及建模误差的多关节机械臂的轨迹跟踪问题，提出了一种机械臂反演非奇异终端的神经滑模控制方法。采用非奇异终端的滑模面，基于反演方法以及滑模控制的原理，设计了反演滑模控制器。针对由于外部干扰以及建模误差引起的反演滑模控制系统中不确定的因素上界，设计了径向基（radial basis function，简称RBF）神经网络的自适应律，对不确定因素上界进行了在线估计，并对控制系统的稳定性使用了Lyapunov定理进行证明。仿真分析结果表明，所提出的方法不仅可以减少系统中存在的抖振现象，而且具有较好的轨迹跟踪性能和较强的鲁棒性。

反演控制；神经网络；滑模控制；非奇异终端

引 言

滑模变结构控制在实际的控制系统中应用十分广泛，尤其在不确定的非线性系统的控制中占有重要地位，原因是其对某一类的参数变化与有界的干扰具有相当强的鲁棒性，且被控对象不需要具有精确的数学模型［1-3］。反演设计的方法对具有参数的严格反馈形式的非线性系统给予了递推的步骤，使控制系统全局的稳定性有了保证［4］。终端滑模控制使控制系统拥有有限时间收敛的优点，然而当控制系统的状态逼近0时，对于存在于控制律中的状态负指数，其将使得控制量接近于无穷大，造成奇异点［5］。因此，设计了非奇异终端的滑模控制［6-9］。文献［10］对空间机器人的软硬性抓取使用滑模控制进行了分析。文献［11］为了提高对外部干扰的鲁棒性以及机械臂的跟踪性能，针对电动机驱动的机械臂设计了积分反演滑模控制。文献［12］对参数不确定的柔性机械臂设计了神经滑模控制。文献［13］为了使非奇异终端的滑模控制的局限性有所改善，使用模糊控制调节的滑模控制的切换增益。文献［14］对机械臂的轨迹跟踪设计了滑模控制。以上控制方法都得到了比较好的控制精度和动态性能。

笔者将滑模控制、反演控制以及神经网络进行结合，提出了反演非奇异终端的神经滑模控制方法。该方法汲取了反演控制以及滑模控制的优点，并且设计了RBF神经网络的自适应控制器，从而实现对外部干扰以及建模误差的自动跟踪，削弱了控制系统中存在的抖振现象，并使用Lyapunov定理对系统的稳定性进行证明。

1 建立系统模型

图1为2关节的机械臂示意图。其中：q1与q2为机械臂L1，L2旋转的角度；机械臂L2可以围绕O2（关节点）旋转；机械臂L1可以围绕O1（关节点）旋转。

对具有2个旋转关节点的刚性机械臂进行分析，其动力学方程为

其中：u为控制力矩；ρ（t）为外部的干扰与建模的误差；d（t）为外部的干扰；ΔM（q），ΔC（q，˙q）˙q，ΔG（q）为建模误差。

q（关节角的位置矢量）能够非常好地跟踪qd（指定的关节角位置矢量）是机械臂轨迹跟踪的控制目标的主要要求。

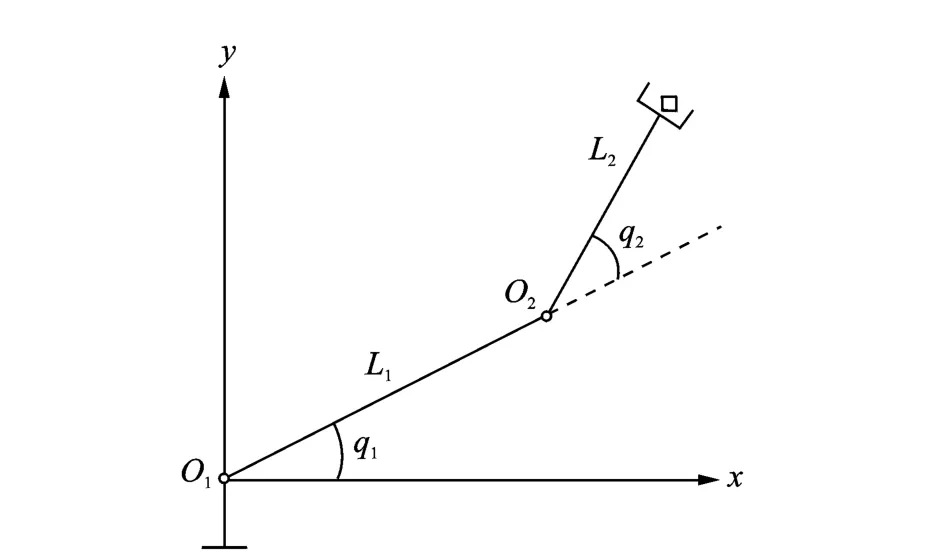
图1 2关节机械臂示意图Fig.1 2 joint manipulator diagram

2 反演非奇异终端的神经滑模控制器

2.1 反演非奇异终端的滑模控制

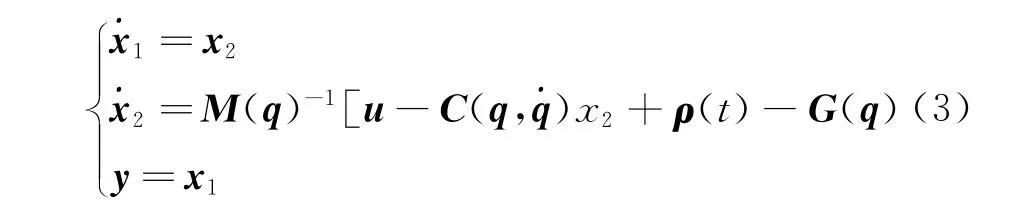
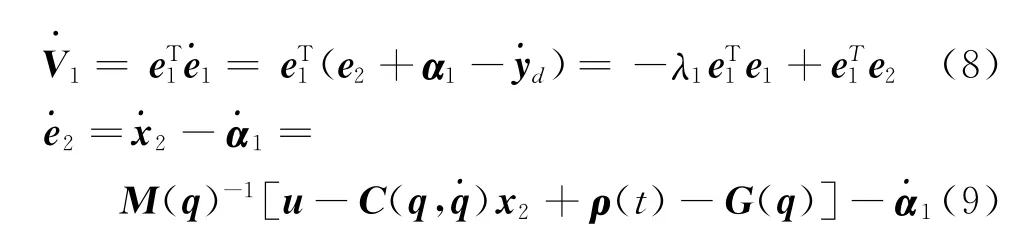
非奇异终端的滑模面定义为

其中：y为关节角的位置矢量。

对关节位置的跟踪偏差定义为

其中：yd为期望值，且yd拥有2阶导数。

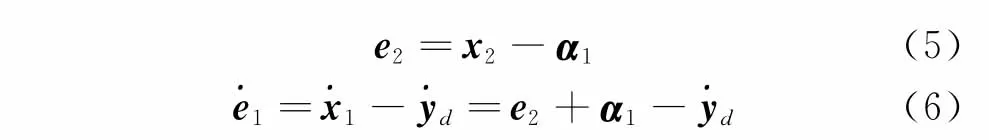
虚拟控制项定义为

其中：λ1＞0。

选取Lyapunov函数

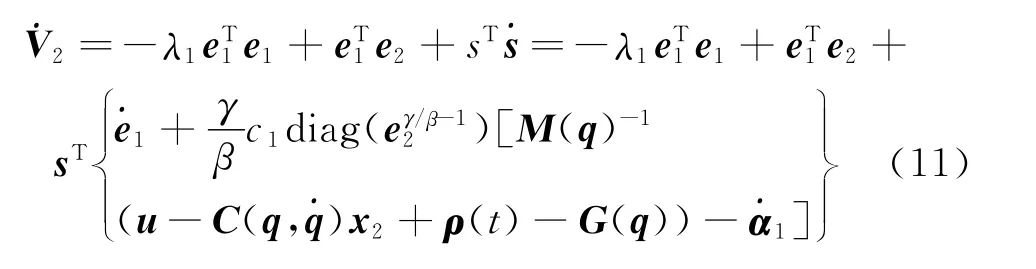
选取Lyapunov函数选取控制律为

其中：¯ρ（t）为不确定因素的上界。

定理1式（1）表示的动力学方程为式（1）的2阶机械臂，式（10）表示非奇异终端的滑模面。若u= u0+u1+u2+u3为反演的滑模控制律，其中u0，u1，u2，u3如式（13）～（16）所示，则系统可以逐渐达到稳定点。

选取Lyapunov函数

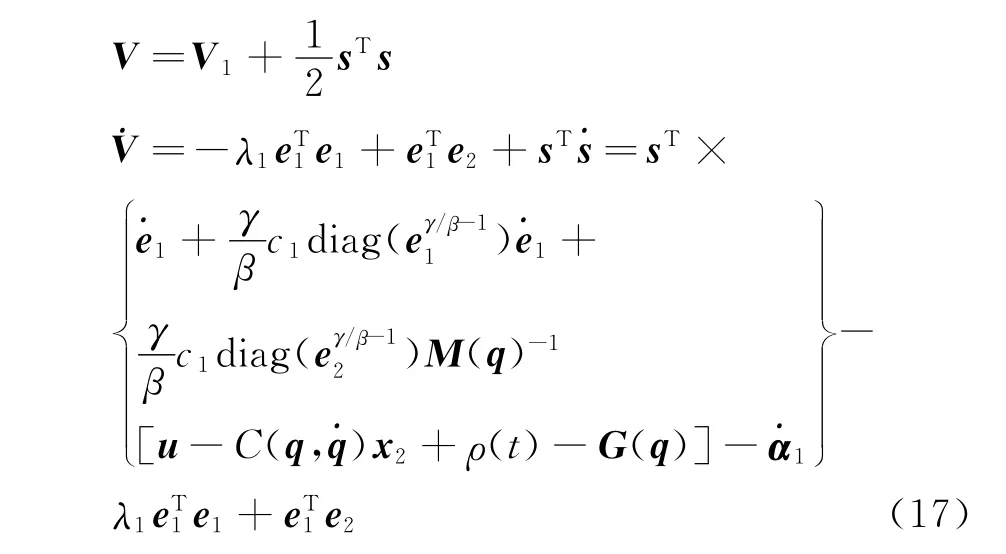
把式（12）代入式（17），得

可见，设计的反演非奇异终端的滑模控制系统具有稳定性。

2.2 RBF神经网络的控制器

在实际的控制系统中，通常设计RBF网络来逼近¯ρ（t）（不确定性上界），原因是¯ρ（t）很难确定，RBF网络系统输入X=（e，˙e）T（跟踪路径的偏差与偏差的变化率），输出为¯ρ（t）（参数上界估计值），则

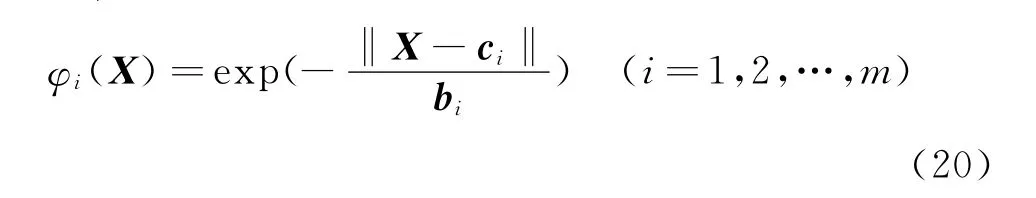
其中：φi（X）为高斯函数；ˆWT为RBF神经网络的权值。其中：bi为节点i的神经元宽度；ci为网络第i个节点的中心矢量。

定理2式（1）表示的动力学方程为式（1）的2阶机械臂，式（10）表示非奇异终端的滑模面。若u= u0+u1+u2+u3为反演非奇异终端的神经控制律，其中u0，u1，u2，u3如式（13）～（16）所示，RBF神经网络的控制器的输出为¯ρ（t）。

假设1 W*TΦ（X）-¯ρ（t）=ε（X）为RBF神经网络最优权值W*符合的条件，且‖ε（X）‖＜ε1。

假设2 ¯ρ（t）-‖ρ（t）‖＞ε0＞ε1为不确定因素上界符合的条件，则系统可以逐渐达到稳定点。

选取Lyapunov函数

其中：~W=W*-ˆW。

则

适应算法的在线调整权值可以设计为

则

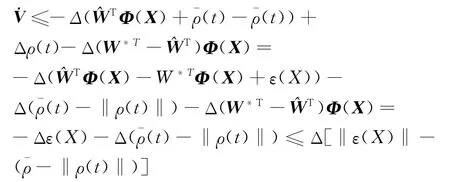
通过假设1和假设2获得‖ε（X）‖-（¯ρ-‖ρ（t）‖）＜ε1-ε0，即˙V＜0成立。

因此，设计的反演非奇异终端的神经滑模控制系统具有稳定性。

3 系统仿真

2关节的机械臂系统其动力学数学模型为

反演非奇异终端的滑模控制仿真结果如图2所示。反演非奇异终端的神经滑模控制如图3所示。系统的跟踪误差的相轨迹图如图4所示。其中：q2（t）为关节2实际角位移的运行轨迹；u2（t）为关节2的控制输入；r2（t）为关节2的期望角位移的运行轨迹；q1（t）为关节1的实际角位移的运行轨迹；u1（t）为关节1的控制输入；r1（t）为关节1的期望角位移的运行轨迹。

当从初始状态到跟踪误差小于0.02 r/min以后，反演非奇异终端的神经滑模控制器的输出抖振范围为［-0.540 5，2.707 6］（N·m）与［-2.551 7，2.405 2］（N·m），反演非奇异终端的滑模控制关节1，2输出的抖振范围为［-11.323 4，4.419 52］（N·m）与［-11.077 1，10.332 2］（N·m）。

当从初始状态到跟踪误差小于0.02 r/min时，别从［-11.323 4，4.419 52］（N·m）与［-11.077 1，10.332 2］（N·m）减小到了［-0.540 5，2.707 6］（N·m）与［-2.551 7，2.405 2］（N·m）。同时，与反演非奇异终端的滑模控制的轨迹跟踪误差速度相比，反演非奇异终端的神经滑模控制的轨迹跟踪误差速度比较快，所需时间分别从1.775 2 s与1.833 4 s减少到了1.506 2 s与1.569 8 s。

图2 反演非奇异终端滑模控制Fig.2 Inversion of the non-singular terminal sliding mode control

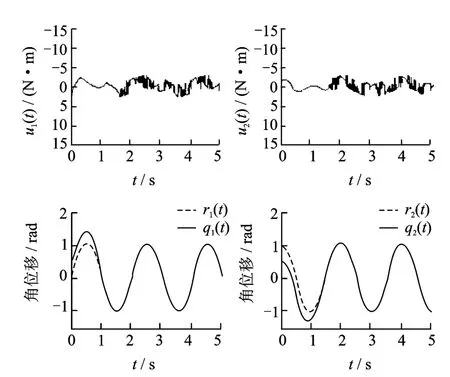
图3 反演非奇异终端神经滑模控制Fig.3 Inversion of the non-singular terminal neural sliding mode control

图4 跟踪误差相轨迹图Fig.4 Phase trajectory tracking error

反演非奇异终端的神经滑模控制关节1，2需要的时间为1.506 2 s与1.569 8 s，反演非奇异终端的滑模控制关节1，2需要的时间为1.775 2 s与1.833 4 s。

可见，反演非奇异终端的神经滑模控制器输出的抖动显然减小了许多，关节1，2输出抖振范围分

4 结束语

提出了一种反演非奇异终端的神经滑模控制的方法，解决了具有外部干扰以及建模误差的机械臂轨迹跟踪存在的问题，该方法也适于解决多关节机械臂轨迹跟踪问题。为了实现对外部干扰以及建模误差的自动跟踪，设计了RBF神经网络的自适应律。采用Lyapunov定理证明了反演非奇异终端的神经滑模控制系统的稳定性。仿真分析结果表明，该方法不仅可以削弱控制系统中存在的抖振现象，且具有较好的轨迹跟踪性能，使得对于外部干扰以及建模误差等因素的鲁棒性得到了较大的提高。

［1］ Lin Faa-Jeng，Shen Pengheng.Adaptive backstepping sliding mode control for linear induction motor drive ［J］.Electric Power Applications，IEEE Proceedings，2002，149（3）：183-193.

［2］ Liu Jinkun，He Yuzhu.Fuzzy global sliding mode control based on genetic algorithm and its application for flight simulator servo systemr［J］.Chinese Journal of Mechanical Engineering，2007，20（3）：11-17.

［3］ Ge Lianzheng，Zhao Lijun.Target tracking algorithm using finite-time convergence smooth second-order sliding mode controller for mobile robots［J］.Chinese Journal of Mechanical Engineering，2011，24（3）：86-91.

［4］ 陈卫东，唐得志，王海涛.基于Backstepping的机器人鲁棒性跟踪控制［J］.系统仿真学报，2004，16（4）：837-838.Chen Weidong，Tang Dezhi，Wang Haitao.Robust tracking control of robotic manipulator based on backstepping［J］.Journal of System Simulation，2004，16（4）：837-838.（in Chinese）

［5］ 李升波，李克强，王建强.非奇异快速的终端滑模控制方法［J］.信息与控制，2009，38（1）：1-8.Li Shengbo，Li Keqiang，Wang Jianqiang.Nonsingular and fast tenrninal sliding mode control method［J］.Information and Control，2009，38（1）：1-8.（in Chinese）

［6］ Lin Chuankai.Nonsingular terminal sliding mode control of robot manipulators using fuzzy wavelet networks［J］.IEEE Transactions on Fuzzy Systems，2006，14（6）：849-859.

［7］ Feng Y，Yu X H，Man Z H.Non-singular terminal sliding mode control of rigid manipulators［J］.Automatica，2002，3（8）：2159-2167.

［8］ 李志军，邓子辰，顾致平.ATMD结构基于补偿器的准滑模控制［J］.振动、测试与诊断，2012，32（6）：909-914.Liu Zhijun，Deng Zichen，Gu Zhiping.Quasi-sliding mode control with compensator for ATMD-buildings ［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2012，32（6）：909-914.（in Chinese）

［9］ 占金青，胡俊峰，张宪民.基于趋近律离散滑模控制的柔性梁振动抑制［J］.振动、测试与诊断，2012，32（2）：186-191.Zhan Jinqing，Hu Junfeng，Zhang Xianmin.Vibration suppression of flexible beam based on discrete sliding mode control with reaching law［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2012，32（6）：186-191.（in Chinese）

［10］魏承，赵阳，王洪柳.基于滑模控制的空间机器人软硬性抓取［J］.机械工程学报，2011，47（1）：43-47.Wei Cheng，Zhao Yang，Wang Hongliu.Space robot soft-hard grasping based on sliding mode control［J］.Journal of Mechanical Engineering，2011，47（1）：43-47.（in Chinese）

［11］贾庆轩，张晓东，李梅峰.空间机械臂关节积分反演滑模控制研究［J］.系统仿真学报，2009，21（10）：3014-3016.Jia Qingxuan，Zhang Xiaodong，Li Meifeng.Integral backstepping sliding-mode control for space manipulator joint［J］.Journal of System Simulation，2009，21（10）：3014-3016.（in Chinese）

［12］张袅娜.参数不确定柔性机械手的神经滑模控制［J］.机械工程学报，2011，47（1）：31-42.Zhang Niaona.Neural sliding mode control for flexible manipulators with uncertain parameters［J］.Journal of Mechanical Engineering，2011，47（1）：31-42.（in Chinese）

［13］穆效江，陈阳舟，张利国.多关节机器人的非奇异终端模糊滑模控制［J］.北京工业大学学报，2008，34（9）：920-924.Mu Xiaojiang，Chen Yangzhou，Zhang Liguo.Fuzzy nonsingular terminal sliding mode control for multilink robots［J］.Journal of Beijing University of Technology，2008，34（9）：920-924.（in Chinese）

［14］Shafiou I，Liu X P.Robust sliding mode control for robot manipulators［J］.IEEE Transactions on Industrial Electronics，2011，58（6）：2444-2453.

TH122；TP273

10.16450/j.cnki.issn.1004-6801.2015.04.014

贾育秦，男，1954年12月生，教授、硕士生导师。主要研究方向为现代制造技术。曾发表《基于小波分析的超精密数控加工过程误差控制策略》（《机床与液压》2006年第6期）等论文。E-mail：tyhmijyq@163.com

简介：胡晓雄，男，1988年9月生，硕士研究生。主要研究方向为现代制造技术。

E-mail：hxx0903@163.com

*国家自然科学基金资助项目（51205224）；国家重点基础研究发展计划（“九七三”计划）资助项目（2013CB035802）；国家高技术研究发展计划（“八六三”计划）资助项目（2012AA091103）；国家科技支撑计划资助项目（2012BAI07B04）；中央高校基本科研业务费专项资金资助项目（TD2011-25）；中国博士后科学基金资助项目（201104597）

2013-06-15；

2013-08-12