复小波分解联合SVD提取振动信号非平稳特征*

赵 玲，刘小峰，娄 路（.重庆交通大学信息科学与工程学院 重庆，400074）（.重庆大学机械传动国家重点实验室 重庆，400044）

复小波分解联合SVD提取振动信号非平稳特征*

赵 玲1，刘小峰2，娄 路1
（1.重庆交通大学信息科学与工程学院 重庆，400074）（2.重庆大学机械传动国家重点实验室 重庆，400044）

针对齿轮箱故障信号的多分量多频调制特点，提出了一种基于奇异值分解的最优小波解调技术。首先，采用小波变换的最小Shannon熵作为时间尺度分辨率的度量指标，将其应用到Morlet分析小波的参数优化选择中；其次，对常规小波参数选择方法进行了改进，利用奇异值分解技术对最优小波变化尺度进行了迭代搜索。该方法可以很好地降低噪声信号，有效提取信号中的周期成分，具有较好的瞬态信息提取能力。试验结果也表明了该方法在齿轮箱故障特征提取中的重要性以及降噪方法的有效性。

奇异值分解；连续小波变换；参数选择；特征提取

引 言

利用振动信号的诊断方法是故障诊断技术中最有效的方法之一。设备早期故障信号包含尖峰、突变的非平稳信号，还可能包含非平稳的白噪声，这些是信号的高频部分［1-2］。受到设备运行环境、电磁干扰和采样仪器的限制，采集到的数据中不可避免地含有噪声。由于信号中包含的故障信息一般较弱，常淹没在噪声信号中，所以必须对信号进行消噪处理，需要在消除噪声所表现的高频量的同时，保留反映信号突变部分的高频量。

解析小波变换是一种特殊的连续小波变换，其小波参数的选择非常灵活，在低频段具有细致的信号刻画能力，可以有效分析信号内部分量的相位和包络幅值［3-5］。对于强噪声背景下的微弱突变信号的提取采用常规的解析小波变换去噪方法就显得有些困难，需要对分析小波的参数进行最优化的选择［6］。笔者采用奇异值分解技术联合复解析小波解调法可实现良好的降噪效果并提取出有效成分进行诊断分析。

1 奇异值分解的基本理论

奇异值分解（singular value decomposition，简称SVD）是非线性滤波方法，广泛应用于信号的降噪和检测。它从矩阵的角度出发，将包含信号信息的矩阵分解为一系列奇异值以及奇异值矢量对应的时频子空间，在信号处理和统计学等领域有重要应用［7］。奇异值分解具有理想的去相关特性。基于SVD的信号分析方法可以对信号进行重构，较好分离出有用信号的特征信息，在故障诊断领域已有成功应用。

设A为M×N阶矩阵，矩阵A可表示为

其中：U为M×M阶正交矩阵；V为N×N阶正交矩阵；D=diag（σ1，σ2，σ3，…σn）为M×N阶对角矩阵，D的对角元素σi称为矩阵A的奇异值，且σ1≥σ2≥…≥σM≥0（M＜N）。

由于D为对角阵，因此SVD可以将一个秩为r 的m×n阶矩阵D表示为r个秩为1的m×n阶子矩阵之和。每个子矩阵由两个特征向量（矩阵U和矩阵V）和权值相乘得到，即式（1）可表示为

其中：r为矩阵A的秩，上标T表示转置；ui为矩阵AAT的第i个特征向量；vi为矩阵ATA的第i个特征向量；Ai为包含ui和vi的子矩阵；uivTi为单秩M×N阶矩阵，表示矩阵的第i个特征图像，它们形成一个正交基，可用来重建矩阵A。

若设矩阵ATA或AAT的特征值为λi，可以证明

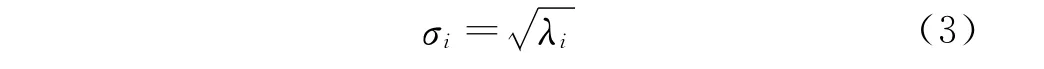
由于奇异值是按数值从大到小顺序排列的，所以前面几个特征值作用最大。如果矩阵A的秩为r（r＞0），那么A存在着r个正的奇异值，即σr＞0，σr+1，…，σM=0。如果矩阵A为满秩M，则所有的奇异值都不为零。

式（2）表明，矩阵A经过SVD变成一系列的子矩阵Ai和其对应的奇异值σi（反映该子矩阵包含信息的多少），也就是将矩阵分解成相互正交的子空间，从而将矩阵包含的信息分解到不同的子矩阵中。在实际应用中，若A表示时频信息，那么对应的ui和vi分别表示频率和时间信息。通常而言，对式（2）的应用是根据有效的奇异值个数k得到A的估计值ˆA，从而实现信号的降噪和有用信号的提取［8-9］，即

2 复解析小波解调法

复解析小波变换是一种特殊的连续小波变换，其小波参数的选择非常灵活，在低频段具有细致的信号刻画能力，可以有效分析信号内部分量的相位和包络幅值。由于Morlet小波具有良好的时频局部化能力，解析小波变换通常采用Morlet作为分析小波［10］。Morlet小波函数的表达式为

其中：σ为正实数，它决定小波时域和频域的宽度，控制小波形状的参数；ω0也为一正实数，它确定了小波的衰减振荡频率。

将φ（t）伸缩平移后得到一个子波簇，即

其中：a为尺度参数；b为位置参数。

设s（t）为能量有限信号，关于小波函数φ（t）的连续小波变换为

其中：φ*（t）为φ（t）的复共轭；s（ω）和φ（ω）分别为s（t）和φ（t）的傅里叶变换。

式（7）相当于利用带通滤波器φ（2πaf）对s（t）进行带通，该滤波器的中心频率和带宽是随尺度变化而变化。小波变换的系数Cs（a，b）为复函数，即

其中

在尺度a下s（t）分量幅值为

小波包络解调谱为

其中：FFT为快速傅里叶变换。

算法流程图如图1所示。

图1 复解析小波解调法Fig.1 Complex analytical wavelet demodulation

3 小波参数优化选择

机械测试中许多特征信号表现为瞬态的冲击信号，Morlet小波函数为平方指数衰减的余弦信号，其波形与冲击信号十分相像，非常适于这类信号的检测。笔者采用最小Shannon熵方法和奇异值分解技术相结合来设计最佳的Morlet小波及变换尺度a。

在信号检测及故障诊断中，希望能够突出特征成分抑制无关成分，这种情况下的参数选择需要使基小波与特征成分尽量相似，通常采用“稀疏性（sparse）”作为相似程度的评价，认为使小波变换后的系数矩阵最稀疏的小波函数与信号最相似。最小Shannon熵就是一种很好“稀疏性”评价标准［11］。

（p1，p2，…pn）为一不确定的概率分布，根据这一理论，最不确定的概率分布（等概率分布）具有最大的熵值；同时，概率分布越接近这种等概率分布，其熵值也就越大，Shannon熵值的大小反映了概率分布的均匀性。如果把小波变换的系数处理成一个概率分布序列，由它计算得到的熵值就反映了这个系数矩阵的稀疏程度，这种熵称作小波熵。因此，当小波熵最小时对应的基小波就是与特征成分最匹配的小波。在一定的范围内变化σ，选择使得信号小波熵最小的σ，a作为最优值，从而确定了与信号特征成分十分相似的最佳Morlet小波，此方法就是基于Shannon小波熵的参数选择方法。

通过最小Shannon熵标准确定了基小波的形状参数σ，而小波滤波的频率响应是同时随着基小波ψ（t）的形状参数σ和尺度参数变化而变化的。参数a控制着小波滤波的频带范围，通过选取适当的a，就可以很好地提取含噪信号中的周期冲击信号。

假设一个周期信号X=［x1，…，xl］的周期为n，将信号X按如下矩阵重新排列，矩阵的每一行恰好包含一个周期的数据

其中

由于矩阵X有m个重复的行且矩阵的秩为1，因此信号仅有一个非0的奇异值σ1和m-1个0奇异值。

假设一个含噪声的周期信号X=［x1，…，xl］，其周期仍然为n，由于噪声信号的幅值是随时间变化而不规则变化的，可按式（13）的方式重新排列成M1×N1的矩阵，矩阵的每一行包括N1个序列。由于噪声的影响，矩阵的秩为满秩m，并且当N1=n时，奇异值σ1为最大，即比率

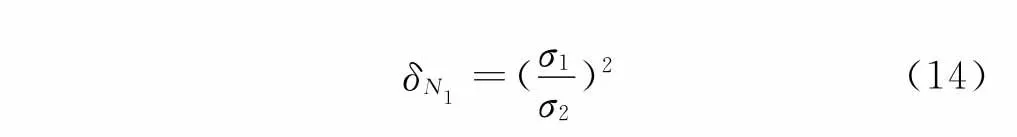
也最大。因此，可用δN1来评价信号的周期性，从而计算出最佳尺度参数a。

计算出基小波的最佳形状参数σ和尺度参数a后，就可以按式（11）得到信号的小波包络解调谱。

4 试验分析

在齿轮箱故障诊断中，齿轮、轴或滚动轴承发生故障时，往往会出现以齿轮所在轴的转频或滚动轴承通过频率为调制频率的调制边频带，应用解调分析就可以提取出调制频率，分析其强度和频次就可以判断齿轮箱的故障部位和损伤程度［12］。据此，下面采用本研究方法对低速齿轮上存在磨损故障的齿轮箱振动信号进行分析。

图2为齿轮传动故障检测试验装置。齿轮箱为两级变速，低速部分啮合齿轮的齿数比为41∶37，大齿轮所在轴的转速为600 r/min，计算出齿轮的啮合频率为410 Hz，大齿轮所在轴的转频为10.0 Hz，小齿轮所在轴的转频为11.081 Hz。通过安装在箱体表面上的加速度传感器，用30 k Hz的采样频率测得的变速箱Ⅱ档运行时的振动信号如图3所示。为去除高次谐波的影响，模拟滤波器上限截止频率为3 k Hz。

图2 试验装置及故障齿轮Fig.2 Experimental installation and the gear

图3 振动信号时域波形Fig.3 Wave of the vibration signals

首先，采用最小Shannon熵方法确定出最优morlet小波的形状参数为σ=470。然后，初始化一个尺度变化范围a∈［1，32］，利用奇异值分解技术确定最佳变换尺度a，变化步长为0.1，当式（14）表示的值为最大时的a即为最佳尺度值，通过计算得出当尺度a=6.1，比率δN1最大，此时能更好地提取信号的周期冲击信号。确定了形状参数a和变换尺度β后，就可以对信号进行滤波消噪处理。去噪后的故障信号如图4所示，信号的信噪比提高21.2％，其去噪效果相当明显。

图4 去噪后的振动信号时域波形Fig.4 Wave of the signals after noise reduction

尺度为a=6.1时分解出的为最优小波系数包络幅值谱如图5所示。进行解调分析并细化得到最优小波系数的解调细化谱如图6所示。

图5 最优小波系数的包络幅值谱Fig.5 Envelop spectrum of optimal wavelet coefficient

图6 最优小波系数解调细化谱Fig.6 Detailed spectrum of optimal wavelet coefficient

图6中的主频成分为小齿轮所在轴的转频11.093 Hz（与理论值11.081 Hz非常接近）及其倍频22.174 Hz。结合频谱分析的结果可断定是小齿轮出现了磨损或断齿故障，事实上本试验装置中轴2上的小齿轮确实出现了磨损缺陷。采用本研究方法得到的齿轮故障诊断结果与事实是相符合的，进而验证了该方法的可行性。

5 结束语

齿轮出现故障时，振动信号表现为多分量调制特征，复解析小波变换具有自适应带通滤波能力，能够灵活地选择变化尺度分离出故障分量所在的频段并进行解调分析。笔者提出的复解析最优小波的解调方法对分析小波参数进行了优化选择，可以很好地降低噪声信号，有效提取信号中周期成分，具有较好的瞬态信息提取能力，能准确捕捉到信号的故障信息。试验验证了采用本研究方法提取出的齿轮故障信号的边带结构更加清晰，提高了齿轮故障诊断的准确性。

［1］ Lin Jin，Zuo M J.Gearbox fault diagnosis using adaptive wavelet filter［J］.Mechanical System and Signal Processing，2003，17（6）：1260-1269.

［2］ 程军圣，张亢，杨宇.局部均值分解方法在调制信号处理中的应用［J］.振动、测试与诊断，2010，30（4）：362-364.Cheng Junsheng，Zhang Kang，Yang Yu.Application of local mean decomposition method to the processing of modulated signals［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2010，30（4）：362-364.（in Chinese）

［3］ 李辉，郑海起，唐力伟.瞬时频率估计的齿轮箱升降速信号阶次跟踪［J］.振动、测试与诊断，2007，27（2）：125-128.Li Hui，Zheng Haiqi，Tang Liwei.Order tracking of speed up signal for gearbox based on instantaneous frequency estimation［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2007，27（2）：125-128.（in Chinese）

［4］ 罗洁思，于德介，彭富强.齿轮箱故障振动信号的阶比多尺度形态学解调［J］.机械工程学报，2010，46（11）：114-118.Luo Jiesi，Yu Dejie，Peng Fuqiang.The order multiscale morphology demodulation of the vibration signal of a fault gearbox with rotating speed fluctuation［J］.Journal of Mechanical Engineering，2010，46（11）：114-118.（in Chinese）

［5］ 杨国安.机械设备故障诊断实用技术［M］.北京：中国石化出版社，2007：186-203.

［6］ 梁霖，徐光华.基于自适应复平移Morlet小波的轴承包络解调分析方法［J］.机械工程学报，2006，42（10）：151-154.Liang Lin，Xu Guanghua.Optimal envelope demodulation method based on adaptive complex shifted morlet wavelet in bearing diagnosis［J］.Journal of Mechanical Engineering，2006，42（10）：151-154.（in Chinese）

［7］ 赵学智，叶邦彦，陈统坚.基于小波-奇异值分解差分谱的弱故障特征提取方法［J］.机械工程学报，2012（7）：37-48.Zhao Xuezhi，Ye Bangyan，Chen Tongjian.Extraction method of faint feature based on wavelet-SVD difference spectrum［J］.Journal of Mechanical Engineering，2012（7）：37-48.（in Chinese）

［8］ 陈恩利，张玺，申永军，等.基于SVD降噪和盲信号分离的滚动轴承故障诊断［J］.振动与冲击，2012，23（3）：185-190.Chen Enli，Zhang Xi，Shen Yongjun，et al.Fault diagnosis of rolling bearings based on SVD denoising and blind signals separation［J］.Journal of Vibration and Shock，2012，23（3）：185-190.（in Chinese）

［9］ 程发斌，汤宝平，赵玲.最优Morlet小波滤波及其在机械故障特征分析中的应用［J］.中国机械工程，2008（12）：1437-1441.Cheng Fabin，Tang Baoping，Zhao Ling.A filtering method based on optimal morlet wavelet and its application in machine fault feature analysis［J］.China Mechanical Engineering，2008（12）：1437-1441.（in Chinese）

［10］申建红，李春祥，李锦华.基于解析小波变换识别结构的模态阻尼参数［J］.振动与冲击，2009，28（10）：89-93.Shen Jianhong，Li Chunxiang，Li Jinhua.Identifying structural modal damping parameters based on analytic wavelet transformation［J］.Journal of Vibration and Shock，2009，28（10）：89-93.（in Chinese）

［11］Karvanen J J，Cichocki A A.Measuring sparseness of noisy signals［C］∥Proceedings of the 4th International Symposium on Independent Component Analysis and Blind Signal Separation（ICA2003）.Nara，Japan：［s.n.］，2003：125-130.

［12］Le T P，Argoul P.Continuous wavelet transform for modal identification using free decay response［J］.Journal of Sound and Vibration，2004，277：73-100.

TH115；TP395.02

10.16450/j.cnki.issn.1004-6801.2015.04.012

赵玲，女，1979年11月生，博士、副教授。主要研究方向为信号处理、设备状态监测与诊断。曾发表《Fault diagnosis method based on fractal theory and application in wind power systems》（《Journal of China Ordnance》2012，No.3）等论文。

E-mail：zhao.ling@163.com

*国家自然科学基金资助项目（61304104）；重庆市自然科学基金资助项目（cstc2015jcyj A0540）

2013-05-13；

2013-07-30