基于第2代小波的有限元模型更新方法*

张 欣，刘 洋，高丹盈（郑州大学土木工程学院 郑州，450001）

基于第2代小波的有限元模型更新方法*

张 欣，刘 洋，高丹盈
（郑州大学土木工程学院 郑州，450001）

提出了有限元模型更新刚度曲线的低分辨率表示方法。基于有限的实验模态信息，通过遗传算法得到了更新刚度曲线在低分辨率表示时的尺度函数系数和小波系数。利用多分辨率分析方法实现了复杂精细有限元模型的几何降维，获得了在有限模态参数范围内与精细模型相似的简单有限元模型，并在此简单模型基础上实现了最终的模型更新与损伤识别。证明了从多分辨率分析的角度出发，利用第2代小波变换的方法能够减少待更新的参数数量，降低模型更新过程的奇异性。以变截面箱梁为例，验证了提出方法对裂缝深度变化和局部裂缝数量变化的鲁棒性。本研究方法也适用于多组裂缝群的辨识。

模型更新；损伤识别；多分辨率分析；小波分析

引 言

有限元模型更新与结构损伤识别均为反分析问题，在实际工程中有广泛的应用。目前，使用较为频繁的方法是通过非线性优化［1-7］或者回归分析［8］等数值方法寻求适合的模型参数向量，用有限元模型的理论模态拟合结构的实验模态，使两者间的误差最小，从而得到能够反映结构实际情况的有限元模型。此类问题具有非常强烈的奇异性［9］：a.模型更新或者损伤识别的结果对所选定的待更新参数集十分敏感；b.非线性优化过程具有极大的不确定性，迭代过程可能会收敛于局部最小值而不是全局最小值，更新结果未必具有实际意义；c.对于比较复杂的结构或者损伤模式，需要建立精细的有限元模型才能正确模拟，所需单元数量众多，需要更新的参数数量也相应增加，需要运用大规模非线性优化算法进行分析。此时，计算结果的稳定性更低，几乎无法得到具有实际意义的结果；d.实验误差对更新结果的影响也不可忽视。因此，有效减少需要更新的参数数量［10-12］是提高模型更新和结构损伤识别效率和可靠度的合理技术路线。

以刚度更新为例，有限元模型的实际刚度即反映结构真实状况的刚度，可以被视为两种成分的叠加：一种成分为理论假设刚度；另一种成分为实验更新刚度。前者的精细度可以任意假定，用于建立高精度的有限元模型，仿真复杂的工程结构。后者由实验确定，精细度无法提高。因此，模型更新的数学实质是在一条高精度（高分辨率）理论刚度曲线上叠加低精度（低分辨率）更新刚度曲线，得到结构的模态参数来拟合实验数据。核心问题是如何使用最少的数据来近似更新刚度曲线。这属于数据压缩技术。数据压缩技术属于多分辨率分析的范畴，在影音图像处理领域有很多的成熟应用，使用频率较高的应属小波变换。

笔者首先介绍多分辨率分析与小波变换的相关背景；然后阐述低分辨率模型更新思想。

1 多分辨率分析与小波变换

1.1 多分辨率分析理论

具有有限能量的一个函数，如结构刚度函数κ（x），属于内积空间L2（R），该空间为无穷维函数线性空间，存在无穷个线性无关向量φk（x｛｝）∞构成的基函数族，k为采样点的位置［13］。则

在该内积空间内存在嵌套式闭子空间逼近序列

其中：尺度函数φ（x-k）为Riesz基，满足双尺度方程

这样构成多分辨率逼近。计Wj=Vj+1/Vj为Vj在Vj+1中的补子空间，则Vj+1=Wj⊕Vj，⊕为子空间直和。依次类推，有

ψ（x）为W0的基函数，称小波函数。W0∈V1，可由φ（x）线性表示

其中：φi，k（x）为低通滤波函数；ψj，k（x）为带通滤波函数；｛hn｝为低通数字滤波器；｛gn｝为高通数字滤波器。

在j尺度层面，函数κ（x）可表示为

其中：~φj，k（x）为φj，k（x）的对偶尺度函数。

其中：~ψj，k（x）为ψj，k（x）的对偶小波函数。

这样就形成κ（x）在j尺度上的近似κj（x）。j数值越大，就越能精确表述原函数，但是所需数据就越多；j数值越小，就会有越多的原函数信息被忽略，κj（x）就越粗糙，变化趋势也越平缓，所需数据点数也越少。基于以上理论就可以实现更新刚度曲线的低分辨率表示。然而，小波变换在无限域进行，当应用于有限元模型更新时，必须考虑结构只在有限范围内存在这一问题，需要考虑小波函数与尺度函数的边界效应。在这一点上，第2代小波［14］有优势，它具有与第1代小波相似的特性且构造简单方便，一般通过提升格式［15］就可以实现有限域上非均匀采样间隔的小波函数和相应尺度函数的构造。

1.2 提升格式与第2代小波函数和尺度函数的构造

提升格式［15］指在简单的小波函数与尺度函数的基础上，通过提升运算，层层加码，形成复杂形式的小波变换。

构造第2代内插型尺度函数与小波函数一般可以选用懒惰小波为提升起点，经过对偶提升（预测）实现合成尺度函数与分解小波的提升，再通过提升过程实现分解尺度函数与合成小波函数的提升。

定义如下多尺度分析算子：从Vj+1到Vj的运算为~H运算，Vj+1到Wj的运算为~G运算，逆运算分别为H运算和G运算。设E为偶下采样算子，D为奇下采样算子，懒惰小波运算为

按下式进行提升

内插滤波运算Hintj可以采用两点、三点、四点或更多点数的内插滤波形式，由此可以产生不同形式的尺度函数与小波函数。

在以上提升格式的基础上，通过迭代算法获得每个尺度相应采样点上的尺度函数与小波函数。因为第2代小波能适应非均匀采样以及边界的影响，在某一个尺度层内小波函数和尺度函数可能会因点而异，各尺度层间也可能互异。

2 低分辨率模型更新

2.1 基本方法

设更新目标为结构的刚度曲线K（x）

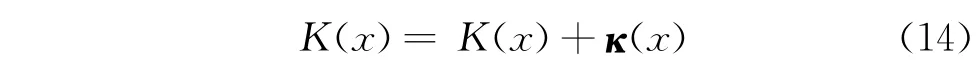
其中：K（x）为结构在x处的理论刚度；κ（x）为更新刚度。

结构的质量分布不更新。根据多分辨率分析理论，在j尺度上，模型的更新刚度函数为

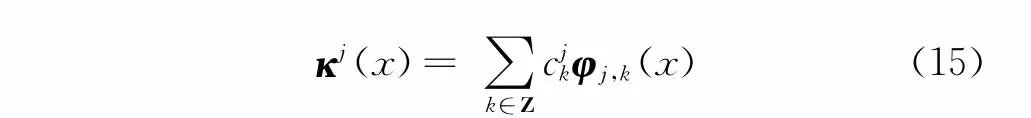
在j+1尺度上为

当前模型结构的模态参量为（λi，φi），i=1，2，…为刚度曲线的函数。其中：λi为第i阶频率；φi为为第i阶振型；实验模态参数为（¯λi，¯φi），i=1，2，…。

定义误差向量

其中：权重矩阵为

在优化求解过程中可以强调某一阶模态信息的重要性，也可以降低该信息的重要性。这可以通过调整权重矩阵对角元素的大小来实现。第i阶振型的相关因数为

其中：¯φi，φi分别为目标和当前振型；*代表共轭转置。模型修正的目标是使r（α）的模最小

2.2 两阶段更新模式

r（α）的模可能不为零，因为即使当r（α）的维数，即方程个数大于或等于修正向量α的维数时，非线性方程r（α）=0也可能无解。因此模型更新及损伤识别过程为参数优化过程，而非定解方程求解问题。

一般希望模型更新能在简单模型上进行。例如，使用梁单元建立图1，2中结构的有限元模型，在此模型基础上进行更新操作。由于计算模型不能够完全拟合原始结构的行为，因此存在模型初始误差。另外，在结构出现损伤之后，由于圣维南现象的影响，结构在损伤附近的力学行为更趋复杂，用梁单元不能精确描述，这样就进一步产生了模型更新误差。此外，必然存在的实验误差也会使方程r（α）=0无解。此问题不能通过加入高阶模态信息来解决。例如，对于四点内插滤波，当有两阶模态信息时，理论上可以实现0尺度分辨率的定解更新，当有四阶模态信息时，可以实现1尺度分辨率的定解更新。依次类推。理论上，当有足够模态信息时，可以在足够精细的尺度层面上实现定解更新。然而，随着模态阶数的不断升高，理想梁模型的行为就越发背离实际结构，由此将产生更大的模型误差。

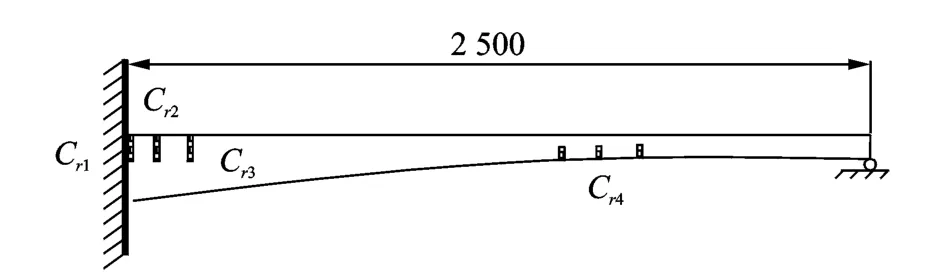
图1 算例结构简图（单位：mm）Fig.1 Sketch of the structure under study（unit：mm）

笔者建议根据结构自身的特性，采取适当阶数的模态信息，分以下两个阶段进行模型更新和损伤识别。

1）模型的初始校准阶段。以图1，2所示结构为例。首先，建立结构的精细有限元模型；然后，根据结构几何特征计算等效梁的刚度曲线建立梁单元模型。此时简化模型的模态参数与精细模型的模态参数不同。依照本研究模型更新方法，得到低分辨率更新刚度曲线，叠加在几何特征刚度曲线上，作为模型初始校准后的刚度曲线。

图2 结构两端横断面（单位：mm）Fig.2 Cross section of two ends（unit：mm）

2）模型的损伤更新阶段。如图1所示，在模型中引入结构损伤，此时模型的模态参数发生变化。在前一阶段刚度曲线的基础上，重复低分辨率更新过程，拟合有损伤模型的模态参数，获得表征结构损伤特性的尺度函数与小波函数系数以及相应的损伤刚度更新曲线。

2.3 近似误差

由于更新刚度曲线是在较低分辨率层面上实现的，因此可能会出现re（αe）残差较大的情况。只有在较高分辨率层上实现更高分辨率的更新刚度曲线，才能从根本上解决这一问题。然而，更新曲线的分辨率由实验结果决定，因此在一般情况下不太可能得到太高分辨率的更新曲线。这也是反分析问题的根本症结之一：根据低分辨率实验获得高分辨率反分析结果，实现所谓的“超分辨率”表述是困难的。

另外，在更新刚度曲线形状比较复杂而曲线实现的分辨率层又比较低时，会出现更新曲线线形失真的现象。这种现象与信号处理中采用较低的采样频率记录较高频率信号而产生的信号失真现象类似，是一种客观现实，不能逾越，其后果不易预测。因为更新刚度曲线的低尺度表示是嵌套在结构模态参数求解运算这一非线性运算过程中的，此时误差讨论极为困难，因此应校验临近尺度层参数更新结果的收敛性，以保证更新结果的正确性。

3 数值算例

在损伤识别的过程中，如果更新过程在复杂、精细的有限元模型上进行，则显得不够经济有效，所以一般希望能在简单有限元模型上进行。但是，对于具有复杂结构形式或损伤方式的结构，只有建立复杂精细的有限元模型，才能较好地仿真，因此产生矛盾。解决方案是先建立精细的有限元模型，获得理论模型模态，再建立简化模型，通过低分辨率更新方法将简化模型的刚度进行更新，得到在有限模态范围内能基本反映精细模型的简单有限元模型，在此基础上再以实验模态为目标更新并得到损伤信息。

3.1 复杂有限元模型的降维近似

以图1，2所示的变截面箱梁为例，弹性模量为3×1010Pa，泊松比为0.2，这里仅考虑竖向振动模态。以板单元建立三维精细参照模型，单元总数为7 500。在固定端处释放上部部分节点，仿真结构竖向裂缝。采用ANSYS计算得到两种工况模态参数如表1所示。梁单元每个节点仅考虑竖向和扭转两个自由度。单元总数为128，每个单元惯性矩由截面几何尺寸计算得出。

表1 模型竖向振型模态参数Tab.1 Modal parameters of the vertical modes

计算数据表明，简化模型与精细模型的模态参数存在明显差别，必须对简化模型的单元刚度进行更新。更新目标为无损精细有限元模型。

为考虑模型刚度的多分辨率表示，设梁单元内力虚功为

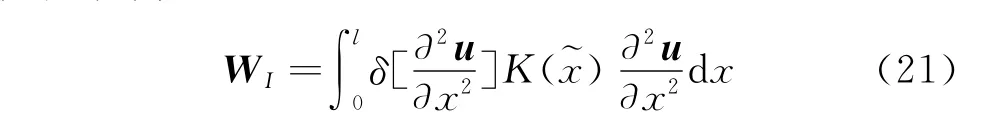
取形函数为q（x），节点位移为u，将K（~x）的多分辨率表达式带入得到单元刚度矩阵元素为

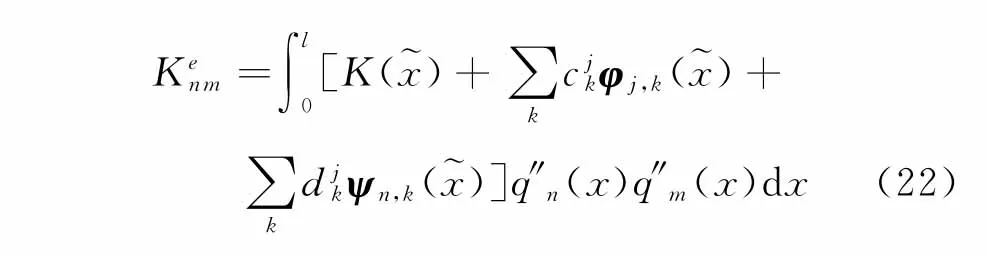
依照式（22）在0尺度分辨率和1尺度分辨率上分别建立有限元模型，计算模态参数更新目标函数r（α）。通过遗传算法求得更新参数，使式（20）最小化。

3.2 模型校准及单裂缝工况计算结果

令djk=0，j=0，得到0尺度层尺度函数系数。令cjk，djk≠0，j=0，得到0尺度层尺度函数系数与小波函数系数，通过式（16）构成1尺度分辨率层刚度函数。这两种更新的结果不尽相同，但基本类似。图3中更新阶段A为一尺度分辨率模型初始校准阶段结果。横坐标1～5为尺度函数系数，6～9为小波函数系数。

图3 模型更新尺度函数与小波函数系数Fig.3 Updating coefficients of the scale function and wavelet function

由小波函数和尺度函数系数合成的更新刚度曲线如图4所示。图4结果表明，三者吻合程度较好，0尺度结果基本收敛于1尺度结果。

在经过初始校准的模型上，针对有损模型的更新结果也绘制在图3，4中，用更新阶段B表示。单元刚度折减曲线如图5所示。

需要说明的是，笔者采用连续函数来表示结构刚度的方法与目前流行的做法不同。目前流行的局部损伤处理方法是采用集中刚度折减法，即将受损单元的刚度降低而相邻单元的刚度保持不变，相当于用方波函数来表示结构刚度的空间变化。这样的做法在单元划分比较粗糙时适用。如果需要精细划分单元则会出现问题，因为从图形分辨率角度来说，由于存在阶跃，理想的方波函数相当于无限分辨率图形，在单元精细划分的情况下需要很多实验信息量才能有效识别。基于有限实验信息，采用低分辨率函数表述刚度折减，就如同对方波函数采取小波分解，只保留缓慢变化的那一部分低分辨率趋势线，从而降低了对实验信息量的要求，但是必然会有信息扩散效应。如图5所示，刚度折减已经扩散到较多单元，这正是信息扩散效应所致。结构损伤的大致位置可以通过刚度折减曲线的谷值位置来判断。

图4 梁模型更新结果Fig.4 Updating results of the beam

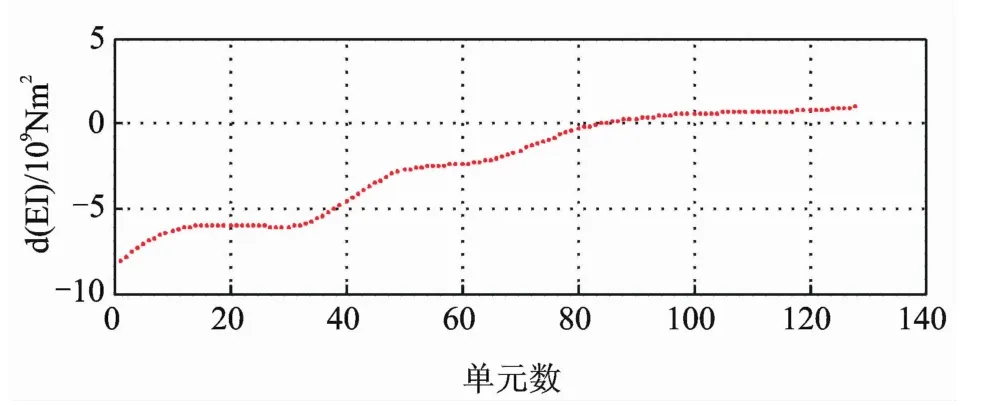
图5 损伤引起的刚度折减Fig.5 Reduction of stiffness

3.3 多裂缝工况计算结果

多裂缝工况由图1中Cr1～Cr4裂缝组合而成。具体组合及相应的前3阶竖向频率如表2所示。表中Y代表采用该项裂缝组合。

表2 损伤状况组合Tab.2 Combination of damages

利用上述方法得到3种损伤组合工况下刚度折减曲线，如图6所示。可以看出：a.因为图6中工况1的裂缝预设深度大于图5，所以图6工况1的刚度折减幅度比图5大，但是折减函数曲线的形状与图5大致相同，说明本研究方法对局部裂缝深度变化具有鲁棒性；b.工况2与工况1相比，由于存在较多的裂缝，因此产生了较大的刚度折减，但是折减函数曲线的形状与工况1大致相同，说明本研究方法对局部裂缝数量变化具有鲁棒性；c.工况3与工况2在梁的左端具有相同的损伤组合，图6表明，两种工况在此处的刚度折减也相仿，说明本研究方法对裂缝群的数量变化具有鲁棒性；d.工况3在80号单元附近有正弯矩区裂缝，表明在该位置有明显的刚度折减，说明本研究方法适用于多组裂缝群的识别。

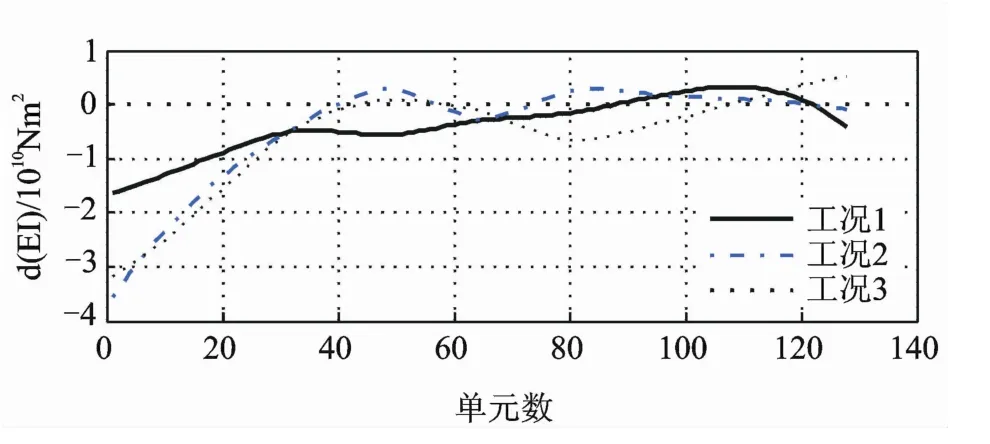
图6 组合损伤工况下刚度折减Fig.6 Stiffness reduction of various damage conditions

4 结束语

基于多分辨率分析的有限元模型更新与损伤识别方法可以在保持结构更新刚度曲线基本特征的前提下，有效减少需要更新的模型参数，降低了非线性优化过程的复杂程度和不确定性。第2代小波是有效的多分辨率分析工具，可应用于有限尺寸结构，符合实际应用条件下结构损伤识别的要求。

在本研究方法的框架内，结构的损伤识别过程可以分解为两个步骤来进行：a.复杂精细有限元模型的几何降维，获得简化模型；b.在简化模型的基础上实现结构损伤识别。以上步骤均可通过多分辨率模型更新方法结合遗传算法实现。该方法具有对裂缝深度变化和局部裂缝数量变化的鲁棒性，并能够适应多组裂缝群的识别。

［1］ Zapico-Valle J L，Alonso-Camblor R，González-Martínez M P，et al.A new method for finite elementmodel updating in structural dynamics［J］.Mechanical Systems and Signal Processing，2010，24（7）：2137-2159.

［2］ Friswell M I，Mottershead J E.Finite element model updating in structural dynamics［M］.Dordrecht：Kluwer Academic Publishers，1999：1-20.

［3］ Teughels A，DeRoeck G.Structural damage identification of the highway bridge Z24 by FE model updating ［J］.Engineering Structures，2003，278：589-610.

［4］ 侯吉林，欧进萍.基于局部脉冲响应的约束子结构修正法［J］.工程力学，2009，26（11）：23-30.Hou Jilin，Ou Jinping.Isolated substructure model updating method based on local impulse response［J］.Engineering Mechanics，2009，26（11）：23-30.（in Chinese）

［5］ 郭力，李兆霞，陈鸿天.基于子结构分析的多重子步模型修正方法［J］.中国工程科学，2006，8（9）：42-48.Guo Li，Li Zhaoxia，Chen Hongtian.Multi-stage model updating method via substructure analysis［J］.Engineering Science，2006，8（9）：42-48.（in Chinese）

［6］ 张保强，陈国平，郭勤涛.使用有效模态质量和遗传算法的有限元模型修正［J］.振动、测试与诊断，2012，32（4）：577-580.Zhang Baoqiang，Chen Guoping，Guo Qintao.Finite element model updating using effective modal mass with genetic algorithm［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2012，32（4）：577-580.（in Chinese）

［7］ Koh C G，Chen Y F，Liaw C Y.A hybrid computational strategy for identification of structural parameters［J］.Computers and Structures，2003，81：107-117.

［8］ Ren Weixin，Chen Huabing.Finite element model updating in structural dynamics by using the response surface method［J］.Engineering Structures，2010，32：2455-2465.

［9］ Vestroni F，Capecchi D.Damage detection in beam structures based on frequency measurements［J］.Journal of Engineering Mechanics，ASCE，2000，126（7）：761-768.

［10］Kim G，Park Y.An automated parameter selection procedure for finite-element model updating and its applications［J］.Journal of Sound and Vibration，2008，309：778-793.

［11］Kim G，Park Y.An improved updating parameter selection method and finite element model update using multi-objective optimization technique［J］.Mechanical Systems and Signal Processing，2004，18：59-78.

［12］Fang S，Perera R，Roeck G.Damage identification of a reinforced concrete frame by finite element model updating using damage parameterization［J］.Journal of Sound and Vibration，2008，313：544-559.

［13］Mallat S.A wavelet tour of signal processing：the sparse way［M］.3rd ed.Singapore：Elsevier，2009：328-338.

［14］Sweldens W.The lifting scheme：a construction of second generation wavelets［J］.Siam Journal on Mathematical Analysis，1997，29：511-546.

［15］Sweldens W.The lifting scheme：a custom-design construction of bi-orthogonal wavelets［J］.Applied and Computational Harmonic Analysis，1996（3）：186-200.

TU311.3；U441；TH113

10.16450/j.cnki.issn.1004-6801.2015.04.010

张欣，男，1971年1月生，博士、教授。主要研究方向为结构动力学。曾发表《Frequency modulated empirical mode decomposition method for the identification of instantaneous modal parameters of aeroelastic systems》（《Journal of Wind Engineering and Industrial Aerodynamics》2012，Vol.101）等论文。

E-mail：zhangxin@zzu.edu.cn

*河南省科技攻关资助项目（112102310453）

2013-05-08；

2013-12-10