利用C语言学习一元线性回归处理

利用C语言学习一元线性回归处理

白 云

(鄂南高中 数学组，湖北 咸宁 437100)

流程图是表示算法的思路是一种极好的方法，它形象直观，各种操作一目了然，不会产生“歧义性”，便于理解，算法出错时容易发现。

C语言是一种通用的、面向过程的结构化程序设计语言。它具有数据类型和运算符丰富多样、语言简洁紧凑、使用方便灵活、表达力强和较高的移植性等特点，从而备受青睐。

本文采用算法中的流程图来讲解一元线性回归处理，并通过C语言编程实现来验证其计算结果的正确性、合理性。

一、一元线性回归处理简介

世界上一切事物的发生和发展都是有原因的，种什么因，结什么果，事物发展的这种因果关系即为事物运动的基本规律。因此，通过对事物内部关系的分析，找出其变化规律，就可以用来预测事物发展变化的趋势。

从数学角度讲，描述这些变量之间的关系，可分为两大类：一类是确定性关系，特点是变量之间有着一一对应(或依从)关系，已知某些量即可求出待求量，即表现为一种函数关系。另一类是非确定性(或相关)关系，例如人的身高与体重，广告支出经费与商品销售收入，施肥量与粮食产量等，它们之间有关系，但却不能由已知某量确定出另外的量，这在数学上称为随机变量关系。随机变量关系却可以通过大量观测数据找出其统计规律，即在大量的偶然现象中找出它们的必然趋势。

通常把研究两个变量间的相关关系叫一元线性回归分析。

表1 相关关系与函数关系的异同点

二、一元线性回归处理的例题及其解答

例题：2011广东高考数学理科第13题题目：某数学老师身高176cm，他爷爷、父亲和儿子的身高分别是173cm、170cm和182cm。因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为______cm.

解答：第一组数据(父亲的身高)，173，170，176，第二组数据为(儿子的身高)170，176，182，列表为：

表2 父亲的身高和儿子的身高

这样的拟合的回归方程为y=x+3，当这个数学老师儿子的身高x=182cm时，他孙子的身高y=185cm。

三、一元线性回归处理的流程图

流程图是一种动态图文，通常用来描述一种过程性的活动，它能直观地描述一个问题求解的具体步骤，对准确的了解事情是如何进行的，以及决定应如何改进过程极有帮助。在一元线性回归处理的流程图中对算法的三大基本结构都有着具体的体现，对学生们学习框图——流程图也有一定帮助。

算法的三大基本结构：(1)顺序结构：描述的是最简单的算法结构，语句与语句之间，框与框之间是按从上到下的顺序进行的。(2)条件分支结构：它是依据指定条件选择执行不同指令的控制结构。(3)循环结构：根据指定条件决定是否重复执行一条或多条指令的控制结构。

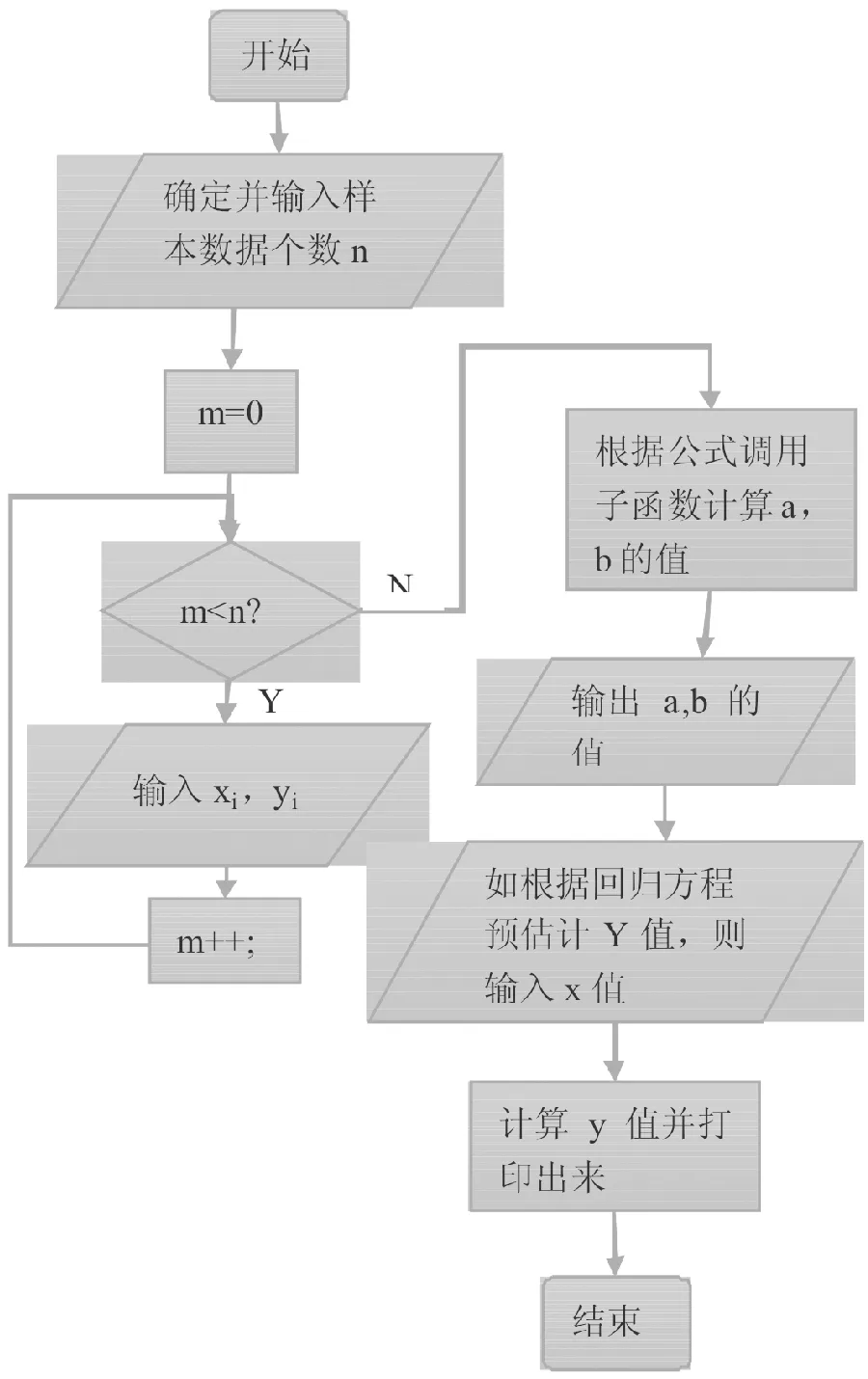
图1 一元线性回归处理的流程图

四、C语言程序设计与实现

#include

#define X 81

#define Y 81

double xy(double *x,double *y,int n)//样本xy的积之和

{int i=0;double sum=0;

for(i=0;i

return sum;

}

double ax(double *x,int n)//样本x的平均数

{int i=0;double average=0,sum=0;

for(i=0;i

average=sum/n;return average;

}

double ay(double *y,int n)//样本y的平均数

{int i=0;double average=0,sum=0;

for(i=0;i

average=sum/n;return average;

}

double xx(double *x,int n)//样本x的平方和

{int i=0;double sum=0;

for(i=0;i

return sum;

}

void main ()//主函数

{int n=0,m=0;//n 样本数据个数，m 记录输入的样本数据个数

int i=0;

double x[X]={0},y[Y]={0};

double a,b;//回归方程的两个系数 y=bx+a;

char s;//用于用户的选择是否进行预估计

double xi=0;//进行预估计的变量

double yi=0;//进行预估计的结果

printf("请确定录入样本数据的个数 n： ");scanf("%d",&n);

printf(" 录入数据的格式为:"x y" ");

//录入样本数据

for(;m

{

printf("第%d组数据：",m+1);scanf("%lf %lf",&x[m],&y[m]);

}

printf(" ");

//打印出所有的样本数据

printf("所有的数据： ");

printf("X");

for(i=0;i

printf(" ");

printf("Y");

for(i=0;i

printf(" ");

//调用子函数计算a,b的值

//根据公式计算

b=(xy(x,y,n)-n*ax(x,n)*ay(y,n))/(xx(x,n)-n*ax(x,n)*ax(x,n));

a=ay(y,n)-b*ax(x,n);

if(a>0)printf("回归方程为 ：y = %gx + %g ",b,a);

else if(a<0)printf("回归方程为 ：y = %gx %g ",b,a);

else printf("回归方程为 ：y = %gx ",b);

//根据回归方程进行预估计

printf(" 是否要根据回归方程进行预估计(Y/N):");

getchar();s=getchar();

switch(s)

{

case 'y':case 'Y':

do

{

printf("请输入预估计变量x： ");scanf("%lf",&xi);

yi=b*xi+a;

if(a>0)

printf("预估计结果 ：y =%g * %g + %g = %g ",b,xi,a,yi);

else if(a<0)

printf("预估计结果 ：y =%g * %g %g = %g ",b,xi,a,yi);

else

printf("预估计结果 ：y =%g * %g = %g ",b,xi,yi);

printf(" 是否继续进行预估计(是任意值；否0)：");

scanf("%lf",&xi);

}while(xi);

break;

case 'n':case 'N':

break;

}

}

五、运行结果验证

根据提示输入相应数据，得到输出结果如图2所示：

图2 一元线性回归处理的例题运行结果

六、结语

从问题的提出即具体的高考真题，到问题的分析确定哪两个变量具有相关关系、相关关系的特点和判断从而提出回归方程，再到通过流程图的方式讲解回归方程的计算流程，最终问题的解决是通过C语言具体实现一元线性回归处理，直接输入具体数据最终得到结果。全文层层递进，以问题的提出、问题的分析、问题的实现为主线对一元线性回归做了全面的讲解，对学生们学习一元线性回归起到了积极的作用。

[1]人民教育出版社.课程教材研究所.数学(选修1-2)[M].北京：人民教育出版社,2010.

2095-4654(2015)10-0195-03

2015-07-08