顾及方向遮蔽性的反距离权重插值法

李正泉，吴尧祥

浙江省气候中心，浙江 杭州310017

1 引 言

空间插值常用于将离散点数据转换为连续曲面，以便更为直观地考察数据要素的空间分布模式。在等值线绘图中，离散点空间插值是绘制等值线的关键基础，插值方法选取不仅影响要素值的空间分布形式，而且还影响着等值线绘制的视觉效果［1－5］。现今多被采用的空间插值方法有反距离权重法、克里金法、样条法、三角剖分法、多项式法、趋势面法等。反距离权重算法简便、普适性强，但仅考虑插值点与样本点的空间距离，没有包含方向相关［6－7］；克里金以空间统计学作为理论基础，使用变异函数度量样点间的空间相关性，可对插值误差进行逐点理论估计，但其变异函数需人为经验选定，且当变异函数为多个组合时，其计算量剧增［8－9］；样条法更为适合高密度的样点内插，而对于稀疏有限的样点该方法多不适合［10－11］；多项式和趋势面的空间插值更多依赖于插值要素固有的空间分布趋势，若样点布局遵从插值要素的空间变化，则可得到理想的插值效果，反之则难以保证插值的合理性［12－13］；基于三角剖分的插值方法可获得高精度的插值曲面，在地表特征表达和地形等高线的绘制中经常使用［14－16］，但该方法也存在类似于克里金的插值缺陷，即算法复杂计算量大，且其插值曲面的等值线棱角过于明显。简而言之，各种空间插值方式均有优缺，并不存在普适最优的插值方法。

在众多空间插值方法中，反距离权重因其插值原理易于理解、算法简单便于实现，且插值后能够保留原样点真值，常被作为离散点空间分析的传统方法之一。但反距离权重未考虑插值点与样本点之间的方向关系，当样点多集中于插值点某个方向时，该方向的样点总权重就会大大增加，而其他方向上的样点因权重过小而常被忽视，空间插值缺少方向均衡性，其插值合理性亦受到质疑［17－18］。另一方面，反距离权重的等值线绘图通常有一弊病，即图中常会有孤立圆区存在，且易在样本极值点周围产生同心圆区（“牛眼”现象）［19－22］，这严重影响了等值线图的审美效果。在大多情况下，为追求绘图美观不得不摒弃反距离权重而选用其他插值方式，不惜以数据失真来换取整幅等值线图的协调美观。本文旨在对反距离权重插值算法进行优化改进，减少或消除反距离权重等值线绘图中不合理的孤立圆和同心圆现象的存在。通过增加一个可反映插值样点方位的调和权重系数K，克服反距离权重插值中仅考虑插值点与样本点之间距离而未考虑它们之间方位的插值缺陷，由此提出了调和反距离权重（adjusted inverse distance weighted，AIDW）空间插值方式。

2 调和反距离权重插值

2.1 反距离权重算法

反距离权重（inverse distance weighted，IDW）算法于1968年由Shepard提出，1985年Watson等将其应用于空间插值的等值线绘制［23－24］，继而IDW算法被广泛应用于各行业领域的空间分析与制图［25］。IDW算法公式通常被表示为

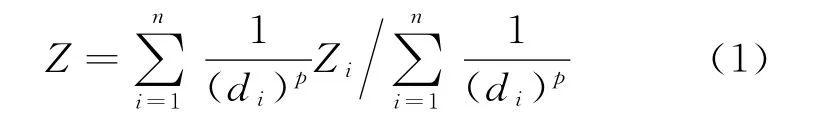
式中，Z是插值点估计值；Zi是第i个样本点观测值；di是插值点与第i个样本点之间的欧氏距离；n是用于估算插值点值的样点数；p是幂指数。在空间分析和等值线绘图软件（如ArcGIS、Surfer等）的计算程序中，p值通常被默认为2，此时IDW被称为距离平方反比法。文献［26］表明随着p值的增大，IDW的插值结果越具有平滑效果。

从IDW算法（式（1））可看出，插值点的估算值仅与插值样本距插值点的远近相关，并未考虑样本点的方位性（即样本点被表示为各向同性）。IDW插值的基本假设是样点在插值区呈均匀分布，当样点在各方向较均匀分布时，该插值算法十分可靠。然而在众多情况下，样点在各向分布并非均匀，甚至会出现样点集中于某一方向的现象，违背了基本假设，其插值合理性就难被保证。针对IDW这一插值局限，本文提出了调和反距离权重（AIDW）插值算法。

2.2 调和反距离权重算法

2.2.1 基本假设

AIDW算法与IDW基本类似，关键在于增加了可反映插值点与样本点方位关系的调和权重系数K，其基本假设是：距插值点近的样本点，对其后方的样本点有遮蔽效应，当两样本点与插值点的连线夹角α＜360°／n（n为插值搜索邻域内的样点个数）时，遮蔽效应存在，当α≥360°／n时，遮蔽效应消失。在AIDW插值过程中，受遮蔽影响的样本点，其插值权重将被削弱，削弱的程度取决于该样点K值的大小（参见2.2.2节）。

按上述假设：图1（a）所示的5个样点在方向上均匀地分布在插值点（中心点）周围，任意两样点与插值点的连线夹角均大于或等于72°（即α≥360°／5），即认为该5个样点间相互不存在遮蔽效应；在图1（c）中，任意两样点与插值点的连线夹角均小于72°，即认为距插值点的近样点，对其后的样点均具有遮蔽效应；在大多情况下，样点在插值点周围的分布应类似图1（b），既不像图1（a）均匀分布，也不像图1（c）集中分布。图1（b）中Z1、Z3对任一样点均无遮蔽，Z2对Z4、Z5有遮蔽，Z4对Z5也有遮蔽。

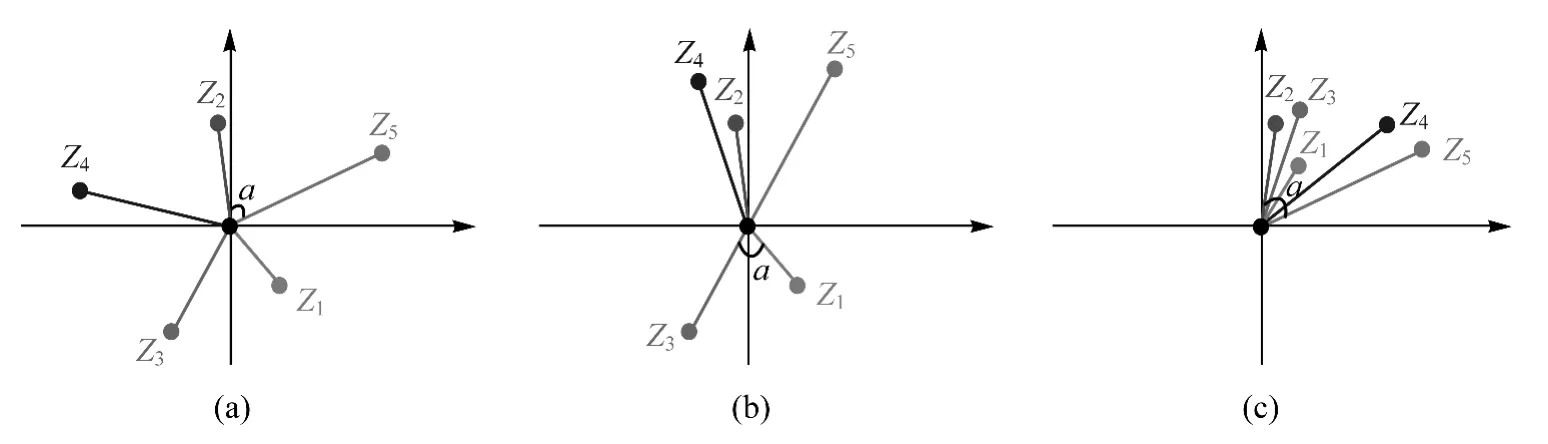
图1 插值搜索邻域中样点散布示例（5个样点）Fig.1 Examples of sample points scattering in searching neighborhood（five points）

2.2.2 算法表达式

将IDW传统的算法思想与本文的基本假设结合，提出了AIDW算法，该算法可被表达为

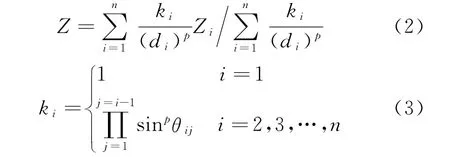
式中，Z、Zi、di、n及p的定义与式（1）相同；i为插值搜索邻域内的样点距插值点远近的排序序号（排列顺序为由近至远）；ki是序号i样点的方位调和权重系数，它表示序号i样点受其他样点遮蔽的综合效应。因序号为1的样点距插值点最近，任何样点都不会对其有遮蔽影响，故设定k1＝1。sinpθij是序号i样点受序号j样点遮蔽程度的计算式

式中，1≤j≤i－1，θij是序号i、j两样点连线与其中线（过插值点）的夹角（锐角或直角）；aij是序号i、j两样点与插值点的连线夹角（图2）。依据AIDW的基本假设，当αij≥360°／n时，序号j样点对序号i样点无遮蔽影响，故规定此时的sinpθij值为1。

2.2.3 算式sinpθ对样点遮蔽效应的表达

图2示例解释了样点Zi所受遮蔽效应与其位置的关系以及sinpθ对这种关系的表达能力。在Zi以固定a角逐渐移近插值点Zo的过程中（图2（a）），θ角和sinpθ值在不断增大，Zj对Zi的遮蔽效应逐步降低；当Zi移动到距插值点的距离等于Zj距插值点距离时（即两样点已无先后，Zj、Zi与插值点构成了等腰三角形），θ角为90°，sinpθ＝1，此时表明Zj已不会对Zi产生遮蔽影响。另一种情况，当Zi保持与插值点的距离不变，但逐渐向Zj背后靠近时（图2（b）），显然样点Zj对Zi的遮蔽效应在逐步增大，这一过程中θ角和sinpθ值也在不断变小；当Zi移动到Zj与插值点连线的正后方，此时θ角变为0°，sinpθ＝0，表明Zj已完全遮蔽了Zi对插值点的影响。

图2 sinpθ随样点位置的变化示例Fig.2 Examples of sinpθvalue changing with sample point moving

若将样点Zi的变化位置看作是其他样点的分布，则图2解释了插值样点在两种特例分布下θ和sinpθ的极端变化情况。即两样点与插值点的距离趋近于等同，θ→90°，sinpθ→1；某样点位置趋向于另一样点（与插值点连线）正后方，θ→0°，sinpθ→0。通常情况下，有遮蔽效应的两样点，它们的θ角多介于0°～90°，sinpθ值多介于0～1。

2.3 AIDW的特点分析

由于AIDW综合考虑了样点距离和样点方位对插值点的共同影响，因而其插值过程（图3）和插值结果（图4）较IDW更趋于合理。从图3（a）中可看出，插值样点在各向上的分布，较难满足样点均匀布局这一IDW插值基本假设，此种情况下IDW的插值可靠性难以保证。AIDW插值考虑了样点间的方位影响，通过计算各样点间的遮蔽效应，削减受遮蔽样点的插值权重。按AIDW算法，在图3（b）中因Z1对Z6、Z3对Z7和Z8、Z4对Z7有遮蔽影响，这些受遮蔽样点的插值权重被削减，Z10、Z11、Z12分别被Z4、Z3、Z7完全遮蔽，它们的插值权重降至为0。依照式（2）和式（3），最终插值点估算值的计算式为

式中，Z为插值点（中心点）估算值；Z1—Z9为样点观测值；d1—d9为样点与插值点的欧氏距离；p是幂指数；θ角如图3（b）所示。由此看来，从某种意义上可以说AIDW算法可使插值样点的分布在各向上更趋于均匀。

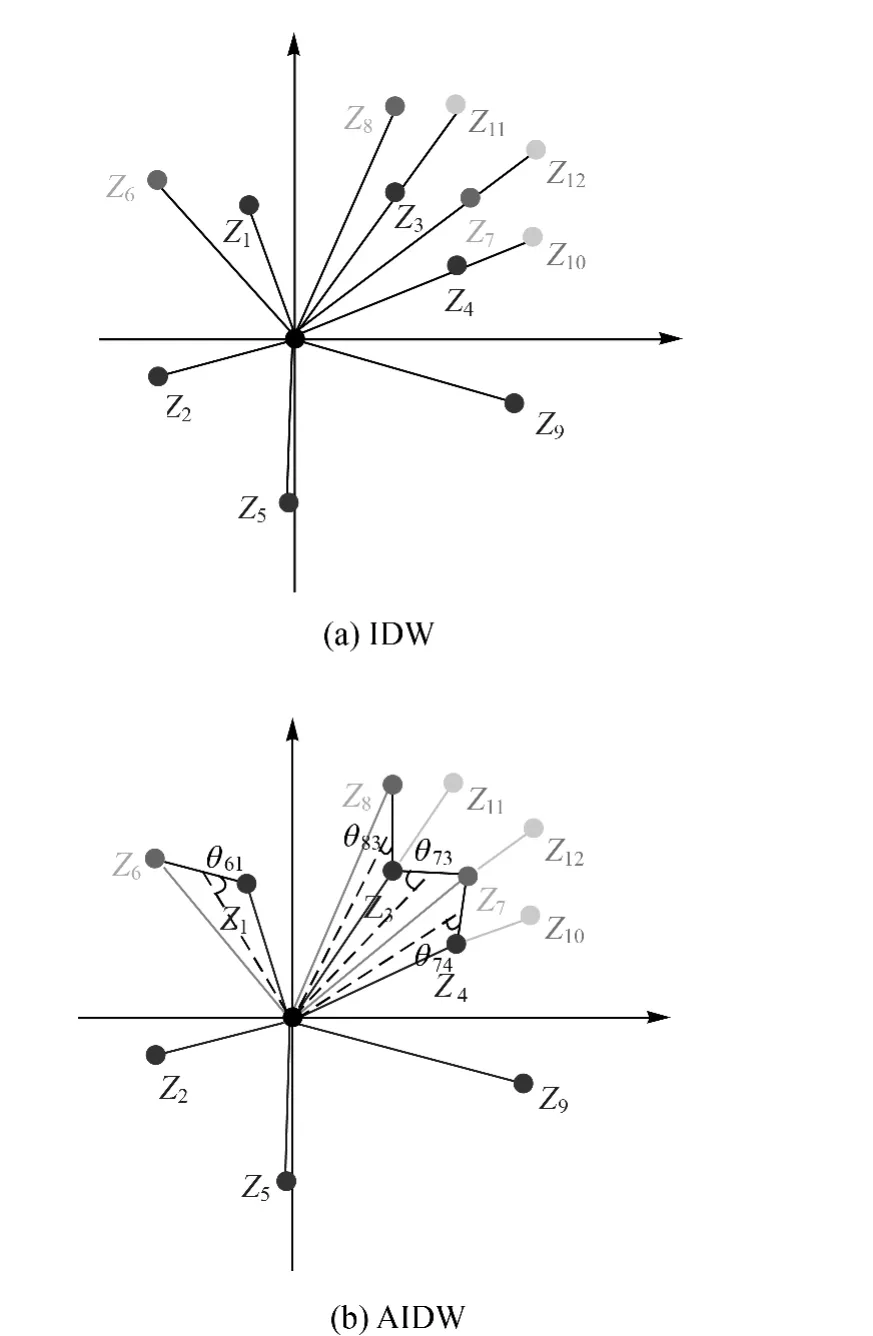
图3 IDW和AIDW两种插值的样点处理方式Fig.3 Treating mode of sample points of the IDW and AIDW interpolations

为了便于理解AIDW和IDW两种插值在等值线绘制中的各自表现，本文用一个简单特例对其加以表述。在图4中紫色样点与插值点（黑色点）呈等距离分布，距离为1；浅橙色样点与插值点也呈等距离分布，距离为2，且浅橙色样点位于插值点与紫色样点连线的正后方，各样点的观测值如图4所示。按IDW算法（p＝1），插值点的估算值为50；按AIDW（p＝1）算法，插值点的估算值为20（浅橙色样点完全被遮蔽，仅需考虑紫色样点插值权重）。从样点数据值的分布可看出（图4，等值线为30和40），很大程度上AIDW要比IDW的插值结果更趋于合理。IDW算法使低值点中出现了高值，其等值线绘制也就增大了“牛眼”的出现几率；而AIDW插值结果与临近数据值接近，很好地避免了“牛眼”现象（图4（b））。有关AIDW和IDW的插值误差及其等值线绘制的实例对比分析，参见第4节。

3 AIDW插值程序设计

AIDW的插值程序可分为插值前准备和插值计算两个过程。插值前准备主要是用于搜索合适的插值样点，并为下一步的插值计算提供di和fij值；插值计算过程主要是求算反映样点遮蔽程度的sinpθij值，并结合di、Zi值求算插值点的Z值（图5）。插值搜索邻域的大小以格点数（k×k）表示，m是搜索邻域内的样点数，n是插值所需的样点数，d、f分别为样点与插值点的欧氏距离和两样点间的欧氏距离，i、j、u、v均为插值样点的序号（i＝1，2，…，n；有1≤j≤i－1、u＜j、i＜v≤n），aij、θij、Zi与式（4）中的定义相同。

sinpθij的求算涉及到两次运用三角余弦定理，一次是判别条件cosαij的求算，另一次是cosθij的求算。为减少程序运算过程，若插值搜索邻域固定样点数的设定大于3个（即n＞3），则两样点是否存在遮蔽的判别条件，程序直接使用cosαij与cos（360°／n）对比，而不使用αij角度与360°／n对比，以便去除对αij角度的求解。另一方面，当出现某样点i被另一样点j完全遮蔽（即cosαij＝1）时，该样点i与其他样点的遮蔽效应，程序采取了判别赋值方式。因已有sinpθij＝0，故i样点与其他样点的遮蔽关系可不再考虑，方便起见可直接赋值sinpθui＝1和sinpθiv＝1（u＜j、i＜v≤n），这种判别赋值方式亦省去一些不必要的sinpθ求算。

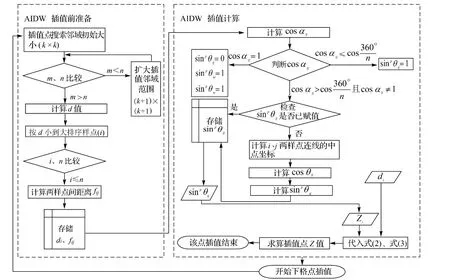
图5 AIDW的插值程序设计流程（n＞3）Fig.5 Flow chart of the AIDW interpolation program（n＞3）

4 AIDW空间插值实例分析

本文对浙江省69个气象台站的某年降水量观测数据，分别利用IDW和AIDW插值算法进行空间插值，进而绘制降水量等值线图。插值实例中，IDW和AIDW算法的p取值为2，插值搜索邻域的固定样点数为5，插值范围为浙江全省，插值空间分辨率即格点大小设置为1km×1km。IDW插值及等值线绘制由ArcGIS软件的ArcMap 9.3完成，AIDW插值和等值线绘制由文中的插值程序及文献［27—28］中的等值线绘制方式完成。

浙江省年降水量IDW和AIDW两种空间插值的误差分析见表1。AIDW插值的平均误差（ME）、平均绝对误差（MAE）、平均相对误差（MRE）以及均方根误差（RMSE），均小于IDW插值方式，尤其是ME和RMSE这两种误差更是明显低于IDW方式，这表明了AIDW相比于IDW，其获得的空间插值结果更趋于合理。

表1 IDW和AIDW空间插值交叉验证的误差分析Tab.1 Errors analysis of cross validation of the IDW and AIDW interpolation

从图6可看出（等值线基值为1000mm雨量，间隔为50mm雨量）：IDW和AIDW两者的等值线图总体分布趋势基本一致（图6（a）），但在局部区域却存在显著差异。区域放大图显示：在浙西开化、浙西北安吉和长兴、浙东南温岭、乐清、温州、瑞安及平阳等区，IDW绘图中出现的同心圆或孤立圆现象（图6（b）），在 AIDW 绘图中（图6（c））得以消除。

图4 IDW和AIDW插值方式的等值线绘制特例Fig.4 Typical examples of contour plotting for the IDW and AIDW interpolation methods

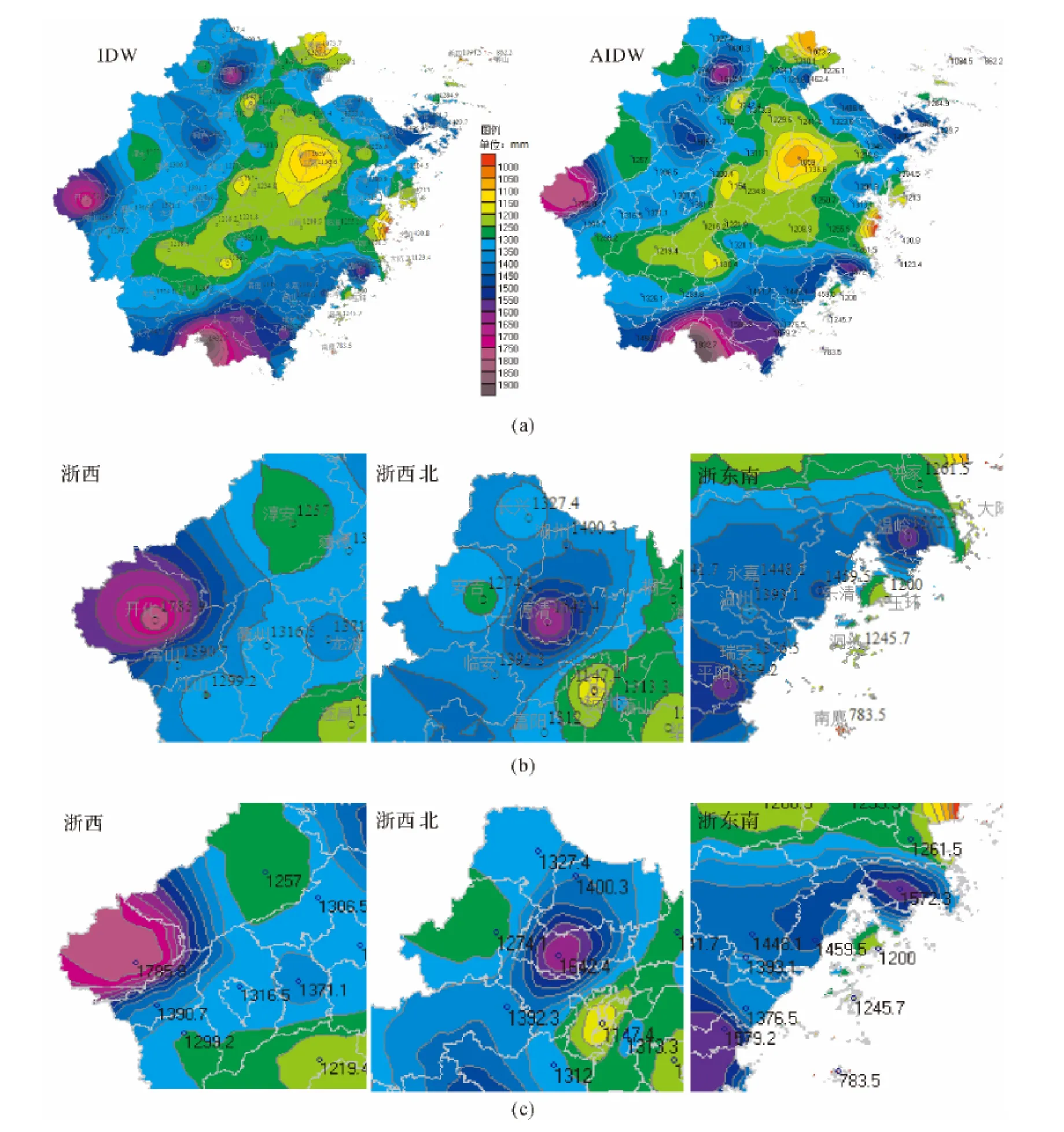
图6 IDW和AIDW插值方式的等值线绘制实例对比Fig.6 Comparison of contour plotting cases of the IDW and AIDW interpolation methods

在浙西开化区，随插值点距开化站（高雨量站）的距离变远，IDW插值的开化站权重会逐渐减小，而常山、江山、衢州和淳安等低雨量站的权重相应增加，故越远离开化站，其降水插值结果越小，从而在开化站周围形成了同心圆等值线（图6（b））。在 AIDW 插值过程中，由于考虑了站点方位遮蔽效应，当对开化站左侧区域插值时，开化站对周围其他站产生了不同程度的遮蔽，且其他站之间也存在遮蔽，由此常山、江山、衢州、淳安等低雨量站的权重被大幅削减，故开化站左侧区的插值未被低雨量站越拉越低，从而避免了同心圆等值线出现（图6（c））。与开化情况相类似的还有浙西北的安吉和浙东南的温岭。在浙西北的长兴区，IDW的等值线图中有一个孤立圆（图6（b）），这是因为湖州和德清两个高雨量站的存在，使得长兴站周围的插值，随距长兴站越远，其插值结果越高，由此等值线绘制也不得不形成一个孤立圆区；而在AIDW插值过程中，当对长兴站左侧区插值时，湖州和德清两个高雨量站因受长兴站的遮蔽以及湖州、安吉两站对德清站的遮蔽，湖州和德清两站的插值权重（尤其是德清站）明显被减小，因此长兴站左侧区的插值结果未被明显拉高，等值线绘制时此区也就与其他区域合并在了一起，并未出现孤立圆现象（图6（c））。与长兴情况相类似的还有浙西南乐清、温州、瑞安及平阳等区。

值得注意的是：AIDW插值算法并未消除IDW绘图中浙西龙游的孤立圆以及浙西北德清和杭州的同心圆现象（如图6（b）和图6（c））。仔细查看可发现，这些站周围的各站点几乎呈均匀布局（上下左右各1个），并不像开化和长兴那样集中于一侧，这也意味着AIDW插值算法即可保留IDW插值思想，又可减小样点分布不均IDW的插值缺陷。简而言之，AIDW相对于IDW，其插值结果更趋于合理，等值线绘制也更接近于人工作业，如开化、安吉、长兴、温岭、乐清、温州、瑞安及平阳等区的等值线走向判识。

5 结 论

AIDW算法依据样点与插值点的连线夹角a判别样点间是否有遮蔽效应，采用两样点连线与其中线（过插值点）夹角的sinpθ值表征样点受遮蔽程度，以方位权重系数调和距离权重，插值过程考虑样点距离和样点方位共同影响，其空间插值结果更趋于合理。基于AIDW空间插值曲面的等值线绘制，可有效减少IDW等值线绘制中孤立圆和同心圆的出现几率，使等值线绘图更具科学美观性。

因AIDW算法涉及cosα和cosθ值求算，故其空间插值运算速度较IDW插值略慢。在浙江省69气象站点的年降水量空间插值实例中，AIDW和IDW插值运算时间均不足1s，但当插值的空间分辨率由1km×1km提高到500m×500m，插值搜索邻域固定样点数设为15个时，浙江全省的AIDW插值运算时间为11s，而IDW插值运算时间为6s。随插值格点总数以及插值搜索邻域固定样点数的增加，AIDW插值运算速度会略慢于IDW插值。

［1］ LONGLEY P A，GOODCHILD M F，MAGUIRE D J，et al.Geographical Information Systems：Principles， Techniques，Management and Applications［M］.New York：Wiley，1999：481－492.

［2］ HENGL T A.Practical Guide to Geostatistical Mapping of Environmental Variables［M］.Ispra：Official Publications of the European Communities，2007：11－24.

［3］ LIU Jianjun，CHEN Jun，WANG Donghua，et al.The Study of Description and Application of Contour Adjacency Relationship［J］.Acta Geodaetica et Cartographica Sinica，2004，33（2）：174－178.（刘建军，陈军，王东华，等.等高线邻接关系的表达及应用研究［J］.测绘学报，2004，33（2）：174－178.）

［4］ YOU Shucheng，YAN Tailai.A Study on Artificial Neural Network Based Surface Interpolation［J］.Acta Geodaetica et Cartographica Sinica，2000，29（2）：30－34.（尤淑撑，严泰来.基于人工神经网络面插值的方法研究［J］.测绘学报，2000，29（2）：30－34.）

［5］ SHI Wenjiao，YUE Tianxiang，SHI Xiaoli.Research Progress in Soil Property Interpolators and Their Accuracy［J］.Journal of Natural Resources，2012，27（1）：163－175.（史文娇，岳天祥，石晓丽.土壤连续属性空间插值方法及其精度的研究进展［J］.自然资源学报，2012，27（1）：163－175.）

［6］ LU G Y，WONG D W.An Adaptive Inverse Distance Weighting Spatial Interpolation Technique［J］.Computer and Geoscience，2008，34：1044－1055.

［7］ DENG Xiaobin.Comparison between Two Space Interpolation Methods Based on ArcGIS［J］.Geospatial Information，2008，6（6）：85－87.（邓晓斌.基于 ArcGIS两种空间插值方法的比较［J］.地理空间信息，2008，6（6）：85－87.）

［8］ KNOTTERS M，BRUS D J，VOSHAAR J H O.A Comparison of Kriging，Co－Kriging and Kriging Combined with Regression for Spatial Interpolation of Horizon Depth with Censored Observations［J］. Geoderma，1995，67（3）：227－246.

［9］ NIU Wenjie.Comparison of Theory and Application between Thin Plate Spline and Universal Kriging［J］.Journal of Engineering Graphics，2010，4：123－129.（牛文杰.薄板样条法和泛克里金法在理论和应用方面的比较［J］.工程图学学报，2010，4：123－129.）

［10］ WANG Jingxin.Research on Spline Interpolation Poisedness and Interpolation Approach Problems［D］.Dalian：Dalian University of Technology，2004.（王晶昕.样条插值适定性与插值逼近问题研究［D］.大连：大连理工大学，2004.）

［11］ TANG Bo，TONG Ling，KANG Shaozhong.Effects of Spatial Station Density and Interpolation Methods on Accuracy of Reference Crop Evapotranspiration［J］.Transactions of the Chinese Society of Agricultural Engineering，2013，29（13）：60－66.（汤博，佟玲，康绍忠.站点密度及插值方法对ET0空间插值精度的影响［J］.农业工程学报，2013，29（13）：60－66.）

［12］ LI Xin，CHENG Guodong，LU Ling.Comparison of Spatial Interpolation Methods［J］.Advance in Earth Sciences，2000，15（3）：260－265.（李新，程国栋，卢玲.空间内插方法比较［J］.地球科学进展，2000，15（3）：260－265.）

［13］ LIU Jinsong，CHEN Hui，YANG Binyun.Comparison of Interpolation Methods on Annual Mean Precipitation in Hebei Province［J］.Acta Ecologica Sinica，2009，29（7）：3493－3500.（刘劲松，陈辉，杨彬云.河北省年均降水量插值方法比较［J］.生态学报，2009，29（7）：3493－3500.）

［14］ ZHANG Meihua，LIANG Wenkang.An Improved Method for Contouring on Network of Triangles［J］.Journal of Computer－Aided Design and Computer Graphics，1997，9（3）：213－217.（张梅华，梁文康.一个三角形网格上等值线图的绘制算法［J］.计算机辅助设计与图形学学报，1997，9（3）：213－217.）

［15］ HU Jinxing，MA Zhaoting，WU Huanping，et al.Massive Data Delaunay Triangulation Based on Grid Partition Method［J］.Acta Geodaetica et Cartographica Sinica，2004，33（2）：163－167.（胡金星，马照亭，吴焕萍，等.基于格网划分的海量数据Delaunay三角剖分［J］.测绘学报，2004，33（2）：163－167.）

［16］ ZHANG Yao，FAN Hong，HUANG Wang.The Method of Generating Contour Tree Based on Contour Delaunay Triangulation［J］. Acta Geodaetica et Cartographica Sinica，2012，43（3）：461－467.（张尧，樊红，黄旺.基于Delaunay三角网的等高线树生成方法［J］.测绘学报，2012，43（3）：461－467.）

［17］ DALE Z，CLAIRE P，AMY R，et al.An Experimental Comparison of Ordinary and Universal Kriging and Inverse Distance Weighting［J］.Mathematical Geology，1999，31（4）：375－390.

［18］ AZPURUA M，RAMOS K D.A Comparison of Spatial Interpolation Methods for Estimation of Average Electromagnetic Field Magnitude［J］.Progress In Electromagnetics Research M，2010，14：135－145.

［19］ CAROL A G，RICHARD B F，GARY W H，et al.Comparison of Kriging and Inverse Distance Methods for Mapping Soil Parameters［J］.Soil Science Society of A－merica Journal，1996，60（4）：1237－1247.

［20］ ZHU Huiyi，LIU Shulin，JIA Shaofeng.Problems of the Spatial Interpolation of Physical Geographical Elements［J］.Geographical Research，2004，23（4）：425－432.（朱会义，刘述林，贾绍凤.自然地理要素空间插值的几个问题［J］.地理研究，2004，23（4）：425－432.）

［21］ FENG Zhiming，YANG Yanzhao，DING Xiaoqiang，et al.Optimization of the Spatial Interpolation Methods for Climate Resources［J］.Geographical Research，2004，23（3）：357－364.（封志明，杨艳昭，丁晓强，等.气象要素空间插值方法优化［J］.地理研究，2004，23（3）：357－364.）

［22］ NUSRET D，DUG S.Applying the Inverse Distance Weighting and Kriging Methods of the Spatial Interpolation on the Mapping the Annual Precipitation in Bosnis and Rzegovina［C］∥Proceedings of International Congress on Environmental Modelling and Software.Leipzig：［s.n.］，2012.

［23］ SHEPARD D.A Two－dimensional Interpolation Function for Irregularly－Spaced Data［C］∥ Proceedings of the 1968 ACM National Conference.New York：ACM Press，1968：517－524.

［24］ WATSON D F，PHILIP G M.A Refinement of Inverse Distance Weighted Interpolation［J］. Geoprocessing，1985，2：315－327.

［25］ ZENG Hongwei，LI Lijuan，ZHANG Yongxuan，et al.Study on Spatial Interpolation of Precipitation with Large Scale Samples：A Case Study on 2009’s Precipitation of China［J］.Progress in Geography，2011，30（7）：811－818.（曾红伟，李丽娟，张永萱，等.大样本降水空间插值研究：以2009年中国年降水为例［J］.地理科学进展，2011，30（7）：811－818.）

［26］ HUSAR R B，FALKE S R.Uncertainty in the Spatial Interpolation of PM10Monitoring Data in Southern California［J／OL］.［1996－04－05］.http：∥capita.wustl.edu／CAPITA／capitareports／CAInterp／CAINTERP.doc.

［27］ XIE Shunping，TIAN Desen.To Improve Tracing Isopleth by Route Grid Method［J］.Acta Geodaetica et Cartographica Sinica，1995，24（1）：52－56.（谢顺平，田德森.完善等值线追踪的路径栅格法［J］.测绘学报，1995，24（1）：52－56.）

［28］ WANG Yu，ZHU Changqing，SHI Wenzhong.Application of B Spline and Smoothing Spline on Interpolating the DEM Based on Rectangular Grid［J］.Acta Geodaetica et Cartographica Sinica，2000，29（3）：240－244.（王昱，朱长青，史文中.B样条与磨光样条在基于矩形格网的DEM内插中 的应用 ［J］.测绘学报，2000，29（3）：240－244.）